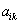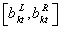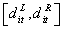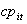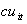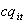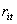1. Introduction

The objective of the production planning problem is the maximization of the revenue. For solving it, the demand and resource levels are assumed to be fixed and given. But a production planning problem exists because there are limited production resources that cannot be stored from period to period. Also the planning problem starts with a specification of customer demand that is to be met by the production plan. In most contexts, future demand is partially known. So one relies on a forecast for the future demand but the forecast is inaccurate. This leads to that demand that cannot be met in a period is lost, thus reducing revenue. So a production planning problem to maximize revenues net of the production, inventory and lost sales costs is suggested by Stephen C. Graves[1]. For solving it, the coefficients of the objective function, the inequalities and the equalities constraints are assumed to be known numbers.

In real world, the data are imprecise that is the data can be represented as uncertainty. In the real world there are many forms of uncertainty that affect production processes. Uncertainty always exits in practical engineering problems. In order to deal with the uncertain optimization problems, fuzzy and stochastic approaches are commonly used to describe the imprecise characteristics. In stochastic programming[20] the uncertain coefficients are regarded as random variables and their probability distributions are assumed to be known. In fuzzy programming[21] the constraints and objective function are viewed as fuzzy sets and their membership functions also need to be known. In these two kinds of approaches, the membership functions and probability distributions play important roles. It is sometimes difficult to specify an appropriate membership function or accurate probability distribution in an uncertain environment[22]. The interval analysis method was developed to model the uncertainty in uncertain optimization problems, in which the bounds of the uncertain coefficients are only required, not necessarily knowing the probability distributions or membership functions. So for the first time, we will deal the production planning problem with interval data as uncertainty in both of the objective function and constraints.

2. Review Literature

Production planning is a complicated task which requires cooperation among multiple functional units in an organization. For solving the problem of production planning, powerful optimization models have been constructed by means of the formulation of mathematical programming. We refer to[1,7] for an overview of optimization techniques in this field.

Galbraith[3] defines uncertainty as the difference between the amount of information required to perform a task and the amount of information already possessed. we refer to[13] for applying a fuzzy linear programming method for solving model related to aggregate production planning problem with multiple objectives. also we refer to[19] for applying a stochastic linear programming method for solving model related to supply chain planning with bi-level linear multiple objective programming. As the recent contribution for the problem of concern can be viewed as follows:

R. Svend[23] discusses how the linear programming model can be used as the basis for a company’s operational planning, in practice. F. G. Juan Carlos et al.[24] developed a new model for production planning using fuzzy sets in order to use classical mathematical programming techniques to reach an optimal solution over a multiple criteria context.

Production planning problem that involve the lost of future demand have been investigated by Stephen C. Graves[1]. This problem deals with precise coefficients in both of objective function, the inequalities and the equalities constraints. While the data in the real world are imprecise then the input data can be represented as uncertainty.

In our work, we develop a new planning problem to minimize the lost demands and thus maximize revenues. For the first time, we construct the production planning problem with interval numbers as uncertainty in both of the objective function and constraints. After that we will treat the uncertain of objective function and constraints. In section 5, parametric study for the treatment problem is introduced. Finally, for illustration, a production planning example is given, where the integer programming optimal solution is determined using the WinQSB software package.

3. Solution Algorithm

In this sub section, we describe a solution algorithm for solving problem (1)-(14).

Algorithm steps:

Step 1: Construct the production planning problem with interval numbers in both of the objective function and constraints as in (1)-(14).

Step 2: Read the interval values of 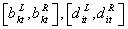and the values of 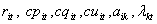where i = 1,2,3, t = 1,2, k = 1,2,3.

Step 3: Convert the problem (1)-(14) to the deterministic form (45)-(64).

Step 4: solve the problem by WinQSB software package.

Step 5: Stop.

4. Methodology Adopted

In this study, production related data of Al- Araby firm for electric sets in Egypt was collected. Data was collected, classified and analyzed statistically. Linear programming model was formulated based on the outcomes of the analyzed data. The data were collected through the use of questionnaires and oral interview among employees in the firm. The data that were collected include the following:

The firm is planning for production of three items: refrigerators, ovens and washing machines. The manufacturer of each item requires three resources. These resources are number of workers, over time and varying inventory. There are two time periods for production. The length of each time period is six months. The amount of the three resources required of production of the three items is illustrated in table (1). The amounts of available resource and demand for each item are represented by interval numbers as illustrated in tables (2) and (3) respectively. The cost of production of the three items in a given two time periods is illustrated in table (4). The unit cost of unmet demand of the three items in a given two time periods is illustrated in table (5). The unit inventory holding costs of the three items in a given two time periods is illustrated in table (6). The unit revenue for each item in each time period is illustrated in table (7).

Table 1. Required resources of production Total required resources Production requirements Refrigerators Ovens washing machines Number of workers 8 6 5 Overtime 4 3 5 Varying inventory 30 50 60

Table 2. Amounts of available resources Total available resources Production requirements Time period 1 Time period 2 Number of workers (60,130) (70,100) Overtime (500,700) (500,700) Varying inventory (60,80) (80,90)

Table 3. Amounts of demand resources Production requirements The demand Time period 1 Time period 2 Refrigerators (5000,7000) (7000,9000) Ovens (5000,7000) (7000,9000) washing machines (5000,7000) (7000,9000)

Table 4. Production cost of three items Production requirements Cost of production Time period 1 Time period 2 Refrigerators 1500 1550 Ovens 1000 1050 washing machines 1500 1550

Table 5. Unit cost of unmet demand Production requirements Cost of unmet demand Time period 1 Time period 2 Refrigerators 100 120 Ovens 70 70 washing machines 90 100

Table 6. Unit inventory holding costs Production requirements Cost of inventory holding Time period 1 Time period 2 Refrigerators 30 30 Ovens 20 15 washing machines 25 20

Table 7. unit revenue of each item in each period Production requirements The revenue Time period 1 Time period 2 Refrigerators 3000 3500 Ovens 2000 2500 washing machines 3000 3500

The decision variables are as follows:

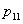= the amount of production of refrigerators during time period 1.

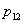= the amount of production of refrigerators during time period 2.

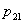= the amount of production of ovens during time period 1.

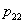= the amount of production of ovens during time period 2.

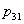= the amount of production of washing machines during time period 1.

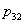= the amount of production of washing machines during time period 2.

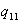= the amount of inventory of refrigerators at end of time period 1.

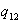= the amount of inventory of refrigerators at end of time period 2.

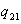= the amount of inventory of ovens at end of time period 1.

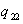= the amount of inventory of ovens at end of time period 2.

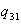= the amount of inventory of washing machines at end of time period 1.

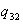= the amount of inventory of washing machines at end of time period 2.

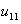= the amount of unmet demand of refrigerators during time period 1.

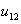= the amount of unmet demand of refrigerators during time period 2.

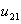= the amount of unmet demand of ovens during time period 1.

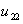= the amount of unmet demand of ovens during time period 2.

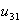= the amount of unmet demand of washing machines during time period 1.

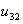= the amount of unmet demand of washing machines during time period 2.

With these variables, it is possible to formulate the production planning problem that maximizes revenues net of the production inventory and lost sales cost with interval numbers as follows:

Maximize Z

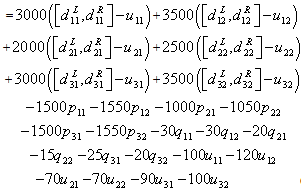(1)

subject to

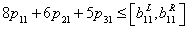(2)

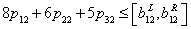(3)

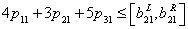(4)

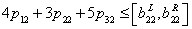(5)

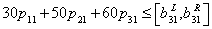(6)

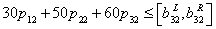(7)

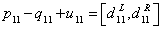(8)

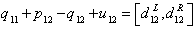(9)

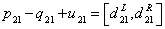(10)

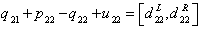(11)

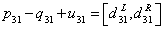(12)

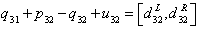(13)

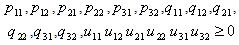(14)

5. The Optimization Approach

Based on the proposed approach of Jiang[8] for treating interval number, we will treat the uncertainty of model (1)-(14) as follows:First: Treatment of the uncertain objective function

Let

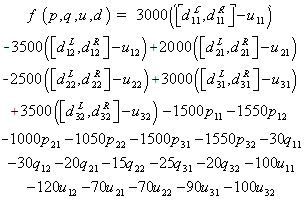(15)

in interval mathematics, The uncertain objective function (1) can be transformed into two objective optimization problems as follows:

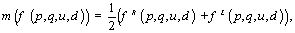(16)

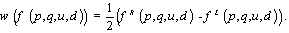(17)

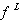where m is called the midpoint value, w is called the radius of interval number and the two functions and 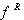are given as follows:

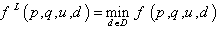and 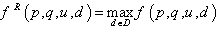where .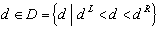

Then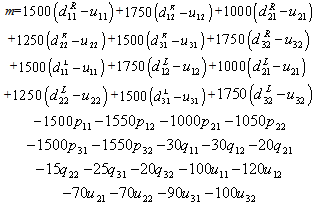

(18)

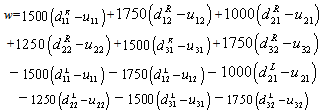(19)

Second: Treatment of the uncertain constraints

The possibility degree of interval number represents certain degree that one interval number is larger or smaller than another. The set of inequality constraints (2)-(7) can be written as

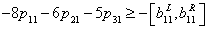(20)

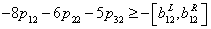(21)

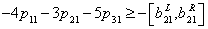(22)

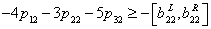(23)

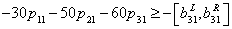(24)

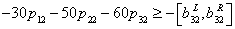(25)

As in interval linear programming[18], the possibility degree of the constraints (20) can be written as follows

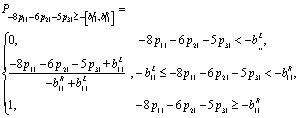(26)

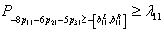is the possibility degree of the constraint (20). 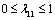is a predetermined possibility degree level. the other inequality constraints are treated in the same way. Then the constraints (2) - (7) can be written as

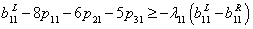(27)

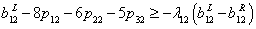(28)

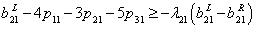(29)

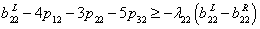(30)

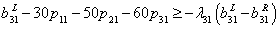(31)

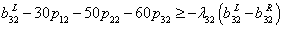(32)

The equality constraints (8)-(13) can be treated as follows

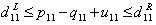that can be written as

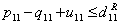(33)

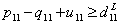(34)

the other equality constraints are treated in the same way. Then the constraints (9)-(13) can be written as

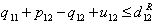(35)

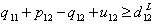(36)

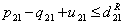(37)

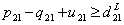(38)

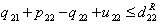(39)

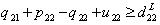(40)

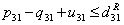(41)

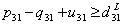(42)

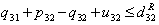(43)

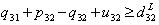(44)

6. The Deterministic form of Problem (1)–(14)

The linear combination method[2,5,6] is adopted with the multi objective optimization. In multi objective optimization, applying the linear combination method to integrate the objective function is relatively easy provided that the preferences of the objective functions are available. Then two objective function (18), (19) can be written in the form of only one objective function.

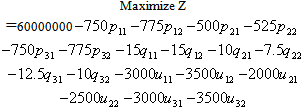(45)

subject to

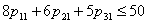(46)

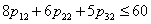(47)

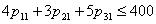(48)

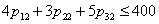(49)

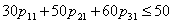(50)

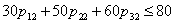(51)

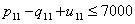(52)

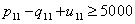(53)

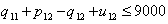(54)

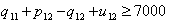(55)

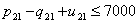(56)

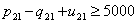(57)

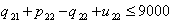(58)

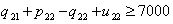(59)

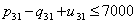(60)

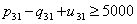(61)

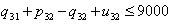(62)

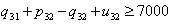(63)

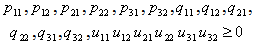(64)

By using WinQSB package for solving this problem, we get the optimal solution as follows:

Net revenue Z=$2,951,510

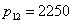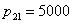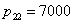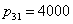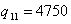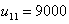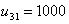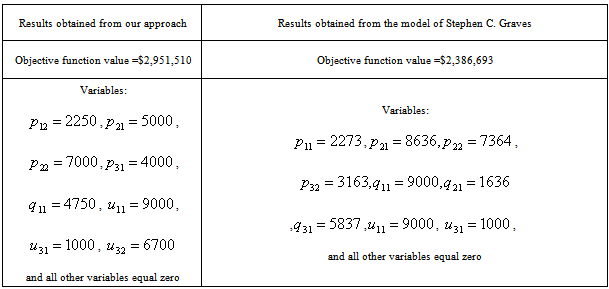
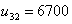,, , , , , , and all other variables equal zero.

Table (8) shows the comparison between the results of our approach which is based on uncertainty case and one's of Stephen C. Graves approach[1] which is based on the deterministic case.

It is clear that the results obtained from our approach are better than the results obtained by Stephen C. Graves especially for the objective function value.

Table 8. comparison results between our approach and one’s Stephen C. Graves[1]

7. Conclusions

In this paper, However, as a point for future research, a comparison study is needed between the interval and fuzzy programming to tackle the production planning problem, where each of fuzzy programming and interval programming are two forms of uncertainty. This point for future research is to determine which of interval and fuzzy programming is more suitable for problem of concern.