-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Operational Research
2012; 2(4): 31-44
doi: 10.5923/j.ajor.20120204.02
A Hybrid Ant Colony System for Partially Dynamic Vehicle Routing Problem
Hannaneh Rashidi 1, Reza Zanjirani Farahani 2
1Young Researchers Club, Karaj Branch, Islamic Azad University, Alborz, Iran
2Department of Informatics and Operations Management, Kingston Business School, Kingston University, London, UK
Correspondence to: Hannaneh Rashidi , Young Researchers Club, Karaj Branch, Islamic Azad University, Alborz, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The constraints on responding time involved with dynamic vehicle routing problem (DVRP) require a compromise between distance and time in order to obtain the best solutions as fast as possible, so the flow time and the number of lost customers have gotten the mean to DVRP. Here, we propose a hybrid ant colony system (ACS) initially applied to design a static version of vehicle routing problem (VRP). Then, stochastic information of customers is used to be considered in the partially dynamic version of VRP. Our approach uses some heuristics to reconstruct routes and update pheromone. This approach for solving DVRP with the proper combination of parameters is compared with an insertion heuristic on the benchmark problems of Solomon's instances. The results show that our approach acts well in comparing some heuristic methods.
Keywords: Dynamic Vehicle Routing Problem, Ant Colony System, Neighbourhood Search
Article Outline
1. Introduction
- Vehicles routing and scheduling through a set of required services, could be counted as a key element in many distribution systems both in the private and public sectors. In vehicle routing problem (VRP), a fleet of vehicles supplies a set of geographically dispersed customers to construct optimal routes with a minimal cost regarding distance, time, and the number of vehicles. Each vehicle goes through a tour, and each tour starts from a depot going towards customers to satisfy their demands.If the unknown attributes have been integrated with the constraints of VRP, the system has to incorporate changes and modify the scheduling to an appropriate one. This dynamically responding to requests is termed as dynamic VRP (DVRP), or on-line VRP, which is also well-known as real time VRP (RTVRP); noteworthy these titles are corresponded with the quality and quantity of the responding system’s capability. As it is pointed out in reference[32], DVRP based on the degree of dynamism and objective function can be termed as weakly or moderately or strongly dynamic system. For example, a dial-a-ride problem with the number of immediate requests being quite low, in which requests are booked before the day of the trip, is considered to be a weakly dynamic system ([19],[10],[58],[42]). Repair and mail services are counted as moderately dynamic routing systems ([23],[34]). In moderate systems, there is a need to have reaction to requests as soon as possible but not as fast as emergency cases that are known to be strongly dynamic systems ([24],[7]). Corresponding to the level of dynamism of DVRP, there are different optimizing methodologies such as heuristic and meta-heuristic methods. Our study utilizes the ant colony system (ACS) along with some quick heuristic methods to divert a vehicle away from its current destination to respond new requests.
1.1. The Motivations and Contributions
- This paper has been inspired by the works done by references[23] and[39]. The main difference between our work and their studies is our account for some heuristic methods on ACS along with the scenarios of the DVRP. This is done to adapt the methodology with time restriction in order to find enough good solutions quick. In our method, new requests arriving during a slice time are listed and posted to the next closest time slice. During each time slice, a problem similar to a static VRP, but with vehicles having different capacities and starting locations, is traced. This is a soft time window-based problem, in which requests should be responded dynamically. The future requests are not known, however the demands occur with Poison distribution function whereas the locations of requests are known. Regarding the order of the requests, vehicle are assigned to carry out them, therefore some requests may be postponed. This is the reason that we call it as a partially moderate DVRP.The main contribution of our work is to develop a constructive structure to re-optimize routes for occurred events in the requests list. Although time window vehicle routing problems have been studied extensively, there is not a lot of ACS researched dedicated to solve DVRP (see Table 1). Insertion heuristic, tabu search, local search and genetic algorithm have attracted the most considerations in this field. Among them, the construction structure of ACS is well to solve routing kind problems; however the running time of this algorithm may seem high for DVRP. In this paper, we try to design an efficient ACS with setting appropriate parameters besides initial pheromone and increasing pheromone methodology. Moreover, neighborhood searches help us to reach feasible solutions quick. We prove that applied ACS is a suitable method for the proposed partially moderate DVRP.Regarding the points have been cleared in[28] to have more logical judgments about the quality of the solutions, we make use of an alternative objective function in place of a distance-based objective function. Authors of[28] show the objectives of minimizing the make-span or the latency are inadequate since both will always be infinite. Thus, they consider the objectives of maxima and average flow time, which is the difference between the completion and release time. We use a combined idea of distance and flow time as the objective function.
1.2. The Applications of Model
- The main purpose of our model is to apply for the repair, fuel distribution, courier and mail service systems or other moderate routing problems. Broken car rescue, appliance repair are counted as repair services that are evolved in real time. In the courier and email service systems, there are a limited number of vans going around a specified location to collect parcels in order to consolidate loads. Sometimes, dynamic pick-up requests have to be serviced in a same day. It is noteworthy that our study could be applicable for static version of VRP, too.The application of this problem could be found in considering the realistic property, which is occurring continuously. There are different real problem categorizes that must be solved dynamically regarding time windows constraints. For example[41] applies soft time windows constraint on vehicle scheduling within airport logistic. Dial-a-ride system is another example, which gives transportation service to (handicapped or elderly) people between given origin and destination pairs. This system can be divided into the static model when trips are booked one day in advance ([10],[42]) or the dynamic models handling short notices ([35],[58]).
1.3. The Organization of paper
- The rest of this paper is organized as follows. A review on the literature is presented in Section 2. The definition of the VRP and supposed dynamic strategy are provided in Section 3. The ACS procedure for real time responding to requests is presented in Section 4. Section 5 using Taguchi method takes into account the calibration of parameters and operators. A discussion on numerical results in comparing with other methods is given in Section 6. Lastly, conclusions and future work are presented in Section 7.
2. Literature Review
- VRP falls into the combinatorial optimization and integer programming problem categories, being studied extensively in the past forty years. The research was done in [13] as the first paper on VRP has been followed by a significant number of scholars until the present time. Readers are referred to refernce[16], in which there is a comprehensive taxonomy of classifications and categories contributed by VRP.The disparate structure of the literature of this problem makes it quite difficult to track developments on the subject. This subject covers several theoretical and practical disciplines from algorithm design to traffic management. Actually, VRP's facets encompass a spectrum from stochastic to deterministic areas and from static to dynamic issues. It could be said that time windows structure ([52],[40],[9],[3],[36],[38]), time horizon structure ([35],[10]), and backhauls ([14],[54]) are there general scenario characteristics of VRP.There is a large portion of the literature on static VRP, which may be termed as traditional VRP. In the static VRP, the data such as the locations, load splitting, demand quantities, capacities of vehicles, request time, driving time, waiting time, and service time are known and deterministic ([49],[11],[43],[60],[38]). The complex structure of DVRP for scheduling orders to vehicles and vehicles to routes admits difficulties for finding feasible solutions, and this is the cause for lack of large number of researches in this field. With the enhanced computational capability offered in the 1990s and the enhancement in vehicle tracking, exchange media, and data storage, DVRP has been more common in the literature ([1],[2],[18],[39],[51],[6],[50],[30],[4]). A variety of solution methodologies including heuristics, simulations and exact methods with regard to service strategies, relations between vehicles-customers along with supposing appropriate objective functions, have been developed to encounter DVRP models. Authors of[23] develop a parallel tabu search (TS) to find minimum cost of delay on service for presumed soft time windows. A survey on results obtained on different types of DVRPs can be found in[22]. References[26] and[39] develop different approaches of ant colony algorithm for DVRP. Reference[6] considers a granular local search heuristic for RTVRP. Note that partially dynamic vehicle routing problems may vary greatly in complexity according to the characteristics of dynamism, which have been classified as in[45] and[25].The first DVRP study dates back to reference[44], which surveyed uncertainty in VRP with stochastic flows of vehicles. It could be said that stochastic routing is another attracting subject in VRP literature, in which supposing stochastic nature of events made it more close to real-world problems ([57],[56]).The concept of DVRP and RTVRP encompasses time window constraints on request nodes. Therefore, some DVRP fall under the stochastic vehicle routing problem category too([5],[21],[20],[29],[55],[17],[47]).The DVRP in which stochastic information about future request is known could be called dynamic and stochastic VRPs. In the current paper, we focus on the dynamic frame of VRP, in which routes could be changed regarding time windows. The ACS algorithm is used to solve the partially DVRP with stochastic characteristic of occurring future events with known demands and location.
3. The Dynamic Vehicle Routing Problem
- The VRP can be described as a weighted graph-theoretic problem. Let
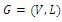 indicates the graph, where
indicates the graph, where 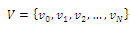 are vertices,
are vertices, 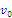 is the central depot, and the other nodes are N customers that have to be served. The arcs connecting vertices are represented with
is the central depot, and the other nodes are N customers that have to be served. The arcs connecting vertices are represented with 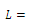
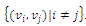 . There is a nonnegative demand
. There is a nonnegative demand 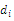 for each node and a nonnegative cost
for each node and a nonnegative cost 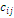 associated with each arc
associated with each arc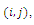 which usually stands for the traveling distance from vertex
which usually stands for the traveling distance from vertex 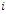 to vertex j . Since
to vertex j . Since 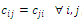 , so the problem is called symmetric. In several practical cases, the triangular inequality holds, that is
, so the problem is called symmetric. In several practical cases, the triangular inequality holds, that is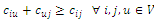 . The objective is to find a collection of K simple circuits with minimum cost satisfying the following constraints:(1) Each circuit visits the depot.(2) Each vertex is visited by exactly one circuit.(3) The sum of the vertices’ demands visited by a circuit does not exceed the vehicle capacity.Here, we explain how motions can be evaluated in time window constraints. The static mode can design routes by applying supposed ACS, but the key discussion is on dynamic routing. We survey the strategy aimed at discarding moves which are not most likely to yield any improvement. First of all, some descriptions about the basics of DVRP are given.
. The objective is to find a collection of K simple circuits with minimum cost satisfying the following constraints:(1) Each circuit visits the depot.(2) Each vertex is visited by exactly one circuit.(3) The sum of the vertices’ demands visited by a circuit does not exceed the vehicle capacity.Here, we explain how motions can be evaluated in time window constraints. The static mode can design routes by applying supposed ACS, but the key discussion is on dynamic routing. We survey the strategy aimed at discarding moves which are not most likely to yield any improvement. First of all, some descriptions about the basics of DVRP are given.3.1. The DVRP Definitions
- We consider the general case that some requests (of the pick up or delivery) could arrive randomly, just like courier distribution systems. Travel times are updated based on real time information; however, travel distances are kept constant in all experiments. All vehicles are assumed to be similar and there are capacity constraints for all of them, and the pre-defined number of vehicles is assumed to be sufficient to serve the average of the requests. There is no concentration of vehicles in a small area and the route loads are balanced. Moreover, when vehicles leave the depot, they do not have to go back to it, unless there is not enough capacity for servicing or when all the customers have been serviced. Notably, no service would be canceled even if delays are faced.In the version of DVRP considered having time windows, each customer should be served within the earliest and latest service times giving as an interval
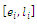 . The demands for servicing new customers are generated at the nodes of the network according to a Poisson process. The travel times among nodes are known and deterministic, and each vehicle spends a known service time for each new coming customer. In this condition, part of the input is revealed to the dispatcher, while servicing the static requests. Given this, it is impossible for optimal routes to be produced in advance. At the best, what can be produced is to determine what action should be taken as a function of the state of the system. Figure 1 shows an example of DVRP considered by time windows. The pre-planned customers and dynamic requests are depicted by grey and white nodes, respectively. The pre-planned routes are represented by solid lines. The thick arcs indicate the current positions of vehicles at the time the immediate requests are received. The new customers have to be inserted into the already planned routes with a minimal delay. Because of the time window constraints, some new requests, like
. The demands for servicing new customers are generated at the nodes of the network according to a Poisson process. The travel times among nodes are known and deterministic, and each vehicle spends a known service time for each new coming customer. In this condition, part of the input is revealed to the dispatcher, while servicing the static requests. Given this, it is impossible for optimal routes to be produced in advance. At the best, what can be produced is to determine what action should be taken as a function of the state of the system. Figure 1 shows an example of DVRP considered by time windows. The pre-planned customers and dynamic requests are depicted by grey and white nodes, respectively. The pre-planned routes are represented by solid lines. The thick arcs indicate the current positions of vehicles at the time the immediate requests are received. The new customers have to be inserted into the already planned routes with a minimal delay. Because of the time window constraints, some new requests, like 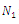 might not be satisfied. Since our approach is not to reject requests, unsatisfied orders should be saved to be considered in the next work slices.
might not be satisfied. Since our approach is not to reject requests, unsatisfied orders should be saved to be considered in the next work slices.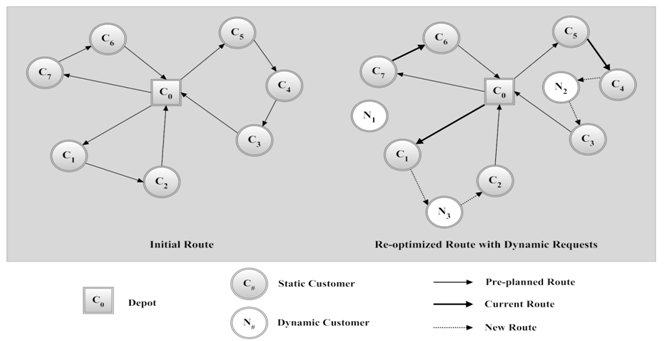 | Figure 1. An example of DVRP with seven pre-planned customers and three immediate requests |
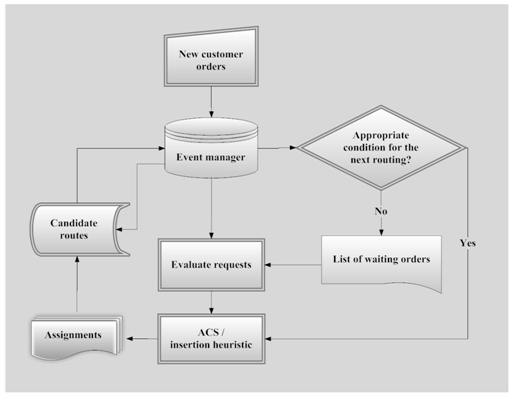 | Figure 2. An architecture of DVRP algorithm |
|
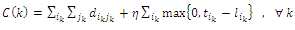 | (1) |
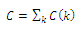 | (2) |
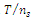 , where T is the length of the working day. It is crucial that information updating methodologies be sorted for assignment purposes, the accuracy have be done specially in the waiting section ([37],[46]). If there were no appropriate vehicle, the requests would wait in a queue for satisfying some pre-planned ones, until enough capacity for accomplishing requests in the queue is acquired. After completing a request, all new requests placed in the queue is checked, and the first request found to be appropriate for a remaining vehicle capacity is assigned, and the queue is sorted again. Determined orders have to be inserted in appropriate routes, and then appropriate modification should take place. A diagram for this process is shown in Figure 2 and described in the following algorithm. A pseudo code of the DVRP strategy is considered below.Algorithm 1: The DVRP strategyFor each time slice, doWhile there are new requests, doPut new requests in a sorted queue.For each request in the queue orderly, doConsider appropriate vehicles with enough capacities as candidates.Sort the candidates based on the cost function.If it is feasible to insert new request in current time slice, thenUpdate the adaptive memory in each insertion.ElsePut the request in the next slice.End IfApply the routing method (ACS/Insertion heuristic) and assign new requests.Apply improving methods on the best solutions found.New current solution= A complete feasible reconstructed solution.End ForEnd WhileEnd For.
, where T is the length of the working day. It is crucial that information updating methodologies be sorted for assignment purposes, the accuracy have be done specially in the waiting section ([37],[46]). If there were no appropriate vehicle, the requests would wait in a queue for satisfying some pre-planned ones, until enough capacity for accomplishing requests in the queue is acquired. After completing a request, all new requests placed in the queue is checked, and the first request found to be appropriate for a remaining vehicle capacity is assigned, and the queue is sorted again. Determined orders have to be inserted in appropriate routes, and then appropriate modification should take place. A diagram for this process is shown in Figure 2 and described in the following algorithm. A pseudo code of the DVRP strategy is considered below.Algorithm 1: The DVRP strategyFor each time slice, doWhile there are new requests, doPut new requests in a sorted queue.For each request in the queue orderly, doConsider appropriate vehicles with enough capacities as candidates.Sort the candidates based on the cost function.If it is feasible to insert new request in current time slice, thenUpdate the adaptive memory in each insertion.ElsePut the request in the next slice.End IfApply the routing method (ACS/Insertion heuristic) and assign new requests.Apply improving methods on the best solutions found.New current solution= A complete feasible reconstructed solution.End ForEnd WhileEnd For.3.2. The Insertion Heuristic
- The insertion of new customers is quite a complicated task and consideration is needed either for partial or for full re-planning of the non-visited part of the routes. After determining the position, the circuits are broken into routes with the last station as the departure and the depot as a destination for each vehicle (route). Then, ACS, to be described in detail in the next section, would be applied to find a minimal cost for responding to requests. If there is more than one request, requests are processed in the order of their entrances.Alternatively, there are different approaches in the literature to face with new customers. Our study compares ACS with the insertion idea for incoming orders arisen from the insertion heuristic, which was firstly proposed in[53].We use some modifications on this method. Established upon this heuristic, the necessary and sufficient conditions for feasibility of inserting a customer, say
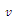 , between
, between 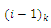 and
and 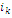 (as the last customer of kth vehicle and the depot, respectively) on a partially feasible route
(as the last customer of kth vehicle and the depot, respectively) on a partially feasible route 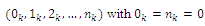 are:
are: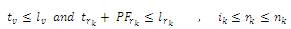 | (3) |
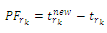 | (4) |
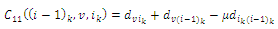 | (5) |
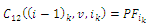 | (6) |
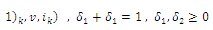 | (7) |
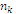 would be updated. The involved parameters in the above insertion heuristic affect the best feasible place for an un-routed customer. Provision of service to a customer is dependent on a weighed combination of distance to the place and time window violation. A pseudo code of the algorithm can now be given.
would be updated. The involved parameters in the above insertion heuristic affect the best feasible place for an un-routed customer. Provision of service to a customer is dependent on a weighed combination of distance to the place and time window violation. A pseudo code of the algorithm can now be given.4. The Hybrid Ant Colony System
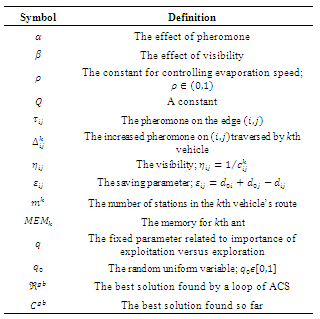
- Here, we describe a methodology for finding the shortest path by using ACS in order to find enough good solutions in real time events. The proposed method hybridizes the mechanism of ACS and some updating and exploration searches. Discussion on ACS as an applicable algorithm for combinatorial optimization problems can be found in[15], but here we give some explanations about the current approach on this well-known meta-heuristic algorithm. The notations used in the ACS algorithm are presented in Table 3.
|
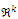 .Update the tabu list, pheromone, and data structure (local updating).End ForNeighborhood search {mutation operator, cross, and 2-opt exchanges}.New current solution = The best (non tabu) solution in the neighborhood.If the current solution is better than the best so far, thenThe best overall solution
.Update the tabu list, pheromone, and data structure (local updating).End ForNeighborhood search {mutation operator, cross, and 2-opt exchanges}.New current solution = The best (non tabu) solution in the neighborhood.If the current solution is better than the best so far, thenThe best overall solution 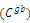 = The current solution.End IfUpdate the tabu list, pheromone, and data structure (global updating).End WhileReturn the best overall solution.
= The current solution.End IfUpdate the tabu list, pheromone, and data structure (global updating).End WhileReturn the best overall solution.4.1. The Initial Solution
- The minimum travel time solution can include a number of vehicles more than the one obtained by a solution with a minimal number of vehicles (see[20]). A heuristic method such as the one gave in[53] may be used to minimize the number of vehicles. Generally, minimizing the number of vehicles is unsuitable for DVRP, because it leaves a low residual capacity for each vehicle to accommodate dynamic requests. Since time being a critical element in DVRP, we thus prefer to use all available vehicles to form the first seed of routes. Two different heuristic scenarios are surveyed to find the initial solution for known customers. Both utilize a seed to go on finding routes. One of them lets the vehicles service customers as much as possible and this is done based on using the nearest neighbor to the last serviced customer. In this way, some vehicles service a large number of customers, while some others serve none. Another scenario forms the routes around the seed in finding a suitable customer near the last serviced customer for each vehicle in order. The former scenario leads to finding better routes having lower costs. Because of the necessity for scattering vehicles in the environment in order to have quick reactions to the incoming requests, it is logically better to use the latter scenario for DVRP. Therefore, at the beginning of the work shift, each known customers is assigned to a pre-defined number of vehicles.To determine seeds of the routes, customers are assigned to vehicles using Eq. (1) as a cost function. Initially, a seed of routes is formed using known customers with minimum cost with respect to a single depot. When the size of the seed equals the number of routes, un-routed customers are inserted into these routes. This is done based on the cost incurred regarding the last inserted customer on each route. The insertion process is repeated until all static customers are visited.
4.2. The Neighborhood Searches
- Since a good structure is based on a robust infrastructure, we try to find good initial solutions. Hereby, accomplishing ACS, we used some additional heuristics. This was done by using some neighborhood searches over the initial solution to restrict the exchanges to consecutive customers in the routes. Three neighborhood structures were used to find new better solutions in any iteration. The mutation operator, cross, and 2-opt exchange heuristics played the main roles in searching the solution space.The idea of the mutation operation is to randomly mutate the route and then produce a new solution that is not far from the original one. The steps for the mutation operation are as follows:(1) Select the two routes from the parent solutions and determine the mutating point for each one. (2) Exchange the work stations in the different tours and generate the child solution.(3) Ensure that the child solution is counted as a local optimum.As stated in[23], among different exchanging methods, the cross exchange can yield better results than other neighborhood searches. In this case, two segments of different lengths are removed from the current solution. Then, each segment is reinserted at the location with the smallest detour. In other words, an arc of each route is deleted and two other arcs are inserted such that each resulting route has customers of both original routes. The 2-opt exchange can be applied to improve the tours. This move deletes two arcs from a route and adds two new ones to the same route (see[12]). This means that some randomized possible pair-wise exchanges of customer locations visited by individual vehicles are tested to find out whether there would be any improvement in the objective function.The indicated neighborhood search is used in the dynamic part of the problem leading to some chances for new customers to be designated to more appropriate routes. These exchanges may create invalid solutions, in which case routes should be modified to the nearest valid solution. After changes made to reconstructed routes, we modify routes to feasible solutions.
4.3. Pheromone Updating of ACS
- An adaptive learning technique in ACS is to update the pheromone to cause improvement of new solutions. The colonies exchange information through pheromone updating. This process in ACS is conducted by reducing the amount of pheromone on all edges in order to simulate the natural evaporation of the pheromone and to guarantee that no path becomes too dominant in local updating, Eq. (8), and insists on the best solution by maximizing the pheromone trail value in global updating, Eq. (9):
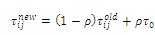 | (8) |
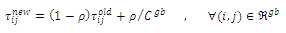 | (9) |
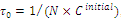 , where
, where 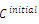 is the initial solution produced by a greedy heuristic, can make good initial pheromone trails on the arcs. In addition, we utilize the idea of ant-weight strategy rule for the pheromone increment updating[59]. The ant-weight strategy consists of two components: the global pheromone increment and the local pheromone increment. This updating method appropriates additional pheromone depending on the solution quality or the contribution of each link to the solution. The strategy is then written to be:
is the initial solution produced by a greedy heuristic, can make good initial pheromone trails on the arcs. In addition, we utilize the idea of ant-weight strategy rule for the pheromone increment updating[59]. The ant-weight strategy consists of two components: the global pheromone increment and the local pheromone increment. This updating method appropriates additional pheromone depending on the solution quality or the contribution of each link to the solution. The strategy is then written to be: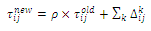 | (10) |
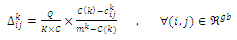 | (11) |
4.4. The Probability Function of ACS
- It can be said that pheromone trails give a measure of how much an arc is desirable to be inserted in a solution. In other words, these trails are used for exploration and exploitation. Based on the characteristic of ACS to select the next station j , the ant k at the current position of customer
 uses the probabilistic Eq. (12), as given below:
uses the probabilistic Eq. (12), as given below: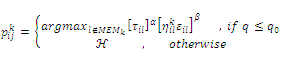 | (12) |
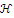 represents a random selecting method according to the probabilistic distribution of Eq. (12), as given below:
represents a random selecting method according to the probabilistic distribution of Eq. (12), as given below: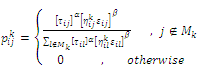 | (13) |
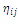 is usually counted as a static value, but in DVRP, it can be changed with respect to the corresponding time and distance of each arc, and so we have defined it as the inverse of distribution cost
is usually counted as a static value, but in DVRP, it can be changed with respect to the corresponding time and distance of each arc, and so we have defined it as the inverse of distribution cost 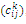 , which incorporates the combination of distance and travel time for each arc in each route. The value of the pheromone trail
, which incorporates the combination of distance and travel time for each arc in each route. The value of the pheromone trail 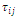 is dynamically changed.
is dynamically changed.5. Calibration of the Parameters and Operators
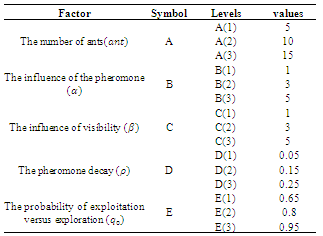
- Clearly, the values of parameters involved in the ACS algorithm directly or indirectly affect the quality of the final solution, and so control is needed for the result to be reliable. In order to determine the best combination of parameters for ACS, Taguchi’s method is used[48]. This method combines design of experiments and optimization of the control parameters based on the orthogonal array experiments and optimal settings of control parameters giving much reduced variance for the experiments. Exploring all parameter states is expensive and so selecting a candidate list as a representative for the search would be appropriate. We choose control factors including the number of ants
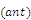 , the influence of the pheromone
, the influence of the pheromone 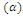 , the visibility
, the visibility 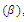 , the pheromone decay
, the pheromone decay 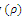 , and the probability exploration
, and the probability exploration 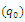 , which are respectively symbolized by A, B, C, D, and E. For each parameter, three quantities are investigated as shown in Table 4.
, which are respectively symbolized by A, B, C, D, and E. For each parameter, three quantities are investigated as shown in Table 4.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
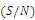 e ratio, which is log functions of desired output, serves as objective function for optimization, and helps in data analysis and prediction of optimum results. The
e ratio, which is log functions of desired output, serves as objective function for optimization, and helps in data analysis and prediction of optimum results. The 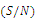 ratio representing the magnitude of the mean of a process compared to its variation as introduced by Taguchi is given by the following formulas:
ratio representing the magnitude of the mean of a process compared to its variation as introduced by Taguchi is given by the following formulas: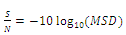 | (14) |
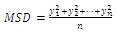 | (15) |
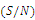 is exhibited in Figure 3, and Figure 4 confirms the level for each factor by using the mean of normalized objective function as a common performance measure.The mean square deviation (MSD) and
is exhibited in Figure 3, and Figure 4 confirms the level for each factor by using the mean of normalized objective function as a common performance measure.The mean square deviation (MSD) and 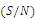 ratio are related to each other, and so for our study the larger
ratio are related to each other, and so for our study the larger 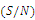 is better. To achieve better results, the following setting should be made for the factors: level 3 for factor A, level 3 for factor B, level 1 for factor C, level 2 for factor D, and level 2 for factor E. The analysis for parameter setting S/N ratio is done with ANOVA as exhibited in Table 6. With 95% confidence level, the level of factor B is not found to be considerable among the indicated levels here.
is better. To achieve better results, the following setting should be made for the factors: level 3 for factor A, level 3 for factor B, level 1 for factor C, level 2 for factor D, and level 2 for factor E. The analysis for parameter setting S/N ratio is done with ANOVA as exhibited in Table 6. With 95% confidence level, the level of factor B is not found to be considerable among the indicated levels here.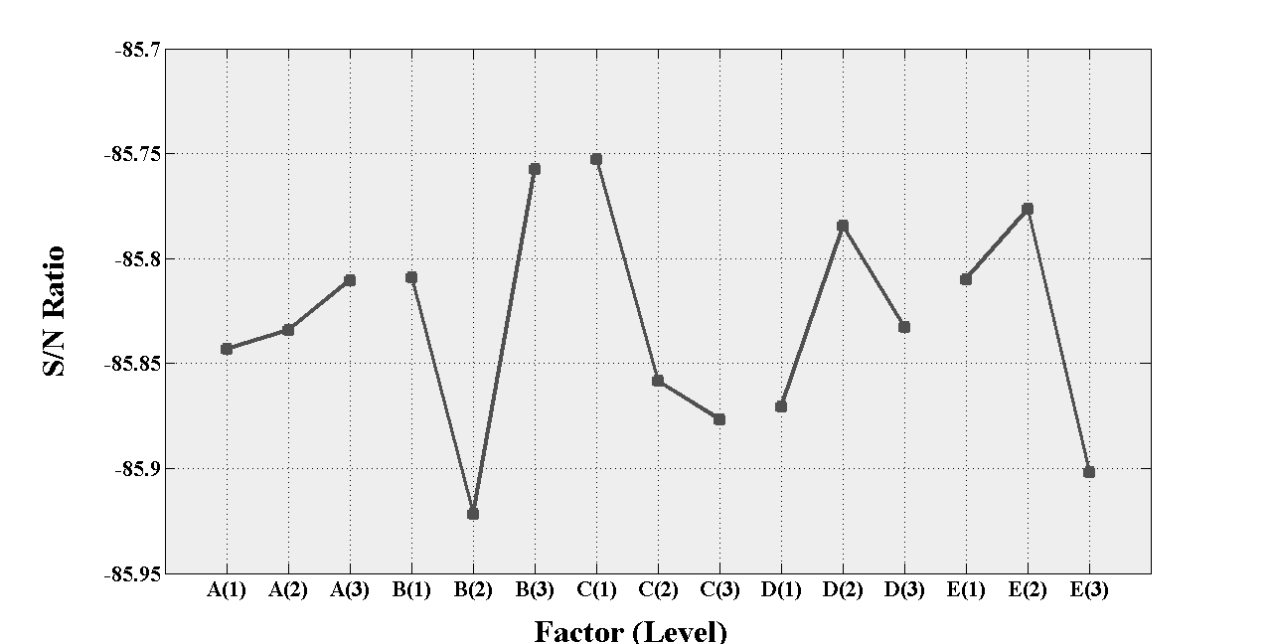 | Figure 3. The mean of ratio for each level of the ACS factors |
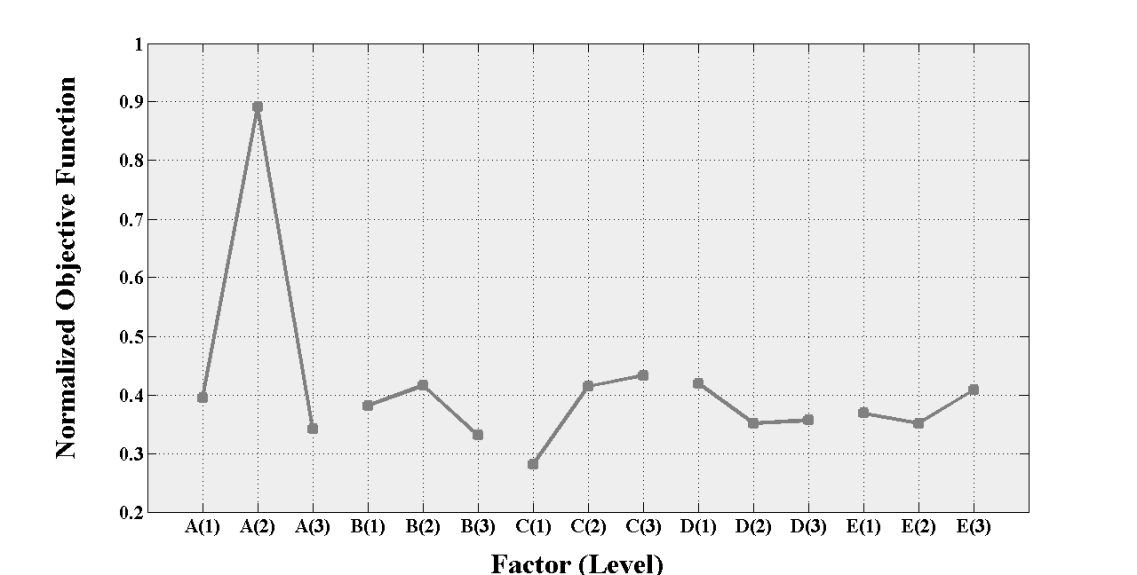 | Figure 4. The mean of normalized objective function for each level of the ACS factors |
|
 | Figure 5. An example of re-optimized route for incoming customers as time progresses |
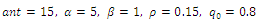 and for the parameters independent of the ACS process
and for the parameters independent of the ACS process 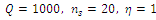 .In addition to the parameter setting for ACS, the parameters of the insertion method are set as
.In addition to the parameter setting for ACS, the parameters of the insertion method are set as 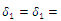
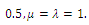 We used the same share of time and distance for our method.
We used the same share of time and distance for our method.6. Numerical Results and Discussion
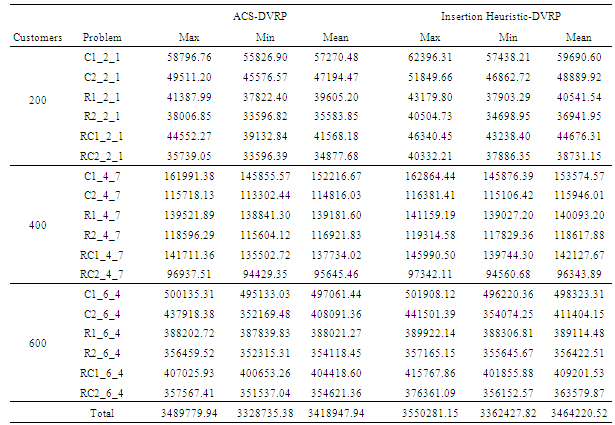
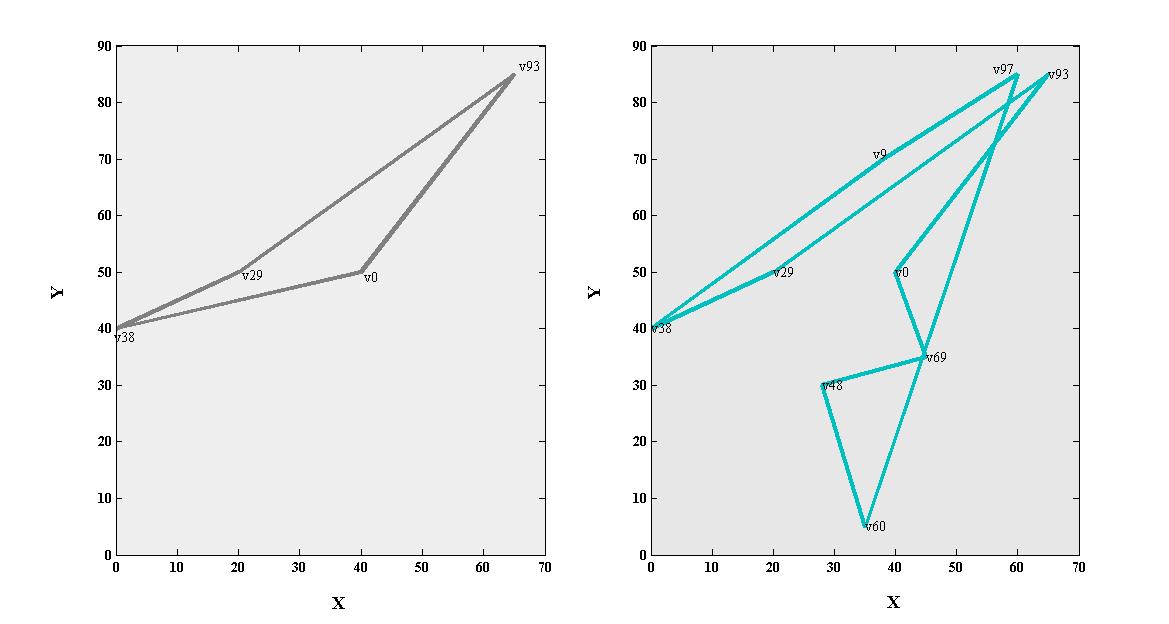
- The 56 benchmark problems of Solomon’s instances composed of six different problem types C1, C2, R1, R2, RC1,and RC2 were used to evaluate the developed ACS for DVRP. These problems contain between eight to twelve 100-node problems. The locations of customers in problem set R are generated as uniformly distributed random numbers in a square[0, 100] ×[0, 100]. For the test set C, the customers whose time windows are generated based on a known solution, are placed in clusters, and the test set RC is a combination of randomly placed and clustered customers. There are narrow time windows and small vehicle capacities for sets of type 1, and large time windows and large vehicle capacities for sets of type 2. Therefore, the solutions of type 2 problems have very few routes and significantly more customers per route.We supposed that about 40% of requests of these benchmarks appeared as dynamic requests depending on the order of the request in the original instances. The entrance rate
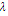 was adapted with the length of the working day T to consider each one of the 100 requests. The length of working day was set to the due date vehicles needed to return to the depot. Event manager was set to handle the immediate requests during the day after the advancing requests were serviced. We considered this uniform rate, because this seemed to be an intuitively correct approach for the performance of the dynamic system. For instance, Figure 5 graphically displays the entrance of static and dynamic customers for vehicle number 1 of C101 test problem. The route is extended from
was adapted with the length of the working day T to consider each one of the 100 requests. The length of working day was set to the due date vehicles needed to return to the depot. Event manager was set to handle the immediate requests during the day after the advancing requests were serviced. We considered this uniform rate, because this seemed to be an intuitively correct approach for the performance of the dynamic system. For instance, Figure 5 graphically displays the entrance of static and dynamic customers for vehicle number 1 of C101 test problem. The route is extended from 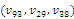 to
to 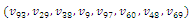 as the left and right subplots show respectively.Experiments on the algorithms were made in MATLAB® 7.6.0 (R2008a) environment, on a PC with 2.0GHz Intel Core® 2 Duo processor and 2GB RAM. Each test was conducted for four times, and the solution for each problem type is reported as the mean of the obtained results. First, the comparisons of three classes of Solomon’s instances are reported in Tables 7-9. These tables respectively represent the mean of the costs obtained by applying different neighborhood search methods on ACS-DVRP and insertion for the R, C and RC problem sets. The first column in each method titled COST is the result obtained by cost function, and the second column named DIST is the traveled distance. Figure 5 shows suitable operators for the problem with respect to distance or cost function. For example, the mutation operator is more appropriate for type 2 tests, and 2-Opt exchange is usually a good selection for type 1 tests. Our study considers cost functions located in the left side of the figure. Eventually, ACS-DVRP is suggested for developing a DVRP with the supposed attributes.
as the left and right subplots show respectively.Experiments on the algorithms were made in MATLAB® 7.6.0 (R2008a) environment, on a PC with 2.0GHz Intel Core® 2 Duo processor and 2GB RAM. Each test was conducted for four times, and the solution for each problem type is reported as the mean of the obtained results. First, the comparisons of three classes of Solomon’s instances are reported in Tables 7-9. These tables respectively represent the mean of the costs obtained by applying different neighborhood search methods on ACS-DVRP and insertion for the R, C and RC problem sets. The first column in each method titled COST is the result obtained by cost function, and the second column named DIST is the traveled distance. Figure 5 shows suitable operators for the problem with respect to distance or cost function. For example, the mutation operator is more appropriate for type 2 tests, and 2-Opt exchange is usually a good selection for type 1 tests. Our study considers cost functions located in the left side of the figure. Eventually, ACS-DVRP is suggested for developing a DVRP with the supposed attributes.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
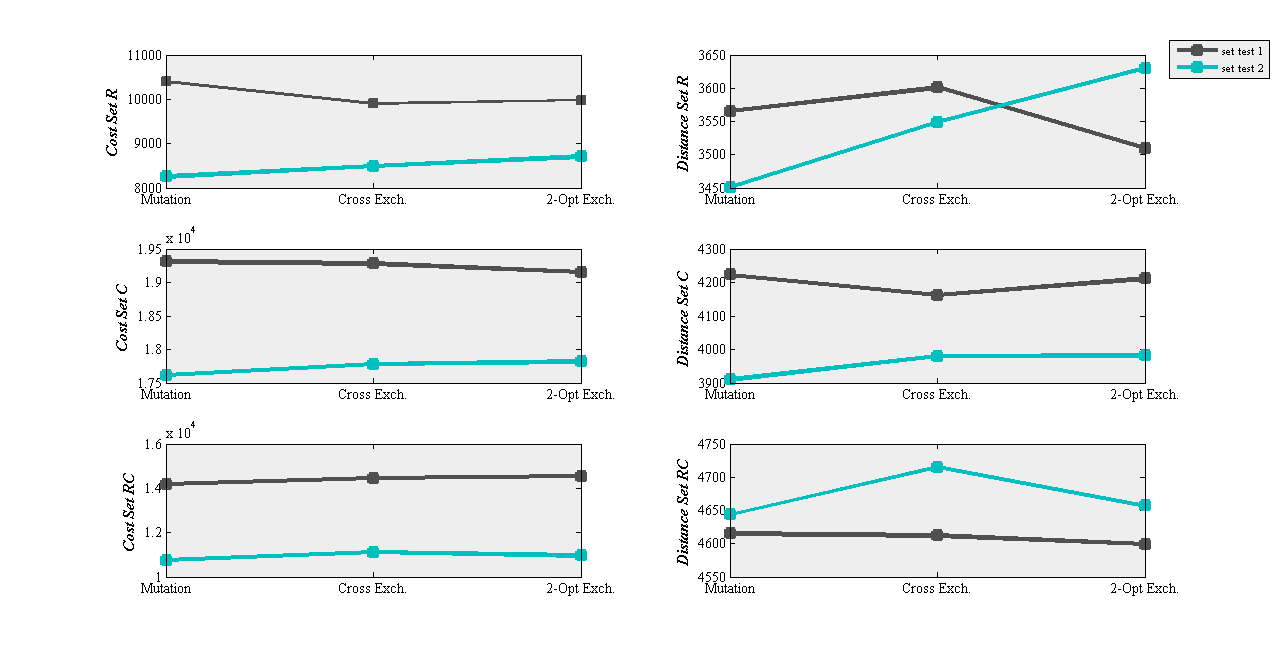 | Figure 6. The analysis for different operators on DVRP |
|
7. Conclusions
- In this paper, we proposed an ant colony system for dynamically responding requests in the vehicle routing problem. We used ACS besides neighborhood searches including mutation, cross and 2-opt exchange heuristics. As the procedure progresses, new solutions are created from the routes associated with previous solutions based on the defined objective function. The experimental results show that our hybrid ACS acts well for the supposed DVRP.It is important to notify that the approach is essentially domain-independent, and we expect that many other dynamic applications may benefit from this technique. Since time is a significant note on real time strategies, application of quick search strategies other than ACS are worth investigating. As further study, a simulation based study could be helpful to evaluate events for the considered problem. In addition, instead of certain probability distribution, uncertainty could be supposed, which there are rare studies in this regard such as reference[33].
ACKNOWLEDGEMENTS
- The authors would like to thank Professor Gilbert Laporte for his valuable comments that helped authors improve the paper.
References
| [1] | Archetti, C., Mansini, R. & Speranza, M.G. 2005, "Complexity and reducibility of the skip delivery problem", Transportation Science, vol. 39, no. 2, pp. 182-187. |
| [2] | Bent, R.W. & Van Hentenryck, P. 2004a, "Scenario-based planning for partially dynamic vehicle routing with stochastic customers", Operations Research, vol. 52, no. 6, pp. 977-987. |
| [3] | Bent, R. & Van Hentenryck, P. 2004b, "A two-stage hybrid local search for the vehicle routing problem with time windows", Transportation Science, vol. 38, no. 4, pp. 515-530. |
| [4] | Berbeglia, G., Cordeau, J. & Laporte, G. 2010, "Dynamic pickup and delivery problems", European Journal of Operational Research, vol. 202, no. 1, pp. 8-15. |
| [5] | Bertsimas, D.J. 1992, "A vehicle routing problem with stochastic demand", Operations Research, vol. 40, no. 3, pp. 574-585. |
| [6] | Branchini, R.,Moretti, Amaral Armentano, V. & Løkketangen, A. 2009, "Adaptive granular local search heuristic for a dynamic vehicle routing problem", Computers & Operations Research, vol. 36, no. 11, pp. 2955-2968. |
| [7] | Brotcorne, L., Laporte, G. & Semet, F. 2003, "Ambulance location and relocation models", European Journal of Operational Research, vol. 147, no. 3, pp. 451-463. |
| [8] | Chuah, K.H. & Yingling, J.C. 2005, "Routing for a just-in-time supply pickup and delivery system", Transportation Science, vol. 39, no. 3, pp. 328-339. |
| [9] | Cordeau, J.F. & Laporte, G. 2001, "A tabu search algorithm for the site dependent vehicle routing problem with time windows", INFOR, vol. 39, no. 3, pp. 292-298. |
| [10] | Cordeau, J.F. & Laporte, G. 2003, "A tabu search heuristic for the static multi-vehicle dial-a-ride problem", Transportation Research Part B: Methodological, vol. 37, no. 6, pp. 579-594. |
| [11] | Cordeau, J.F., Laporte, G. & Mercier, A. 2004, "Improved tabu search algorithm for the handling of route duration constraints in vehicle routing problems with time windows", Journal of the Operational Research Society, vol. 55, no. 5, pp. 542-546. |
| [12] | Croes, G.A. 1958, "A method for solving traveling-salesman problems", Operations Research, vol. 6, no. 6, pp. 791-812. |
| [13] | Dantzig, G.B. & Ramser, J.H. 1959, "The truck dispatching problem", Management Science, vol. 6, no. 1, pp. 80-91. |
| [14] | Dethloff, J. 2002, "Relation between vehicle routing problems: an insertion heuristic for the vehicle routing problem with simultaneous delivery and pick-up applied to the vehicle routing problem with backhauls", Journal of the Operational Research Society, vol. 53, no. 1, pp. 115-118. |
| [15] | Dorigo, M. & Blum, C. 2005, "Ant colony optimization theory: A survey", Theoretical Computer Science, vol. 344, no. 2-3, pp. 243-278. |
| [16] | Eksioglu, B., Vural, A.V. & Reisman, A. 2009, "The vehicle routing problem: A taxonomic review", Computers & Industrial Engineering, vol. 57, no. 4, pp. 1472-1483. |
| [17] | Erera, A.L., Savelsbergh, M. & Uyar, E. 2009, "Fixed routes with backup vehicles for stochastic vehicle routing problems with time constraints", Networks, vol. 54, no. 4, pp. 270-283. |
| [18] | Fleischmann, B., Gnutzmann, S. & Sandvoss, E. 2004, "Dynamic vehicle routing based on online traffic information", Transportation Science, vol. 38, no. 4, pp. 420-433. |
| [19] | Fu, L. 2002, "Scheduling dial-a-ride paratransit under time-varying, stochastic congestion", Transportation Research Part B: Methodological, vol. 36, no. 6, pp. 485-506. |
| [20] | Gambardella, L.M., Taillard, É. & Agazzi, G. 1999, "MACS-VRPTW: A multiple ant colony system for vehicle routing problems with time windows" in New Ideas in Optimization, eds. D. Corne, M. Dorigo & F. Glover, McGraw-Hill, London, UK, pp. 63-76. |
| [21] | Gendreau, M., Laporte, G. & Séguin, R. 1996, "Stochastic vehicle routing", European Journal of Operational Research, vol. 88, no. 1, pp. 3-12. |
| [22] | Gendreau, M. & Potvin, J. 1998, "Dynamic vehicle routing and dispatching" in Fleet management and logistics, eds. T.G. Crainic & G. Laporte, Kluwer, Boston, pp. 115-125. |
| [23] | Gendreau, M., Guertin, F., Potvin, J. & Taillard, E. 1999, "Parallel tabu search for real-time vehicle routing and dispatching", Transportation Science, vol. 33, no. 4, pp. 381-390. |
| [24] | Gendreau, M., Laporte, G. & Semet, F. 2001, "A dynamic model and parallel tabu search heuristic for real-time ambulance relocation", Parallel Computing, vol. 27, no. 12, pp. 1641-1653. |
| [25] | Ghiani, G., Guerriero, F., Laporte, G. & Musmanno, R. 2003, "Real-time vehicle routing: Solution concepts, algorithms and parallel computing strategies", European Journal of Operational Research, vol. 151, no. 1, pp. 1-11. |
| [26] | Guntsch, M. & Middendorf, M. 2001, "Pheromone modification strategies for ant algorithms applied to dynamic TSP" in Applications of Evolutionary Computing, ed. E. Boers, Springer Berlin / Heidelberg, , pp. 213-222. |
| [27] | Hanshar, F. & Ombuki-Berman, B. 2007, "Dynamic vehicle routing using genetic algorithms", Applied Intelligence, vol. 27, no. 1, pp. 89-99. |
| [28] | Hauptmeier, D., Krumke, S. & Rambau, J. 2000, "The Online Dial-a-Ride Problem under Reasonable Load" in Algorithms and Complexity, eds. G. Bongiovanni, R. Petreschi & G. Gambosi, Springer Berlin / Heidelberg, , pp. 125-136. |
| [29] | Hvattum, L.M., Lokketangen, A. & Laporte, G. 2006, "Solving a dynamic and stochastic vehicle routing problem with a sample scenario hedging heuristic", Transportation Science, vol. 40, no. 4, pp. 421-438. |
| [30] | Khouadjia, M., Alba, E., Jourdan, L. & Talbi, E. 2010, "Multi-swarm optimization for dynamic combinatorial problems: A case study on dynamic vehicle routing problem", Lecture Notes in Computer Science, vol. 6234, pp. 227-238. |
| [31] | Khouadjia, M.R., Sarasola, B., Alba, E., Jourdan, L. & Talbi, E. 2012, "A comparative study between dynamic adapted PSO and VNS for the vehicle routing problem with dynamic requests", Applied Soft Computing, vol. 12, no. 4, pp. 1426-1439. |
| [32] | Larsen, A., Madsen, O.B.G. & Solomon, M.M. 2007, "Classification Of Dynamic Vehicle Routing Systems" in Dynamic Fleet Management, eds. V. Zeimpekis, C.D. Tarantilis, G.M. Giaglis & I. Minis, Springer US, , pp. 19-40. |
| [33] | Lee, C., Le, K. & Park, S. 2011, "Robust vehicle routing problem with deadlines and travel time/demand uncertainty", Journal of the Operational Research Society, article in the press. |
| [34] | Madsen, O.B.G., Tosti, K. & Vælds, J. 1995a, "A heuristic method for dispatching repair men", Annals of Operations Research, vol. 61, no. 1, pp. 213-226. |
| [35] | Madsen, O., Ravn, H. & Rygaard, J. 1995b, "A heuristic algorithm for a dial-a-ride problem with time windows, multiple capacities, and multiple objectives", Annals of Operations Research, vol. 60, no. 1, pp. 193-208. |
| [36] | Meng, Q., Lee, D.H. & Cheu, R.L. 2005, "Multiobjective vehicle routing and scheduling problem with time window constraints in hazardous material transportation", Journal of Transportation Engineering, vol. 131, no. 9, pp. 699-707. |
| [37] | Mitrović Minić, S. & Laporte, G. 2004, "Waiting strategies for the dynamic pickup and delivery problem with time windows", Transportation Research Part B: Methodological, vol. 38, no. 7, pp. 635-655. |
| [38] | Moccia, L., Cordeau, J.F. & Laporte, G. 2012, "An incremental tabu search heuristic for the generalized vehicle routing problem with time windows", Journal of the Operational Research Society, vol. 63, no. 1, pp. 232-244. |
| [39] | Montemanni, R., Gambardella, L., Rizzoli, A. & Donati, A. 2005, "Ant colony system for a dynamic vehicle routing problem", Journal of Combinatorial Optimization, vol. 10, no. 4, pp. 327-343. |
| [40] | Nanry, W.P. & Barnes, J.W. 2000, "Solving the pickup and delivery problem with time windows using reactive tabu search", Transportation Research Part B: Methodological, vol. 34, no. 2, pp. 107-121. |
| [41] | Norin, A., Yuan, D., Granberg, T.A. & Värbrand, P. 2011, "Scheduling de-icing vehicles within airport logistics: a heuristic algorithm and performance evaluation", Journal of the Operational Research Society, article in the press. |
| [42] | Parragh, S.N., Doerner, K.F. & Hartl, R.F. 2010, "Variable neighborhood search for the dial-a-ride problem", Computers & Operations Research, vol. 37, no. 6, pp. 1129-1138. |
| [43] | Potvin, J.Y. & Naud, M.A. 2011, "Tabu search with ejection chains for the vehicle routing problem with private fleet and common carrier", Journal of the Operational Research Society, vol. 622, no. 2, pp. 326-336. |
| [44] | Powell, W.B. 1986, "A stochastic model of the dynamic vehicle allocation problem", Transportation Science, vol. 20, no. 2, pp. 117-129. |
| [45] | Psaraftis, H.N. 1995, "Dynamic vehicle routing: Status and prospects", Annals of Operations Research, vol. 61, no. 1, pp. 143-164. |
| [46] | Pureza, V. & Laporte, G. 2008, "Waiting and buffering strategies for the dynamic pickup and delivery problem with time windows", INFOR: Information Systems and Operational Research, vol. 45, no. 3, pp. 165-176. |
| [47] | Rei, W., Gendrea, M. & Soriano, P. 2010, "A hybrid Monte Carlo local branching algorithm for the single vehicle routing problem with stochastic demands", Transportation Science, vol. 44, no. 1, pp. 136-146. |
| [48] | Roy, R.K., 1990, A primer on the Taguchi method, Van Nostrand Reinhold, New York. |
| [49] | Sariklis, D. & Powell, S. 2000, "A heuristic method for the open vehicle routing problem", Journal of the Operational Research Society, vol. 51, no. 1, pp. 564-573. |
| [50] | Secomandi, N. & Margot, F. 2009, "Reoptimization approaches for the vehicle-routing problem with stochastic demands", Operations research, vol. 57, no. 1, pp. 214-230. |
| [51] | Seongmoon, K., Lewis, M.E. & White, C.C. 2005, "Optimal vehicle routing with real-time traffic information", IEEE Transactions on Intelligent Transportation Systems, vol. 6, no. 2, pp. 178-188. |
| [52] | Solomon, M.M. 1983, Vehicle routing and scheduling with time window constraints: models and algorithm, University of Pennsylvania. |
| [53] | Solomon, M.M. 1987, "Algorithms for the vehicle routing and scheduling problems with time window constraints", Operations Research, vol. 35, no. 2, pp. 254-265. |
| [54] | Süral, H. & Bookbinder, J.H. 2003, "The single-vehicle routing problem with unrestricted backhauls", Networks, vol. 41, no. 3, pp. 127-136. |
| [55] | Tan, K.C., Cheong, C.Y. & Goh, C.K. 2007, "Solving multi-objective vehicle routing problem with stochastic demand via evolutionary computation", European Journal of Operational Research, vol. 177, no. 2, pp. 813-839. |
| [56] | Torfi, F., Farahani, R.Z. & Mahdavi, I. 2011, "Fuzzy least-squares linear regression approach to ascertain stochastic demand in the vehicle routing problem", Applied Mathematics, vol. 2, no. 1, pp. 64-73. |
| [57] | Trudeau, P. & Dror, M. 1992, "Stochastic inventory routing: Route design with stockouts and route failures", Transportation Science, vol. 26, no. 3, pp. 171-184. |
| [58] | Xiang, Z., Chu, C. & Chen, H. 2008, "The study of a dynamic dial-a-ride problem under time-dependent and stochastic environments", European Journal of Operational Research, vol. 185, no. 2, pp. 534-551. |
| [59] | Yu, B., Yang, Z.Z. & Yao, B. 2009, "An improved ant colony optimization for vehicle routing problem", European Journal of Operational Research, vol. 196, no. 1, pp. 171-176. |
| [60] | Yu, B., Yang, Z.Z. & Xie, J.X. 2011, "A parallel improved ant colony optimization for multi-depot vehicle routing problem", Journal of the Operational Research Society, vol. 62, no. 1, pp. 183-188 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML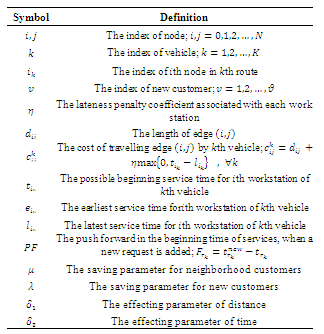
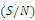 ratio
ratio