-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Operational Research
2012; 2(4): 27-30
doi: 10.5923/j.ajor.20120204.01
Formulation of Product Replacement Policies for Perishable Inventory Systems using Queuing Theoretic Approach
Rakesh Kumar , Sumeet Kumar Sharma
School of Mathematics, Shri Mata Vaishno Devi University, Katra, Sub Post- Office, University Campus, Postcode 182320, Jammu and Kashmir, India
Correspondence to: Rakesh Kumar , School of Mathematics, Shri Mata Vaishno Devi University, Katra, Sub Post- Office, University Campus, Postcode 182320, Jammu and Kashmir, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Inventory management plays a crucial role in managing production processes as well as the supply chains. The study of inventory systems with perishable products has a special significance as it influences the cost and revenue of a firm. Product replacement policies act like safeguards to the retailers (firms) dealing with the business of perishable products. The quantitative analysis of product replacement policies facilitates the decision making in the management of perishable inventory systems. In this paper, the cost-profit analysis of a single server, finite capacity Markovian queueing model with reneging and retention of reneged customers has been performed to study quantitatively the effect of product replacement policies (provided on perished products) on the cost and profit of the retailer. Some important measures of performance are also obtained for the detailed analysis of the model. Through this study, it has been observed that as the percentage of product replacement on perished products increases, the total expected cost of the retailer decreases and total expected profit increases.
Keywords: Perishable Products, Reneging, Markovian Queuing System, Product Replacement, Cost-profit Analysis
Article Outline
1. Introduction
- Queuing theory possesses its applications in a wide variety of areas. Particularly, it has played a significant role in inventory management. Queuing systems can be used for describing some types of perishable inventory systems as there is an analogy between queuing systems with reneging and perishable inventory systems. The on hand inventory can be considered as a queue, the demand completion as completion of service, the products coming in the form of replenishment as arrivals to the queuing system, and the life time of a product as the impatience (reneging) time. There is a considerable literature related to the modelling of perishable inventory systems using queuing systems with impatient customers. Customer reneging and product perishing are similar phenomena. A customer whose patience time expires leaves the queue and, likewise, a product made to stock whose lifetime expires is removed from the inventory.The first study of queuing with impatient customers appears to be that of Barrer[1]. He generalizes the standard M/M/1 queuing system to the case of impatient customers.He considers both the cases when the customers leave the system if service has not begin by a certain time, m (say) and where customer leaves the system if service is not completed by time m. The latter assumption is more appropriate for describing perishable inventories. William[14] makes a queuing model for an inventory problem. He derives the results for lost sales to the total demand in inventory systems using Markovian queuing setup. Sasieni[10] applies double queues and impatient customers to study inventory systems with perishable items. Nahmias[8] presents some queuing models for controlling perishable inventory. Graves and Keilson[2] model the production/ inventory problem as an M/M/1 queuing model. They apply the compensation method for minimizing the system costs consisting of setup costs, inventory holding costs and back order costs. Nahmias[9] presents a review on perishable inventory theory. In this paper, he reviews relevant literature on the problem of determining suitable ordering policies for both fixed life perishable inventory and inventory subject to continuous exponential decay. Graves[3] applies queuing theory to continuous perishable inventory systems. He obtains the steady-state distribution of the system inventory. Manuel et al.[7] study a stochastic perishable inventory system with random supply quantity. In this paper, they model the situation in which not all the items are useable and the supply may contain a fraction of defected items. They derive the limiting distribution of inventory level. Goswami et al.[4] consider the problem of determining the optimal retailer’s replenishment decisions for deteriorating items under two levels of trade-credit policy with in the economic production quantity framework. They investigate the retailer’s inventory system for deteriorating items as a cost minimization problem to determine the retailer’s optimal inventory policy. Shukla et al.[11] study an order level inventory model with three component demand rate for a newly launched deteriorating item. Teimoury et al.[13] apply queuing models for performance evaluation analysis in multi-product multi-echelon manufacturing supply chain network with batch ordering. According to Karaesmen and Deniz[5], in 2004, 22% of the unsalable costs incurred by distributors of consumer packaged goods are due to expired products, and 5.8% of all components of blood processed for transfusion are outdated. As a result, there is a continued need for understanding such systems and investigating the impact of the finiteness of product lifetimes on production and inventory control decisions. Shukla et al.[12] perform simulation of inventory policy for product with price and time dependent demand for deteriorating items. They study the effect of different parameters on optimal policy with simulation.The researchers in the interdisciplinary fields are constantly working towards formulation of product replacement strategies. The prevalence of decay, spoilage or expiry of an item in any perishable inventory system is really harmful and causes significant profit losses to such systems. In perishable inventory systems, the items become worthless when either their date of use expires or they are broken up or they lack specific requirements. In business transactions, the companies provide some safeguards to their customers (retailers) in the form of product replacements. The worthless items in perishable inventory systems may be regarded as impatient (reneged) customers. The product replacement schemes of a particular company ensure the replacement of defective items by non-defective ones to some extent or complete replacement. This type of replacement of items can be regarded as retention of reneged customers. Moreover finite number of items can be stored in the inventory of any retailer. For instance, in packaged food business, the packaged food items like burgers, pizzas, cheese’s sandwiches, hotdog’s etc. may get perished due to the expiry of their date of use, exposure to moisture and heat, improper packaging and the use of low quality raw materials. Usually the companies provide product replacement schemes to the retailers involved in such business as safeguards in order to maintain healthy retailer-supplier relationship. Through this paper one can study the long run effects of the different product replacement schemes on the retailer’s profit. Recently, Kumar and Sharma[6] study a finite capacity, single server, Markovian queuing model with balking and retention of reneged customers, and obtained steady-state solution. In this paper, the cost-profit analysis of a single-server, finite capacity Markovian queuing model with reneging and retention of reneged customers has been performed to study the effect of the percentage of product replacement (provided on the perished products) associated with different product replacement policies on the total expected profit of the retailer. Rest of the paper has been arranged as follows. In section 2, the model has been described. Section 3 deals with the steady-state solution. In section 4, the cost-profit analysis has been performed. The paper has been concluded in section 5.
2. Model Description
- The arrivals of items (customers) to the inventory (queue) occur in a Poisson stream one by one with an average arrival rate λ. The inter-arrival times (the inter-arrival times of incoming products to the retailer’s inventory) are independently, identically and exponentially distributed with parameter λ. There is only one server (retailer) and service times (the times at which the sale of a product from inventory takes place) are exponentially distributed with parameter μ. The items are sold in order of their arrival to the inventory i.e. the queue discipline is first–come, first- served (FCFS). The capacity of the system is taken as finite (say N ) as the retailer’s inventory can store a finite number of items in it. Each item (customer) upon arriving into the inventory (queue) may become worthless if it is not sold before its expiry date (i.e. reneged). The expiry (reneging) times of items follow exponential distribution with parameter
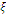 . An outdated item may be replaced by a new item ( i. e. retained) by the supplier (company) to the retailer with some probability, say, q in the form of its product replacement policy and may not be replaced with probability 1-q (= p).
. An outdated item may be replaced by a new item ( i. e. retained) by the supplier (company) to the retailer with some probability, say, q in the form of its product replacement policy and may not be replaced with probability 1-q (= p).3. Steady-state Solution of the Model
- Define,
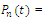 the probability that there are n customer in the system, that is,
the probability that there are n customer in the system, that is, 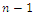 in the queue and one in service. The differential-difference equations of the model are:
in the queue and one in service. The differential-difference equations of the model are: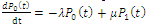 | (1) |
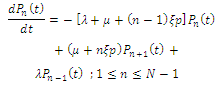 | (2) |
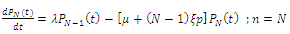 | (3) |
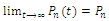 and therefore,
and therefore, 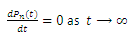 and hence, the solution of equations (1) to (3) gives:
and hence, the solution of equations (1) to (3) gives: 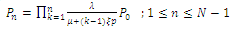 | (4) |
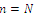 we get
we get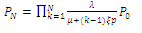 | (5) |
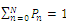 , we get
, we get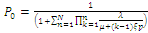 | (6) |
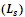 In the inventory case, this will be expected number of products in the inventory.
In the inventory case, this will be expected number of products in the inventory.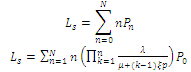 (ii) The Expected Number of Customers Served
(ii) The Expected Number of Customers Served  The expected number of customers served (demand completions) is given by:
The expected number of customers served (demand completions) is given by: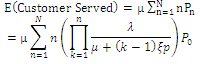 .(iii) Rate of Abandonment,
.(iii) Rate of Abandonment, 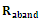 The average rate at which the customers (units in inventory) abandon (perish) is given by:
The average rate at which the customers (units in inventory) abandon (perish) is given by: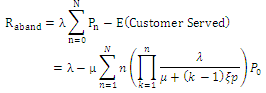 (iv) Expected number of waiting customers, who actually wait,
(iv) Expected number of waiting customers, who actually wait,  The actual number of units that remain in the inventory for their sale is given by:
The actual number of units that remain in the inventory for their sale is given by: 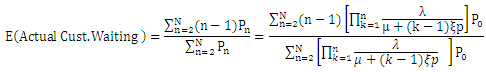 .Where P0 has been given in (6).
.Where P0 has been given in (6).4. Cost-Profit Analysis of the Model
- In this section the cost-profit analysis of the model has been carried out. Total expected cost, total expected revenue and total expected profit of the queuing system have been computed. For given values of different parameters (λ, µ etc.) the numerical results have been computed using MS-Excel. Various quantities of interest involved have been explained below:

 For a finite capacity system some customers can not join the system when they find that the system is full, then immediately they go elsewhere and are said to be lost from the system with rate λlost = number of lost customers per unit time.Thus,
For a finite capacity system some customers can not join the system when they find that the system is full, then immediately they go elsewhere and are said to be lost from the system with rate λlost = number of lost customers per unit time.Thus, 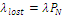 , where
, where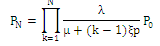 Where
Where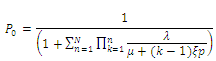 .We can obtain the average reneging rate
.We can obtain the average reneging rate 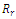 as follows:
as follows: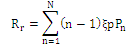 .Where
.Where 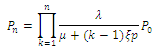 .The total expected cost (TEC) of the system is:
.The total expected cost (TEC) of the system is: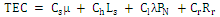 .Let R be the earned revenue for providing service to each customer per unit time then RLs would be total earned revenue for providing service to average number of customers in the system. Also, λRPN and RRr would be the losses in the revenue of the system due to capacity constraint and reneging of customers respectively. Hence, total expected revenue (TER) of the system is given by
.Let R be the earned revenue for providing service to each customer per unit time then RLs would be total earned revenue for providing service to average number of customers in the system. Also, λRPN and RRr would be the losses in the revenue of the system due to capacity constraint and reneging of customers respectively. Hence, total expected revenue (TER) of the system is given by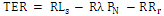 .Now, total expected profit (TEP) of the system is defined as:
.Now, total expected profit (TEP) of the system is defined as: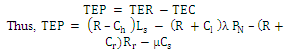 .Numerically, the impact of probability of retaining the impatient customers (q) on the profit obtained is shown in table-1. We have taken λ=2, μ=3, ξ = 0.1, N=4, Cs=18, Ch=8, Cr=6, and R=75. From table-1, we can see that as the probability of retaining the reneged customers (percentage of product replacement on perished products) increases, the total expected revenue of the system increases because of the increase in expected system size due to customer retention, while the total expected cost decreases. This in turn results in the increase in the total expected profit (TEP) of the system with the increase in probability of retaining the reneged customers. The value of TEP is minimum when q=0 (the case of no product replacement) and it is maximum when q=1 (the case of 100% product replacement on perished products). Thus, a retailer can know the variation in total expected profit and total expected cost with the change in probability of retaining the reneged customers, q (percentage of product replacement on perished products) and can decide about the percentage of product replacement to be demanded from the supplier.
.Numerically, the impact of probability of retaining the impatient customers (q) on the profit obtained is shown in table-1. We have taken λ=2, μ=3, ξ = 0.1, N=4, Cs=18, Ch=8, Cr=6, and R=75. From table-1, we can see that as the probability of retaining the reneged customers (percentage of product replacement on perished products) increases, the total expected revenue of the system increases because of the increase in expected system size due to customer retention, while the total expected cost decreases. This in turn results in the increase in the total expected profit (TEP) of the system with the increase in probability of retaining the reneged customers. The value of TEP is minimum when q=0 (the case of no product replacement) and it is maximum when q=1 (the case of 100% product replacement on perished products). Thus, a retailer can know the variation in total expected profit and total expected cost with the change in probability of retaining the reneged customers, q (percentage of product replacement on perished products) and can decide about the percentage of product replacement to be demanded from the supplier.5. Conclusions
- This paper provides a queuing perspective to study the perishable inventory systems with product replacement. A single server, finite capacity Markovian queueing model with reneging and retention of reneged customers is proposed and steady-state solution is obtained iteratively. Some important measures of performances are also derived. The cost-profit analysis of the model is carried out and the effect of percentage of product replacement on the cost and profit of the retailer is studied. It is observed that the total expected profit of the retailer increases as the percentage of product replacement on perished products increases. This model provides the quantitative basis for the study of product replacement policies and their effect on retailer’s business.This model is studied from the retailer’s prospective only. It can be studied from the supplier’s prospective also. A competitive game theoretic approach can be applied to take into account both the supplier as well as retailer’s profit to obtain optimal level of product replacement to be provided on perished products.Further, the model deals with single server only, it can be extended to multi-server case. This study is limited to finite capacity, it can further be generalized for infinite capacity.
References
| [1] | Barrer, D. Y., 1957, Queuing with impatient customers and indifferent clerks, Operations research, 5, 644-649. |
| [2] | Graves, S.C., and Keilson, J., 1981, The compensation method applied to a one-product production/inventory problem, Mathematics of Operations Research, 6 (2), 246-262. |
| [3] | Graves, S.C., 1982, The application of queuing theory to continuous perishable inventory systems, Management Science, 28 (4), 400-406. |
| [4] | Goswami, A., Mahata, G.C. and Prakash, O., 2010, Optimal retailer replenishment decisions in the EPQ model for deteriorating items with two level of trade credit financing. International Journal of Mathematics in Operational Research, 2 (1), 17–39. |
| [5] | Karaesmen, I., S.-W. A. and Deniz, B., 2011, Managing perishable and aging invetories: review and future research directions. in planning production and inventories in the extended enterprise, a state of the art handbook, Vol. 1, 393–438, Kempf, K., Keskinocak, P. and Uzsoy, P. (eds.), International Series in Operations Research and Management Science, Springer. |
| [6] | Kumar, R. and Sharma, S. K., 2012, An M/M/1/N queuing model with retention of reneged customers and balking, American Journal of Operational Research, 2(1), 1-5. |
| [7] | Manuel, P., and Lawrence, A.S., 2007, A stochastic perishable inventory system with random supply quantity, International Journal of Information and Management Sciences, 18(4), 317-334. |
| [8] | Nahmias, S., 1980, Queuing models for controlling perishable inventories, Proc. First Symp. Inventories, Budapest, 449–457. |
| [9] | Nahmias, S., 1982, Perishable inventory theory: a review. Operations Research, 30 (4), 680-708. |
| [10] | Sasieni, M. W., 1961, Double queues and impatient customers with an application to inventory theory, Operations Research, 9 (6), 771-781. |
| [11] | Shukla, D. and Khedlekar, U.K., 2010, An order level inventory model with three component demand rate (TCDR) for a newly launched deteriorating item, International Journal of Operations Research, 7 (2), 61-70. |
| [12] | Shukla, D., Khedlekar, U.K., Chandel, R..P.S., and Bhagwat, S., 2012, Simulation of inventory policy for product with price and time dependent demand for deteriorating items, International Journal of Modelling, Simulation and Scientific Computing, 3 (1), 115001-1-30. |
| [13] | Teimoury, E., Mazlomi, A., Nadafioun, R.,Khondabi, I.G., and Fathi, M.,2011, Inventory planning with batch ordering in multi-echelon multi-product supply chain by queuing approach, Proceeding of International Multi-Conference of engineering and computer scientists, 2, IMECS -2011, Hong Kong. |
| [14] | William, K., 1957, A queuing model for an inventory problem, Operations Research, 5 (5), 693-703. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML