-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Operational Research
2012; 2(1): 1-5
doi: 10.5923/j.ajor.20120201.01
An M/M/1/N Queueing Model with Retention of Reneged Customers and Balking
Rakesh Kumar , Sumeet Kumar Sharma
School of Mathematics, Shri Mata Vaishno Devi University, Katra, Sub Post- Office, University Campus, Postcode 182320,
Correspondence to: Rakesh Kumar , School of Mathematics, Shri Mata Vaishno Devi University, Katra, Sub Post- Office, University Campus, Postcode 182320,.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The concept of customer balking and reneging has been exploited to a great extent in recent past by the queuing modelers. Economically, if we see, the customer impatience (due to balking and reneging) leads to the loss of potential customers and thereby results into the loss in the total revenue. Taking into consideration this customers’ loss due to impatience, a new queuing model has been developed that deals with retention of reneged customers. According to this model, a reneged customer can be convinced in many cases by employing certain convincing mechanism to stay in the queue for completion of his service. Thus, a reneged customer can be retained in the queuing system with some probability (say, q) and it may leave the queue without receiving service with probability p (=1-q). This process is referred to as customer retention. We consider a single server, finite capacity queuing system with customer retention and balking in which the inter-arrival and service times follow negative-exponential distribution. The reneging times are assumed to be exponentially distributed. An arriving customer may not join the queue if there is at least one customer in the system, i.e. the customer may balk. The steady state solution of the model has been obtained. Some performance measures have been computed. The sensitivity analysis of the model has been carried out. The effect of probability of retention on the average system size has been studied. The numerical results show that the average system size increases proportionately and steadily as the probability of retention increases. Some particular cases of the model have been derived and discussed.
Keywords: Customer Retention, Reneging, Balking, Steady-State Solution, Sensitivity-Analysis, Finite Capacity
Cite this paper: Rakesh Kumar , Sumeet Kumar Sharma , "An M/M/1/N Queueing Model with Retention of Reneged Customers and Balking", American Journal of Operational Research, Vol. 2 No. 1, 2012, pp. 1-5. doi: 10.5923/j.ajor.20120201.01.
Article Outline
1. Introduction
- In the current scenario of population explosion and globalization of international commerce and trade, the queuing problems have gained a lot of significance in the decision making process. Queuing theory has revolutionized the industry and logistics sector apart from its immense applications in many other areas like city traffic, air traffic, bio-sciences, population studies, health sector etc. Queuing models have been built according to the prevailing demands or situation. The concept of customer impatience in queuing has been introduced in 1950’ and still people are exploiting this concept in various applications[1-11]. A customer is said to be impatient if he tends to join the queue only when a short wait is expected and tends to remain in the line if his wait has been sufficiently small. Impatience generally takes three forms. The first is balking, the reluctance of a customer to join a queue upon arrival, the second reneging, the reluctance to remain in line after joining and waiting, and the third jockeying between lines when each of a number of parallel lines has its own queue[12]. The notion of customer impatience appeared in the queuing theory in the work of Haight[13] in 1957. He considered a model of balking for M/M/1 queue in which there is a greatest queue length at which an arrival would not balk. This length was a random variable whose distribution was same for all customers. Haight[14] studied a queue with reneging in which he studied the problem like how to make rational decision while waiting in the queue, the probable effect of this decision etc. Ancker et al[15] studied
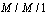 queuing system with balking and reneging and performed its steady state analysis. Ancker et al[16] also obtained results for a pure balking system (no reneging) by setting the reneging parameter equal to zero. Queuing theory has successfully been applied to various congestion (queuing) situations involving revenue generation through servicing customers. Aforementioned queuing systems deal with the customers’ loss due to impatience (balking or reneging) which results into a substantial reduction in the total revenue. Customer impatience has become the burning problem of private as well as government sector enterprises. They are constantly working towards customer retention for better future prospects. In this paper, we consider a single server, finite capacity queuing system with customer retention and balking, in which the inter-arrival and service times follow negative-exponential distribution. Each customer upon arriving in the queue will wait a certain length of time for service to begin. If it has not begun by then, he will get impatient and leave the queue without getting service. This time is a random variable and follows exponential distribution. An impatient customer (due to reneging) can be made to stay in service system for his service by utilizing certain convincing mechanism. Such customers are termed as retained customers. When a customer gets impatient (due to reneging), he may leave the queue with some probability say and may remain in the queue with some other probability
queuing system with balking and reneging and performed its steady state analysis. Ancker et al[16] also obtained results for a pure balking system (no reneging) by setting the reneging parameter equal to zero. Queuing theory has successfully been applied to various congestion (queuing) situations involving revenue generation through servicing customers. Aforementioned queuing systems deal with the customers’ loss due to impatience (balking or reneging) which results into a substantial reduction in the total revenue. Customer impatience has become the burning problem of private as well as government sector enterprises. They are constantly working towards customer retention for better future prospects. In this paper, we consider a single server, finite capacity queuing system with customer retention and balking, in which the inter-arrival and service times follow negative-exponential distribution. Each customer upon arriving in the queue will wait a certain length of time for service to begin. If it has not begun by then, he will get impatient and leave the queue without getting service. This time is a random variable and follows exponential distribution. An impatient customer (due to reneging) can be made to stay in service system for his service by utilizing certain convincing mechanism. Such customers are termed as retained customers. When a customer gets impatient (due to reneging), he may leave the queue with some probability say and may remain in the queue with some other probability 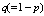 . An arriving customer may not join the queue if there is at least one customer in the system, i.e. the customer may balk. The steady state solution of the model has been obtained. Some queuing models have been obtained as particular cases of the model. The sensitivity of the analysis model has been carried out to show the impact of customer retention probabilities on the measures of performances like expected system size etc. A comparative study of the present model with two other related models has also been carried out.Rest of the model has been arranged as follows: section 2 deals with the formulation of stochastic queuing model, in section 3, the differential-difference equations of the model have been made, in section 4, the steady-state solution of the model has been derived, section 5 deals with the sensitivity analysis of the model, section 6, deals with the particular cases of the model with comparative analysis and in section 7, the paper has been concluded.
. An arriving customer may not join the queue if there is at least one customer in the system, i.e. the customer may balk. The steady state solution of the model has been obtained. Some queuing models have been obtained as particular cases of the model. The sensitivity of the analysis model has been carried out to show the impact of customer retention probabilities on the measures of performances like expected system size etc. A comparative study of the present model with two other related models has also been carried out.Rest of the model has been arranged as follows: section 2 deals with the formulation of stochastic queuing model, in section 3, the differential-difference equations of the model have been made, in section 4, the steady-state solution of the model has been derived, section 5 deals with the sensitivity analysis of the model, section 6, deals with the particular cases of the model with comparative analysis and in section 7, the paper has been concluded. 2. Stochastic Queuing Model
- The queuing model under consideration is based on following assumptions:1. The arrivals occur in a Poisson stream one by one with an average arrival rate λ. The inter-arrival times are independently, identically and exponentially distributed with parameter λ.2. There is only one server and service times are exponentially distributed with parameter μ.3. The queue discipline is first–come, first- served (FCFS).4. The capacity of the system is taken as finite (say N).5. Each customer upon arriving in the queue will wait a certain length of time (reneging time) for service to begin. If it has not begun by then, he will get impatient and may leave the queue without getting service with probability P and may remain in the queue for his service with probability
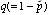 . The reneging times follow exponential distribution with parameter
. The reneging times follow exponential distribution with parameter 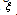 . 6. The arriving customers balk with probability n/N, where n is the number in system and N is the maximum number allowed in the system.
. 6. The arriving customers balk with probability n/N, where n is the number in system and N is the maximum number allowed in the system. 3. Derivation of Differential-Difference Equations
- Define,
 = the probability that there are
= the probability that there are 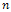 customer in the system, that is, n-1 in the queue and one in service. For
customer in the system, that is, n-1 in the queue and one in service. For 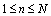 , in an infinitesimally small interval
, in an infinitesimally small interval 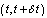
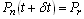 {there are
{there are 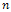 customer in the system at time
customer in the system at time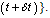 It can happen in the following mutually-exclusive ways: i On arrival a customer either decides to join the queue with probability (1-n/N) or balks with probability n/N when n customers are ahead of him (n = 0, 1, ...,N−1). The system might be in state n at time t and during the time interval of length
It can happen in the following mutually-exclusive ways: i On arrival a customer either decides to join the queue with probability (1-n/N) or balks with probability n/N when n customers are ahead of him (n = 0, 1, ...,N−1). The system might be in state n at time t and during the time interval of length 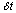 , no arrival, no departure and no reneging occurs.ii The system might be in state n at time t, an arrival and a departure both occur during the time interval of length
, no arrival, no departure and no reneging occurs.ii The system might be in state n at time t, an arrival and a departure both occur during the time interval of length 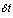 .iii The system might be in state n-1 at time t and an arrival takes place during the time interval of length
.iii The system might be in state n-1 at time t and an arrival takes place during the time interval of length 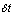 . iv The system might be in state n+1 at time t, a departure takes place and no arrival occurs during the time interval of length
. iv The system might be in state n+1 at time t, a departure takes place and no arrival occurs during the time interval of length 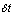 . v The system might be in state at time t and during the interval of length
. v The system might be in state at time t and during the interval of length 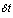 , a reneged customer with probability
, a reneged customer with probability 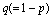 does not abandon the queue i.e. he stays in the system for his service.vi The system might be in state n+1 at time t and during the interval of length
does not abandon the queue i.e. he stays in the system for his service.vi The system might be in state n+1 at time t and during the interval of length 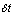 an impatient customer with probability p abandons the queue.Hence, for
an impatient customer with probability p abandons the queue.Hence, for 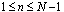 Finding the difference
Finding the difference 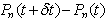 , dividing both sides by
, dividing both sides by 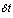 and taking limit
and taking limit 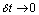 leads to equation (2).
leads to equation (2). 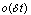 approaches to zero as rapidly as
approaches to zero as rapidly as 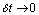 Similarly, other equations can be derived.The differential-difference equations of the model are:
Similarly, other equations can be derived.The differential-difference equations of the model are: 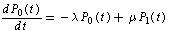 | (1) |
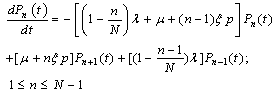 | (2) |
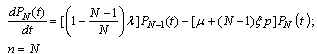 | (3) |
4. Steady-State Solution
- In steady state,
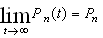 and therefore
and therefore 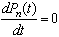 as
as 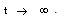 Thus, the steady-state equations corresponding to equations (1) - (3) are as follows:
Thus, the steady-state equations corresponding to equations (1) - (3) are as follows: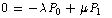 | (4) |
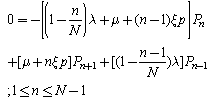 | (5) |
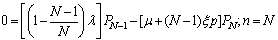 | (6) |
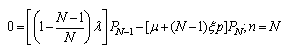 | (7) |
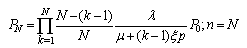 | (8) |
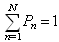 , we get
, we get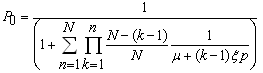 | (9) |
5. Sensitivity Analysis
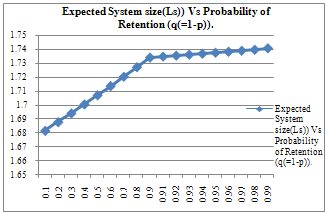
- For n=4 and different value of
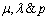 , we haveCASE-1: Variation of Expected System Size with the variation in Average Arrival RateWhen
, we haveCASE-1: Variation of Expected System Size with the variation in Average Arrival RateWhen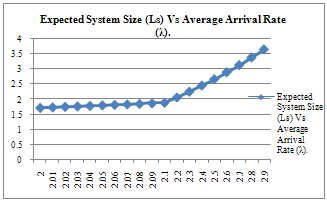 | Figure 1. |
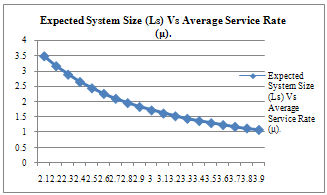 | Figure 2. |
 | Figure 3. |
 | Figure 4. |
6. Particular Cases
- i When the probability of retention, q=0The model reduces to M/M/1/N queuing model with reneging and balking with
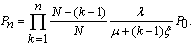 | (10) |
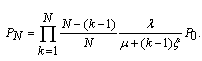 | (11) |
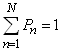 , we get
, we get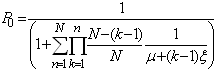 | (12) |
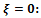 The model reduces to a simple M/M/1/N queue with balking with
The model reduces to a simple M/M/1/N queue with balking with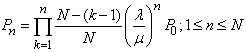 | (13) |
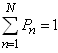 , we get
, we get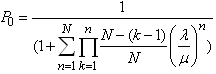 | (14) |
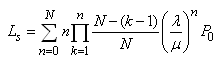 | (15) |
7. Conclusions
- This paper discussed a Markovian single server finite capacity queuing model with balking and possibilities of retaining reneged customers. The introduction of this concept of customer retention in queuing models has a lot of significance in the revenue generating queuing systems. The steady-state probabilities of system size have been obtained and some measures of performance have also been computed. The effect of parameters like average arrival rate, average service rate etc. have been studied numerically and it has been found that with the increase in probability of retention, the expected system size also increases proportionately and steadily. Some particular cases of the model have been discussed.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML