Rakesh Kumar1, Rajiv Kumar2, V. K. Sehgal2
1School of Mathematics, Shri Mata Vaishno Devi, University, Katra, Sub-Post-Office, University Campus, Post Code-182320, Jammu and Kashmir, India
2Department of Mathematical Science and Computer Applications, Bundelkhand University, Jhansi, India
Correspondence to: Rakesh Kumar, School of Mathematics, Shri Mata Vaishno Devi, University, Katra, Sub-Post-Office, University Campus, Post Code-182320, Jammu and Kashmir, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Catastrophe modeling has been playing a pivot role in the situations prone to disasters. But the study of recovery from catastrophic destruction is also important as any catastrophized system cannot function normally without its repair/recovery. To this end, a single server queuing system with catastrophic and restorative effects has been developed. The arrivals to the queuing system occur in correlated batches of variable size. The service times are exponentially distributed. The stochastic queuing model has been made. The time-dependent solution of the model has been obtained using probability generating function technique. The probability generation function of the system size has been obtained in Laplace transform form. Some queuing models have been derived as particular cases of this model.
Keywords:
Correlated Bulk Arrivals, Restoration, Catastrophes, Transient Solution, Stochastic Queuing Model
Cite this paper: Rakesh Kumar, Rajiv Kumar, V. K. Sehgal, Time-Dependent Solution of a Queuing System with Correlated Bulk Arrivals, Catastrophe and Restoration, American Journal of Operational Research, Vol. 1 No. 1, 2011, pp. 1-4. doi: 10.5923/j.ajor.20110101.01.
1. Introduction
Queuing models have been used in the design and performance evaluation of computer-communication networks. Particularly, in broadband networks, the cell traffic generated is correlated in nature[1]. Solo[2] also studied some queuing models with correlated arrival process in broadband communication networks. Adas[3] surveyed and examined traffic models that are currently used in the literature. He discussed some traditional short-range and non-traditional long-range dependent traffic models in broadband networks. Jain and Kumar[4-7] studied some queuing models for broadband networks subject to catastrophes (i.e. attack of viruses, noise bursts tec.). Jain and Kumar[8] introduced the concept of restoration in catastrophic queues. According to them, any system suffering from catastrophe will always require some sort of time to function in a normal way, which is taken as restoration time. During the process of restoration, no arrival is allowed to the system. Kumar[9,10] studied correlated input queuing models with catastrophic and restorative effects for cell traffic generated by broadband services. Di Crescenzo et al[11] studied a double ended queuing model with catastrophes and repair and obtained the transient and steady-state solutions. Tarabia[12] performed the transient and steady-state analysis of an M/M/1queue with balking, catastrophes, server failures and repairs using the generating function and direct approach. Park et al[13] studied the GI/Geo/1 queue with catastrophes and obtained the steady state solution. Thangaraj and Vanitha[14] studied an M/M/1queue with catastrophes and obtained the transient solution using continued fractions. Bohm[15] discussed various queuing systems with total disasters. In this paper, we incorporate the effect of catastrophe and restoration in the correlated batch arrival queue arising in Broadband Communication Networks. We consider a single server catastrophic-cum-restorative queuing model with correlated batch arrivals and exponential service. We derive the transient solution of the model under investigation.This paper has been organized as follows: In section 2, we formulate the stochastic queuing model. In section 3, we obtain the transient solution of the model. The paper has been concluded in section 4.
2. Formulation of the Stochastic Queuing Model
The queuing model under investigation is based on the following assumptions:(1) The customers arrive at a service facility in batches, the size of the batch being a random variable with Prob. (size of the batch is j) = cj ; j=1,2,3,…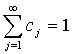 (2) The arrival of a batch can occur only at the transition marks t0, t1, t2…where r = tr – tr-1; r = 1,2,3,…are random variables with P [rx] = 1 –exp (-x); 0, r = 1,2,…The arrival and no arrival of a batch at two consecutive transition marks tr-1,tr; r=1,2,3,…are governed by the following transition probability matrix:
(2) The arrival of a batch can occur only at the transition marks t0, t1, t2…where r = tr – tr-1; r = 1,2,3,…are random variables with P [rx] = 1 –exp (-x); 0, r = 1,2,…The arrival and no arrival of a batch at two consecutive transition marks tr-1,tr; r=1,2,3,…are governed by the following transition probability matrix: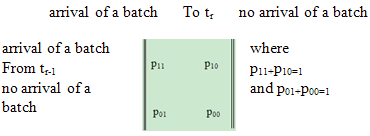 Thus, the arrivals of batches at two consecutive transition marks are correlated.(3) The queue discipline is first-come-first-served.(4) The capacity of the system is infinite.(5) There is a single server and the service is accomplished one by one. The service time distribution is exponential with parameter μ.(6) When the system is not empty, the catastrophes occur at the service facility according to a Poisson process of rate . The catastrophes annihilate all the customers in the system instantaneously. (7) The restoration times are independently, identically and exponentially distributed with parameter η.(8) Let the time be reckoned from the instant when the service channel is idle and a transition with no arrival has just occurred, so that Q 0,0(0)=1Define,Pn, 0(t) = the probability that at time t, the queue length (the number of customers waiting excluding those being served) is equal to n, the service channel is not idle and no arrival of a batch has occurred at the previous transition mark.P n, 1(t) = the probability that at time t , the queue length is equal to n, the service channel is not idle and an arrival of a batch has occurred at the previous transition mark.Q0, 0(t) = the probability that at time t, the queue length is equal to 0 without the occurrence of catastrophe, the service channel is idle and no arrival of a batch has occurred at the previous transition mark .C0, 0(t) =the probability that at time t, the queue length is equal to 0 with the occurrence of catastrophe, the service channel is idle and no arrival of a batch has occurred at the previous transition mark .Q0, 1(t) = the probability that at time t , the queue length is equal to 0 without the occurrence of catastrophe ,the service channel is idle and an arrival of a batch has occurred at the previous transition mark .C0, 1(t) = the probability that at time t , the queue length is equal to 0 with the occurrence of catastrophe ,the service channel is idle and an arrival of a batch has occurred at the previous transition mark .R n (t) = the probability that at time t, the queue length is equal to n.
Thus, the arrivals of batches at two consecutive transition marks are correlated.(3) The queue discipline is first-come-first-served.(4) The capacity of the system is infinite.(5) There is a single server and the service is accomplished one by one. The service time distribution is exponential with parameter μ.(6) When the system is not empty, the catastrophes occur at the service facility according to a Poisson process of rate . The catastrophes annihilate all the customers in the system instantaneously. (7) The restoration times are independently, identically and exponentially distributed with parameter η.(8) Let the time be reckoned from the instant when the service channel is idle and a transition with no arrival has just occurred, so that Q 0,0(0)=1Define,Pn, 0(t) = the probability that at time t, the queue length (the number of customers waiting excluding those being served) is equal to n, the service channel is not idle and no arrival of a batch has occurred at the previous transition mark.P n, 1(t) = the probability that at time t , the queue length is equal to n, the service channel is not idle and an arrival of a batch has occurred at the previous transition mark.Q0, 0(t) = the probability that at time t, the queue length is equal to 0 without the occurrence of catastrophe, the service channel is idle and no arrival of a batch has occurred at the previous transition mark .C0, 0(t) =the probability that at time t, the queue length is equal to 0 with the occurrence of catastrophe, the service channel is idle and no arrival of a batch has occurred at the previous transition mark .Q0, 1(t) = the probability that at time t , the queue length is equal to 0 without the occurrence of catastrophe ,the service channel is idle and an arrival of a batch has occurred at the previous transition mark .C0, 1(t) = the probability that at time t , the queue length is equal to 0 with the occurrence of catastrophe ,the service channel is idle and an arrival of a batch has occurred at the previous transition mark .R n (t) = the probability that at time t, the queue length is equal to n.
3. Transient Solution of the Model
The equations governing the model are: -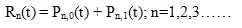 | (1) |
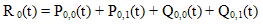 | (2) |
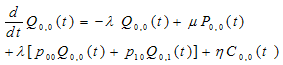 | (3) |
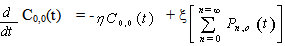 | (4) |
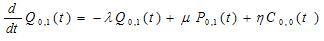 | (5) |
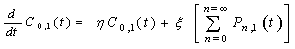 | (6) |
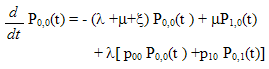 | (7) |
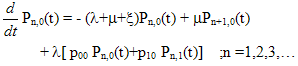 | (8) |
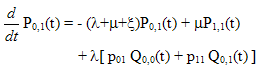 | (9) |
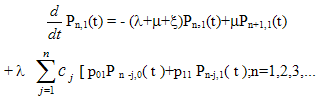 | (10) |
Define, the Laplace Transform of f(t) by 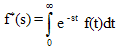 | (11) |
Taking L.T.,s of (1) to(8) ,we have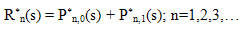 | (12) |
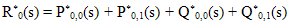 | (13) |
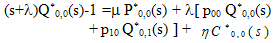 | (14) |
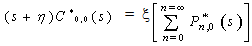 | (15) |
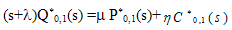 | (16) |
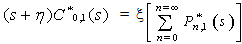 | (17) |
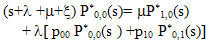 | (18) |
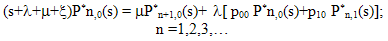 | (19) |
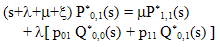 | (20) |
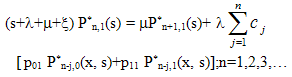 | (21) |
Define, the following probability generating functions by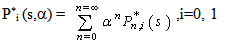 | (22) |
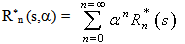 | (23) |
Multiplying (18) and (19) by appropriate powers of α and adding, we have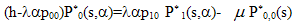 | (24) |
Similarly (20) and (21) give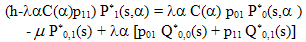 | (25) |
Where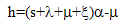 | (26) |
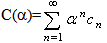 | (26.1) |
Also, (12) and (13) give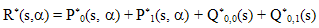 | (27) |
Solving (24) and (25) simultaneously, we have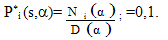 | (28) |
Where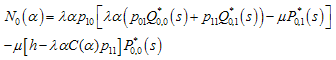 | (29) |
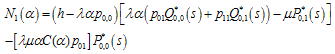 | (30) |
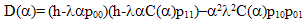 | (31) |
Combining (27) and (28) we get 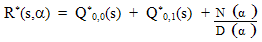 | (32) |
Where 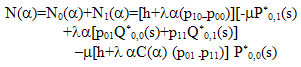 | (33) |
From (22) for α=1, we have 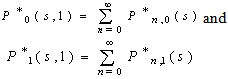 | (34) |
Substituting =1 in (24) and using (30), we have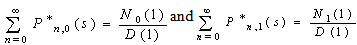 | (35) |
Also from (15) and (17), we have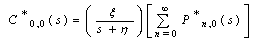 | (36) |
and 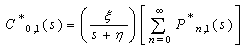 | (37) |
Thus, substituting the values of 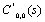 and
and  in (14) and (16) we get two equations in four unknowns. By Rouche’s theorem the denominator D(α) in (32) has two zeros inside the unit circle
in (14) and (16) we get two equations in four unknowns. By Rouche’s theorem the denominator D(α) in (32) has two zeros inside the unit circle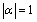 .Since R*(s,α) is a finite quantity these two zeros must vanish the numerator N(α) giving rise to two equations. Solving these two equations together with the equations obtained by substituting the value of
.Since R*(s,α) is a finite quantity these two zeros must vanish the numerator N(α) giving rise to two equations. Solving these two equations together with the equations obtained by substituting the value of 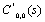 and
and 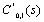 in equations (14) and (16) one can determine all the four unknowns viz., P*0,0(s), P*0,1(s), Q*0,0(s), Q*0,1(s). Hence, R*(s,α) can be completely determined.
in equations (14) and (16) one can determine all the four unknowns viz., P*0,0(s), P*0,1(s), Q*0,0(s), Q*0,1(s). Hence, R*(s,α) can be completely determined.
3.1. Particular Case-I
When =0 and η = ∞ (i.e. neither catastrophe nor restoration occurs), from (32), (36) and (37) we have 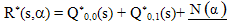 | (38) |
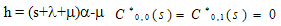 | (39) |
(38) provides the Laplace transform of the probability generating function of the system size of a single server queue with correlated batch input and exponential service time distribution.
3.2. Particular Case-II
When the arrivals occur one by one i.e. C (α) =α and η = ∞, from (32) we have 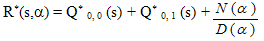 | (40) |
Where 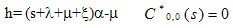 | (41) |
and 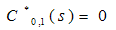 | (42) |
(40) - (42) provide the Laplace transform of the probability generating function of the system size of a catastrophic queuing system with correlated input which is studied by Jain and Kumar[4].
4. Conclusions
This paper studies a correlated bulk input queuing model with catastrophic and restorative effects. Time–dependent solution of the model has been arrived at using probability generating function technique. Some queuing models have been derived as particular cases of this model. The model can be useful in the study broadband communication traffic.
References
| [1] | Andrade Parra, J.,1993, Statistical parameters to describe cell traffic generated by broadband services, Communicaciones de Telefo′nica, 4(2), 81-88 |
| [2] | Solo, V., 1995, On queuing theory for broadband communication traffic with long range correlation, Proceedings of the 34th conference on decision and control, New Orleans, LA, 853-858 |
| [3] | Adas, A., 1997,Traffic models in broadband networks, IEEE Communications Magazine, 82-89 |
| [4] | Jain, N. K. and Kumar, R., 2005, A catastrophic queuing model with correlated input for the cell traffic generated by new broadband services, Indian journal of Mathematics and Mathematical sciences, 1(2), 99-108 |
| [5] | Jain, N. K. and Kumar, R., 2005,Transient solution of a correlated queuing problem with variable capacity and catastrophes, International Journal of Information and Management Sciences, 16(4), 39-47 |
| [6] | Jain, N. K. and Kumar, R., 2006, A catastrophic queuing system with correlated batch arrivals and variable service capacity, Bulletin of Pure and Applied Sciences’, 25E(1), 97-104 |
| [7] | Jain, N. K. and Kumar, R., 2005, M/G/1queue with catastrophes, Indian Journal of Mathematics and Mathematical Sciences,1(1), 45-50 |
| [8] | Jain, N. K. and Kumar, R., 2007, Transient solution of a catastrophic-cum- restorative queuing problem with correlated arrivals and variable service capacity’, International Journal of Information and Management Sciences,18(4), 461-465 |
| [9] | Kumar, R., 2008, A catastrophic-cum-restorative queuing system with correlated batch arrivals and variable capacity, Pakistan Journal of Statistics and Operations Research, 4(2), 55-62 |
| [10] | Kumar, R.,2009, A catastrophic-cum-restorative queuing model with correlated input for the cell traffic generated by new broadband services, African Journal of Mathematics and Computer Science Research, 2 (10), 225-229 |
| [11] | Di Crescenzo, A., Virginia G., Kumar, B. K., and Nobile, A. G., 2011, A double-ended queue with catastrophes and repairs,and a jump-diffusion approximation, Methodology and Computing in Applied Probability, e-print-arXiv/1101.5073, doi= 10.1007/s11009-011-9214-2 |
| [12] | Tarabia, A.M.K., 2011, Transient and steady-state analysis of an M/M/1queue with balking, catastrophes, server failures and repairs, Journal of Industrial and management optimization, 7(4), 811-823 |
| [13] | Park, H. M., Yang, W. S. and Chae, K. C., 2009, Analysis of GI/Geo/1 queue with disasters, Stochastic analysis and applications, 28(1), 44-53 |
| [14] | Thangaraj, V., and Vanitha, S., 2009, On the analysis of M/M/1feedback queue with catastrophes using continued fractions, International Journal of Pure and Applied Mathematics, 53(1), 133-151 |
| [15] | Bohm, W., 2008, A note on queuing systems exposed to disasters, http://statmath.wu-wien.ac.at/ |

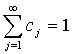 (2) The arrival of a batch can occur only at the transition marks t0, t1, t2…where r = tr – tr-1; r = 1,2,3,…are random variables with P [rx] = 1 –exp (-x); 0, r = 1,2,…The arrival and no arrival of a batch at two consecutive transition marks tr-1,tr; r=1,2,3,…are governed by the following transition probability matrix:
(2) The arrival of a batch can occur only at the transition marks t0, t1, t2…where r = tr – tr-1; r = 1,2,3,…are random variables with P [rx] = 1 –exp (-x); 0, r = 1,2,…The arrival and no arrival of a batch at two consecutive transition marks tr-1,tr; r=1,2,3,…are governed by the following transition probability matrix: Thus, the arrivals of batches at two consecutive transition marks are correlated.(3) The queue discipline is first-come-first-served.(4) The capacity of the system is infinite.(5) There is a single server and the service is accomplished one by one. The service time distribution is exponential with parameter μ.(6) When the system is not empty, the catastrophes occur at the service facility according to a Poisson process of rate . The catastrophes annihilate all the customers in the system instantaneously. (7) The restoration times are independently, identically and exponentially distributed with parameter η.(8) Let the time be reckoned from the instant when the service channel is idle and a transition with no arrival has just occurred, so that Q 0,0(0)=1Define,Pn, 0(t) = the probability that at time t, the queue length (the number of customers waiting excluding those being served) is equal to n, the service channel is not idle and no arrival of a batch has occurred at the previous transition mark.P n, 1(t) = the probability that at time t , the queue length is equal to n, the service channel is not idle and an arrival of a batch has occurred at the previous transition mark.Q0, 0(t) = the probability that at time t, the queue length is equal to 0 without the occurrence of catastrophe, the service channel is idle and no arrival of a batch has occurred at the previous transition mark .C0, 0(t) =the probability that at time t, the queue length is equal to 0 with the occurrence of catastrophe, the service channel is idle and no arrival of a batch has occurred at the previous transition mark .Q0, 1(t) = the probability that at time t , the queue length is equal to 0 without the occurrence of catastrophe ,the service channel is idle and an arrival of a batch has occurred at the previous transition mark .C0, 1(t) = the probability that at time t , the queue length is equal to 0 with the occurrence of catastrophe ,the service channel is idle and an arrival of a batch has occurred at the previous transition mark .R n (t) = the probability that at time t, the queue length is equal to n.
Thus, the arrivals of batches at two consecutive transition marks are correlated.(3) The queue discipline is first-come-first-served.(4) The capacity of the system is infinite.(5) There is a single server and the service is accomplished one by one. The service time distribution is exponential with parameter μ.(6) When the system is not empty, the catastrophes occur at the service facility according to a Poisson process of rate . The catastrophes annihilate all the customers in the system instantaneously. (7) The restoration times are independently, identically and exponentially distributed with parameter η.(8) Let the time be reckoned from the instant when the service channel is idle and a transition with no arrival has just occurred, so that Q 0,0(0)=1Define,Pn, 0(t) = the probability that at time t, the queue length (the number of customers waiting excluding those being served) is equal to n, the service channel is not idle and no arrival of a batch has occurred at the previous transition mark.P n, 1(t) = the probability that at time t , the queue length is equal to n, the service channel is not idle and an arrival of a batch has occurred at the previous transition mark.Q0, 0(t) = the probability that at time t, the queue length is equal to 0 without the occurrence of catastrophe, the service channel is idle and no arrival of a batch has occurred at the previous transition mark .C0, 0(t) =the probability that at time t, the queue length is equal to 0 with the occurrence of catastrophe, the service channel is idle and no arrival of a batch has occurred at the previous transition mark .Q0, 1(t) = the probability that at time t , the queue length is equal to 0 without the occurrence of catastrophe ,the service channel is idle and an arrival of a batch has occurred at the previous transition mark .C0, 1(t) = the probability that at time t , the queue length is equal to 0 with the occurrence of catastrophe ,the service channel is idle and an arrival of a batch has occurred at the previous transition mark .R n (t) = the probability that at time t, the queue length is equal to n.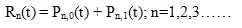
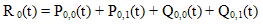
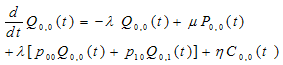
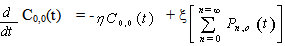
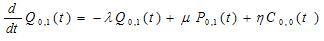
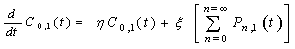
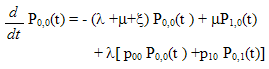
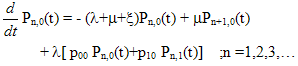
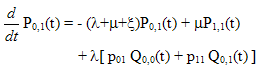
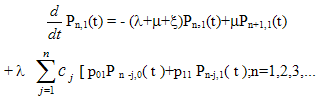
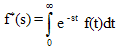
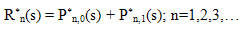
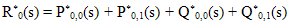
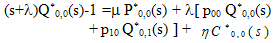
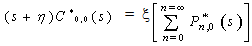
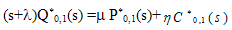
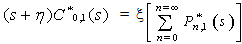
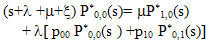
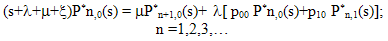
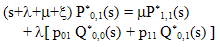
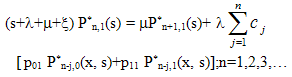
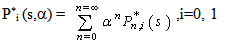
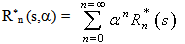
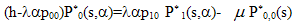
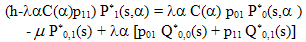
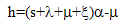
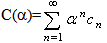
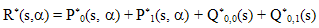
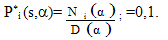
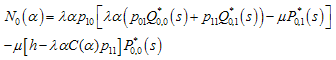
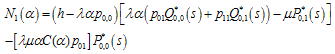
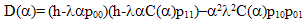
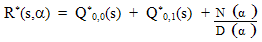
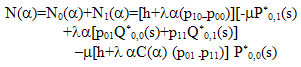
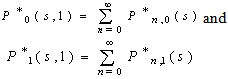
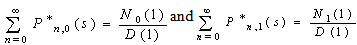
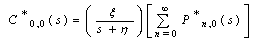
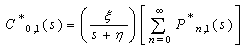
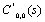 and
and  in (14) and (16) we get two equations in four unknowns. By Rouche’s theorem the denominator D(α) in (32) has two zeros inside the unit circle
in (14) and (16) we get two equations in four unknowns. By Rouche’s theorem the denominator D(α) in (32) has two zeros inside the unit circle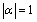 .Since R*(s,α) is a finite quantity these two zeros must vanish the numerator N(α) giving rise to two equations. Solving these two equations together with the equations obtained by substituting the value of
.Since R*(s,α) is a finite quantity these two zeros must vanish the numerator N(α) giving rise to two equations. Solving these two equations together with the equations obtained by substituting the value of 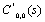 and
and 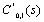 in equations (14) and (16) one can determine all the four unknowns viz., P*0,0(s), P*0,1(s), Q*0,0(s), Q*0,1(s). Hence, R*(s,α) can be completely determined.
in equations (14) and (16) one can determine all the four unknowns viz., P*0,0(s), P*0,1(s), Q*0,0(s), Q*0,1(s). Hence, R*(s,α) can be completely determined.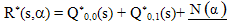
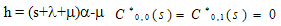
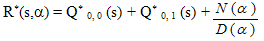
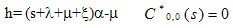
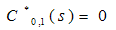
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML