1. Introduction

Coumarin occurs naturally in plants such as cinnamon, tonka bean and sweet clover. The coumarin content of these plants or their essential oils is highly variable, and these plants can be used in food supplements without any limit in coumarin content being indicated. Its structure was isolated by A. Vogel in 1820 from Tonka beans and synthesized in 1868 by W.H. Perkin, via the famous Perkin reaction, at high temperature, from salicylic aldehyde and an acid anhydride (CH₃CO)₂O in the presence of a weak base (CH3COONa). The process currently used by Rhodia, world leader on the market, also uses salicylic aldehyde in the synthesis of coumarin consuming approximately half of the annual production of salicylic aldehyde. These coumarin derivatives are also widely used as raw materials in the pharmaceutical, perfume and agrochemical industries, as starting materials or intermediates for the synthesis of various compounds with a wide range of biological activities [1-3]. These include antibacterial [1], antioxidant [2] and anti-inflammatory [3] properties.

In view of their importance and as an extension of our current research in the field of crystal structure analysis and theoretical calculations of new coumarin derivatives [4,5], we report here the synthesis, the spectroscopic characterization, the single-crystal X-ray diffraction (XRD) analysis, geometry optimization and Hirshfeld surface analysis of the ester derivative of coumarin scaffold (I).

2. Experimental and Theoretical Methods

2.1. Synthesis

The below reaction entails the O-acetylation of 6-hydroxycoumarin utilizing 4-methoxybenzoyl chloride as a reactant with tetrahydrofuran serving as a solvent and triethylamine as a base.

In this reaction, the used of HSAB theory suggests that hard bases like triethylamine provide optimum results when it concerns acylation of aromatic RCO⁺ acyl groups as hard acids [6].

So, in the current experiment, a solution containing 4-methoxybenzoyl chloride (6.17 mmol; 0.7 mL) in dried tetrahydrofuran (30-40 mL) was employed. Subsequently, dried triethylamine (2.6 mL; 3 molar equivalents) and 6-hydroxycoumarin (6.17 mmol; 1 g) were added gradually over 30 minutes. The mixture was then refluxed for 4 hours and mixed with 40 mL of chloroform. The pH of the solution was adjusted to 2-3 by adding diluted hydrochloric acid. The organic layer underwent extraction, was washed with water until it reached neutrality, then dried over magnesium sulfate (MgSO4) before removal of the solvent. The resulting crude product was suction-filtered, washed with n-hexane, and recrystallized from chloroform. Colorless crystals of the title compound were obtained in a good yield: 87 %. Mp 452-454 K.

2.2. Electrospray Ionization Mass Spectrum

Analysis were performed on a 3200 QTRAP spectrometer (Applied Biosystems SCIEX) equipped with a pneumatically assisted air pressure ionization (API) source for the ESI-MS⁺ experiment. The sample in solution was ionized under the following conditions: electrospray voltage (ISV): 5500 V; orifice voltage (OR): 20 V; nebulizing gas pressure (air): 10 psi. The mass spectrum (Figure 1) was obtained using a quadrupole mass spectrometer.

2.3. IR Spectrum

The infrared (IR) spectrum, Figure 2, was recorded on a Bruker IFS 66/S Fourier Transform Infrared spectrometer (FT-IR), driven by the OPUS 6.5 software and using the ATR (Attenuated Total Reflection) technique. The absorption bands are expressed in wavenumber ῡ (cm^-1).

2.4. NMR Spectra

¹H and ¹³C nuclear magnetic resonance (NMR) spectra were acquired using a Bruker AMX-400 spectrometer operating at 400 and 100 MHz, respectively. TMS was adopted as the internal standard, with chemical shifts recorded in δ ppm and coupling constants designated in Hz. Chloroform-d served as the solvation agent. Figures 3 and 4 depict these spectra.

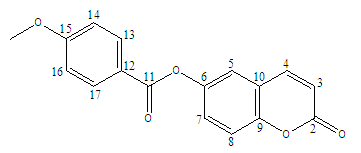Scheme 1. Numbering of carbon atoms used in spectra analysis.

2.5. Crystal structure Analysis

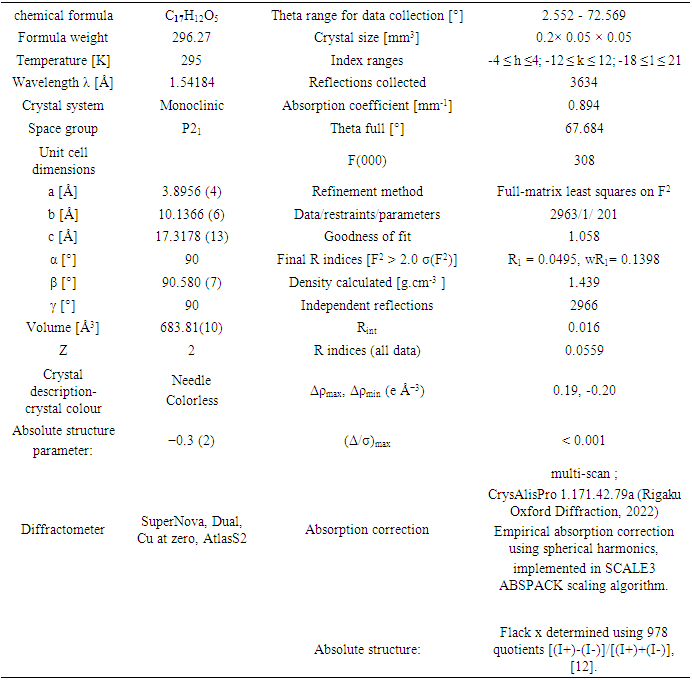
Diffraction data for the title compound were collected using a mirror monochromator and Cu Kα radiation (λ = 1.54184 Å) at 295 K on a Rigaku Oxford Diffraction SuperNova Dual, Cu at zero, AtlasS2 diffractometer [7]. The structure was solved via direct methods utilizing SIR 2014 [8] and implemented in the WinGX [9] program suite. The positional and anisotropic temperature parameters of the non-hydrogen atoms, which correspond to 201 crystallographic parameters, were refined using the SHELXL2014 program [10] through a full-matrix least squares method. The final refinement treated the structure as a 2-component twin with final BASF scale factors of 0.3559. All H atoms were placed in calculated positions [C—H = 0.93 Å (aromatic), 0.96 (methyl)] and refined using a riding model approximation with U_iso(H) restricted to 1.2 (aromatic) or 1.5 (methyl group) times U_eq of the respective parent atom.

Data collection, cell refinement and data reduction are by CrysAlis PRO [7].

The general-purpose crystallographic tool PLATON [11] was employed for the analysis and presentation of structural results. Details of the data collection conditions, and the parameters of the refinement process are given in Table 1. Flack x parameter was determined using 978 quotients [(I+)-(I-)]/[(I+)+(I-)] [12] for absolute structure determination.

CCDC-2304687 includes additional crystallographic data for this paper, which can be obtained at no cost from the Cambridge Crystallographic Data Centre via:

www.ccdc.cam.ac.uk/data_request/cif;

E-mail: deposit@ccdc.cam.ac.uk.

2.6. Hirshfeld Surface

Molecular Hirshfeld surfaces of 2-oxo-2H- chromen-6-yl 4-methoxybenzoate were computed with a standard (high) surface resolution and with the three-dimensional d_norm surfaces mapped over a fixed color scale from -0.117 (red) to 1.324 a.u. (blue) and shape index mapped over -1.000 to 1.000 a.u. using the program Crystal Explorer 3.1 [13].

2.7. Computational Procedures

The geometry optimization of compound (I) was performed using density functional theory (DFT) with the restricted RB3LYP exchange correlation functional and the restricted Hartree-Fock (RHF) methods with the 6-311⁺⁺G(d,p) basis set in ground state. Both calculations on (I) were performed using the starting geometries taken from the X-ray refinement data. Frequency calculation methods using the same basis sets were then performed with the optimized geometries to perform vibrational analysis, check the stability of the compounds, and obtain some thermodynamic parameters. All calculations were computed using the GAUSSIAN09 software package [14].

3. Results and Discussion

3.1. Spectra Analysis

3.1.1. Interpretation of Electrospray Ionization Mass Spectrum

The mass spectrum (Figure 1) displays two peaks detected at m/z 297 and 314 due respectively to the pseudo-molecular ion [M+H]⁺ and the ammonium adduct [M+NH₄]⁺, which confirm the molecular weight of 296 g.mol^-1 , in accordance with the chemical formula C₁₇H₁₂O₅.

ESI-MS m/z 297 [M+H]⁺; 314 [M+NH₄]⁺.

3.1.2. Infrared Spectrum

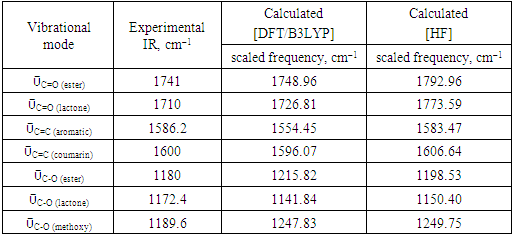
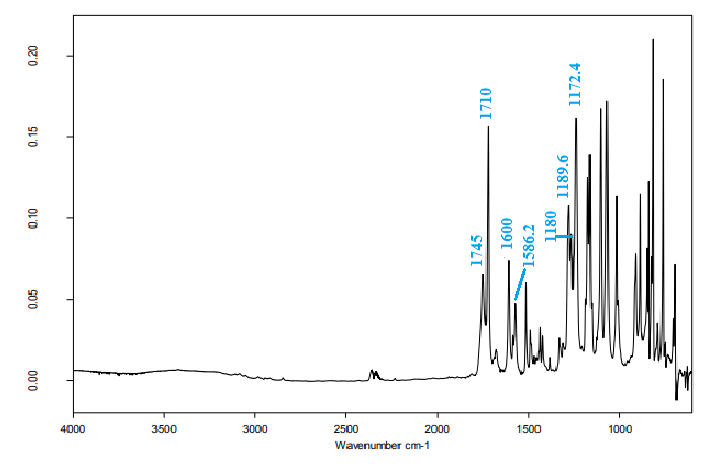
The FT-IR spectrum of the title compound (Figure 2) exhibits a medium band at 1741.0 cm^-1 that corresponds to ῡ_C=O (ester) and a strong absorption band at 1710.0 cm^-1 attributed to ῡ_C=O (lactone). Additionally, the observed bands at 1180.0, 1172.4, and 1189.6 cm^-1 can be assigned to (C−O, ester), (C−O, lactone) and (C−O, methoxy), respectively. The aromatic ring displayed a medium band ῡ_C=C at 1586.0 cm^-1 while the coumarinic ring exhibited it at 1600.0 cm^-1.

3.1.3. ¹H-NMR Spectrum

The ¹H NMR spectrum (Figure 3) analysis, including chemical shifts and coupling constants, revealed a total of six signals. Five of these signals were in the range of 6-8.5 ppm and were due to aromatic hydrogens. The remaining three methyl protons were observed unambiguously at 3.8 ppm.

The ¹H-NMR (CDCl₃, 400 MHz, δ ppm) data are as follows: 3.8 (s, 3H, CH3); 6.4 (d, 1H, J = 9.6 Hz, H-3); 7.0 (d, 2H, J = 8.9 Hz, H-14 and H-16); 7.38 (m, 3H, H-5, H-7, and H-8); 7.7 (d, 1H, J = 9.6 Hz, H-4); 8.3 (d, 2H, J = 8.9 Hz, H-13 and H-17).

3.1.4. ¹³C Attached-Proton-Test (APT) Spectrum

The Attached Proton Test NMR (APT NMR) is a ¹³C NMR experiment that reveals the number of protons that are attached to individual ¹³C carbon atoms in a molecule. So, it provides the information on all sorts of carbons within one experiment. Note that the peaks for CH and CH₃ point up, while the peaks for CH₂ and quarternary carbons including the solvent carbon point down.

The ¹³C APT NMR spectrum of the molecule in CDCl₃ (Figure 4) consists of 15 signals as expected. Eight peaks point up suggesting the nine aromatic tertiary carbons (C-3, C-4, C-5, C-7, C-8, C-13 and C-17, C-14 and C-16) and the shielded primary carbon of the methyl group ( CH3), whereas seven peaks point down indicating quaternary carbons (C-2, C-6, C-9, C- 10, C-11, C-12, C-15).

¹³C (APT)-NMR (CDCl₃, 100 MHz, δ ppm): 55.7 (CH₃), 114.2 (C-14 and C-16); 117.6 (C-3), 118.0 (C-5), 119.4 (C-12), 120.5 (C-7), 121.3 (C-10); 125.7 (C-8), 132.5 (C-13 and C-17); 142.9 (C-4), 147.2 (C-9), 151.7 (C-6), 160.76 (C-2), 164.4 (C-11), 164.9 (C-15).

3.1.5. Heteronuclear Single-Quantum Correlation (HSQC) NMR Spectrum

The HSQC-NMR spectrum (Figures 5) consists of eight spots exhibiting a good correlation on the one hand between the primary carbon and protons of methyl group and on the other hand between each tertiary carbon (C-3, C-4, C-5, C-7, C-8, C-14 and C-16, C-13 and C-17) and the proton directly attached by way of ¹J_C-H scalar coupling. The spots obtained confirm the attributions of signals in ¹H and ¹³C (APT)-NMR spectra.

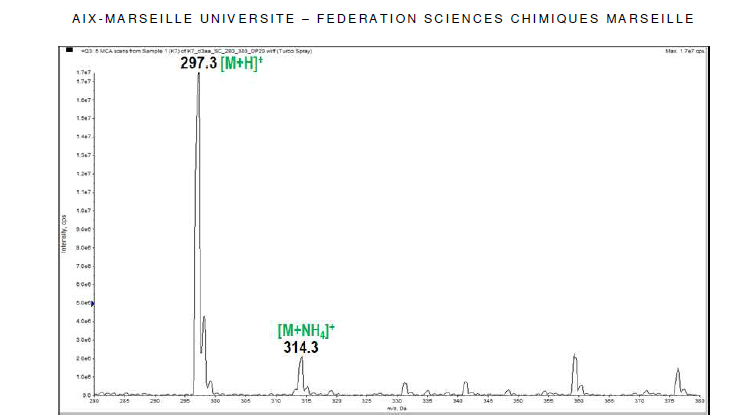Figure 1. Electrospray ionization mass spectrum of the molecule

Figure 2. 13C-NMR Spectrum of compound (I)

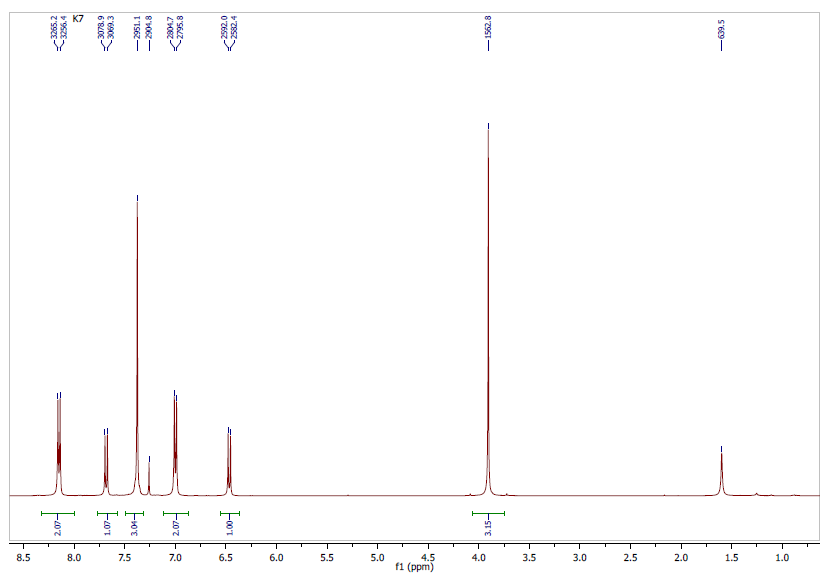Figure 3. Experimental 1H-NMR spectrum

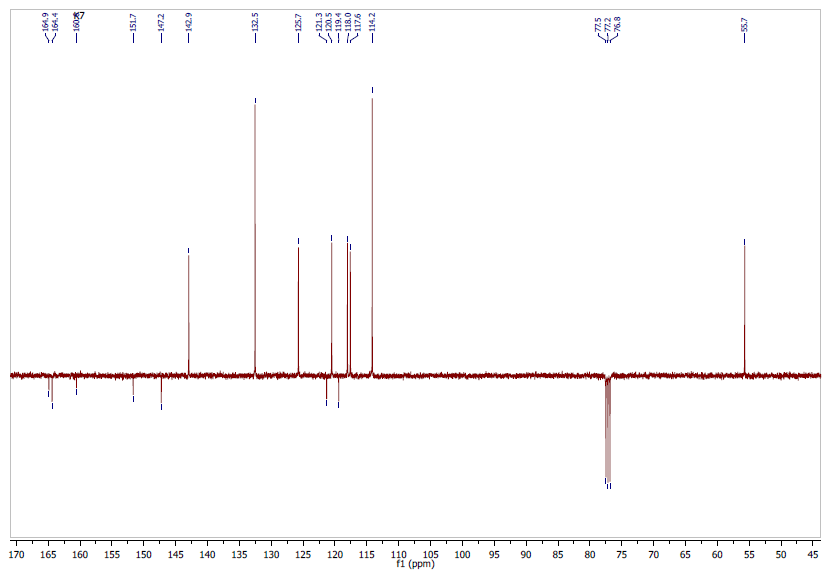Figure 4. Experimental 13C (APT)-NMR spectrum

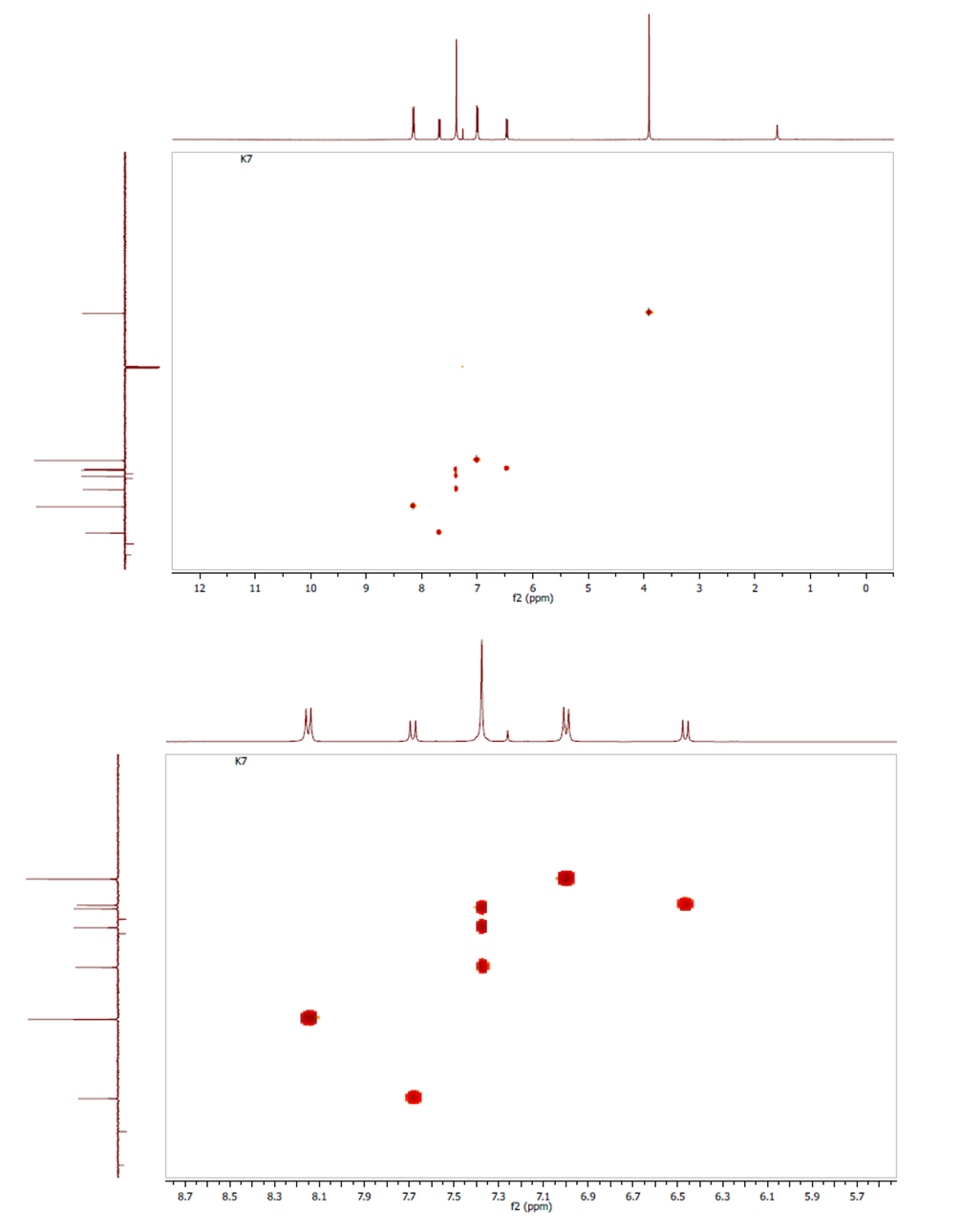Figures 5. Experimental HSQC spectra

3.2. Structural Description

The structure of the coumarin derivative (I) is shown in Figure 7.

3.2.1. Detection of Twinning

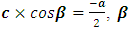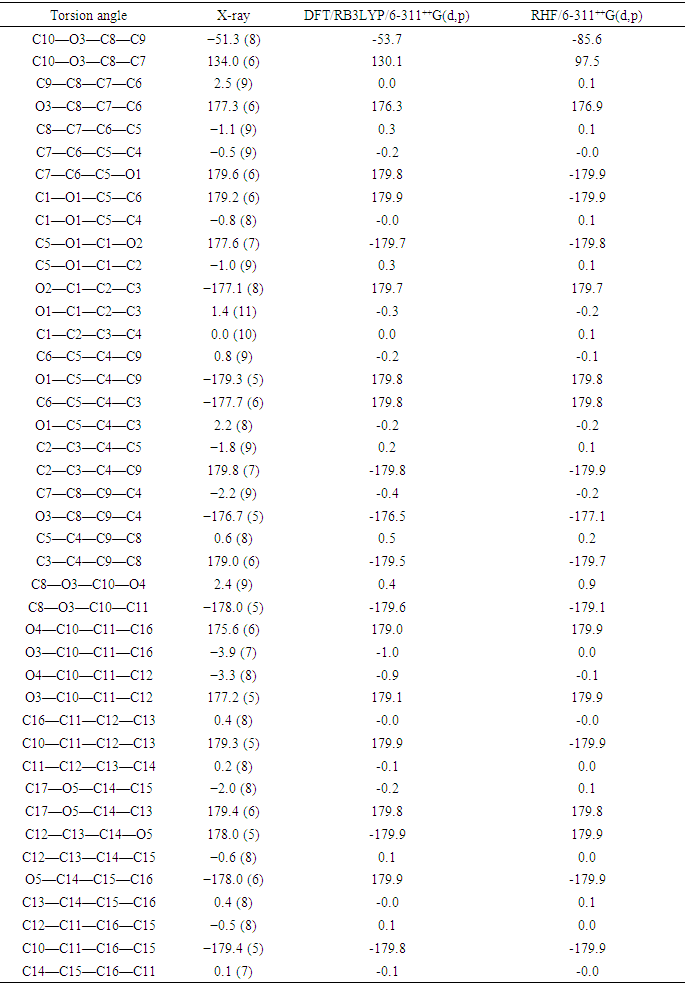
Two crystal lattices are considered to be twinned if they have similar orientations but a different geometry. Pseudo-merohedral twinning may occur in monoclinic crystal systems if the unit-cell parameters meet any of the following conditions: is close to 90°, or a is close to c [15]. In (I), the beta 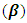value of 90.580(7)° clearly suggests a pseudo-merohedral twinning. Taking into account this molecular twinning in the refining process, including the twinning operator (l, -k, h) with the twinning fraction of 0.356(3), the crystallographic R₁ indice (discrepancy index) decreases significantly from 0.28 to 0.0495, table 1.

Table 1. Crystal data and details of the structure determination

3.2.2. Geometry and Conformation

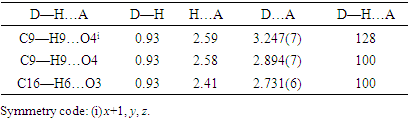
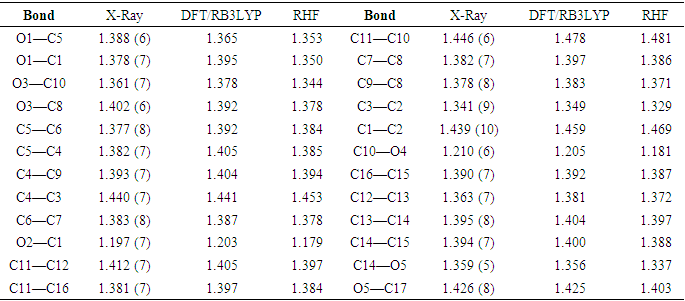
The tables, 4 through 7, display the positional parameters, interatomic distances, bond angles and torsion angles. The analysis and interpretation of the geometrical characteristics show that carbon-oxygen bonds, specifically d(C1-O1) = 1.378(7) Å and d(C5-O1) = 1.388(6) Å, have the same attributes as the Car-O(2) bond observed in other structures of alkyl ethers. These bond distances were compared to standard values [13]. Additionally, the measured distances of d(C10-O4) = 1.210(6) Å and d(C10-O3) = 1.361(7) Å indicate strong characteristics of the ester moiety. Furthermore, upon inspection of the bond lengths in the coumarin ring, it has been determined that there is a slight asymmetry in the electronic distribution around the pyrone ring: the C2—C3 [1.341 (9) Å] bond length is shorter, while the C1—C2 [1.439 (10) Å] bond length is longer than the expected Car—Car bond. This indicates that the electron density is lower in the C2-C3 bond of the pyrone ring leading to the formation of the double bond, as observed in other coumarin derivatives [16-17].

In the crystal structure, the flat chromene ring system (r.m.s deviation = 0.016 Å), formed by the coupling of benzene and 3,6-dihydro-2H-pyran rings, is positioned at a dihedral angle of 51.4(2)° relative to the benzoate-benzene ring. Additionally, the intramolecular C16—H16…O3 and C9—H9…O4 hydrogen bonds (Table 2.) give rise to an S(5) and S(6) ring motifs [18] which produces a pseudo-pentacyclic ring system illustrated in Figure 6.

Table 2. Hydrogen-bond geometry (Å, °)

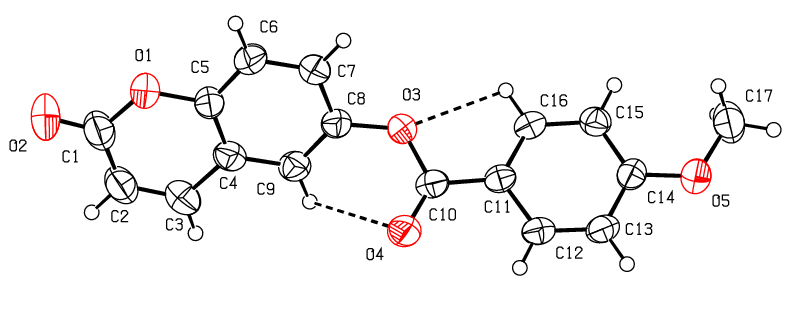Figure 6. An ORTEP [9] view of the title compound with the atomic numbering scheme. Displacement ellipsoids are shown at the 50% probability level. Dashed lines indicate hydrogen bonds

3.2.3. Supramolecular Features

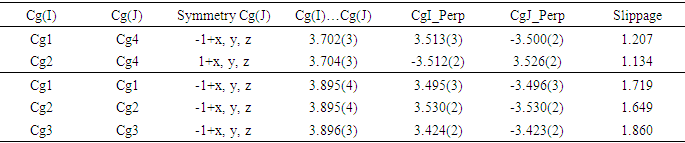
In the crystal structure, intermolecular C—H…O hydrogen bonds connect molecules into the a-axis direction (see Figure 7). Besides, there are intermolecular short contacts, including [O2…H17A(-1+x,y,-1+z) = 2.63 Å], [O2…H3(-x,-1/2+y,-z) = 2.64 Å], [H12…C16 (2-x,1/2+y,1-z) = 2.84 Å], [H12…C15 (2-x,1/2+y,1-z) = 2.84 Å] and [H9…O4(-1+x,y,z) = 2. 59 Å], which are closer together than the sum of their van der Waals radii.

Adding the above interactions to the π-π stacking interactions between the coumarin ring system and the C4-C9 benzene or pyrone rings led to the formation of the supramolecular aggregation shown in Figure 8. The distances between centroids, Cg1…Cg4 (-1+x, y, z) = 3.702 (3) and Cg2…Cg4 (1+x, y, z) = 3. 704 (3) Å, where Cg1, Cg2 and Cg4 correspond to the centroids of the pyrone, C4–C9 benzene and coumarin rings, respectively, are less than 3.8 Å, the maximum regarded as suitable for an effective π–π stacking interaction [19]. However, some interactions with centroid-centroid distances slightly above 3.8 Å are also retained (table 3). All these intermolecular interactions provide stability to the assembly of the three-dimensional crystal frameworks. The perpendicular distances of Cg(I) on ring J and distances between Cg(I) and perpendicular projection of Cg(J) on ring I (slippage) are summarized in Table 3.

Table 3. Analysis of short ring interactions (Å). Cg1, Cg2, Cg3 and Cg4 are the centroids of the pyrone, C4–C9, C11-C15 and chromene rings, respectively. The perpendicular distances of Cg(I) on ring J and distances between Cg(I) and perpendicular projection of Cg(J) on ring I (slippage) are reported

Table 4. Fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters (Å2)

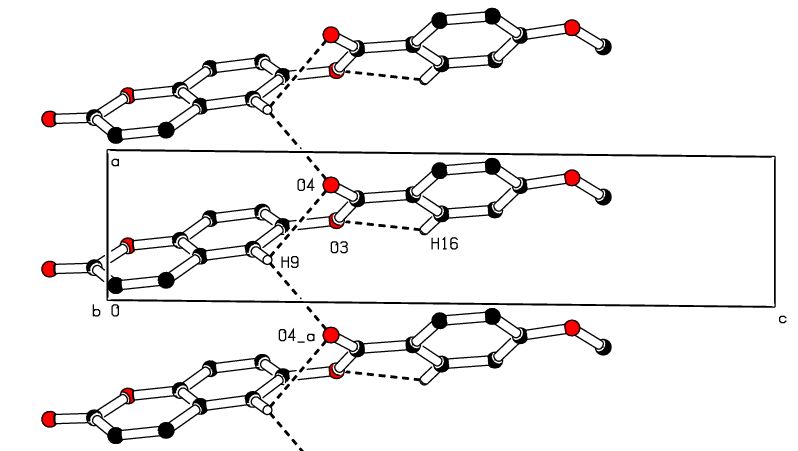Figure 7. Part of the crystal packing of the title compound showing the infinite 1D chain along [100]. Dashed lines indicate hydrogen bonds. H atoms not involved in hydrogen bonding have been omitted for clarity.

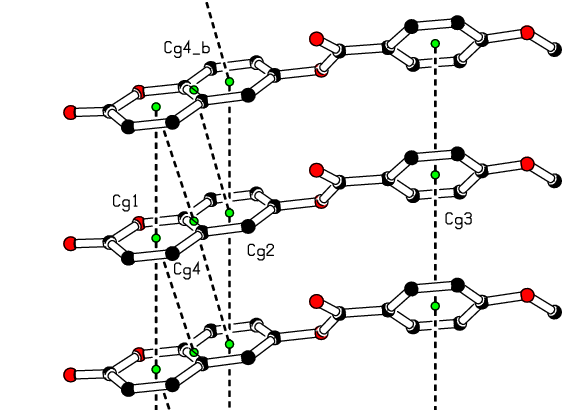Figure 8. A view of the crystal packing showing π–π stacking interactions (dashed lines). The green dots are ring centroids of rings

3.3. Hirshfeld Surface Analysis

In order to provide a complete analysis of the interactions between the molecules, compound (I) was subjected to a Hirshfeld surface analysis generated with CrystalExplorer 3.1. The 3D d_norm surface was calculated at standard (high) surface resolution and mapped with a color scale ranging from -0.117 (red) to 1.324 a.u. (blue). In (I), six bright red spots were observed on the d_norm map, indicating negative d_norm values that reflect distances shorter than the sum of the van der Waals radii. These red spots indicate predominant intermolecular C—H....O hydrogen bonds and short intermolecular contacts. Similarly, the shape index map, plotted from -1.00 to 1.00 a.u., highlights concave regions consisting of adjacent red and blue triangle-shaped spots that suggest π-π stacking interactions [20]. The mapping also displays white spots at distances equivalent to the sum of the van der Waals radii, and blue regions that exceed the sum of the van der Waals radii. Transparent surfaces are used to enhance visualization of the molecule (see Figures 9a, 9b and 9c). In addition, Figure 10 provides a decomposition of the two-dimensional fingerprint plots (FP) to highlight specific close contacts between atom pairs and their respective contributions. The blue spots occurring in the center of the surface at nearby de = di ≃ 1.8 Å signpost close C...C interplanar contacts. These contacts are linked to π–π stacking interactions and account for 10.4 % of the total Hirshfeld surface area (323.79 Ų), as shown in Figure 10a and predicted by the X-ray study. The main contribution to the Hirshfeld surface (34.9 %) is from H…O/O…H contacts which are depicted as blue spikes on the left side with the tip at de + di = 2.6 Å, top and bottom on the left side (Figure 10b), indicates the existence of O…H contacts.

As planned in organic compounds, the H...H contacts are great with a 33.3% contribution to the Hirshfeld surface area. These are positioned in the central area of the FP, with a blue peak in the center at de = di = 1.20 Å (see Figure 10c). In addition, the C…H/H…C plot (16.0 %) provides information on intermolecular C…H contacts (Figure 10d). Also, Figures 10e and 10f show C…O/O…C and O…O contacts in the FP with weak contributions to the Hirshfeld surface (4.4% for C…O/O…C and 1.0 % for O…O).

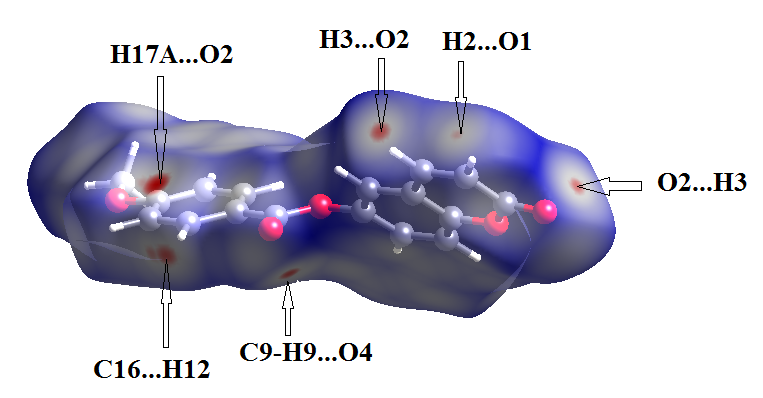Figure 9a. Hirshfeld surfaces mapped over dnorm (-0.117 to 1.324 a.u.)

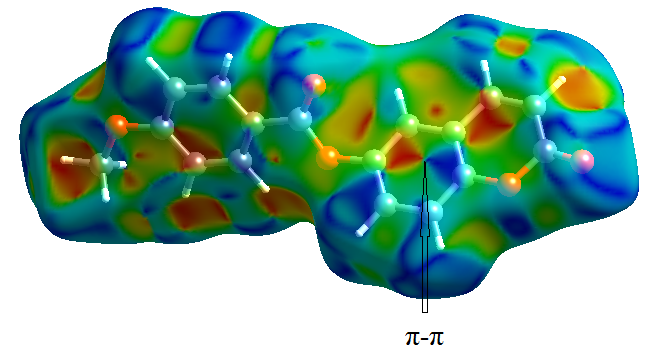Figure 9b. Shape-index map (-1.000 to 1.000 a.u)

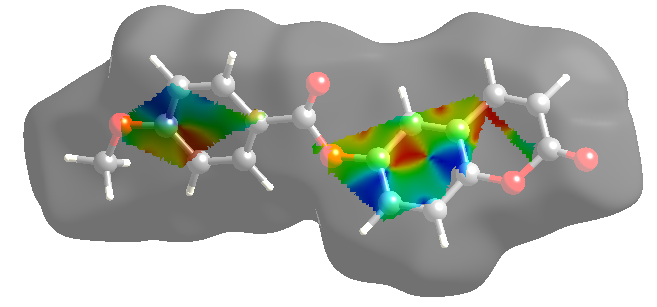Figure 9c. 2D plot showing the exact location of π–π stacking interactions

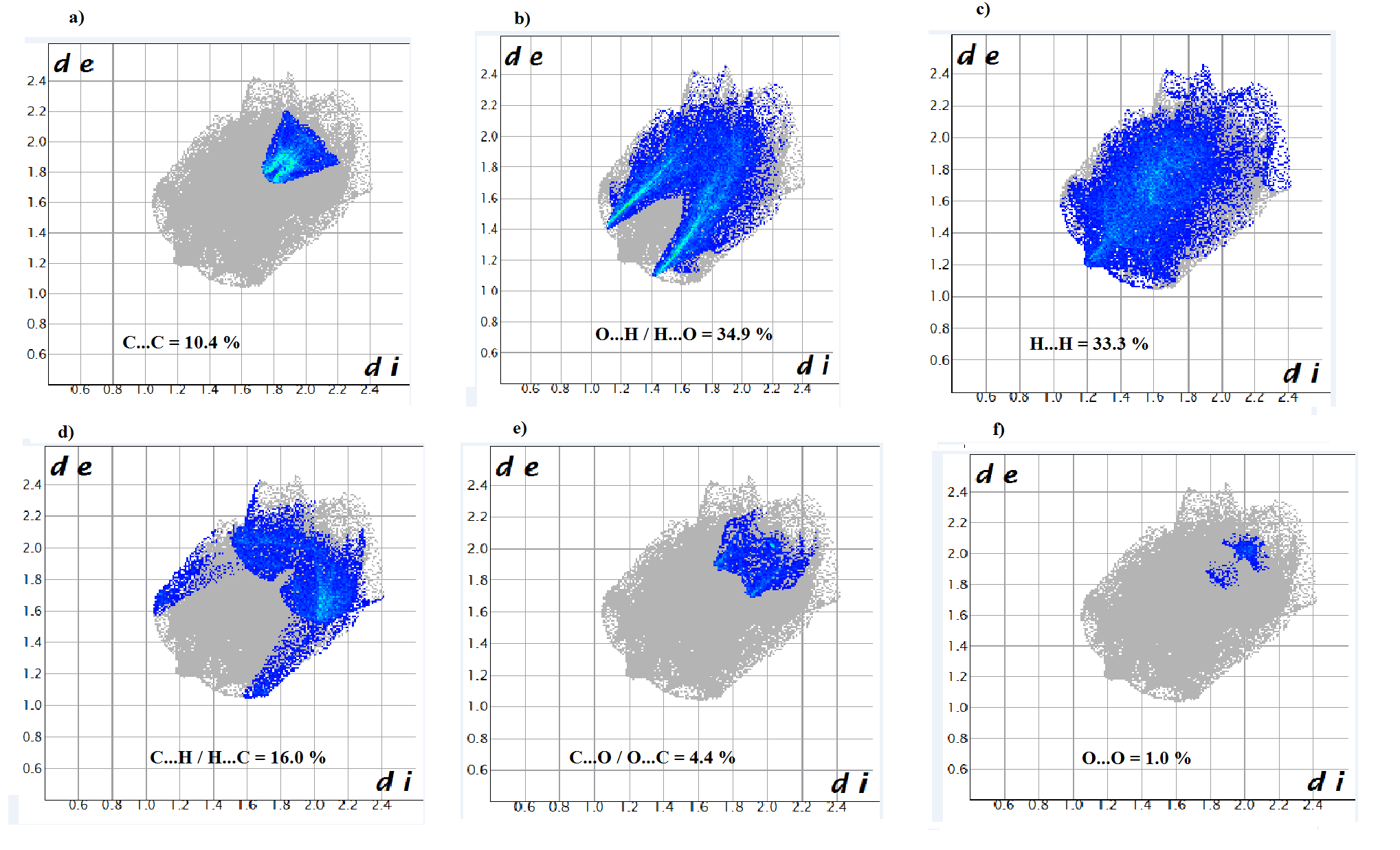Figure 10. Decomposed two-dimensional fingerprint plots for the title compound. Various close contacts and their relative contributions are indicated

3.4. Theoretical Calculations

3.4.1. Comparison of Geometrical Parameters and Vibrational Frequencies

Three methods were utilized to compare crystallographic (XRD) and computed structures. The first two approaches are used to compare geometric parameters, while the third is reserved for comparing spectra.

3.4.1.1. Comparison of Geometrical Parameters

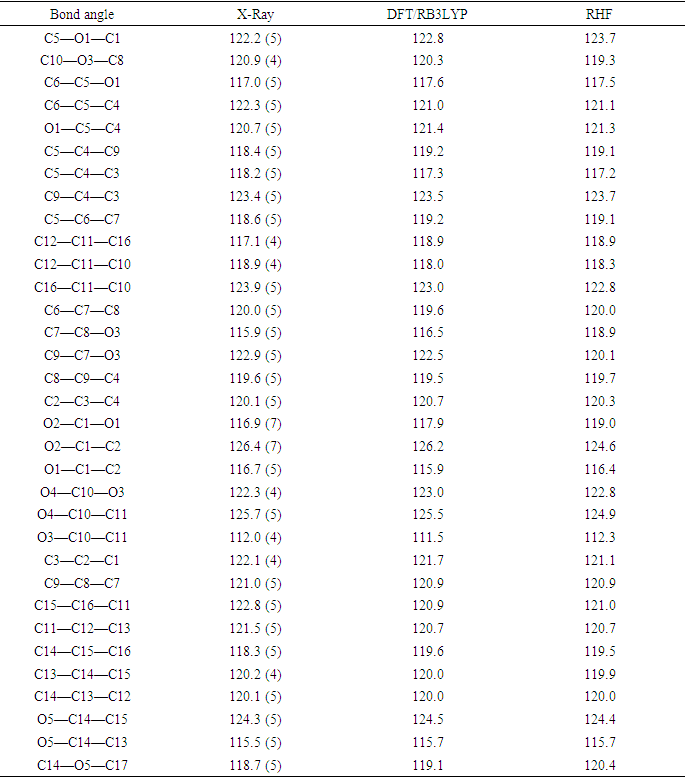
The first approach involved comparing the geometrical parameters from quantum computations to those acquired from the X-ray crystallographic study. Analyzing the computational bond lengths and angles and aligning them with the crystallographic outcomes displays a considerable accordance between them, evidenced by a root-mean-square deviation of 0. 014 Å (DFT/RB3LYP) and 0.016 Å (RHF) for bond lengths, and 0.8° (DFT/RB3LYP) and 1.2° (RHF) for bond angles (Tables 5 and 6).

Table 5. Experimental and calculated bond lengths in (Å) with 6-311++G(d,p) basis set

Table 6. Experimental and calculated bond angles (°) with 6-311++G(d,p) basis set

Furthermore, the correlation coefficients also confirm this trend, demonstrated by the high correlation coefficients of 0.96 and 0.93 for experimental vs calculated bond lengths and experimental vs calculated bond angles respectively for DFT/B3LYP calculations as well as 0.95 and 0.85 for RHF statistic models. Also, it was observed that the calculated torsion angles indicate planarity in the coumarin ring system, which aligns well with the crystallographic prediction as shown in Table 7. These theoretical calculations show that the results of the DFT calculations match the experimental (XRD) results better than the RHF outcomes.

Table 7. Experimental and calculated torsion angles (°)

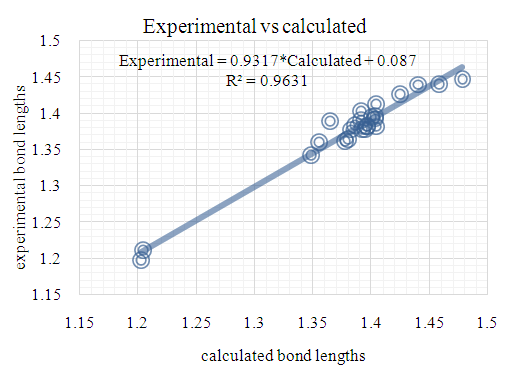Figure 11. DFT/B3LYP correlation graphic between the experimental and theoretical bond lengths in (Å)

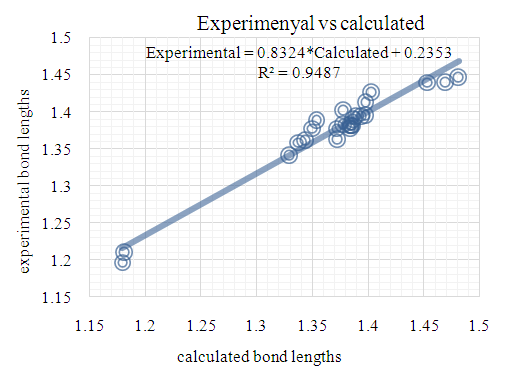Figure 12. RHF correlation graphic between the experimental and theoretical bond lengths in (Å)

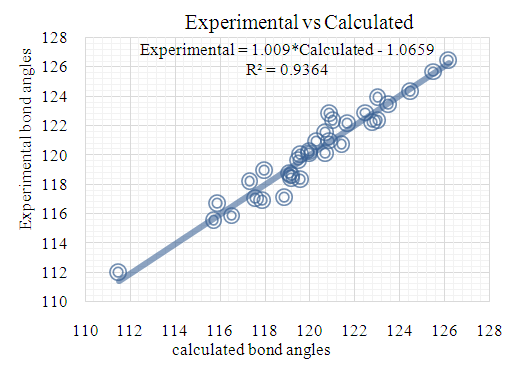Figure 13. DFT/B3LYP correlation graphic between the experimental and theoretical bond angles in (°)

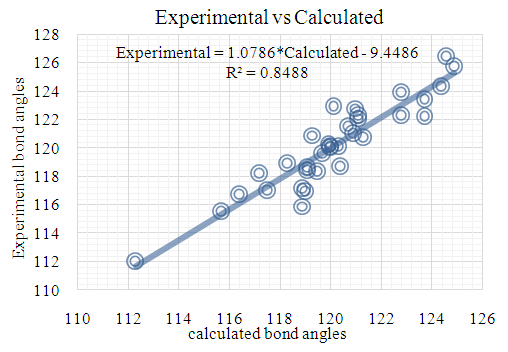Figure 14. RHF correlation graphic between the experimental and theoretical bond angles in (°)

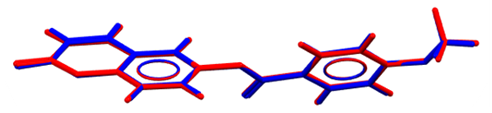Figure 15. Atom-by-atom superimposition of the X-ray structure (blue) on the calculated structure of (I), red, by (DFT/ B3LYP/6-311++G(d,p)

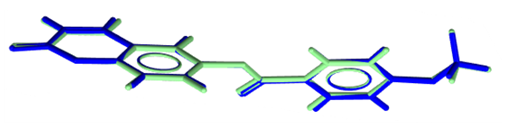Figure 16. Atom-by-atom superimposition of the X-ray structure (blue) on the calculated structure of (I), green, by RHF/6-311++G(d,p)

The second approach is to overlay the molecule derived from X-ray crystallography and that obtained from quantum chemical calculations using Mercury software [21]. Table 8 summarizes the RMSD for the overlay and the maximum distance between two equivalent atoms (Max. D).

Table 8, Figures 15 and 16 demonstrate that both model's calculated structures accurately match that of the XRD structure. Nevertheless, the DFT/B3LYP model shows better agreement than the HF model, a trend that is also observed in the first approach.

Table 8. Atom-by-atom superimposition results

Additionally, the examination of the torsion angles reveals the flat conformation of the coumarin ring system, which is consistent with the crystallographic prediction. However, a small discrepancy is noticeable in the torsion angle within the HF model, where the C10—O3—C8—C9 dihedral angle observed between this ring system and the benzoate ring (-51.3 (8)°) is somewhat lower than the computed value (-85.6°), (Table 7).

3.4.1.2. Comparison of Experimental and Computed Infrared Spectra

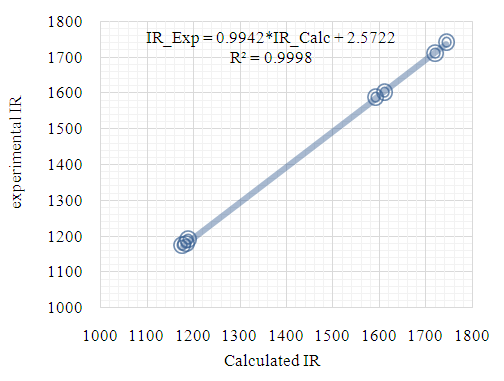Figure 17. Correlation graphic between the experimental and theoretical DFT vibration frequencies (cm–1)

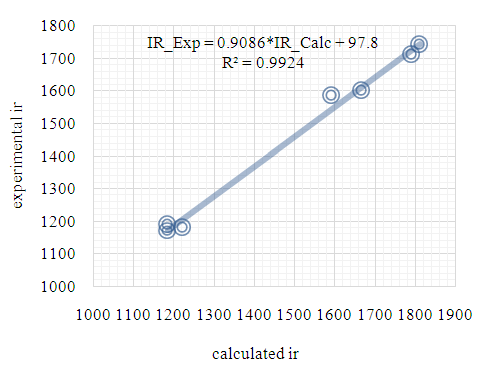Figure 18. Correlation graphic between the experimental and theoretical HF vibration frequencies (cm–1)

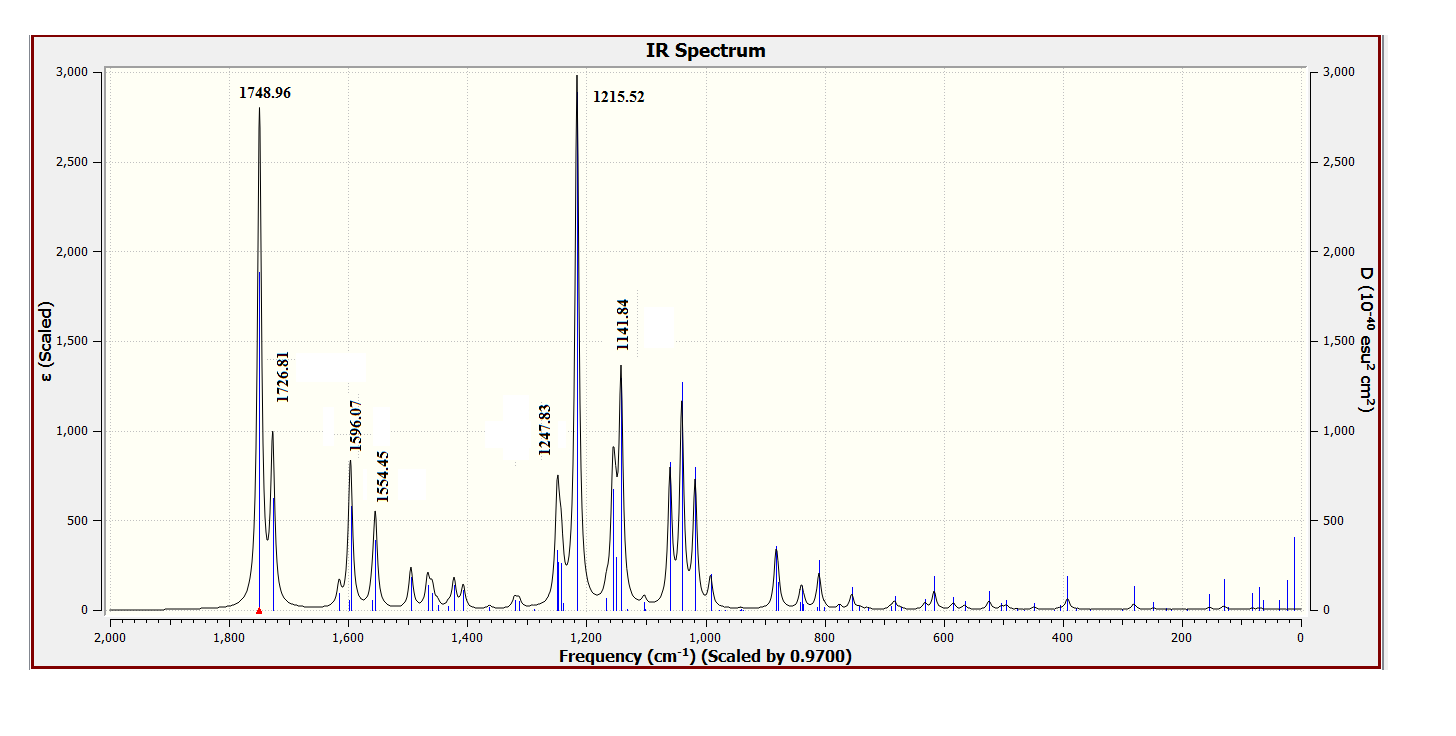Figure 19. DFT Calculated vibrational spectra of compound (I)

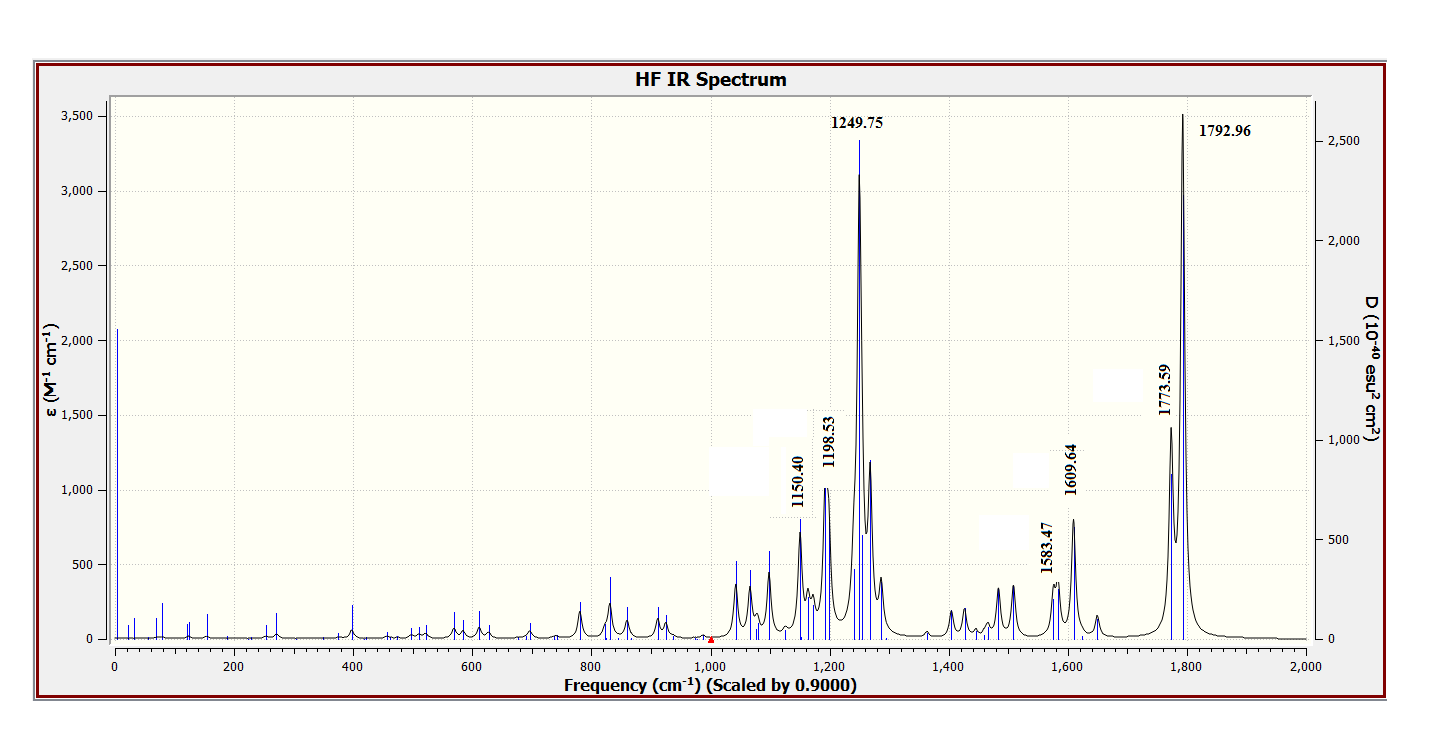Figure 20. DFT Calculated vibrational spectra of compound (I)

As third approach of comparison, we have computed the theoretical infrared spectra with frequency calculations utilizing DFT/B3LYP and HF methods. Some vibrational modes assigned by the Avogadro software [22] are listed in Table 9 alongside their corresponding experimental values. We conducted statistical models as linear regression between experimental and theoretical scaled frequencies that yield correlation R² values of 0.999 for DFT/B3LYP and 0.992 for HF models (Figures 17 and 18). These R² values close to unity demonstrate that the linear model developed here are appropriate for accurately estimating experimental infrared frequencies.

Table 9. Comparison of the observed and calculated stretching vibrational spectra of compound (I)

3.4.2. Molecular Electrostatic Potential (MEP)

The molecular electrostatic potential (MEP) is a useful property for examining the reactivity of various compounds and species. This property can be observed physically and measured experimentally using diffraction methods [23-24]. Additionally, computational methods can be employed to investigate MEP, thereby providing insight into various species' reactivity through wide-ranging electronic and nuclear charge distribution [25].

For ease of use, potential V(r) is commonly expressed in atomic units (a.u.), taking on the following form [26]:

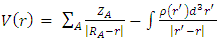(1)

Where 𝑍_𝐴 represents the charge of nucleus A situated at 𝑅_𝐴, 𝜌(𝑟’) refers to the electron density function of the molecule, and 𝑟’ is the dummy integration variable.

To identify the electrophilic and nucleophilic regions, MEP was calculated using the DFT/RB3LYP and RHF optimized geometries. The calculations were performed with the 6-311⁺⁺G(d,p) basis set for both methods. The results were then illustrated with color visualizations in Figure 14. In this figure, the red color indicates regions with a higher negative potential, which facilitate electrophilic attacks. Conversely, the blue color designates areas with higher positive potential that are conducive to nucleophilic attack.

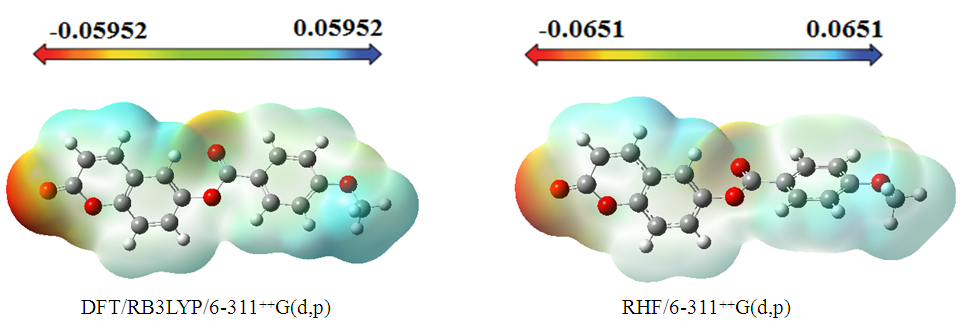Figure 21. MEP map (in atomic units) calculated using DFT/RB3LYP/6-311++G(d,p) and RHF/6-311++G(d,p)

Figure 21 shows that compound (I) has two potential sites for electrophilic attack. These negative regions are found about the oxygen atoms O2 and O4 for both methods. The maximum values for these negative regions are -0.05952 and -0.0651a.u. for DFT/RB3LYP/6-311⁺⁺G(d,p) and RHF/6-311⁺⁺G(d,p), respectively. Consequently, Figure 21 validates the occurrence of the intermolecular C9—H9…O4 interplay observed in the crystallographic study, i.e in the solid state.

3.4.3. HOMO-LUMO Analysis

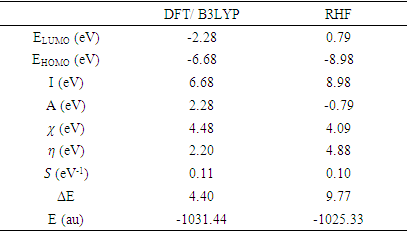
The energy levels and distributions of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of (I) are depicted in Figure 22. The calculations were carried out at both DFT/RB3LYP/6-311⁺⁺G(d,p) and RHF/6-311⁺⁺G(d,p) methods. The results indicate that the title compound possesses 77 occupied molecular orbitals, with the respective energy separation between LUMO and HOMO equaling to 4.40 and 9.76 eV. The orbital gaps, ranging from 4.40-9.76 eV, indicate that 2-oxo-2H-chromen-6-yl 4-methoxybenzoate is stable and less chemical reactive and is also called hard molecule [27], as also evidenced by the absence of imaginary frequencies in the results of both theoretical calculations. The computational results for compound (I), i.e. optimization, HOMO and LUMO energies are presented in Table 10 along with energy gap (Δ𝐸), ionization potential (𝐼), electron affinity (𝐴), absolute electronegativity (𝜒), absolute hardness (𝜂) and softness (𝑆). All parameters added to the table 10 have been estimated by using the following formulas utilizing the HOMO and LUMO energies of the molecule [28].

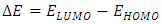(2)

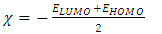(3)

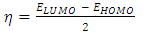(4)

(5)

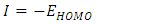(6)

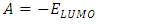(7)

Table 10. The calculated chemical properties of the title compound using DFT/RB3LYP/6-311++G(d,p) and RHF/6-311++G(d,p) levels

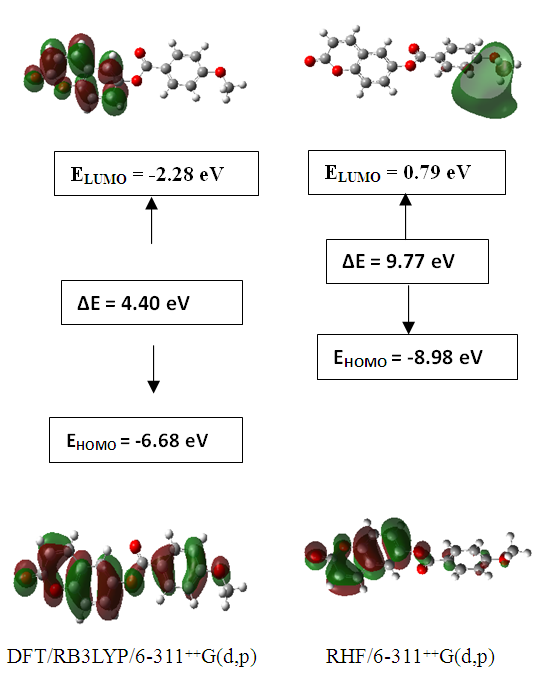Figure 22. The distributions and energy levels of the HOMO and LUMO orbitals computed for compound (I)

3.4.4. The Mulliken Charge Population

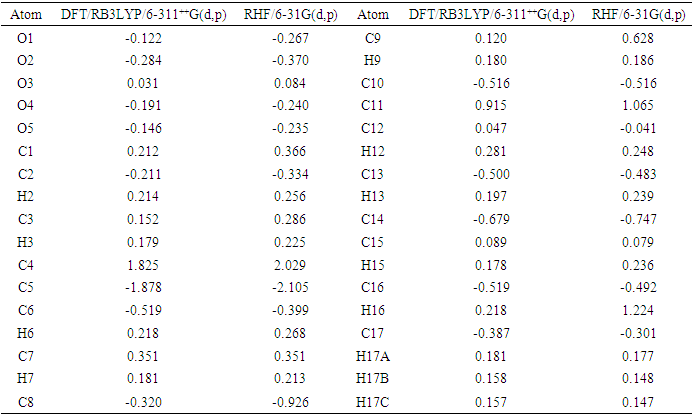
The Mulliken atomic charge calculation is vital in the application of quantum chemical computations to molecular systems, as atomic charges affect properties such as dipole moment, molecular polarizability, and electronic structure. The distributions for the equilibrium geometry of the title compound calculated by the Mulliken method [29-32] are presented in Table 11. Analysis of data from table 11 highlight that the intermolecular contacts are governed by electrostatic interactions. Indeed, the electrostatic force causes intermolecular contact between partially charged atoms of opposite signs, such as the pair of atoms (O2, H17A) with charges (-0.284 e, 0.181e) for the DFT model and (-0.370 e, 0.177e) for the HF model, leading to the interaction O2...H17A. The same applies to (H9, O4) with (0.180 e, -0.191 e) and (0.186 e, -0.240 e), (O2, H3) with (-0.284 e, 0.179 e) and (-0.370 e, 0.225 e) and (H12, C16) with (0.281 e, -0.519 e) and 0.248 e, -0.492 e), respectively, generate H9…O4, O2…H3 and H12…C16 interactions.

Table 11. Mulliken atomic charges computed

3.4.5. Non Linear Optical Properties

Nonlinear optical (NLO) effects occur when electromagnetic fields interact with different media, resulting in new fields that have altered phase, frequency, amplitude, or other propagation characteristics compared to the incident fields [33]. Avoiding excessive jargon and complex sentences, this definition is clear, concise, and objective. In recent years, the potential applications of new materials exhibiting efficient nonlinear optical (NLO) properties have generated significant interest for their use in modern communication technology, data storage, telecommunications, and optical signal processing. Numerous research papers have been published on this topic [34-38]. The current expectation is that utilizing quantum chemical methods such as Hartree-Fock (HF) and density functional theory (DFT) for molecular hyperpolarizabilities will provide supervision and hasten subsequent experimental studies [39-40].

Thus, in this study, we calculated the dipole moments (μ), polarizabilities (<α>), anisotropy of polarizabilities (<Δα>), and first-order hyperpolarizabilities (β), which indicate the material's ability to generate second-order non-linear effects [41]. The calculations were performed at RHF and DFT/RB3LYP optimized geometries using the GAUSSIAN-09W program package [14] and the 6-311⁺⁺G(d,p) basis set. These parameters are defined as [42-43].

(8)

(9)

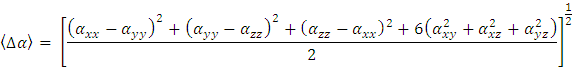(10)

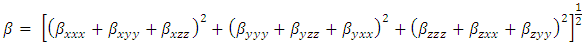(11)

The tensors' numerical outcomes for polarizability have been converted to electronic units (esu) and presented into tables 12, 13, and 14. The conversion rate is (α: 1a.u. = 0.1482 x10^-24 esu; β: 1a.u.= 8.6393x10^-33 esu) [44].

Table 12. Computation results for the dipole moment (D)

Table 13. All α ×10−24 (esu) components, <α> ×10−24 (esu) and <Δα> ×10−24 (esu) values calculated using HF and DFT levels of theory

Table 14. All β (a.u.) components and β ×10−30 (esu) values calculated using HF and DFT levels of theory

For investigation, urea is a commonly used molecule for evaluating NLO effects in molecular systems. It serves as a benchmark for NLO parameters. Compound (I) exhibits larger parameter values than urea, as shown by the values of all parameters (<µ > = 1.37D, <α> = 3.83x10^-24 esu [45-47], and <β > = 0.1947x10^-30 esu [48]).

For further information, the dipole moment of compound (I) were calculated at 5.81 and 5.88 times grander than those of the urea molecule for DFT/B3LYP and HF calculations, respectively (Table 12). Additionally, the first-order hyperpolarizabilities of the studied compound were calculated (Table 14) and were 26.30 and 25.99 times larger than that of the urea molecule for DFT/B3LYP and HF calculations, respectively. Furthermore, the calculated values for the average linear polarizability <α> are 9.06 (DFT/B3LYP) and 7.87 (HF) times higher than that of the urea molecule, respectively, as indicated in Table 13. This comparison demonstrates that 2-oxo-2H-chromen-6-yl 4-methoxybenzoate exhibits a high first-order hyperpolarizability, suggesting that it may be suitable for NLO experience.

5. Conclusions

The molecular structure was examined in this study using Spectrometry and X-ray crystallography. Intermolecular interactions were also analyzed through Hirshfeld surface analysis.

Additionally, molecular electrostatic potential, HOMO-LUMO analysis, Mulliken charge populations, and nonlinear optical properties of 2-oxo-2H-chromen-6-yl 4-methoxybenzoate were investigated utilizing DFT/RB3LYP/6-311⁺⁺G(d,p) and RHF/6-311⁺⁺G(d,p) calculations. The computed geometric parameters, including bond length, bond angle, torsion angle, and infrared spectrum, are compared to their corresponding experimental data. The comparison reveals no significant differences between the experimental and theoretical structures, except for the experimental torsion angle, C10—O3—C8—C9, which differs from the RHF calculated value. The MEP maps indicate that negative potential sites reside on electronegative atoms, and positive potential sites are found around the hydrogen atoms. This information reveals the areas where intra- and intermolecular interactions can occur. Additionally, the Mulliken charges in the solid state can confirm or refute the C9-H9...O4 intermolecular hydrogen bonds and some short interactions in the structure. Besides, the compound's calculated average linear polarizability value using DFT/B3LYP and HF methods shows nonlinear optical properties for compound (I).

ACKNOWLEDGEMENTS

The authors thank the Spectropole Service of the Federation of Chemical Sciences at Aix-Marseille University in France for conducting the complete analysis.