-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Organic Chemistry
p-ISSN: 2163-1271 e-ISSN: 2163-1301
2012; 2(2): 21-25
doi: 10.5923/j.ajoc.20120202.04
Oxidation of L-Valine by Manganese(III) in Pyrophosphate Medium: Kinetics and Mechanism
C. S. Chidan Kumar 1, S. Chandraju 2, Netkal M. Made Gowda 3
1Department of Chemistry, G. MadeGowda Institute of Technology, Bharathi Nagar 571422, Mandya, Karnataka, India
2Department of Studies in Sugar Technology, Sir M. Visweswarayya Post-Graduate Center, University of Mysore, Tubinakere 571402, Mandya, Karnataka, India
3Department of Chemistry, Western Illinois University, One University Circle, Macomb, IL 61455, USA
Correspondence to: S. Chandraju , Department of Studies in Sugar Technology, Sir M. Visweswarayya Post-Graduate Center, University of Mysore, Tubinakere 571402, Mandya, Karnataka, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Kinetics of oxidation of L-valine (Val) by manganese(III) pyrophosphate has been studied as a function of pH (0.94-1.90) at 313 K. The reaction shows a first-order dependence of rate each on [Mn(III)] and [Val], a fractional-order on [H+], and an inverse fractional-order each on [Na4P2O7] and [Mn(II)]. Effects on the rate of anions, such as [F-], [Cl-] and [ClO4-], and the dielectric constant of the solvent medium have been studied. Solvent isotope studies have been performed in D 2O medium. Activation parameters have been determined from Arrhenius and Eyring plots. A mechanism consistent with the observed kinetics is proposed and discussed.
Keywords: Kinetics, manganese(III), valine, oxidation, reduction, mechanism, rate law
Article Outline
1. Introduction
- Studies of oxidation of organic substrates such as amino acids by transition metal ions of higher oxidation states in solution have received considerable attention. of these, manganese(III) oxidations are of special importance because of their biological relevance[1]. Manganese-porphyrins have been studied as possible models for closely related and biologically significant systems[2]. Several studies have been reported on the kinetics oxidations of substrates by manganese(III) in perchlorate, sulfate, and acetate media[3]. As a part of our investigations on the redox reactions of transition metal compounds [4-10], we report herein the kinetics of oxidation of L-valine by manganese(III) pyrophosphate.
2. Experimental
- MaterialsStock solutions of manganese(III) pyrophosphate ( 0.05 M at pH 5.0) were prepared by the standard method of Belcher and West[11]. The pH of the solution was varied by adding the required amount of phosphoric acid or sodium pyrophosphate. Chromatographically pure sample of L-valine (Sisco Research Laboratories, India) was further assayed by standard methods[12]. Aqueous stock solution of Val (0.400 M) was freshly prepared and used, whenever needed. All other chemicals used were of analytical grade. Triply distilled water was employed for preparing all aqueous solutions.
2.1. Kinetic Procedure
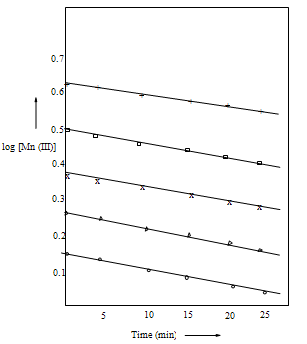
- The kinetic studies were made in glass-stoppered Pyrex tubes under pseudo-first order conditions of [substrate] >> [Mn(III)]. Each reaction mixture consisted of solutions of Val, the acid (phosphoric acid to maintain acid concentration), the salt (sodium pyrophosphate to maintain constant ionic strength), manganese(II). Water was added to keep the total volume constant and the mixture was thermally equilibrated at constant temperature (e.g., 313 K). A known amount of the standard manganese(III) pyrophosphate stock solution maintained at the same temperature was added and mixed thoroughly to initiate the reaction. The progress of the reaction was monitored for at least two half-lives by iodometric determination of the unreacted Mn(III) at regular intervals of time. The pseudo-first order rate constants (k′ or kobs) obtained by a graphical method of plotting log (Mn(III) titer value) vs. time were found to be reproducible within ± 5% error.
2.2. Preliminary Studies
- The maximum absorption wavelength of manganese(III) pyrophosphate solution at pH 5.0 occurs at 500 nm which on variation of pH shifts significantly along with a change in molar absorptivity (Fig. 1). The formal redox potential (Eo1) of the Mn(III)-Mn(II) couple was measured by the usual method of mixing different proportions of air-free oxidized and reduced forms of manganese ion solutions containing an overall 0.50 M pyrophosphate in the pH range 0.70-3.0. The values of E(V vs SCE) are 1.090, 1.218, 1.231,1.259, 1.289 and 1.307 V at pH values of 2.9, 1.65, 1.53, 1.33. 1.01 and 0.70, respectively, which are consistent with the literature data [6-10].
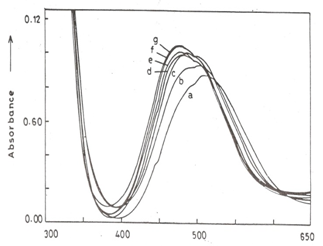 | Figure 1. Absorption spectra of 1.00 X 10-3 M Mn(III) in pyrophosphate solutions. pH=0.31(a); 1.85(b); 2.9(c); 3.9(d); 5.20(e); 6.26(f); and 8.09 (g) |
2.3. Reaction Stoichiometry and Product Analysis
- The following 2:1 stochiometry was observed, with reaction mixtures of [Mn(III)] > [Val] studied for various time periods up to 48 h:
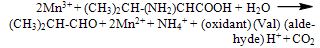 | (1) |
2.4. Test Free Radicals
- The reaction mixtures of Val and Mn(III) were tested for the presence of free radicals using monomers, acrylonitrile and methyl methacrylate (10% solution)[14-17]. The addition of the monomer to the reaction mixture, after it was purged with nitrogen, in the dark resulted in the precipitation of a polymer product. This positive response indicated the in situ generation of free radicals in the reaction mixture. Control experiments with the solutions of Mn(III), Mn(II), and Val were also performed under the same experimental conditions, which did not show any precipitation.
3. Results
3.1. Dependence of the Rate on [Mn(III)] and [Val]
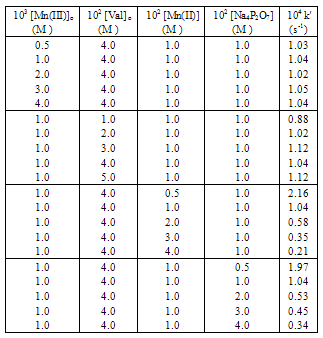
- In the Mn(III) oxidation of valine, the effect on the reaction rate was investigated by varying either [Mn(III)]o or [Val]o at constant pH and temperature. The linearity of the pseudo-first order plots of log [Mn(III)] or titer value) vs. time showed the first–order dependence of the reaction rate on [Mn(III)], which was monitored in the reaction (Table 1, Fig. 2). The increase in the [Val]o increased the rate constant at constant pH and other conditions (Table 1). A linear plot of log k′ or vs. log [Val]o with a unit slope showed the first– order dependence of the rate on [Val].
|
3.2. Dependence of the Rate on pH
- The reaction rate increased with a decrease in pH and a plot of log k′ vs. pH was linear (Fig. 3) with a negative slope of -0.53, indicating a positive fractional-order dependence of the rate on [H+].
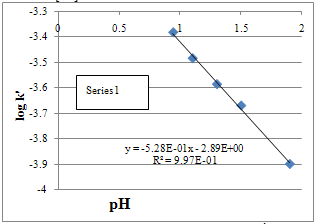 | Figure 3. Plot of log k’ vs. –log [H+]. [Mn(III)] o = 1.00 X 10-3 M; [Val] o = 4.00 X 10 -2M; [Mn(II)] = 1.00 x10-2 M; [Na4P2O7]=1.00 X10 -2M; T=313 K |
3.3. Dependence of the Rate on Ionic Strength
- The rate decreased with an increase in the [Na4P2O7] leading to a linear plot of log k′ vs. log [Na4P2O7] with a negative slope, showing an inverse fractional-order dependence of the rate on [Na4P2O7].
3.4. Dependence of Rate on [Mn(II)] and Salts
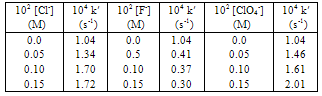
- An increase in the concentration of the reduction product, Mn(II), decreased the rate (Table 1) and a log-log plot gave a negative fractional-order in [Mn(II)]. Also, the effects of added sodium salts containing anions such as F-, Cl- and ClO4- on the rate of reaction were investigated (Table 3). Increase in [Cl-] and [ClO4-] increased the rate, while increase in [F-] decreased the rate. This effect is attributable to the replacement of the pyrophosphate ligand in the complex with other anions leading to the establishment of a new Mn(III)-Mn(II) redox couple involving ligands, F-, Cl- and ClO4-.
|
3.5. Effect of Solvent Composition or Dielectric Constant on the Reaction Rate
- The dependence of the reaction rate on dielectric constant (D) of the reaction medium was verified by studying the reaction at various percentages of EtOH in water. It was found that the rate decreased with an increase in the percentage of EtOH. In other words, the observed rate constant decreased with a decrease in D (Table 4). A plot of ln k′ vs. ln 1/D had a slope, which is consistent with the Amis concept for dipole-dipole or ion–dipole interactions[7].
3.6. Dependence of the Rate on Temperature
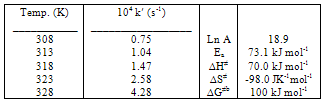
- The effect of temperature on the rate constant was determined by performing the reaction in the range, 308 K-328 K, at constant [Mn(III)], [Val], [Mn (II)], [P2O74-] and pH (Table 5). Arrhenius and Eyring13 plots of log k′ vs. 1/T and log (k′/T) vs. 1/T (Fig. 4), respectively, gave good straight lines. From the slopes and intercepts, the activation parameters were calculated as summarized in Table 5.
|
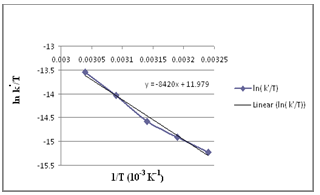 | Figure 4. Eyring plot |
3.7. Solvent Isotope Studies
- The reaction was studied in D2O medium (60%). Rate constants in H2O and D2O were found to be 1.04 x 10-4 s-1 and 2.1 x 10-4 s-1, respectively. These values lead to the solvent isotope effect17, k(H2O)/ (kD2O), of 0.51.
4. Discussion
4.1. Mechanism
- In acidic pH, chelating pyrophosphate ligand coordinates to manganese(II and III) to form chelates containing complex anions, Mn(H2P2O7)34- and Mn(H2P2O7)33-. Therefore, the oxidant Mn(III) is a complex species. The observed kinetic results of first-order each in [Mn(H2P2O7)3-3] and [Val], a fractional-order in [H+] and an inverse fractional-order in [Mn(H2P2O7)3-4] and [H2P2O7-2] can be supported by Scheme I below.
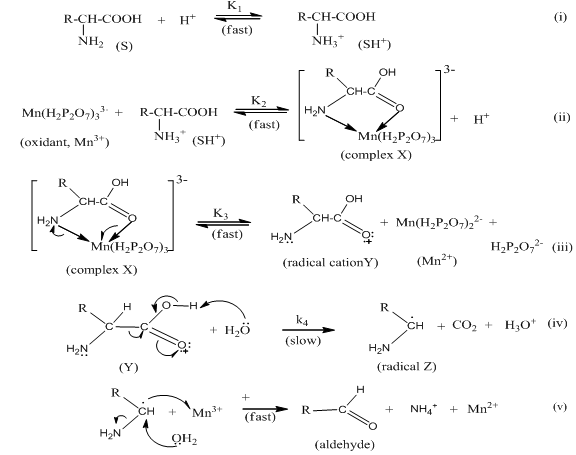 | Scheme 1. Mechanism of valine oxidation by Mn(III) in acid solutions |
4.2. Rate law Derivation
- The rate of oxidation is given by the slow step in Scheme I as,
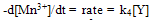 | (2) |
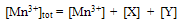 | (3) |
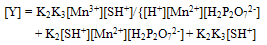 | (4) |
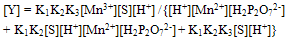 | (5) |
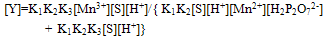 | (6) |
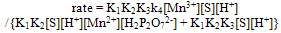 | (7) |
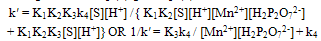 | (8) |
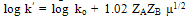 | (9) |
5. Conclusions
- The redox reaction of Val with Mn(III) pyrophosphate has been investigated in acid solutions. The reaction stoi- chiometry, involving the oxidation of Val to isobutyraldehyde and reduction of Mn(III) to Mn(II), has been found to be 1 mol Val : 2 mol Mn(III).The reaction shows the following experimental rate law: rate = k′ [Mn(III)] [Val] [H+]x /[Mn(II)]y [Na4P 2O 7]z, where x, y, and z represent fractional orders. A free radical mechanism (Scheme I) proposed is consistent with the experimental rate law. The activation parameters, Ea, ∆H≠, ∆G≠, and ∆S≠, have been determined to understand whether the reaction is controlled by entropy or enthalpy. The negative ∆S≠ indicates the rigid transition state formation with a loss of degrees of freedom and the entropy-controlled reaction.
References
| [1] | Boucher, J., 1972, Coord. Chem. Rev, 7, 289. |
| [2] | Calvin, M., 1965, Rev. Pure Appl. Chem., 15, 1. |
| [3] | Davies, G, 1969, Coord. Chem Rev., 4, 199 |
| [4] | Pinto, I., Sherigara, B. S., and Udupa, H.V. K., 1990, Bull. Chem. Soc. Japan, 63, 3625. |
| [5] | Ishwara Bhat, K., Sherigara, B.S., and Pinto, I., 1993, Trans. Met. Chem., 18, 163. |
| [6] | Chandraju, S., Sherigara, B. S., and Made Gowda, N. M., 1994, Int. J. Chem. Kinet., 26, 1105. |
| [7] | Sherigara, B. S., Ishwara Bhat, K., Pinto, I., and Made Gowda, N. M., 1995, Int. J. Chem. Kinet., 27, 675. |
| [8] | Rangappa, K. S., Chandraju, S., and Mahadevapa, D. S., 1996, Trans. Met. Chem., 21, 519. |
| [9] | (a) Sharigara, B. S., Ishwara Bhat, K., and Pinto, I., 1995, Amino Acids 8, 291; (b). Chidan Kumar, C. S., Chandraju, S., and Made Gowda, N.M., 2011 , Synthesis and Reactivity in Inorganic, Metal-Organic, and Nano-Metal Chemistry, 41(10), 1331-1337. |
| [10] | (a) Beg, M.A., and Kamaluddin, 1975, Indian J. Chem., 13, 1167; (b) Rangappa, K. S., Esterline, D. S., Mythily, C. K., Mahadevappa, D. S., and Ambekar, S. Y, 1993, Polyhedron, 12, 1719. |
| [11] | Belechur, R., and West, T. S., 1952, Anal. Chim. Acta, 6, 322. |
| [12] | A. I. Vogel, Qualitative Organic Analysis, London, U. K.: Longman and Green, 1958. |
| [13] | Laidler, K. J., and Eyring, H., 1940, Ann. New York Acad. Sci., 39, 303. |
| [14] | W. A. Waters, and J. S. Littler, Oxidation in Organic Chemistry, Wiberg, K.B., Ed. New York, U. S.: Academic Press, 1965, vol. 5a, pp.185-241. |
| [15] | C. J. Collins, and N.S. Bowmann, Isotope Effects in Chemical Reactions, New York, U. S.: Van Nostrand Reinhold Co., 1970 . |
| [16] | E. S. Amis, Solvent Effects on Reaction Rates and Mechanisms, New York, U. S.: Academic Press, 1966. |
| [17] | R. D. Gilliom, Introduction to Physical Organic Chemistry, London, U. K.: Addison – Wesley, 1970. |
| [18] | Varadarajan, R. and Joseph, M., 1980, Indian J. Chem., 19A, 1977. |
| [19] | Kamaluddin, 1980, Indian. J. Chem., 19A, 431-434. |
| [20] | Ramachandran, M. S., Vivekanadan, T. S., and Khadar, S S., 1984, Indian J. Chem., 23A, 379. |
| [21] | C. Richardt, Solvents and Solvent Effects in Organic Chemistry, 3rd edn, Wiley-Vett, New York, 2003. |
| [22] | A. Kohen and H. H. Limbach, Isotope Effects in Chemistry and Biology, CRC press, Boca Raton, Florida, 2006. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML