-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2022; 12(1): 5-8
doi:10.5923/j.ajms.20221201.02
Received: Feb. 16, 2022; Accepted: Mar. 4, 2022; Published: Mar. 15, 2022

Algebraic Points of Given Degree on the Affine Curve 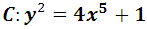
El Hadji Sow, Moussa Fall, Oumar Sall
U.F.R. of Science and Technology, Mathematics and Applications Laboratory, Assane SECK University of Ziguinchor, Senegal
Correspondence to: El Hadji Sow, U.F.R. of Science and Technology, Mathematics and Applications Laboratory, Assane SECK University of Ziguinchor, Senegal.
| Email: |  |
Copyright © 2022 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this work, we determine the set of algebraic points of given degree over 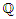 on the curve of affine equation
on the curve of affine equation 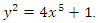 This note extends a result of Booker, Sijsling, Sutherland, Voight and Yasak in [1] who gave a description of the set of
This note extends a result of Booker, Sijsling, Sutherland, Voight and Yasak in [1] who gave a description of the set of 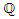 -rational points i.e the set of points of degree one over
-rational points i.e the set of points of degree one over  on this curve.
on this curve.
Keywords: Planes curves, Degree of algebraic points, Rationals points, Algebraic extensions, Jacobian
Cite this paper: El Hadji Sow, Moussa Fall, Oumar Sall, Algebraic Points of Given Degree on the Affine Curve 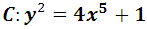 , American Journal of Mathematics and Statistics, Vol. 12 No. 1, 2022, pp. 5-8. doi: 10.5923/j.ajms.20221201.02.
, American Journal of Mathematics and Statistics, Vol. 12 No. 1, 2022, pp. 5-8. doi: 10.5923/j.ajms.20221201.02.
1. Introduction
- Let
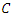 be a smooth algebraic curve defined over
be a smooth algebraic curve defined over  Let
Let 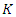 be a numbers field. We note by
be a numbers field. We note by 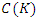 the set of points of
the set of points of 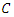 with coordinates in
with coordinates in 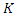 and
and 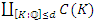 the set of points of
the set of points of 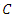 with coordinates in
with coordinates in 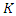 of degree at most
of degree at most 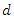 over
over  The goal is to determine the set of algebraic points of given degree over
The goal is to determine the set of algebraic points of given degree over  on the curve
on the curve 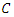 given by the affine equation
given by the affine equation 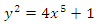 The Mordell-Weil group
The Mordell-Weil group 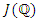 of rational points of the Jacobian is a finite set (refer to [1,4]).We denote by:
of rational points of the Jacobian is a finite set (refer to [1,4]).We denote by: 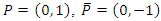 and
and 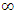 the point at infinity. In [1] Booker, Sijsling, Sutherland, Voight and Yasak gave a description of the rational points over
the point at infinity. In [1] Booker, Sijsling, Sutherland, Voight and Yasak gave a description of the rational points over 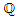 on this curve. This description is as follows:Proposition: The
on this curve. This description is as follows:Proposition: The  -rational points on
-rational points on 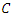 are given by
are given by 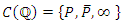 In this note, we give an explicit description of algebraic points of given degree over
In this note, we give an explicit description of algebraic points of given degree over  on the curve
on the curve 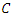 .Our main result is given by the following theorem:Theorem: The set of algebraic points of given degree over
.Our main result is given by the following theorem:Theorem: The set of algebraic points of given degree over  on the curve
on the curve 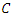 isgiven by:
isgiven by: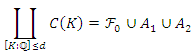 With:
With: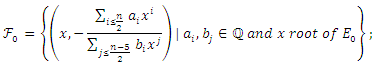
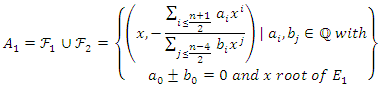 and
and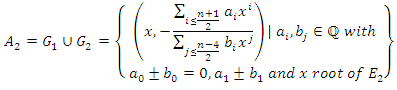 where
where 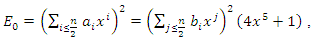
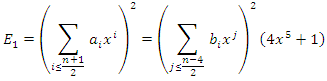 and
and 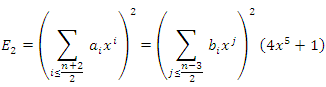
2. Auxiliary Results
- For a divisor
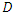 on
on 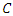 , we note
, we note 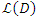 the
the  -vector space of rational functions
-vector space of rational functions 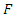 defined on
defined on  such that
such that 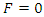 or
or 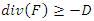 ;
; 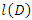 designates the
designates the 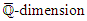 of
of 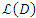 . In [1, 4] the Mordell-Weil group
. In [1, 4] the Mordell-Weil group 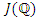 of
of 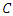 is isomorph to
is isomorph to 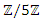 and
and 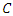 is a hyperelliptic curve of genus
is a hyperelliptic curve of genus 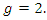 Let
Let 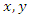 be two rational functions on
be two rational functions on 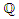 defined as follow:
defined as follow: 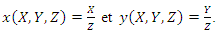 The projective equation of
The projective equation of 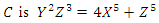 We denote by
We denote by 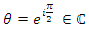 and let's put
and let's put 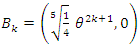 for
for 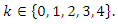 Let us designate by
Let us designate by 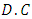 the intersection cycle of algebraic curve
the intersection cycle of algebraic curve 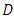 defined on
defined on  and
and 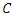 .Lemma 1:
.Lemma 1: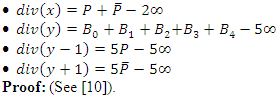 Consequence of lemma 1:
Consequence of lemma 1: 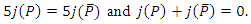 Lemma 2:
Lemma 2: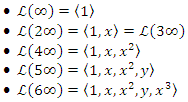 Proof:- We have
Proof:- We have 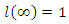 since if
since if 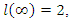 then the curve
then the curve 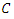 is of genus zero (see [1,4]), which is not the case.- Since the genus of
is of genus zero (see [1,4]), which is not the case.- Since the genus of 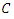 is equal to 2, then
is equal to 2, then 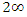 is a canonical divisor of
is a canonical divisor of 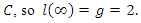 - For the rest we apply the Riemann-Roch theorem which says that
- For the rest we apply the Riemann-Roch theorem which says that 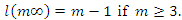 Lemma 3:A
Lemma 3:A 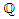 -base of
-base of 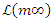 is given by
is given by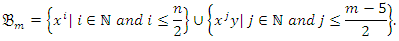 Proof: It is clear that
Proof: It is clear that 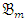 is free and it remains to show that
is free and it remains to show that 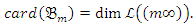 According to the Riemann-Roch theorem, we have
According to the Riemann-Roch theorem, we have 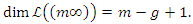 According to the parity of
According to the parity of 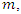 we have the following two cases:Case 1: Suppose that
we have the following two cases:Case 1: Suppose that 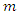 is even and let
is even and let 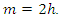 Thus we have
Thus we have 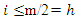 and we have
and we have 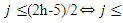
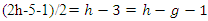 . Then we get
. Then we get 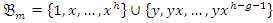 . we have
. we have 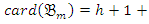
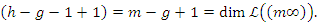 Case 2: Suppose that
Case 2: Suppose that 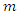 is odd and let
is odd and let 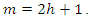 Thus we have
Thus we have 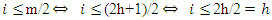 and
and 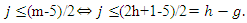 Then we get
Then we get 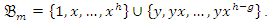 We have
We have 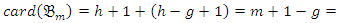
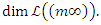 Lemma 4:
Lemma 4: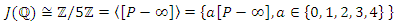 Proof: (See [1,4]).
Proof: (See [1,4]).3. Proof of Theorem
- Given
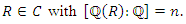 The work of Booker, Sijsling, Sutherland, Voight and Yasak in [1] allows us to assume that
The work of Booker, Sijsling, Sutherland, Voight and Yasak in [1] allows us to assume that 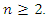 Note that
Note that 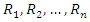 are the Galois conjugates of
are the Galois conjugates of 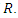 Let's work with
Let's work with 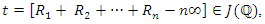 according to lemma 4 we have
according to lemma 4 we have 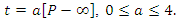 So we have
So we have 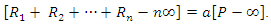 Our proof is divided in three cases:Case
Our proof is divided in three cases:Case 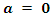 We have
We have 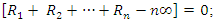 then there exist a function
then there exist a function 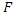 with coefficient in
with coefficient in  such that
such that 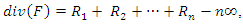 then
then 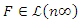 and according to lemma 3 we have
and according to lemma 3 we have 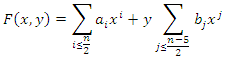 For the points
For the points 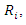 we have
we have 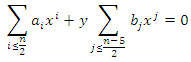 hence
hence 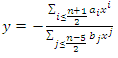 and the relation
and the relation 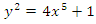 gives the equation
gives the equation 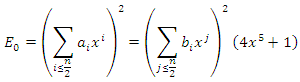 We find a family of points
We find a family of points 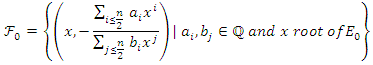 Cases
Cases 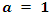 and
and 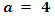 For
For 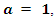 we have
we have 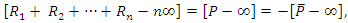 then there exist a function
then there exist a function 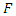 with coefficient in
with coefficient in  such that
such that 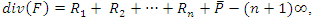 then
then 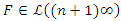 and according to lemma 3 we have
and according to lemma 3 we have 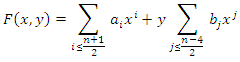 We have
We have 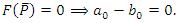 For the points
For the points 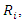 we have
we have 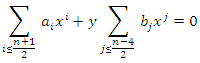 hence
hence 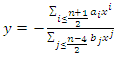 and the relation
and the relation 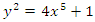 gives the equation
gives the equation 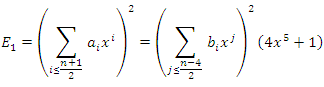 We find a family of points
We find a family of points 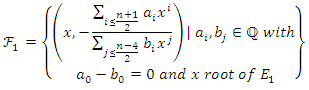 For
For 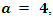 we have
we have 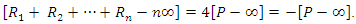 By a similar argument as in case
By a similar argument as in case 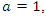 we have
we have 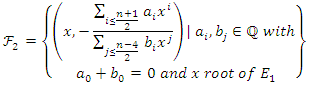 Finally, we have the family
Finally, we have the family 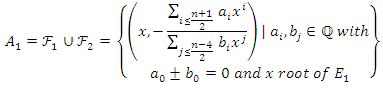 Cases
Cases 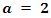 and
and 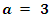 For
For 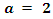 , we have
, we have 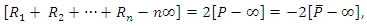 then there exist a function
then there exist a function 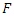 with coefficient in
with coefficient in 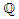 such that
such that 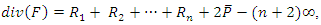 then
then 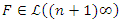 and according to lemma 3 we have
and according to lemma 3 we have 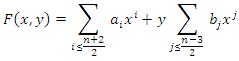 The function
The function 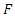 is of order 2 at point P so we must have
is of order 2 at point P so we must have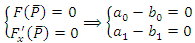 For the points
For the points 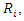 we have
we have 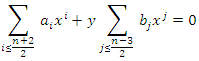 hence
hence 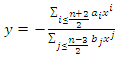 and the relation
and the relation 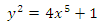 gives the equation
gives the equation 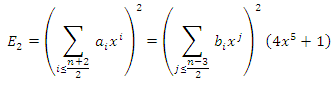 We find a family of points
We find a family of points 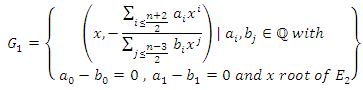 For
For 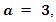 we have
we have 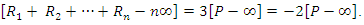 By a similar argument as in case
By a similar argument as in case 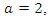 we have
we have 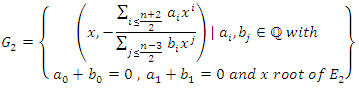 Finally, we have the family
Finally, we have the family 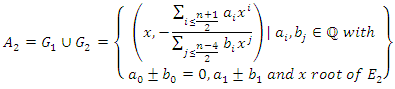
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML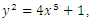 SCIREA Journal of Mathematics, Volume 6, Issue 6, 2021.
SCIREA Journal of Mathematics, Volume 6, Issue 6, 2021.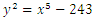 , Asian Research Journal of Mathematics, 51-58, 2021.
, Asian Research Journal of Mathematics, 51-58, 2021.