| [1] | Adams, Y.J and Abdulkadir, S.S. (2018). “On the Extension of the Mover-Stayer Model when rate of transition follows the Negative Binomial Distribution.” American Journal of Mathematics and Statistics, Vol. 8, No. 4, pp. 99 – 104. |
| [2] | Adams, Y.J., Abdulkadir, S.S. and Jibasen, D. (2019). “Mover-Stayer Analysis of Students’ Academic Progress in Modibbo Adama University of Technology, Yola.” Research Journal of Education, Vol. 5, Issue 9, pp: 161 – 166. |
| [3] | Alawadhi, S. and Konsowa, M. (2010). “Marcov Chain Analysis of Student Academicn Progress: An Empirical Comparative Study.” Journal of Modern Applied Statistical Methods, Vol. 9, No. 2, pp. 584 – 595. |
| [4] | Blumen, I. , Kogan, M. , and McCarthy, P.J. (1955). The Industrial Mobility of Labour as a Probability Process. In Spilerman, Seymour (1972). “Extensions of the Mover-Stayer Model.” American Journal of Sociology (AJS), Vol. 78, No. 3, pp. 599-626. |
| [5] | Chukova, S. and Minkova, L.D. (2012). “Characterization of the Polya-Aeppli process.” [Electronic version]. Retrieved from, Sms.victoria.ac.nz/foswiki/pub/Main/ResearchReportSeries/MSOR12 – 02. |
| [6] | Cook, R.J., Kalbfleisch, J.D and Yi, G.Y (2002). “A generalized mover-stayer model for panel data.” Biostatistics, Vol. 3, No. 3, pp. 407-420. Retrieved June 11, 2015 from http://biostatistics.oxfordjournals.org. |
| [7] | Frydman, H (1984). “Maximum Likelihood Estimation in the Mover-Stayer Model.” Journal of American Statistical Association, vol.79, No. 387, p. 632 – 638. |
| [8] | Goodman, L.A. (1961). “Statistical Methods for the Mover-Stayer model.” Journal of American Statistical Association, 56, 841 – 868. |
| [9] | Goodman, L.A. (2013). “Generalizations of the Simple Mover-Stayer Model, Association Models and Quasi-symmetric Models, in the Analysis of Brand-switching Data and other cross-classified Data.” Journal of Empirical Generalizations in Marketing Science, Vol. 14, No. 1, retrieved on October 30, 2016 from; https://www.empgens.com/wp-content/uploads/2013/06/goodman.pdf. |
| [10] | Hoel, P.G., Port, S.C., and Stone, C.J. (1972). Introduction to Stochastic Processes. Boston: Houghton Mifflin Company. |
| [11] | Hodge, R.W. (1966). “Occupational Mobility as a Probability Process” Demography, 3: 19 – 34 in Spilerman, S. (1972). |
| [12] | Johnson, N.L., Kotz, S. and Kemp, A.W. (1992). Univariate Discrete Distributions, 2nd ed., Wiley Series in Probability and Mathematical Statistics: Applied Probability and Statistics, John Wiley & Sons, New York. |
| [13] | Minkova, L.D. (2002). “A Generalization of the Classical Discrete Distributions” Communications in Statistics – Theory and Methods, Vol. 31(6), pp. 871 – 888. |
| [14] | Minkova, L.D. (2004). “The Polya-Aeppli Process and Ruin Problems” Journal of Applied Mathematics and Stochastic Analysis, Vol. 3, pp. 221 – 234. |
| [15] | Minkova, L.D. (2012). “Distributions in Insurance Risk Models” Unpublished doctoral dissertation, Sofia University “St.Kl. Ohridski” Bulgaria. |
| [16] | Minkova, L.D. and Balakrishnan, N. (2014). “On a Bivariate Polya-Aeppli Distribution.” Communications in Statistics – Theory and Methods, Vol. 43, pp. 5026 – 5038. doi: 10.1080/03610926.2012.709906. |
| [17] | Morgan, T.M., Aneshensel, C.S. and Clark, V.A. (1983). “Parameter Estimation for Mover-Stayer models: analyzing depression over time.” Sociological Methods and Research. 11: 345 – 366. |
| [18] | O’ Keefe, A. G., Tom, B.D.M and Farewell, V.T. (2012). “Mixture distributions in multi-state modelling: some considerations in a study of psoriatic arthritis, Statist. Med., 32, 600 – 619. Willey Online Library in Yiu, S., Farewell, V.T. and Tom, B.D.M. (2016). |
| [19] | Spilerman, S. (1970). “Extensions of the Mover-Stayer Model.” Institute for Research on Poverty. Discussion Papers, University of Wisconsin http://www.irp.wisc.edu/publications/dps/pdfs/dt7970.pdf. |
| [20] | Spilerman, S. (1972). “Extensions of the Mover-Stayer Model.” American Journal of Sociology (AJS), Vol. 78, No. 3, pp. 599-626. http://www.jstor.org/stable/2776309. |
| [21] | Yiu, S., Farewell, V.T. and Tom, B.D.M. (2016). “Exploring the Existence od a Stayer Population with Mover-Stayer Counting Process Models: application to joint damage in psoriatic arthritis.” Journal of the Royal Statistical Society: Series C (Applied Statistics). [Electronic version], printed on January 10, 2017. http://onlinelibrary.wiley.com/doi/10.1111/rccs.12187. |


 to model rate of transition in Poisson distribution, which gave the Polya-Aeppli distribution as a mixture. However, that paper did not specify a method or derive an expression for estimating the transition matrix M. This paper attempts to provide a method of estimating the transition matrix M, to compliment the work earlier done by Adams and Abdulkadir (2018). In addition, an attempt was made to obtain an estimate of the stayer population. The obtained expressions were tested using simulated data adopted from Spilerman (1972).
to model rate of transition in Poisson distribution, which gave the Polya-Aeppli distribution as a mixture. However, that paper did not specify a method or derive an expression for estimating the transition matrix M. This paper attempts to provide a method of estimating the transition matrix M, to compliment the work earlier done by Adams and Abdulkadir (2018). In addition, an attempt was made to obtain an estimate of the stayer population. The obtained expressions were tested using simulated data adopted from Spilerman (1972).
 . The choice of the negative binomial as a mixing distribution was informed by considering the number of transitions required to achieved desire events
. The choice of the negative binomial as a mixing distribution was informed by considering the number of transitions required to achieved desire events 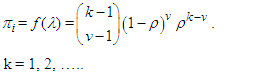
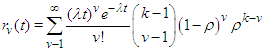
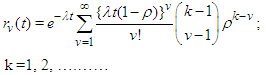
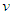 > k. If the parameter
> k. If the parameter 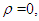 the distribution in (3) reduces to the classical homogenous Poisson distribution (Minkova, 2002; Minkova, 2004; Chukova and Minkova, 2012).Consider individuals with common rate of movement equal to λ at time
the distribution in (3) reduces to the classical homogenous Poisson distribution (Minkova, 2002; Minkova, 2004; Chukova and Minkova, 2012).Consider individuals with common rate of movement equal to λ at time 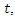 the one-step probability matrix would be given by
the one-step probability matrix would be given by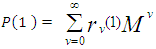
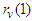 is Poisson distribution with
is Poisson distribution with 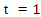 . The transition matrix is obtained by simplifying for M in (4) above.
. The transition matrix is obtained by simplifying for M in (4) above.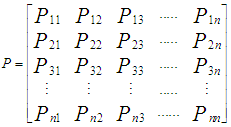
 moves in (0,t) will satisfy a Polya-Aeppli distribution. To obtain an expression for M, the transition matrix for the mover individuals, we used equation (3) in (4)
moves in (0,t) will satisfy a Polya-Aeppli distribution. To obtain an expression for M, the transition matrix for the mover individuals, we used equation (3) in (4)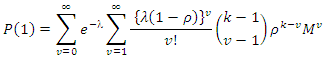
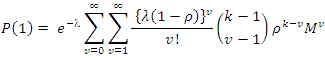
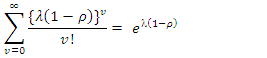
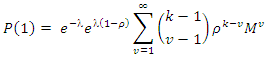
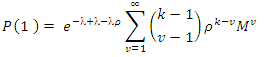
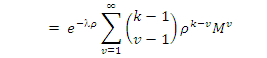
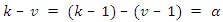
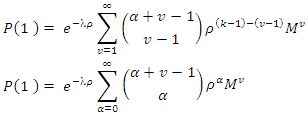
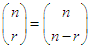
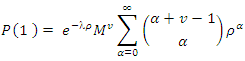
 ; the following binomial expansion holds
; the following binomial expansion holds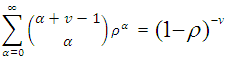
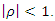
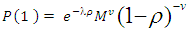
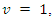 equation (16) becomes
equation (16) becomes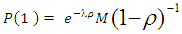
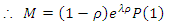
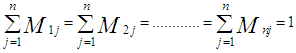
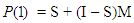
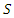 has
has 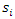 (the proportion initially in the
(the proportion initially in the 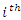 state who are stayers) down the diagonal, and I is the identity matrix. Consequently,
state who are stayers) down the diagonal, and I is the identity matrix. Consequently,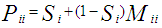
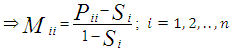
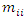 presented above, we obtain the following estimator of
presented above, we obtain the following estimator of 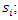
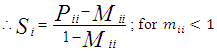
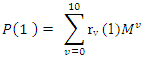

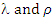 of the Polya Aeppli distribution can be estimated directly from observed data (moment estimates) on the number of moves by an individual. If
of the Polya Aeppli distribution can be estimated directly from observed data (moment estimates) on the number of moves by an individual. If 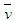 and
and 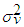 are the sampling mean and variance of this variable (number of moves), then estimates of
are the sampling mean and variance of this variable (number of moves), then estimates of 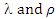 can be obtained in terms of these values (see also Minkova 2012, p. 49). This yield
can be obtained in terms of these values (see also Minkova 2012, p. 49). This yield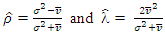
 and
and 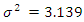 Spilerman (1972), equally estimated
Spilerman (1972), equally estimated 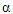 and
and 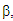 the parameters of the negative binomial distribution using;
the parameters of the negative binomial distribution using; 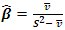 and
and 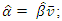 computed from the observed data.Therefore, the estimated λ = 0.9722 and ρ = 0.3527, together with the observed P(1) matrix from equation (23), allow the M* matrix to be derived using equation (18),
computed from the observed data.Therefore, the estimated λ = 0.9722 and ρ = 0.3527, together with the observed P(1) matrix from equation (23), allow the M* matrix to be derived using equation (18), 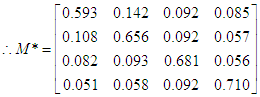
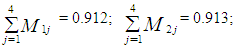
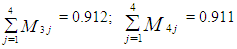
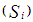
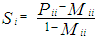
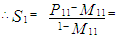
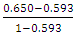 = 0.140Similarly,
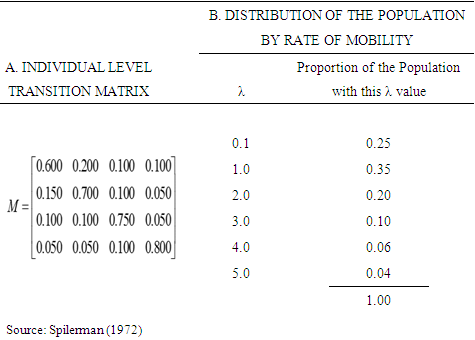
= 0.140Similarly,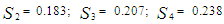 Consequently, the proportions per distribution of number of moves from simulated data, computed from individual-level transition matrix as proposed by Goodman (1961) and Morgan et al (1983) follows;
Consequently, the proportions per distribution of number of moves from simulated data, computed from individual-level transition matrix as proposed by Goodman (1961) and Morgan et al (1983) follows; 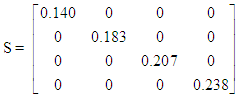
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML