-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2021; 11(3): 67-71
doi:10.5923/j.ajms.20211103.03
Received: Jun. 4, 2021; Accepted: Jun. 25, 2021; Published: Jul. 15, 2021

The Quadratic Equation Concept
Ashwannie Harripersaud
Canje Secondary School, Ministry of Education, Guyana
Correspondence to: Ashwannie Harripersaud, Canje Secondary School, Ministry of Education, Guyana.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The purpose of this essay is to act as a supplement for students who wish to reinforce their knowledge of the quadratic formula. It is not intended to be used as a primary source of education. If so, it should be used in collaboration with an expert of mathematics. This essay focuses primarily on the ways a quadratic equation can be solved. This includes an explanation of factoring, completing the square, the quadratic formula, and references to graphical approaches and analysis.
Keywords: Quadratic, Quadratic equation, Exponent, Coefficient, Discriminant
Cite this paper: Ashwannie Harripersaud, The Quadratic Equation Concept, American Journal of Mathematics and Statistics, Vol. 11 No. 3, 2021, pp. 67-71. doi: 10.5923/j.ajms.20211103.03.
Article Outline
1. Introduction
- The quadratic equation is a formula that is used to solve equations in the form of quadratics. A quadratic is an equation in which the degree, of highest exponent, is a square. The degree also describes the number of possible solutions to the equation (therefore, the number of possible solutions for a quadratic is two). The quadratic formula is as follows:
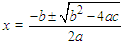 There are other methods used for solving quadratics, such as graphing, factoring, and completing the square. Depending on the quadratic in questions, there is an appropriate time for each method. However, the quadratic formula is advantageous in the fact that it is applicable to all quadratics and will always yield the correct solution.
There are other methods used for solving quadratics, such as graphing, factoring, and completing the square. Depending on the quadratic in questions, there is an appropriate time for each method. However, the quadratic formula is advantageous in the fact that it is applicable to all quadratics and will always yield the correct solution. 2. Literature Review
- The resounding theme in mathematics education research is that students’ performance in the domain of quadratic equations is exceptionally poor and does not significantly increase even after instruction (Chaysuwan, 1996; Vaiyavutjamai et al., 2005). Students have been found to struggle particularly solving for 𝑥 in the form 𝑥 2 = 𝑘 (k>0) and (𝑥 − 𝑟)(𝑥 − 𝑠) = 0 where 𝑟 and 𝑠 are any real numbers (Vaiyavutjamai et al., 2005). It is important to consider the impact and current evidence relating to teaching methods and the learning of quadratic equations. Kotsopoulos (2007) reports that students need to develop procedural and conceptual knowledge through various learning experiences in an integrated manner. The Australian Academy of Science (AAS) also recognizes the intertwined relationship between conceptual understanding, procedural fluency, and problem solving and reasoning due to the hierarchical nature of mathematics (AAS, 2015, p. 17). The cognitive load work by Kirschner, Sweller, and Clark (2006) gives an explanation for the necessity of fluency with prerequisite knowledge. Hattie (2009) notes “fluency with prerequisite knowledge, even at a very early stage, is highly predictive of latter success”. A key process in working with quadratics is solving or finding the 𝑥 intercepts, should there be any. In most curricula this involves factorization, the square root method, completing the square, and the use of the quadratic formula. Each of these techniques has its own advantages and disadvantages when it comes to teaching, learning, and applying. Research has shown that students and teachers shy away from some techniques and favor factorization, generally using coefficients that are easy to factorize since students’ ability to perform fractional and radical arithmetic has been reported as low (Bosse & Nandakumar, 2005). Over-emphasis on relatively simple factorization is concerning since many quadratic equations cannot be factorized. Further, other methods that are more efficient or that develop conceptualization may be neglected in teaching (Bosse & Nandakumar, 2005). For example, factorization with algebra tiles link quadratics with basic multiplication and division concepts via the area model of rectangles and squares (Howden 2001). Geometric models are useful tools that may ensure students are able to understand, manipulate, and apply the quadratic formula via completing the square procedure (Norton, 2015). Barnes (1991) suggests using graphing calculators to plot quadratics with no roots, one root, or two roots and linking this to the discriminate values. Research suggests that teachers tend to avoid teaching alternative methods due to high instances of process skill errors with techniques such as the quadratic formula and completing the square (Zakaria et al., 2010). From this literature review, it is clear that there is a need for further research into the sources of students’ difficulties with quadratic equations.
3. The Quadratic Equation Concept
- The quadratic equation concept can be introduced geometrically by referring to the squares shown in Figures 1 and 2.
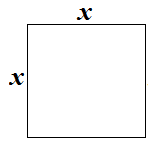 | Figure 1 |
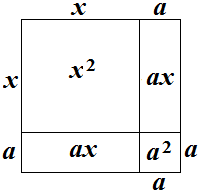 | Figure 2 |
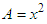 .In Figure 2, geometrically, the area of the larger square is the sum of the individual areas:
.In Figure 2, geometrically, the area of the larger square is the sum of the individual areas: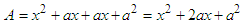 . Algebraically, Figure 2,
. Algebraically, Figure 2, 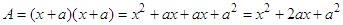 (same result!). This is called a perfect square. Notice that the constant term is the product
(same result!). This is called a perfect square. Notice that the constant term is the product 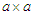 and the coefficient of x is the sum
and the coefficient of x is the sum 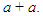 If the sides are not equal, then it is a rectangle, say, of sides
If the sides are not equal, then it is a rectangle, say, of sides 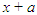 and
and 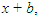 where
where 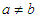 . The area of the rectangle:
. The area of the rectangle: 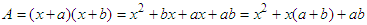 . Notice that the constant term is made up of the product ab and the coefficient of x is the sum
. Notice that the constant term is made up of the product ab and the coefficient of x is the sum 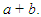 These two ideas are used to factorize quadratic expressions that are factorizable and where the coefficient of x2 is 1, by looking for factors of the constant term, ab, that, when added, give the coefficient of x, i.e.,
These two ideas are used to factorize quadratic expressions that are factorizable and where the coefficient of x2 is 1, by looking for factors of the constant term, ab, that, when added, give the coefficient of x, i.e., 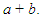 We can extend this idea further to the product of two binomial expressions where the coefficient of x2 is not 1, such as:
We can extend this idea further to the product of two binomial expressions where the coefficient of x2 is not 1, such as: 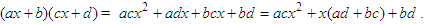 When the coefficient of x2 is multiplied by the constant term the result is acbd, and when two certain factors of this result are added, we get the coefficient of x, i.e., ad + bc. These ideas are used to factorize quadratic expressions which are factorizable and whose x2 coefficient is not 1. The general form of the quadratic equation is:
When the coefficient of x2 is multiplied by the constant term the result is acbd, and when two certain factors of this result are added, we get the coefficient of x, i.e., ad + bc. These ideas are used to factorize quadratic expressions which are factorizable and whose x2 coefficient is not 1. The general form of the quadratic equation is: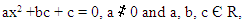 where, a = the coefficient of x2,b = the coefficient of x,c = the constant termand x = the independent variable.The three algebraic methods of solving quadratic equations are:(i) Factorization(ii) Completing the square(iii) Using the quadratic formula.
where, a = the coefficient of x2,b = the coefficient of x,c = the constant termand x = the independent variable.The three algebraic methods of solving quadratic equations are:(i) Factorization(ii) Completing the square(iii) Using the quadratic formula.4. Solution of a Quadratic Equation by Factorization
- If the product mn = 0 and m, n Є R.
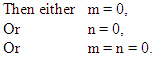 If the product of two factors is equal to zero, then one or both of the factors is equal to zero. Anytime we factorize a quadratic expression, we get the product of two binomial expressions mn. In the case of a quadratic equation, this product is always written equal to zero. These facts allow us to solve quadratic equations using the method of factorization, since either or both of the factors must be equal to zero.Example: Solve the quadratic equation: x2 – 2x = 0Solution:
If the product of two factors is equal to zero, then one or both of the factors is equal to zero. Anytime we factorize a quadratic expression, we get the product of two binomial expressions mn. In the case of a quadratic equation, this product is always written equal to zero. These facts allow us to solve quadratic equations using the method of factorization, since either or both of the factors must be equal to zero.Example: Solve the quadratic equation: x2 – 2x = 0Solution: Hence the solutions are x = 0 or x = 2And the solution set of the quadratic equation is {0, 2}. Question 1: (i) Factorize
Hence the solutions are x = 0 or x = 2And the solution set of the quadratic equation is {0, 2}. Question 1: (i) Factorize 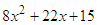 (ii) Solve
(ii) Solve 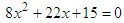 (iii) Graph
(iii) Graph 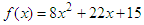 .
.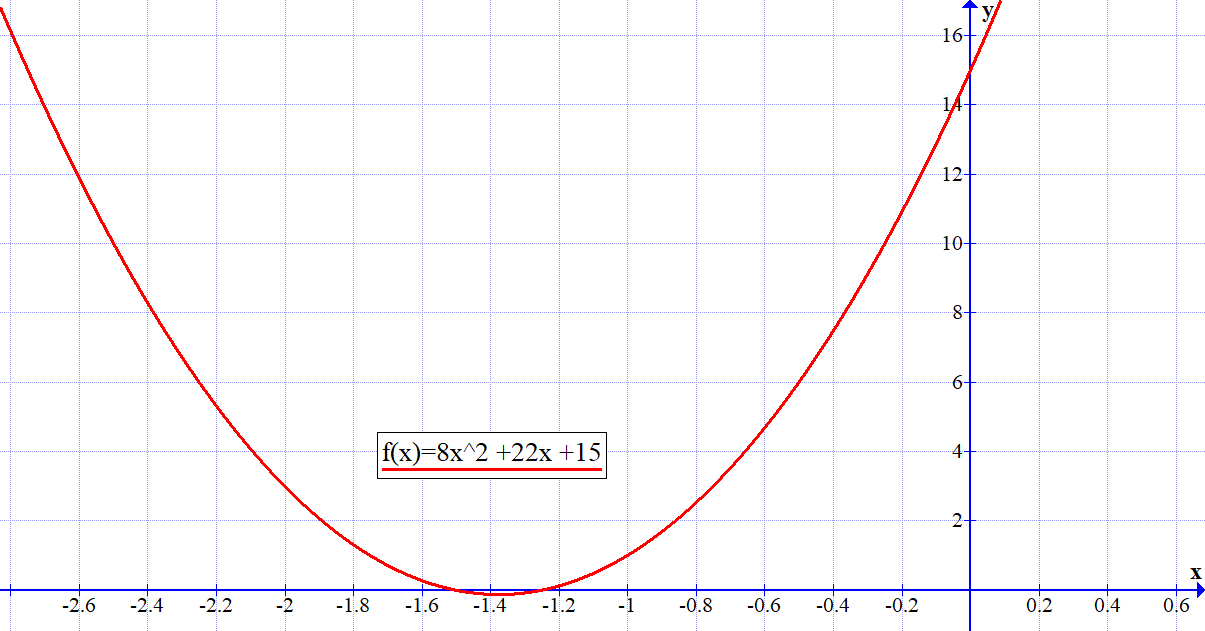 | Figure 3 |
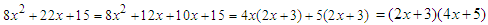 , giving two linear factors.Solving
, giving two linear factors.Solving 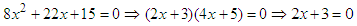 or
or 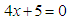 . So,
. So, 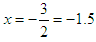 or
or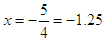 . These are called the solutions or roots of the quadratic equation. The graph of
. These are called the solutions or roots of the quadratic equation. The graph of 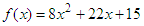 cuts the x-axis at (–1.5, 0) and (–1.25, 0), and cuts the y-axis at (0, 15).It is a minimum graph and the minimum points are at (–1.375, –0.125). Note: Quadratics can only be solved by factorization when they have rational roots. If the roots are irrational or complex, then they cannot be so solved, instead completing the square or the formula method is used.
cuts the x-axis at (–1.5, 0) and (–1.25, 0), and cuts the y-axis at (0, 15).It is a minimum graph and the minimum points are at (–1.375, –0.125). Note: Quadratics can only be solved by factorization when they have rational roots. If the roots are irrational or complex, then they cannot be so solved, instead completing the square or the formula method is used. 5. Solution of a Quadratic Equation by Completing the Square
- Given the quadratic equationax2 + bx + c = 0then grouping the variables, we get(ax2 + bx) + c = 0Factorizing out a, we get
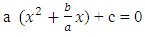 Adding the square of half the coefficient of the term in x to the brackets to make it a perfect square, we get
Adding the square of half the coefficient of the term in x to the brackets to make it a perfect square, we get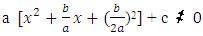 We have changed the left-hand side of the equation by
We have changed the left-hand side of the equation by 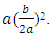 We, therefore, have to subtract this quantity from outside the brackets in order for the original equation to remain unchanged,Since
We, therefore, have to subtract this quantity from outside the brackets in order for the original equation to remain unchanged,Since 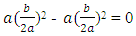 Thus a
Thus a 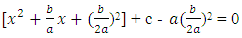 Writing the terms in brackets as a perfect square, we get
Writing the terms in brackets as a perfect square, we get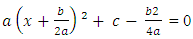 i.e.
i.e. 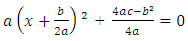 we have finally completed the square.In completing the square, we wrote the quadratic equation in the form:ax² + bx + c = a(x + h)² + kwhere
we have finally completed the square.In completing the square, we wrote the quadratic equation in the form:ax² + bx + c = a(x + h)² + kwhere 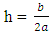 and
and 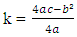 Consider the following series of perfect squares. What relationship do you notice between the coefficient of x and the constant term?
Consider the following series of perfect squares. What relationship do you notice between the coefficient of x and the constant term? 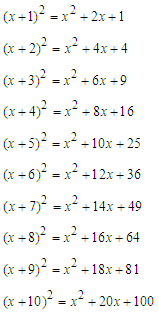 The square of half the coefficient of x is equal to the constant term, i.e., (½ coefficient of x) 2 = constant term.Alternatively, half the coefficient of x is equal to the square root of the constant term, i.e., ½ coefficient of x = √ (constant term).The first statement expressing the relationship is more useful for completing the square for quadratic expressions that are not perfect squares. This is why this method is called ‘completing the square’ as it literally converts a rectangle into a perfect square by adding some ‘bits and pieces’ to the rectangle (discussed above) until the perfect square is completed. The technique of adding the ‘bits and pieces’ is shown below. Solve the equation
The square of half the coefficient of x is equal to the constant term, i.e., (½ coefficient of x) 2 = constant term.Alternatively, half the coefficient of x is equal to the square root of the constant term, i.e., ½ coefficient of x = √ (constant term).The first statement expressing the relationship is more useful for completing the square for quadratic expressions that are not perfect squares. This is why this method is called ‘completing the square’ as it literally converts a rectangle into a perfect square by adding some ‘bits and pieces’ to the rectangle (discussed above) until the perfect square is completed. The technique of adding the ‘bits and pieces’ is shown below. Solve the equation 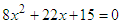 by completing the square.Divide throughout by 8 (possible since the equation = 0):
by completing the square.Divide throughout by 8 (possible since the equation = 0): 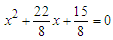 Subtracting
Subtracting 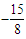 from both sides:
from both sides: 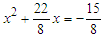 Completing the square for LHS and keeping it equal to RHS:
Completing the square for LHS and keeping it equal to RHS: 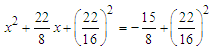 Since LHS is now a perfect square:
Since LHS is now a perfect square: 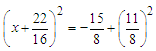 Simplifying both sides:
Simplifying both sides: 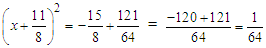 Square root both sides:
Square root both sides: 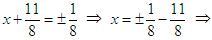 Two solutions or roots:
Two solutions or roots: 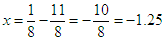 or
or 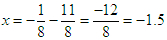 (same roots as obtained earlier).
(same roots as obtained earlier). 6. Solution of a Quadratic Equation Using the Quadratic Formula
- The quadratic formula is obtained by completing the square for the general quadratic equation.Given the quadratic equationax² + bx + c = 0Taking the constant term to the right-hand side, we getax² + bx = -cDividing both sides by a, we get
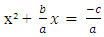 Adding the square of half the coefficient of x to both sides of the equation, we get
Adding the square of half the coefficient of x to both sides of the equation, we get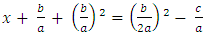 The left-hand side is now a perfect square.Thus,
The left-hand side is now a perfect square.Thus, 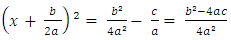 Taking square roots, we get
Taking square roots, we get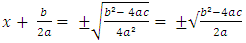 i.e.
i.e. 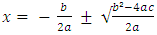
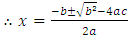 This equation is called the quadratic formula and can be used to solve any quadratic equation.The idea is to make x the subject of the formula by completing the square (as shown above) and using algebraic manipulation until you obtain the formula:
This equation is called the quadratic formula and can be used to solve any quadratic equation.The idea is to make x the subject of the formula by completing the square (as shown above) and using algebraic manipulation until you obtain the formula: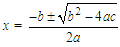 Note: The vinculum (fraction bar) extends all the way under the numerator and not only under the radical sign (square root) only!The general quadratic expression ax2+ bx + c can be set equal to y, thus: ax2+ bx + c= y and then we proceed to make x the subject by completing the square as shown below.
Note: The vinculum (fraction bar) extends all the way under the numerator and not only under the radical sign (square root) only!The general quadratic expression ax2+ bx + c can be set equal to y, thus: ax2+ bx + c= y and then we proceed to make x the subject by completing the square as shown below.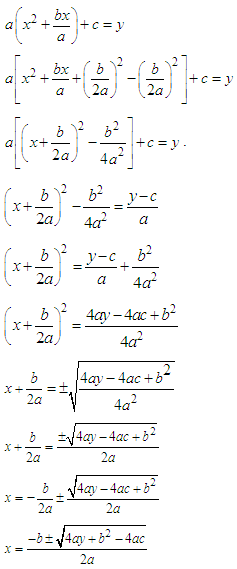 Given: ax2+ bx + c = 0, make x the subject. Let y = 0 in the above formula for x:
Given: ax2+ bx + c = 0, make x the subject. Let y = 0 in the above formula for x: 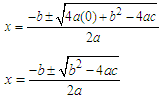 The term b2 – 4ac is called the discriminant, D, and can have values = 0, > 0 or < 0. The discriminant can be used to determine the nature of the roots of a quadratic equation, that is, whether the equation has identical real roots or different real roots or complex roots. Additionally, when D = square number, the equation has two rational roots, and when D = non-square number, the equation has two irrational roots.
The term b2 – 4ac is called the discriminant, D, and can have values = 0, > 0 or < 0. The discriminant can be used to determine the nature of the roots of a quadratic equation, that is, whether the equation has identical real roots or different real roots or complex roots. Additionally, when D = square number, the equation has two rational roots, and when D = non-square number, the equation has two irrational roots.7. Conclusions
- The quadratic formula is a useful alternative to obtaining information about quadratics. It has disadvantages and advantages in relation to such methods of completing the square, factoring, and graphing. Thus, it should be used appropriately. The quadratic formula can be applied in numerous ways. It can be applied to the changes essential to calculus, the study of objects in motion (more generally, it is the study of motion). The quadratic equation and its application must be fully understood in order to appreciate both the beauty and complexity of mathematics.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML