-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2021; 11(3): 59-60
doi:10.5923/j.ajms.20211103.01
Received: Apr. 6, 2021; Accepted: Apr. 16, 2021; Published: May 15, 2021

Cancellation Series
Ameha Tefera Tessema
Strategic Planning, Commercial Bank of Ethiopia, Addis Ababa, Ethiopia
Correspondence to: Ameha Tefera Tessema, Strategic Planning, Commercial Bank of Ethiopia, Addis Ababa, Ethiopia.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Mathematical series play an important role in various aspects of our life and help to predict, evaluate and monitor the outcome of a situation in order to pass decision. The purpose of this paper is to develop a new kind of series and the sum or deduction of two terms of which fractionally cancel in order to get the cancellation result 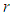 . let for all
. let for all 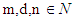 and let
and let 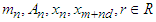 such that
such that 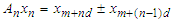 and
and 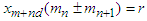 then
then 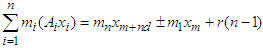 .
.
Keywords: Series, Cancellation series
Cite this paper: Ameha Tefera Tessema, Cancellation Series, American Journal of Mathematics and Statistics, Vol. 11 No. 3, 2021, pp. 59-60. doi: 10.5923/j.ajms.20211103.01.
1. Introduction
- Telescoping series is a very important series for nowadays technology achievement. It is very simple to use because of its alternative, positive and negative, sign for the same term in order to get cancellation zero [7]. In telescoping, the sum of series
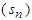 must be represented only by
must be represented only by 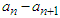 after each term cancelling with part of the next term is known as the method of differences [6] [2]. A telescoping product is a finite product (or the partial product of an infinite product) that can be cancelled by method of quotients to be eventually only a finite number of factors [5] [1]. Unless each term of a sequence related with one to another through succession of the same pattern, there is no formula if the sequence terms are succession of random number [3]. The idea of telescoping a series is widely known, but is not widely trusted. It is often treated as a formalism with no meaning, unless convergence is already established. even for divergent series, the results of telescoping are self-consistent, and consistent with other well-behaved summation operations. Moreover, the summation operations obtained by telescoping are the strongest possible operations with these properties [4]. However, on this paper I want to show that how a new series can be formed rather than telescoping series. The purpose of the method is to get the cancellation
after each term cancelling with part of the next term is known as the method of differences [6] [2]. A telescoping product is a finite product (or the partial product of an infinite product) that can be cancelled by method of quotients to be eventually only a finite number of factors [5] [1]. Unless each term of a sequence related with one to another through succession of the same pattern, there is no formula if the sequence terms are succession of random number [3]. The idea of telescoping a series is widely known, but is not widely trusted. It is often treated as a formalism with no meaning, unless convergence is already established. even for divergent series, the results of telescoping are self-consistent, and consistent with other well-behaved summation operations. Moreover, the summation operations obtained by telescoping are the strongest possible operations with these properties [4]. However, on this paper I want to show that how a new series can be formed rather than telescoping series. The purpose of the method is to get the cancellation 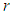 and to form a new kind of series. The process of cancellation of telescoping series is straight, but the process of cancellation of this paper is fractional. Therefore, this paper does have an effort in solving different mathematical problems.Theorem 1: let for all
and to form a new kind of series. The process of cancellation of telescoping series is straight, but the process of cancellation of this paper is fractional. Therefore, this paper does have an effort in solving different mathematical problems.Theorem 1: let for all 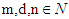 (Natural numbers) and let
(Natural numbers) and let 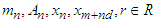 (Real Numbers) such that
(Real Numbers) such that 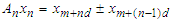 and
and 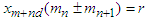 then
then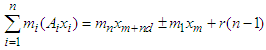 Proof. let for all
Proof. let for all 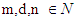 and let
and let 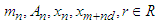 such that
such that 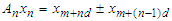 and
and 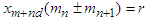 then
then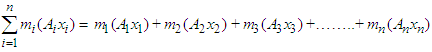
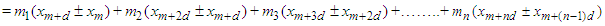 Gathering the same terms, we have the following
Gathering the same terms, we have the following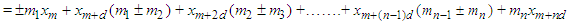 Therefore, we have
Therefore, we have 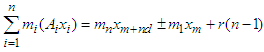
2. Conclusions
- The cancellation series can generate different kinds of unknown but viable series, which can be a base for number theory specifically and for mathematics in general. The benefit of this series enables us to add up sequences of couple terms having similar pattern. Here the end result of cancellation series is the difference or addition between the first and last terms and the number of cancelled results even though the result of telescoping series leaves the difference between first and last term. It also utilizes the technique of Partial Fractions which is a way for us to express a rational function (algebraic fraction) as a sum of simpler fractions. The method does have a great addition to mathematics by simplifying tedious series into three terms.Illustration:Let the series be 3+3+5/2+3+27/8, this can be simplified as follows3+3+5/2+3+27/8 =
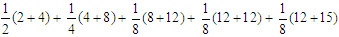 3+3+5/2+3+27/8 =
3+3+5/2+3+27/8 =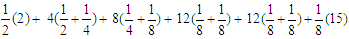 3+3+5/2+3+27/8 =1+3+3+3+3+15/83+3+5/2+3+27/8 =1+4x3+15/8
3+3+5/2+3+27/8 =1+3+3+3+3+15/83+3+5/2+3+27/8 =1+4x3+15/8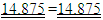
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML