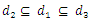-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2021; 11(2): 27-33
doi:10.5923/j.ajms.20211102.01
Received: Jan. 31, 2021; Accepted: Mar. 5, 2021; Published: Mar. 15, 2021

Network Flows with Arc Reversals and Non-Symmetric Transit Times
Shiva Prakash Gupta 1, Urmila Pyakurel 2, Tanka Nath Dhamala 2
1Tribhuvan University, Tri-Chandra Multiple Campus, Kathmandu, Nepal
2Central Department of Mathematics, Tribhuvan University, Kathmandu, Nepal
Correspondence to: Urmila Pyakurel , Central Department of Mathematics, Tribhuvan University, Kathmandu, Nepal.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The contraflow technique has been extensively used to evacuate people in disasters situation. By flipping the orientation of necessary road segments, the flow value increases, and the evacuation time decreases significantly. Contraflow problems with asymmetric capacity and symmetric transit time on arcs have polynomial-time solutions. But in uneven road network topology, transit time may not be symmetrical, even affected by time or flow dependency. Recently, the two-terminal maximum dynamic and earliest arrival partial contraflow problems with non-symmetric capacity and transit time on arcs are solved polynomially. In this paper, we introduce two flow problems with asymmetric transit time. First, we present the multi-source single-sink earliest arrival transshipment contraflow problem, which deals with evacuating the maximum number of people each time. Second, the single-source multi-sink prioritized maximum dynamic partial contraflow problem that evacuates the people by assigning priority to critically injured people. We also provide polynomial-time algorithms to solve these problems.
Keywords: Evacuation network, Network flow, Non-symmetric transit time, Lexicographic flow, Earliest arrival transshipment, Contraflow
Cite this paper: Shiva Prakash Gupta , Urmila Pyakurel , Tanka Nath Dhamala , Network Flows with Arc Reversals and Non-Symmetric Transit Times, American Journal of Mathematics and Statistics, Vol. 11 No. 2, 2021, pp. 27-33. doi: 10.5923/j.ajms.20211102.01.
Article Outline
1. Introduction
- The human population has been in danger due to increasing number of different natural and man-made disasters, like floods, tsunamis, landslides, earthquakes, chemical explosions and terrorist attacks. An efficient evacuation strategy is required to save lives and property in such a situation. The strategy incorporates the four steps preparedness, planning, response, and recovery. Preparedness deals with the reduction or elimination of the effects of a hazard. The planning step draws a layout for the efficient evacuation. The response phase involves actions, whereas the recovery seeks to bring back the situation into normalcy. The evacuation network is considered, as a network associated with the transmission of people or commodities from disaster zones (sources) to the safety zones (sinks). The sources, sinks, and the junction of road segments constitute the nodes. The connections between the two nodes signify the arcs. On each arc, the capacity that limits the flow amount (i.e., transported people or goods), and the travel time are allocated. Historically, the study of flows model on networks mainly originated from problems related to the transportation of materials and people.With the outstanding work of Ford and Fulkerson [9], a systematic mathematical treatment of network flow theory started. Flow over time, that is known as dynamic flow in literature, is different from classical static flows without time component. In [10], they only consider the problem of sending the maximum amount of flow from a source
 to a sink
to a sink 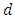 for fixed time horizon T. Gale [11] comes across the question of whether it is possible to send the maximum amount of flow from a source
for fixed time horizon T. Gale [11] comes across the question of whether it is possible to send the maximum amount of flow from a source 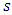 to a sink
to a sink 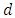 at each time point. He develops a more general theory in which flow is maximized on each time point known as the earliest arrival flows, but unable to provide an algorithm to solve this problem. Wilkinson [28] and Minieka [15] designed the algorithms to solve this problem in two-terminal network. For the general problem in multi-source and multi-sink network, the earliest arrival flow does not exist. But it does always exist for multi-source single-sink network with given supplies and demands [3]. In evacuation scenarios, sometimes it is necessary to provide priority on the certain terminals. If we maximize the flow from the source(s) to the sink(s) with given priority on terminals, then it is known as lexicographic maximum flow. The lexicographic maximum static flow problem with the multi-source multi-sink network is solved in polynomial-time [15]. The dynamic version of this problem with given priority ordering on terminals is presented by Hoppe and Tardos [14,13]. They also provide a polynomial-time solution for this problem, which plays an important role in some cases of evacuation planning.Contraflow or lane reversals is a technique that increases the capacity of the lanes by flipping the orientation of opposite road segments of the transportation network topology in a fixed direction that increase the flow value and decrease the time. It has been primarily used as a part of evacuation schemes that increase the efficiency of traffic movement during an evacuation process by reverting incoming lanes towards the disastrous area. Kim et al. [15] presented greedy and bottleneck relief heuristics to solve the contraflow problem and experimental result shows that evacuation time can be reduced by at least 40% by reversing at most 30% of the arcs. Rebennack et al. [27] introduce the models and provide analytical solutions for the two-terminal maximum and quickest flow problems with asymmetric capacity and symmetric transit time on arcs. They develop strongly polynomial-time algorithms, where lane reversals are made at time zero and kept fixed afterward.With the help of natural transformation, authors in [20,22] extended the discrete-time dynamic contraflow solutions to continuous-time settings. Pyakurel et al. [23] solved these continuous-time problems in the abstract network. The complexity of quickest contraflow problem was improved by solving the min-cost flow problem in [25]. Pyakurel and Dhamala [19] investigated the lexicographic maximum static and dynamic contraflow problems and presented polynomial-time solutions. The quickest facility location problems with or without contraflow were investigated in [17]. Dhungana and Dhamala [8] presented polynomial-time solutions to budget constraint contraflow problems. Authors in [18] solved network flow problem with intermediate storage. Furthermore, an integrated approach in the transit -based evacuation was investigated in [1]. Authors in [26] introduced a partial contraflow technique that increase the flow value also minimize the time, and saves unused arc capacities that can be used in emergency periods. Dhamala et al. [6] introduced same technique in the quickest multi-commodity problems and presented two approximation algorithms in a discrete-time setting. Authors in [24] provided efficient algorithms to solve maximum multi-commodity flow over time problems by using same approach. Gupta et al. [12] extended the result of [6] in a continuous-time setting.In all the contraflow problems discussed above, it is assumed that capacity is asymmetric, but transit time is symmetric on anti-parallel arcs. This assumption is not true in all cases due to the uneven road network in urban areas because of many reasons, for example time and flow dependency of the road segments. Therefore, transit time may not be symmetric in all cases of contraflow configuration. Bhandari and Khadka [4] studied the two-terminal maximum dynamic contraflow problem with non-symmetric transit times on anti-parallel arcs such that the reversals use the same arc transit time as it took before. This interprets the case of parallel arcs on the network using algorithm of [27]. Recently, Nath et al. [16] investigated contraflow problem with asymmetric capacity and transit time on arcs and presented a new solution approach to solve this problem such that a reversed arc takes travel time as that of unreversed counterpart. Therefore, it uses the property of asymmetric arc travel times and modifies the algorithm of [27]. By using the approach of Nath et al. [16], we introduce the multi-source single-sink earliest arrival partial contra-transshipment (EAPCT) problem, and provide polynomial-time solution. With such asymmetric arc travel times, we also present a polynomial-time algorithm to solve the lexicographic maximum partial contraflow (LMPCF) for single-source multi-sink network. This study minimizes the evacuation time and casualties significantly by assigning priority to critically injured people on uneven network topology. In our evacuation model, we assume that arc capacity and transit time are constant. In reality, the transit time of an arc is not constant but flow-dependent. To implement the contraflow approach on a road network, significant quantity of resources are required such as, traffic police and safety facilities. The rest of the paper is organized as follows. In Section 2, we give some basic notations and models used throughout the paper. We introduce the EAPCT problem with non-symmetric transit times on anti-parallel arcs and present an algorithm to solve it in Section 3. The LMPCF problem with non-symmetric transit times is introduced in Section 4. In this section, we present a polynomial-time algorithm to solve this problem. Section 5 concludes the paper.
at each time point. He develops a more general theory in which flow is maximized on each time point known as the earliest arrival flows, but unable to provide an algorithm to solve this problem. Wilkinson [28] and Minieka [15] designed the algorithms to solve this problem in two-terminal network. For the general problem in multi-source and multi-sink network, the earliest arrival flow does not exist. But it does always exist for multi-source single-sink network with given supplies and demands [3]. In evacuation scenarios, sometimes it is necessary to provide priority on the certain terminals. If we maximize the flow from the source(s) to the sink(s) with given priority on terminals, then it is known as lexicographic maximum flow. The lexicographic maximum static flow problem with the multi-source multi-sink network is solved in polynomial-time [15]. The dynamic version of this problem with given priority ordering on terminals is presented by Hoppe and Tardos [14,13]. They also provide a polynomial-time solution for this problem, which plays an important role in some cases of evacuation planning.Contraflow or lane reversals is a technique that increases the capacity of the lanes by flipping the orientation of opposite road segments of the transportation network topology in a fixed direction that increase the flow value and decrease the time. It has been primarily used as a part of evacuation schemes that increase the efficiency of traffic movement during an evacuation process by reverting incoming lanes towards the disastrous area. Kim et al. [15] presented greedy and bottleneck relief heuristics to solve the contraflow problem and experimental result shows that evacuation time can be reduced by at least 40% by reversing at most 30% of the arcs. Rebennack et al. [27] introduce the models and provide analytical solutions for the two-terminal maximum and quickest flow problems with asymmetric capacity and symmetric transit time on arcs. They develop strongly polynomial-time algorithms, where lane reversals are made at time zero and kept fixed afterward.With the help of natural transformation, authors in [20,22] extended the discrete-time dynamic contraflow solutions to continuous-time settings. Pyakurel et al. [23] solved these continuous-time problems in the abstract network. The complexity of quickest contraflow problem was improved by solving the min-cost flow problem in [25]. Pyakurel and Dhamala [19] investigated the lexicographic maximum static and dynamic contraflow problems and presented polynomial-time solutions. The quickest facility location problems with or without contraflow were investigated in [17]. Dhungana and Dhamala [8] presented polynomial-time solutions to budget constraint contraflow problems. Authors in [18] solved network flow problem with intermediate storage. Furthermore, an integrated approach in the transit -based evacuation was investigated in [1]. Authors in [26] introduced a partial contraflow technique that increase the flow value also minimize the time, and saves unused arc capacities that can be used in emergency periods. Dhamala et al. [6] introduced same technique in the quickest multi-commodity problems and presented two approximation algorithms in a discrete-time setting. Authors in [24] provided efficient algorithms to solve maximum multi-commodity flow over time problems by using same approach. Gupta et al. [12] extended the result of [6] in a continuous-time setting.In all the contraflow problems discussed above, it is assumed that capacity is asymmetric, but transit time is symmetric on anti-parallel arcs. This assumption is not true in all cases due to the uneven road network in urban areas because of many reasons, for example time and flow dependency of the road segments. Therefore, transit time may not be symmetric in all cases of contraflow configuration. Bhandari and Khadka [4] studied the two-terminal maximum dynamic contraflow problem with non-symmetric transit times on anti-parallel arcs such that the reversals use the same arc transit time as it took before. This interprets the case of parallel arcs on the network using algorithm of [27]. Recently, Nath et al. [16] investigated contraflow problem with asymmetric capacity and transit time on arcs and presented a new solution approach to solve this problem such that a reversed arc takes travel time as that of unreversed counterpart. Therefore, it uses the property of asymmetric arc travel times and modifies the algorithm of [27]. By using the approach of Nath et al. [16], we introduce the multi-source single-sink earliest arrival partial contra-transshipment (EAPCT) problem, and provide polynomial-time solution. With such asymmetric arc travel times, we also present a polynomial-time algorithm to solve the lexicographic maximum partial contraflow (LMPCF) for single-source multi-sink network. This study minimizes the evacuation time and casualties significantly by assigning priority to critically injured people on uneven network topology. In our evacuation model, we assume that arc capacity and transit time are constant. In reality, the transit time of an arc is not constant but flow-dependent. To implement the contraflow approach on a road network, significant quantity of resources are required such as, traffic police and safety facilities. The rest of the paper is organized as follows. In Section 2, we give some basic notations and models used throughout the paper. We introduce the EAPCT problem with non-symmetric transit times on anti-parallel arcs and present an algorithm to solve it in Section 3. The LMPCF problem with non-symmetric transit times is introduced in Section 4. In this section, we present a polynomial-time algorithm to solve this problem. Section 5 concludes the paper.2. Mathematical Formulations
- The necessary denotations and mathematical formulations are set for the flow models, where reversals of arcs are permitted that improves an objective value by flipping their orientations whenever necessary.
2.1. Flow Models
- Let us consider a dynamic network topology
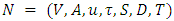 with node set
with node set 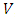 , arc set
, arc set 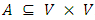 . We take
. We take 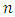 and
and 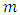 to denote the number of nodes and arcs in
to denote the number of nodes and arcs in 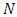 . The capacity function
. The capacity function 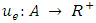 restricts the flow that can enter the arc and a transit time function
restricts the flow that can enter the arc and a transit time function 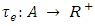 measures the arc traversal time. The time period
measures the arc traversal time. The time period 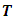 is denoted by
is denoted by 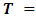
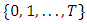 in discrete and
in discrete and 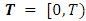 in continuous-time settings. We assume
in continuous-time settings. We assume  and
and 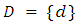 for single-source single-sink flow problem.For a given
for single-source single-sink flow problem.For a given 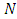 , the corresponding auxiliary network is denoted by
, the corresponding auxiliary network is denoted by 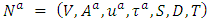 , with undirected edges in
, with undirected edges in 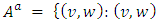 or
or 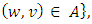 where
where 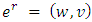 is the reversed arc of
is the reversed arc of 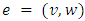 . The capacity of the auxiliary arc is the sum of capacities of arcs e and er such that
. The capacity of the auxiliary arc is the sum of capacities of arcs e and er such that 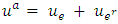 , where
, where 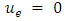 if
if 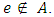 Due to uneven road network, transit time from
Due to uneven road network, transit time from 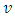 to
to 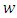 of an arc
of an arc 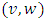 is different from
is different from 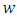 to
to 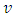 that means it is non-symmetrical as shown in Figure 1(a). The transit time of auxiliary arc
that means it is non-symmetrical as shown in Figure 1(a). The transit time of auxiliary arc 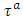 depends on its orientation as shown in Figure 1(b) and 1(c). In the case of a one-way road network between two nodes, we assume that
depends on its orientation as shown in Figure 1(b) and 1(c). In the case of a one-way road network between two nodes, we assume that 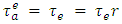 for contraflow configuration. Other network parameters are unaltered.
for contraflow configuration. Other network parameters are unaltered.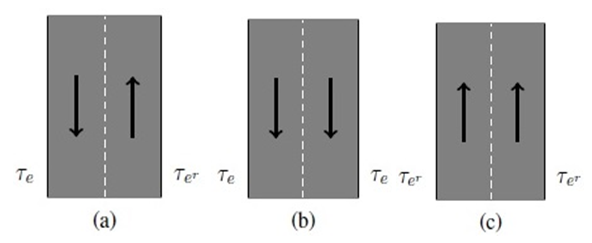 | Figure 1. (a) Represents a two-way road network, (b) represents the network, if arc  is reversed in the direction of arc e, and (c) represents the network, if arc e is reversed in the direction of arc is reversed in the direction of arc e, and (c) represents the network, if arc e is reversed in the direction of arc  |
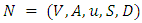 . Many properties developed based on static network topology are the foundation for most of the real-world dynamic flow problems. By considering the auxiliary network
. Many properties developed based on static network topology are the foundation for most of the real-world dynamic flow problems. By considering the auxiliary network 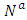 as a two-way directed one, we use it as the network
as a two-way directed one, we use it as the network 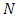 in the following models.Static flow with lane reversals. A static flow
in the following models.Static flow with lane reversals. A static flow 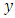 for the given static network
for the given static network 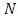 without time dimension is defined by the function
without time dimension is defined by the function 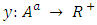 with flow value
with flow value  satisfying
satisfying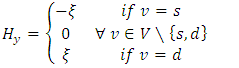 | (1) |
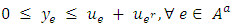 | (2) |
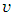 is
is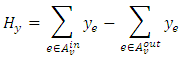 The sets
The sets 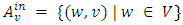 and
and 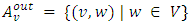 denote incoming arcs to node
denote incoming arcs to node 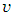 , and outgoing arcs from node
, and outgoing arcs from node 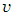 respectively, such that
respectively, such that 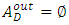 and
and 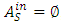 , except in the lane reversal network. The second condition of the constraints in (1) is flow conservation constraints at intermediate nodes. The constraints in (2) are capacity constraints bounded by capacities of the auxiliary network. Rebennack et al. [27] presented a polynomial-time algorithm for a single-source single-sink maximum static contraflow problem which is the backbone for further study. They also provided a polynomial-time solution of multi-source multi-sink static network problem.Dynamic flow with lane reversals. For a given dynamic network
, except in the lane reversal network. The second condition of the constraints in (1) is flow conservation constraints at intermediate nodes. The constraints in (2) are capacity constraints bounded by capacities of the auxiliary network. Rebennack et al. [27] presented a polynomial-time algorithm for a single-source single-sink maximum static contraflow problem which is the backbone for further study. They also provided a polynomial-time solution of multi-source multi-sink static network problem.Dynamic flow with lane reversals. For a given dynamic network 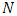 with constant transit time, a flow over time
with constant transit time, a flow over time 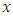 defined by
defined by 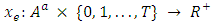 with flow value
with flow value 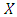 satisfies the constraints (3-5).
satisfies the constraints (3-5).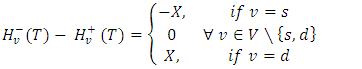 | (3) |
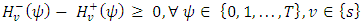 | (4) |
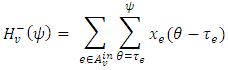 and
and 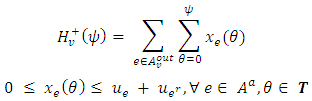 | (5) |
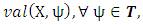 in (6) satisfying the constraints (3-5).
in (6) satisfying the constraints (3-5).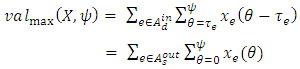 | (6) |
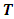 .Here, the second condition of the constraints in (3) are flow conservation constraints at time horizon T, whereas the constraints in (4) represent non-conservation of flow at intermediate time points
.Here, the second condition of the constraints in (3) are flow conservation constraints at time horizon T, whereas the constraints in (4) represent non-conservation of flow at intermediate time points 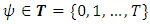 in discrete-time setting. Similarly, the capacity constraints in (5) are bounded above by the capacities with lane reversals.Maximum dynamic partial contraflow with non-symmetric capacity and transit time. Maximum dynamic partial contraflow is the maximization of an
in discrete-time setting. Similarly, the capacity constraints in (5) are bounded above by the capacities with lane reversals.Maximum dynamic partial contraflow with non-symmetric capacity and transit time. Maximum dynamic partial contraflow is the maximization of an 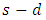 flow in a given time horizon
flow in a given time horizon 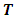 if the direction of arcs can be switched at time zero. This approach saves the unused arc capacities that can be used in case of emergency. The authors in [26] presented a polynomial-time algorithm for the maximum dynamic partial contraflow problem with asymmetric capacities and symmetric transit times. Nath et al. [16] presented an algorithm and proved the correctness for both parameters as asymmetric. Their algorithm modifies the network with arc capacity as the sum of two-ways capacities and the transit time taken as that of non-reversed arcs of the auxiliary network (cf. Figure 1(b), 1(c)). If there is a one-way arc, then
if the direction of arcs can be switched at time zero. This approach saves the unused arc capacities that can be used in case of emergency. The authors in [26] presented a polynomial-time algorithm for the maximum dynamic partial contraflow problem with asymmetric capacities and symmetric transit times. Nath et al. [16] presented an algorithm and proved the correctness for both parameters as asymmetric. Their algorithm modifies the network with arc capacity as the sum of two-ways capacities and the transit time taken as that of non-reversed arcs of the auxiliary network (cf. Figure 1(b), 1(c)). If there is a one-way arc, then 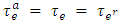 holds. Then a maximum dynamic flow is calculated by using a temporally repeated flow algorithm and flow is decomposed into paths and cycles. A removal of positive flows on cycles ensures that the flow moves in only one direction but not in both. This approach can be extended to the EAPCT and LMPCF problems, that we propose in the next sections.
holds. Then a maximum dynamic flow is calculated by using a temporally repeated flow algorithm and flow is decomposed into paths and cycles. A removal of positive flows on cycles ensures that the flow moves in only one direction but not in both. This approach can be extended to the EAPCT and LMPCF problems, that we propose in the next sections.3. EAPCT Problem with Asymmetric Capacity and Transit Time
- In the evacuation, it is not possible to calculate the exact evacuation time in advance. So, it is better to send a maximum number of evacuees at each time
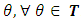 . Authors in [4,16] solved
. Authors in [4,16] solved 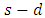 earliest arrival contraflow problem with asymmetric capacity and transit time. But the earliest arrival contraflow problem for multi-source multi-sink network is NP-hard as the MDPCF problem for multi-source multi-sink network is NP-hard. Pyakurel and Dhamala [21] presented an efficient algorithm to solve the multi-source single-sink earliest arrival contraflow problem with given supplies and demands at terminals and having the asymmetric capacity and symmetric transit time. We extend this result for EAPCT problem in this section.Problem 1. Consider a multi-source single-sink network
earliest arrival contraflow problem with asymmetric capacity and transit time. But the earliest arrival contraflow problem for multi-source multi-sink network is NP-hard as the MDPCF problem for multi-source multi-sink network is NP-hard. Pyakurel and Dhamala [21] presented an efficient algorithm to solve the multi-source single-sink earliest arrival contraflow problem with given supplies and demands at terminals and having the asymmetric capacity and symmetric transit time. We extend this result for EAPCT problem in this section.Problem 1. Consider a multi-source single-sink network 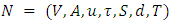 with given supplies and demand at the terminal nodes and having the constant non-symmetric capacity and transit time on each arc
with given supplies and demand at the terminal nodes and having the constant non-symmetric capacity and transit time on each arc 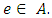 The EAPCT problem is to compute a maximum
The EAPCT problem is to compute a maximum 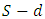 flow at each time satisfying the demands and supplies within time T such that the direction of arcs can be switched without any cost.Algorithm 1: The EAPCT algorithm with asymmetric arc parametersInput: Given a dynamic network
flow at each time satisfying the demands and supplies within time T such that the direction of arcs can be switched without any cost.Algorithm 1: The EAPCT algorithm with asymmetric arc parametersInput: Given a dynamic network 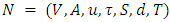 with constant and non-symmetric transit time and source-sink supply-demand vector
with constant and non-symmetric transit time and source-sink supply-demand vector 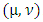 .Output: An EAPCT1. The given network is transformed into the auxiliary network
.Output: An EAPCT1. The given network is transformed into the auxiliary network 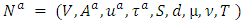 by adding two-way arc capacities such as
by adding two-way arc capacities such as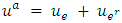
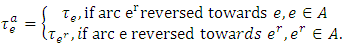 2. Construct the extended network
2. Construct the extended network 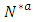 of
of 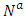 by adding super source and connect other sources to super source by an arc.3. Compute maximum dynamic flow on extended network
by adding super source and connect other sources to super source by an arc.3. Compute maximum dynamic flow on extended network 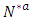 by using algorithm of Pyakurel and Dhamala [21].4. Decompose the flow
by using algorithm of Pyakurel and Dhamala [21].4. Decompose the flow 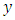 along paths and cycles and remove the flow in cycles.5. Reverse
along paths and cycles and remove the flow in cycles.5. Reverse 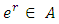 up to the capacity
up to the capacity 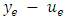 iff
iff 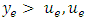 replaced by 0 whenever
replaced by 0 whenever 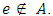 6. For each
6. For each 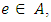 if
if 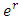 is reversed,
is reversed, 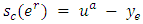 and
and 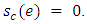 If neither
If neither 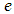 nor
nor 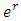 is reversed,
is reversed, 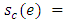
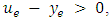 where
where 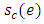 is the saved capacity of e.7. Transform the solution to the original network.Theorem 1. Algorithm 1 solves the EAPCT with asymmetric capacity and transit time on network
is the saved capacity of e.7. Transform the solution to the original network.Theorem 1. Algorithm 1 solves the EAPCT with asymmetric capacity and transit time on network 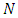 optimally.Proof. The proof of the theorem consists of two steps. First, we show the feasibility. For this, we only have to show that Step 5 of the algorithm is feasible. Step 3 is feasible as shown in [21]. After applying Step 4 the flow is either along with arc e or er, but not in both implies feasibility of Step 5. All other steps are feasible saving arc capacities as in [26] in Step 6. Therefore, all the steps of Algorithm 1 are feasible. Second, we prove the optimality of the algorithm. By adding super source, a single-source single-sink extended network of reconfigured
optimally.Proof. The proof of the theorem consists of two steps. First, we show the feasibility. For this, we only have to show that Step 5 of the algorithm is feasible. Step 3 is feasible as shown in [21]. After applying Step 4 the flow is either along with arc e or er, but not in both implies feasibility of Step 5. All other steps are feasible saving arc capacities as in [26] in Step 6. Therefore, all the steps of Algorithm 1 are feasible. Second, we prove the optimality of the algorithm. By adding super source, a single-source single-sink extended network of reconfigured 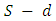 network is formed. Any optimal solution of the earliest arrival flow problem with lane reversal on network
network is formed. Any optimal solution of the earliest arrival flow problem with lane reversal on network 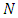 is also a feasible solution of the earliest arrival problem on the transformed network
is also a feasible solution of the earliest arrival problem on the transformed network 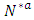 as in [21]. According to [3,21], we can compute minimum cost circulation on the transformed network
as in [21]. According to [3,21], we can compute minimum cost circulation on the transformed network 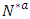 . The solution obtained in transformed network
. The solution obtained in transformed network 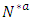 is the same as in the auxiliary network
is the same as in the auxiliary network 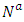 . As the optimal flow obtained is not changed and the capacity of unused arcs are saved, we can transform the solution to the original network. Thus, the earliest arrival flow on the transformed network is equal to the EAPCT for the original network
. As the optimal flow obtained is not changed and the capacity of unused arcs are saved, we can transform the solution to the original network. Thus, the earliest arrival flow on the transformed network is equal to the EAPCT for the original network 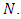 Corollary 1. The EAPCT with asymmetric capacity and transit time on arcs can be computed in polynomial-time complexity.Proof. The complexity of the algorithm is dominated by Steps 3 and 4. The remaining steps can be computed in linear time. The earliest arrival flow problem can be computed on the auxiliary network in polynomial-time in Step 3 according to [3,21]. This solution is equivalent to the earliest arrival contraflow problem on the given network. The flow can be decomposed in
Corollary 1. The EAPCT with asymmetric capacity and transit time on arcs can be computed in polynomial-time complexity.Proof. The complexity of the algorithm is dominated by Steps 3 and 4. The remaining steps can be computed in linear time. The earliest arrival flow problem can be computed on the auxiliary network in polynomial-time in Step 3 according to [3,21]. This solution is equivalent to the earliest arrival contraflow problem on the given network. The flow can be decomposed in 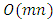 time in Step 4. Hence, the EAPCT with asymmetric capacity and transit time can be computed in polynomial-time.
time in Step 4. Hence, the EAPCT with asymmetric capacity and transit time can be computed in polynomial-time.4. LMPCF with Non-Symmetric Capacity and Transit Time
- Given an evacuation network
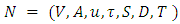 with non-symmetric capacity and transit time on each arc with fixed priority ordering at terminals, the LMPCF problem is to find a feasible dynamic flow at each priority terminal with arc reversals of only necessary capacities. The LMPCF problem with given supplies and demands at sources and sinks has been solved in polynomial-time [13,14]. However, if supplies and demands are unknown, then it is also solvable in the same complexity due to priority on terminals. In this section, we introduce LMPCF problem with non-symmetric capacity and transit time on
with non-symmetric capacity and transit time on each arc with fixed priority ordering at terminals, the LMPCF problem is to find a feasible dynamic flow at each priority terminal with arc reversals of only necessary capacities. The LMPCF problem with given supplies and demands at sources and sinks has been solved in polynomial-time [13,14]. However, if supplies and demands are unknown, then it is also solvable in the same complexity due to priority on terminals. In this section, we introduce LMPCF problem with non-symmetric capacity and transit time on 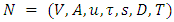 and present Algorithm 2 to solve Problem 2. The solution of LMPCF in the reconfigured network
and present Algorithm 2 to solve Problem 2. The solution of LMPCF in the reconfigured network 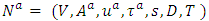 of Algorithm 2 is computed by calculating minimum cost flow in Step 2 by saving unused arc capacities after δ iterations within time horizon T.Problem 2. Given a multi-terminal network
of Algorithm 2 is computed by calculating minimum cost flow in Step 2 by saving unused arc capacities after δ iterations within time horizon T.Problem 2. Given a multi-terminal network 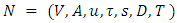 with terminals priority, the LMPCF problem with non-symmetric capacity and transit time is to find a feasible flow that lexicographically maximizes the amount of flow at each priority terminals if the arc direction can be reversed.Algorithm 2: The LMPCF algorithm with non-symmetric transit timeInput: Given a dynamic network
with terminals priority, the LMPCF problem with non-symmetric capacity and transit time is to find a feasible flow that lexicographically maximizes the amount of flow at each priority terminals if the arc direction can be reversed.Algorithm 2: The LMPCF algorithm with non-symmetric transit timeInput: Given a dynamic network 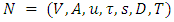 with constant and non-symmetric transit time.Output: An LMPCF1. Given network is transformed into the auxiliary network
with constant and non-symmetric transit time.Output: An LMPCF1. Given network is transformed into the auxiliary network 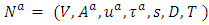 such that
such that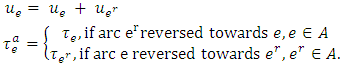 2. Compute lexicographic maximum flow on transformed network
2. Compute lexicographic maximum flow on transformed network 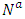 by using the algorithm of Hoppe and Tardos [14].3. Decompose the flow
by using the algorithm of Hoppe and Tardos [14].3. Decompose the flow 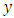 along paths and cycles and remove the flows in cycles.4. Reverse
along paths and cycles and remove the flows in cycles.4. Reverse 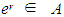 up to the capacity
up to the capacity 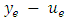 iff
iff 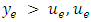 replaced by 0 whenever
replaced by 0 whenever 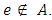 5. For each
5. For each 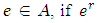 is reversed,
is reversed, 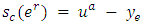 and
and 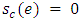 . If neither
. If neither 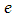 nor
nor 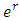 is reversed,
is reversed, 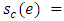
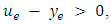 where
where 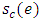 is the saved capacity of e.6. Transform the solution to the original network.Theorem 2. An optimal solution to LMPCF with non-symmetric capacity and transit time on arcs can be computed in polynomial-time.Proof. To prove the theorem, we have to prove the feasibility, optimality, and complexity of the algorithm. All steps of Algorithm 2 are feasible since Step 2 of the algorithm is feasible according to Hoppe and Tardos [14].Now, we prove the optimality of the algorithm. From the feasibility, any optimal solution of the LMPCF problem on network
is the saved capacity of e.6. Transform the solution to the original network.Theorem 2. An optimal solution to LMPCF with non-symmetric capacity and transit time on arcs can be computed in polynomial-time.Proof. To prove the theorem, we have to prove the feasibility, optimality, and complexity of the algorithm. All steps of Algorithm 2 are feasible since Step 2 of the algorithm is feasible according to Hoppe and Tardos [14].Now, we prove the optimality of the algorithm. From the feasibility, any optimal solution of the LMPCF problem on network 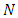 is also a feasible solution to the lexicographic flow problem on the corresponding auxiliary network
is also a feasible solution to the lexicographic flow problem on the corresponding auxiliary network 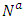 . An LMPCF problem can be solved in polynomial-time by using the algorithm of [14]. A temporally repeated lexicographic flow solution can be obtained optimally on the auxiliary network
. An LMPCF problem can be solved in polynomial-time by using the algorithm of [14]. A temporally repeated lexicographic flow solution can be obtained optimally on the auxiliary network 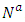 . Moreover, any optimal solution on
. Moreover, any optimal solution on 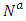 is equivalent to a feasible solution to given network
is equivalent to a feasible solution to given network 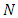 . The partial lane reversals approach saves the unused capacities of the arcs. Thus, the solution of the LMPCF on each arc of the network
. The partial lane reversals approach saves the unused capacities of the arcs. Thus, the solution of the LMPCF on each arc of the network  can be computed optimally.The complexity of Algorithm 2 is dominated by Steps 2. According to [14,19], Step 2 is solved in
can be computed optimally.The complexity of Algorithm 2 is dominated by Steps 2. According to [14,19], Step 2 is solved in 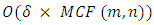 time, where
time, where 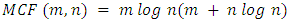 , the complexity of minimum cost flow problem. Since flow can be decomposed in
, the complexity of minimum cost flow problem. Since flow can be decomposed in 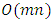 times and remaining steps can be solved in linear time
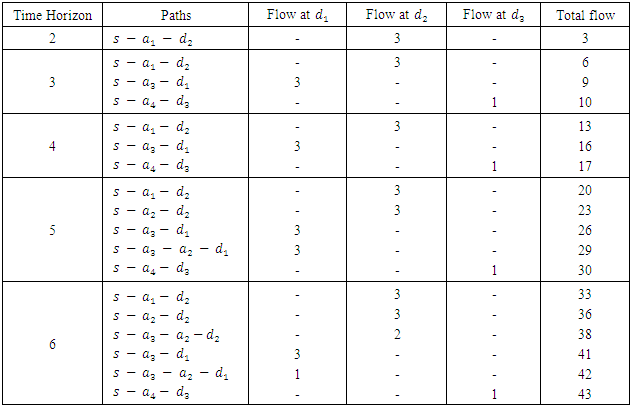
times and remaining steps can be solved in linear time 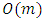 , the problem can be computed in polynomial-time complexity.Example 1. Consider a network with single source s and multiple sinks
, the problem can be computed in polynomial-time complexity.Example 1. Consider a network with single source s and multiple sinks 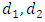 and
and 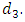 The first and second numbers on the arcs represent capacity and transit time on the arcs, respectively. We wish to find lexicographic maximum dynamic flow by giving priority to sinks, i.e.,
The first and second numbers on the arcs represent capacity and transit time on the arcs, respectively. We wish to find lexicographic maximum dynamic flow by giving priority to sinks, i.e., 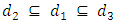 . The auxiliary network is shown in Figure 2.
. The auxiliary network is shown in Figure 2. 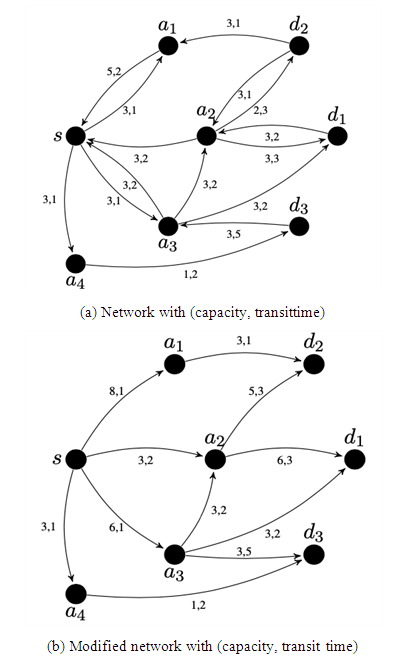 | Figure 2. (a) Two-way road network with arc capacity and transit time (b) Transformed network of (a) |
 , and arc having infinite capacity and transit time
, and arc having infinite capacity and transit time  from
from 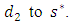 Joining an arc
Joining an arc 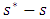 having infinite capacity and zero transit time and time horizon T = 6, we find minimum cost circulations.
having infinite capacity and zero transit time and time horizon T = 6, we find minimum cost circulations.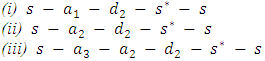 Choose minimum cost cycle
Choose minimum cost cycle 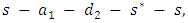 the feasible flow along this path is
the feasible flow along this path is 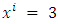 units. After sending 3 units flow along this path, we calculate the residual network. The next min-cost circulation cycle is
units. After sending 3 units flow along this path, we calculate the residual network. The next min-cost circulation cycle is 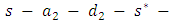
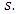 The feasible flow along this path is
The feasible flow along this path is 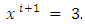 After sending 3 units flow along this path, again we calculate residual network. The next min-cost circulation cycle is
After sending 3 units flow along this path, again we calculate residual network. The next min-cost circulation cycle is 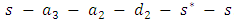 . The feasible flow along this path is
. The feasible flow along this path is 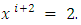 Now, there is no path from s to
Now, there is no path from s to 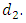 So, deleting the edge from
So, deleting the edge from 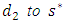 and adding the edge from the next priority sink, i.e.,
and adding the edge from the next priority sink, i.e., 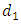 to super node
to super node 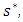 we repeat the same process until there is no path remaining from the source to any sinks. Hence the algorithm terminates with the lexicographic maximum flow as shown in Table 1.
we repeat the same process until there is no path remaining from the source to any sinks. Hence the algorithm terminates with the lexicographic maximum flow as shown in Table 1.
|
5. Conclusions
- The application of the contraflow approach in an existing transportation network has been increased during the last decades to save the lives of people and their property. The polynomial-time solution of contraflow problems with asymmetric capacity and symmetric transit time on arcs has been presented. Due to uneven road network topology, the maximum dynamic, earliest arrival contraflow problems with asymmetric capacity, and transit time on arcs has been studied. The contraflow problems with asymmetric transit time on lanes are the generalization of the problem with symmetric transit time and have the same time complexity. We introduced an EAPCT problem with asymmetric capacity and transit times on arcs and presented an algorithm to solve it in polynomial-time. During the evacuation, it is beneficial to assign priority to certain terminals to save the lives of injured people. So, we also extended this approach and presented a polynomial-time algorithm to solve LMPCF. As we have investigated the problems in single-commodity, we want to extend it for multi-commodity flow problems and generalized dynamic flow problems. Furthermore, we are interested in testing the performance of the algorithm by taking the real data set of the road network of Kathmandu metropolitan city.
Data Availability
- The authors have not used any additional data in this article.
Conflict of Interest
- The authors declare that they have no conflict of interests regarding the publication of this paper.
ACKNOWLEDGEMENTS
- The first author thanks the University Grants Commission (UGC), Nepal, for the Ph.D. research fellowship award 2018 with award no. PhD-074/75-S&T-10. We also thank the anonymous reviewers for their valuable comments and suggestions to improve the presentation of this paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML