Rasaki Olawale Olanrewaju1, Anthony Gichuhi Waititu2, Nafiu Lukman Abiodun3
1Pan African University, Institute for Basic Sciences, Technology and Innovation (PAUSTI), Kenya
2Department of Mathematical Sciences, Jomo Kenyatta University of Agriculture and Technology, Kenya
3Department of Mathematics and Statistics, Kabale University, Kabale, Uganda
Correspondence to: Rasaki Olawale Olanrewaju, Pan African University, Institute for Basic Sciences, Technology and Innovation (PAUSTI), Kenya.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper describes Fréchet distribution as a random noise for capturing multimodalities, regime-switching and change-points attributed to uniformly time-varying series via causality of fluctuations, extreme values and heavy-tailed time series. Fréchet Mixture Autoregressive (FMAR) model of k-regime-switching, denoted by 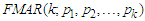 was developed and Expectation-Maximization (EM) algorithm was used as a method of parameter estimation for the embedded coefficients of AR of k-mixing weights and lag pk. The limiting distribution of the
was developed and Expectation-Maximization (EM) algorithm was used as a method of parameter estimation for the embedded coefficients of AR of k-mixing weights and lag pk. The limiting distribution of the 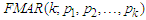 model via Gnedenko-Fisher Tippet limiting property was derived to asymptotically approach an exponential function.
model via Gnedenko-Fisher Tippet limiting property was derived to asymptotically approach an exponential function.
Keywords:
Fréchet distribution, Expectation-Maximization, Gnedenko-Fisher Tippet, k-regime-switching, Mixture Autoregressive, Multimodalities
Cite this paper: Rasaki Olawale Olanrewaju, Anthony Gichuhi Waititu, Nafiu Lukman Abiodun, Fréchet Random Noise for k-Regime-Switching Mixture Autoregressive Model, American Journal of Mathematics and Statistics, Vol. 11 No. 1, 2021, pp. 1-10. doi: 10.5923/j.ajms.20211101.01.
1. Introduction
Some of the problems of time series are cyclical fluctuation and regime-switching, full range of shape changing predictive distributions (multimodalities), change like behavior and inability to handle cycles traits that were characterized by the data series [2]. Some non-linear time series models such as Threshold Auto-Regressive (TAR), and Self Exciting Threshold Autoregressive (SETAR) were proposed contain the made mentioned stylized properties, but were limited to two regime-shifting [8]. Mixture Autoregressive (MAR) model 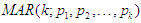 proposed by [14] captured and modeled the aforementioned stylized traits with strictly Gaussian or normal distributed error term. The problem of regime-switching model via mixture models are yet to be fully and completely addressed by
proposed by [14] captured and modeled the aforementioned stylized traits with strictly Gaussian or normal distributed error term. The problem of regime-switching model via mixture models are yet to be fully and completely addressed by 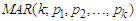 model with Gaussian random noise [1].According to [4], structural
model with Gaussian random noise [1].According to [4], structural 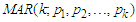 time-series model has been statistically deficiency due to inadequate to take into consideration multimodalities, large fluctuations, heavy-tail and non-Gaussian distributional random noise that are causal traits of the multimodalities and tenure-changing. However, the MAR model with Gaussian marginal distribution is noted to inadequately capture extreme events that are usually the causal of distortion that leads to multimodalities and tenure-changing [7]. Consequently, the stated problem of MAR model with Gaussian error term would be addressed by Fréchet random noise, being one of the three Extreme Value Distributions (EVDs). In other words, Fréchet Mixture Autoregressive
time-series model has been statistically deficiency due to inadequate to take into consideration multimodalities, large fluctuations, heavy-tail and non-Gaussian distributional random noise that are causal traits of the multimodalities and tenure-changing. However, the MAR model with Gaussian marginal distribution is noted to inadequately capture extreme events that are usually the causal of distortion that leads to multimodalities and tenure-changing [7]. Consequently, the stated problem of MAR model with Gaussian error term would be addressed by Fréchet random noise, being one of the three Extreme Value Distributions (EVDs). In other words, Fréchet Mixture Autoregressive 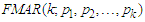 model with Fréchet error term will be developed and derived as a substitute for MAR to capture extreme events (outliers) that are causes of large fluctuations in arising due to abnormal kurtosis and skewness. Hence, this article develops, ascertains and estimates embedded parameters (AR coefficients, mixing weights and Fréchet coefficients) via Expectation-Maximization algorithm of the
model with Fréchet error term will be developed and derived as a substitute for MAR to capture extreme events (outliers) that are causes of large fluctuations in arising due to abnormal kurtosis and skewness. Hence, this article develops, ascertains and estimates embedded parameters (AR coefficients, mixing weights and Fréchet coefficients) via Expectation-Maximization algorithm of the 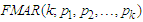 process with k-regime-switching. In addition, the limiting distribution (asymptotic property) of the
process with k-regime-switching. In addition, the limiting distribution (asymptotic property) of the 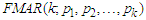 model will be ascertained via Gnedenko-Fisher Tippet limiting behavior as well as the ergodic of the FMA process. The mean and variance of the
model will be ascertained via Gnedenko-Fisher Tippet limiting behavior as well as the ergodic of the FMA process. The mean and variance of the 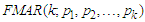 process will be ascertained as well.
process will be ascertained as well.
2. Literature Review
The history of mixture time series model was originated and propounded by [15] in the late 1900s, when he used normal mixture to model outliers and employ the method of moments to decompose normal mixtures. He deduced that Autoregressive Integrated Moving Average (ARIMA), Self-Exciting Threshold Autoregressive (SETAR) model, and other nonlinear models can only depict a unimodal predictive time series random noise distribution. He affirmed that mixture model would be needed for stylist, cyclical, switching tenure properties to be revealed. Afterwards, [3] predicted with the MAR model and deduced that MAR model possessed the attractive property in such a way that spatial attributes of the conditional density of its prediction contingents upon on the immediate past events of the process. Additionally, he maintained that the multiple steps’ distribution would be a collection (mixture) of normal distributions if and only if the source MAR model is a mixture of normal densities.However, despite propounded of all these models, no model studied the stationarity and ergodicity traits of MAR related models. It was in line of this deficiency that [8] propounded and affirmed the theoretical advantage of Gaussian mixture autoregressive (GMAR) conditions for stationarity and ergodicity to be met. They claimed that GMAR properties were straightforward to establish. In addition, they maintained that pth order model can be explicitly expressed in a (Optimal order (p) +1)– lengthy stationary distribution with ascertained constant mixing weights to connote mixture of normal probability distributions.In advancement, [7] proposed a novel nonlinear Vector Autoregressive (VAR) otherwise called Gaussian Mixture Vector autoregressive (GMVAR) model. They developed and explained its asymptotic theory of maximum likelihood whose usefulness is vital when dealing with bivariate time series settings.Furthermore, [6] proposed a new nonlinear time series via a vector incorporation into the MAR model called Vector-MAR (VAR) model otherwise known as Gaussian Mixture Vector Autoregressive (GMVAR) model. They affirmed and claimed that the GMVAR model can be categorized as member of the mixture VAR models because of its normally distributed error term, constructed and developed for studying nonlinear models with time-varying series that exhibited tenure changing traits. They maintained that primarily the GMVAR model differs from the variety of VAR models in the meaning of the mingling proportions that regularize the tenure likelihoods. [11] provided an up-to-date theoretical and methodological developments on finite mixture models due to its flexibility increasingly exploitation and applications. They adopted the semiparametric technique way of parameter estimation via the EM algorithm to carve out the distributional shape changing, group-structure and cluster analysis in the data captured to the model. Proposed models reviewed were formulated to capture, and correct the stylized properties; entire outrange of pattern switching distributions (multimodalities), change points like behavior, regime switching (capable of handling recurring periodical sequence), and time-varying volatilities (conditional means-variances), but no method/model yet to cater for heavy-tailed, long-memory and non-Gaussian MAR model. Hence, a full sketch 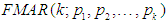 model will be developed such that its mean and variance will as ascertained as well as its parameter estimation, limiting distribution and ergodic process.
model will be developed such that its mean and variance will as ascertained as well as its parameter estimation, limiting distribution and ergodic process.
3. Specification of the Fréchet Mixture Autoregressive Model
[10] and [13] defined a k-component of Mixture Autoregressive (MAR) model 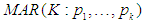 to be
to be 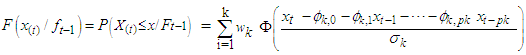 | (1) |
Rewriting the k-component of MAR model in (1) in Fréchet Mixture Autoregressive 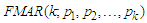 gives
gives 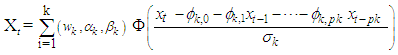 | (2) |
where; 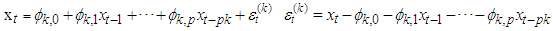
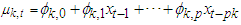 Otherwise,
Otherwise,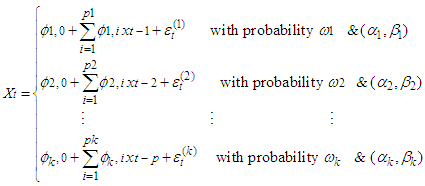 | (3) |
Where, 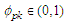 , for
, for  . For mixing weights
. For mixing weights 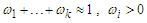 , for
, for 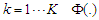 is the Cumulative Distribution Function of the standard distributions, where
is the Cumulative Distribution Function of the standard distributions, where 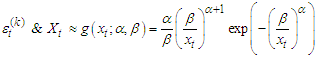 , with mean
, with mean 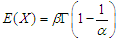 and variance
and variance 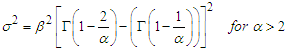 .
.
3.1. The Conditional Mean and Variance for FMA Model
The conditional mean and variance for FMA model of 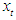 given the previous preceding values is as follow:
given the previous preceding values is as follow: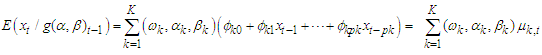 | (4) |
since, 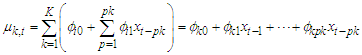 The mean of Fréchet is
The mean of Fréchet is 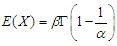 , therefore
, therefore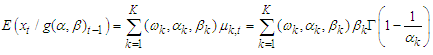 | (5) |
which relies on previous preceding values of the time series &  is the PDF of Fréchet.
is the PDF of Fréchet.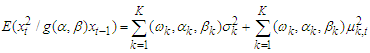 So,
So, 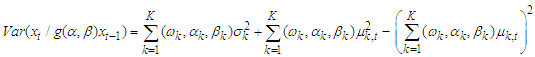 But,
But, 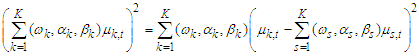 for
for  (previous preceding values of the time series that relies on
(previous preceding values of the time series that relies on  the current values).
the current values).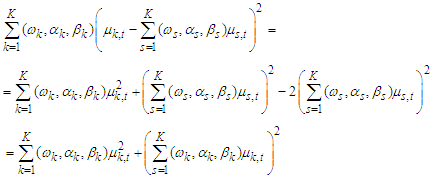 Therefore,
Therefore, 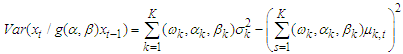 | (6) |
The expression 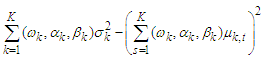 is a positive quantity. Hence, this meets the non-negative property of variance.Since the mean and variance of Fréchet PDF are;
is a positive quantity. Hence, this meets the non-negative property of variance.Since the mean and variance of Fréchet PDF are; 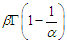 and
and 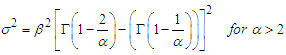 respectivelyAlternatively,
respectivelyAlternatively, 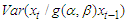 of equation (6) can be written as
of equation (6) can be written as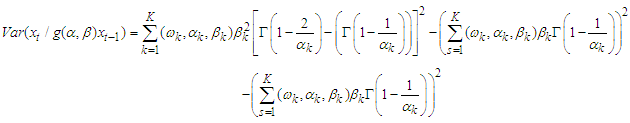 | (7) |
3.2. Parameter Estimation for FMA via EM Algorithm
Adopting the Expectation-Maximization (EM) algorithm propounded by [10] for non-linear and regime-switching. Let 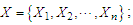
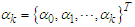
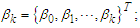
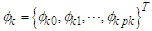
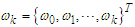 for
for 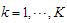 Additionally, supposing that “S” is the unobserved random variable where
Additionally, supposing that “S” is the unobserved random variable where 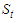 is a
is a 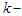 dimensional vector such that
dimensional vector such that 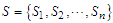
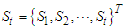 whose component is
whose component is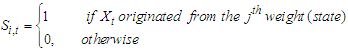 For
For 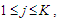 that is, Let
that is, Let 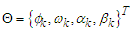 be the universal space of parameters.Given
be the universal space of parameters.Given 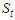 , the Fréchet distribution of the complete data
, the Fréchet distribution of the complete data 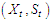 is given by
is given by 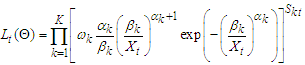 | (8) |
If 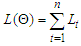 is the log-likelihood. Letting
is the log-likelihood. Letting 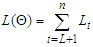 be the joint conditional log-likelihood function for large sample size (n) for maximizing the function gives
be the joint conditional log-likelihood function for large sample size (n) for maximizing the function gives 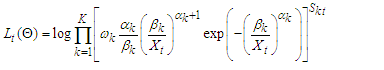 | (9) |
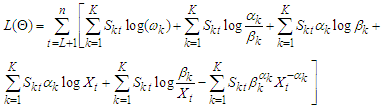 | (10) |
Where 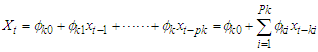 First derivatives of
First derivatives of 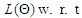 each of the parameter gives,
each of the parameter gives,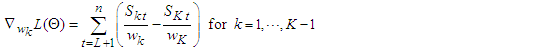 | (11) |
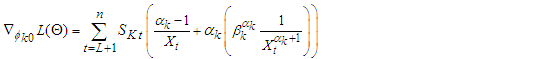 | (12) |
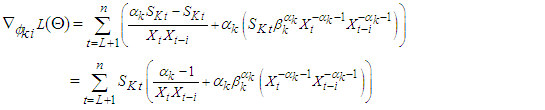 | (13) |
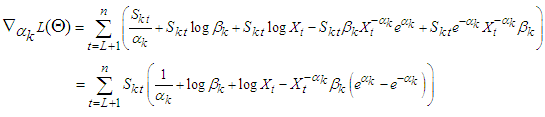 | (14) |
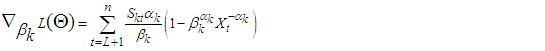 | (15) |
For 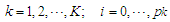 Then, the second derivatives of individual coefficient estimated from (11) - (15) depends of setting a function
Then, the second derivatives of individual coefficient estimated from (11) - (15) depends of setting a function 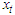 to be a random variable at time
to be a random variable at time 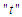 and counter
and counter 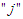
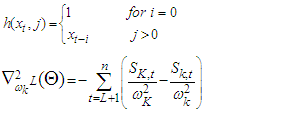 | (16) |
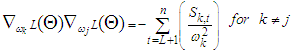 | (17) |
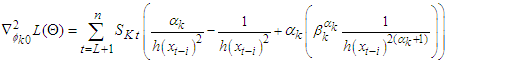 | (18) |
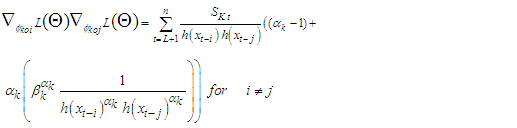 | (19) |
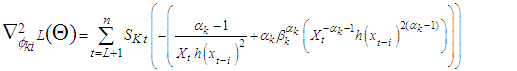 | (20) |
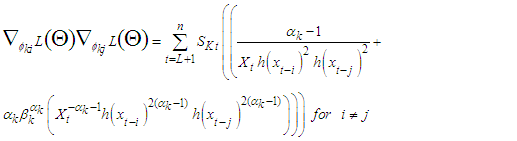 | (21) |
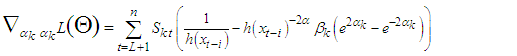 | (22) |
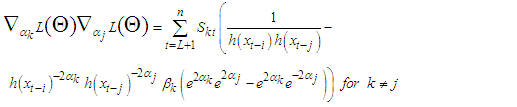 | (23) |
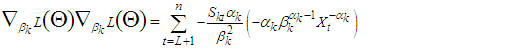 | (24) |
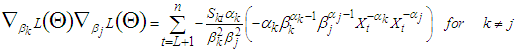 | (25) |
Adopting the EM algorithm for estimating the parameter space 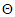 in
in 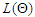 of (10).(a) The first step of the Expectation-Maximization algorithm which stands for E-step, If each of the coefficient (parameter) in the parameter space
of (10).(a) The first step of the Expectation-Maximization algorithm which stands for E-step, If each of the coefficient (parameter) in the parameter space 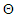 is known, such that the unknown values of the unobserved data
is known, such that the unknown values of the unobserved data 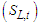 is then substituted by enforcing their means on each coefficient on the observed data Xt. Subjecting
is then substituted by enforcing their means on each coefficient on the observed data Xt. Subjecting 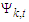 has the enforced mean on
has the enforced mean on 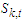 , then the individual probability of
, then the individual probability of 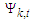 is the total probability of the enforced means over individual mean, as given in equation below:
is the total probability of the enforced means over individual mean, as given in equation below: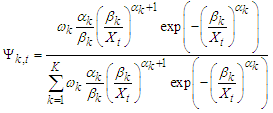 | (26) |
For 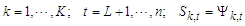 (b) The M-step where the unknown values of S is presumed via guessing and their enforced means are assumed to be the coefficients. The mixing weight per each regime is then estimate via
(b) The M-step where the unknown values of S is presumed via guessing and their enforced means are assumed to be the coefficients. The mixing weight per each regime is then estimate via 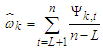 | (27) |
For 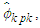 where
where 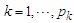 such that the estimates of parameters of these two steps are iterated until convergence is reached. The criterion for checking convergence was obtained by [12] as,
such that the estimates of parameters of these two steps are iterated until convergence is reached. The criterion for checking convergence was obtained by [12] as,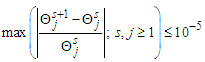 | (28) |
for 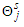 being the jth component of
being the jth component of 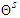 .
.
3.3. Limiting Distribution (Asymptotic Property) for FMA Model
The Limit distribution (Asymptotic property) for FMA model would be based on limiting laws for Extreme Value Distributions stated by Gnedenko-Fisher Tippet theorem [9]. The theorem stated that: Let 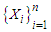 be a sequence of IID random variables of sample size (n) with common Cumulative Density Function
be a sequence of IID random variables of sample size (n) with common Cumulative Density Function 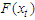 with its maximum denoted as
with its maximum denoted as 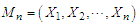 such that distribution (Limiting behavior ) of
such that distribution (Limiting behavior ) of 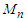 as the sample size (n) approaches infinity is
as the sample size (n) approaches infinity is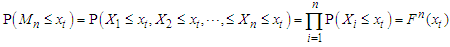 Investigating the wavering of
Investigating the wavering of 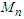 in a similar vein to that of Central Limit Theorem (CTL) for sum of the random variables
in a similar vein to that of Central Limit Theorem (CTL) for sum of the random variables 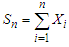 , then the distribution of
, then the distribution of 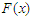 belongs to the maximum domain of non-degenerate distribution
belongs to the maximum domain of non-degenerate distribution 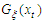 if there exist sequences of constants
if there exist sequences of constants 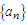 and
and 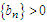 , such there exist a real value
, such there exist a real value 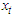 for
for 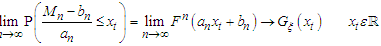 .Such that
.Such that 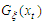 is non-degenerate distribution function, and
is non-degenerate distribution function, and 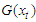 belongs to any of the
belongs to any of the 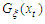 Starting with,
Starting with, 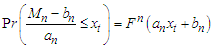 the Cumulative Distribution Function for Fréchet is
the Cumulative Distribution Function for Fréchet is 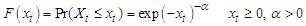 | (29) |
So, 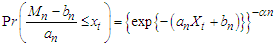 | (30) |
Where, 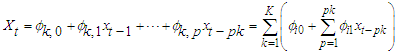
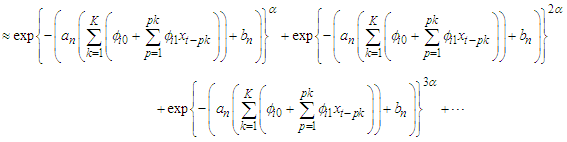 | (31) |
According to [5], the normalizing constants of 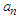 and
and 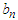 for Fréchet distribution are approximately
for Fréchet distribution are approximately 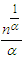 and
and 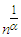 respectively, where
respectively, where 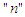 is the set of natural numbers.
is the set of natural numbers.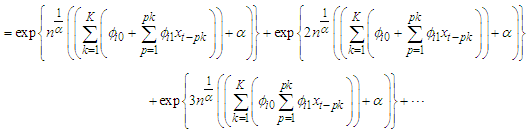 | (32) |
Logarithm of both sides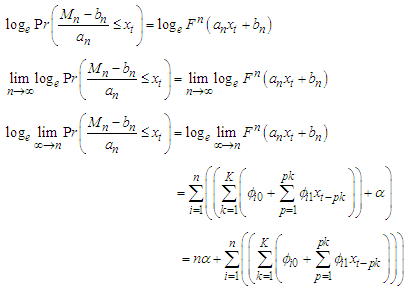 | (33) |
Taking exponent of both sides so as to naturalize the logarithm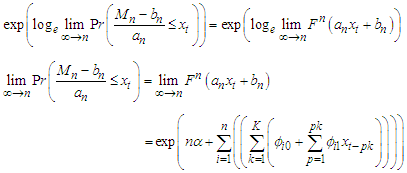 | (34) |
Which means that as 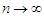 , the limiting distribution of the FMA asymptotically approaches
, the limiting distribution of the FMA asymptotically approaches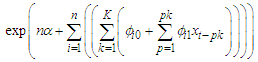
3.4. Ergodic Process for FMA Model
Strictly stationary and ergodic processes for FMA model would be ascertained via 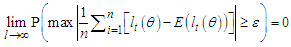 Where,
Where, 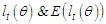 are likelihoods and expectations of likelihoods respectively.
are likelihoods and expectations of likelihoods respectively.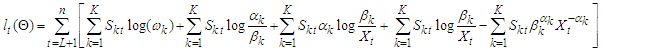 | (35) |
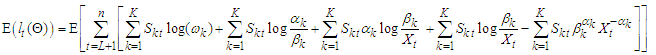 | (36) |
But,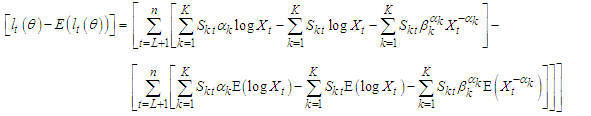 | (37) |
From Jensen’s inequality, 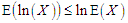 for every positively integrable X.
for every positively integrable X.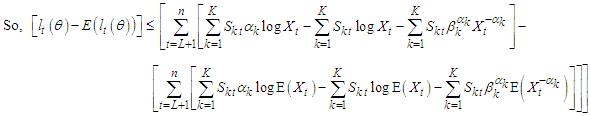 | (38) |
Recall, 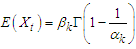
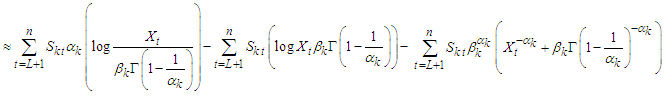 | (39) |
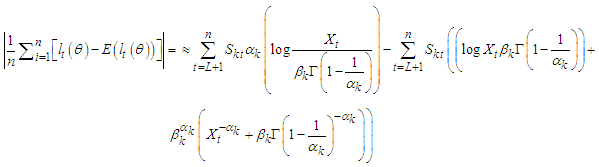 | (40) |
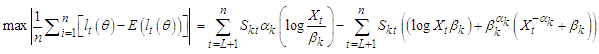 | (41) |
since, 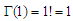
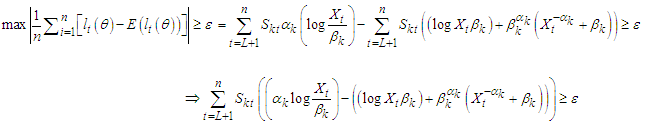 | (42) |
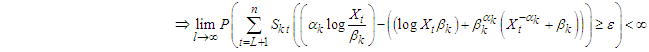 | (43) |
4. Conclusions
The proposed model of 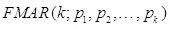 being one of the prominent models for extreme valued mixture autoregressive was devised in order to sieze and objurgate stylized traits; entire greater range of multimodalities, regime-switching, (ability to handle cycles), time-varying volatilities (conditional variances), time-varying mixing weights with Fréchet Probability Density Function (PDF). Long-memory, heavy-tailed distributed observations are the causal that arise to outliers, change points like behavior, abnormal kurtosis, and skewness. The formulated and proposed
being one of the prominent models for extreme valued mixture autoregressive was devised in order to sieze and objurgate stylized traits; entire greater range of multimodalities, regime-switching, (ability to handle cycles), time-varying volatilities (conditional variances), time-varying mixing weights with Fréchet Probability Density Function (PDF). Long-memory, heavy-tailed distributed observations are the causal that arise to outliers, change points like behavior, abnormal kurtosis, and skewness. The formulated and proposed 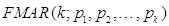 will be an ideal and substitute mixture autoregressive model whenever heavy-tailed distributed observations are the causal that arise to outliers, abnormal kurtosis, and skewness brings about the regime-switching.
will be an ideal and substitute mixture autoregressive model whenever heavy-tailed distributed observations are the causal that arise to outliers, abnormal kurtosis, and skewness brings about the regime-switching.
ACKNOWLEDGEMENTS
We wish to acknowledge Africa Union for funding this research as well as reviewers.
References
| [1] | A. Ang, and A. Timmermann, “Regime Changes and Financial Markets” Annual Review of Financial Economics, Vol. 4(1), pp. 313-337, 2011. |
| [2] | G. Behrooz., S.M.N. Abu Hassan, and S. Tamat, “Application of the Threshold Model for Modelling and Forecasting of Exchange Rate in Selected ASEAN Countries”. Sains Malaysiana, Vol.43(10), pp. 1609-1622, 2014. |
| [3] | G.N. Boshankov, “Prediction with Mixture Autoregressive Models” Research Report No.6, 2006, Probability and Statistics Group School of Mathematics. The University of Manchester, 2006. |
| [4] | T.A. Chawsheen, and M. Broom, “Seasonal time-series modeling and forecasting of monthly mean temperature for decision making in the Kurdistan Region of Iraq”. Journal of Statistical Theory and Practice. Vol. 11(4), pp.604– 633, 2017. |
| [5] | J. Y. Fortin, and M. Clusel, “Applications of extreme value statistics in physics”. Journal of Physics, A Mathematical and Theoretical, pp. 1-39, 2015. |
| [6] | L. Kalliovirta, M. Meitz, and P. Saikkonen., “Identification and estimation of non-Gaussian Structural Vector Autoregressions” Journal of Econometric, Vol. 196, pp. 288-304, 2017. |
| [7] | L. Kalliovirta, M. Meitz, and P. Saikkonen, A Guassian Mixture Vector Autoregressive. Journal of econometrics, Vol.192, pp. 485-498, 2016. |
| [8] | L. Kalliovirta, M. Meitz, P. and Saikkonen, “A Guassian Mixture autoregresive model for univariate series” Journal of Time Series Analysis, Vol. 36, pp. 247-266, 2012. |
| [9] | O. Karpa, “Development of Bivariate Extreme Value Distributions for Applications in Marine Technology”. (Doctoral thesis, Norwegian University of Science and Technology (NTNU), Norway), 2015. |
| [10] | M. Li, and M. Raftery, “Modeling flat stretches, burst and outliers in time series using Mixture Transition Distribution Models”. Journal of American Statistics Association, Vol. 91, pp.1504-1514, 1966. |
| [11] | G.J. McLachlan, S.X. Lee, and I. R. Suren. Finite Mixture Models. Annual Review of Statistics and Its Application Finite Mixture Models, Vol. 6, pp. 355–378, 2019. |
| [12] | V. Melnykova, and I. Melnykovb “Initializing the EM algorithm in gaussian mixture models with an unknown number of components” Computational Statistics and Data Analysis, Vol. 56, pp. 1381–1395, 2012. |
| [13] | N. Nguyen, “Hidden Markov Model for Stock Trading”. International Journal Financial studies, Vol. 6 (36), 2018. |
| [14] | C.S. Wong, W.S, Chan, and P.L. Kam, “A student t-Mixture Autoregressive Model with Application to heavy-tailed financial data” Singapore Economic Review Conference, pp. 1-10, 2009. |
| [15] | C. S. Wong, “Statistical inference for some nonlinear time series models” Ph.D thesis, University of Hong Kong, Hong Kong, 1998. |


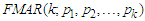 was developed and Expectation-Maximization (EM) algorithm was used as a method of parameter estimation for the embedded coefficients of AR of k-mixing weights and lag pk. The limiting distribution of the
was developed and Expectation-Maximization (EM) algorithm was used as a method of parameter estimation for the embedded coefficients of AR of k-mixing weights and lag pk. The limiting distribution of the 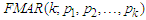 model via Gnedenko-Fisher Tippet limiting property was derived to asymptotically approach an exponential function.
model via Gnedenko-Fisher Tippet limiting property was derived to asymptotically approach an exponential function.
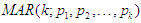 proposed by [14] captured and modeled the aforementioned stylized traits with strictly Gaussian or normal distributed error term. The problem of regime-switching model via mixture models are yet to be fully and completely addressed by
proposed by [14] captured and modeled the aforementioned stylized traits with strictly Gaussian or normal distributed error term. The problem of regime-switching model via mixture models are yet to be fully and completely addressed by 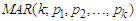 model with Gaussian random noise [1].According to [4], structural
model with Gaussian random noise [1].According to [4], structural 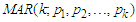 time-series model has been statistically deficiency due to inadequate to take into consideration multimodalities, large fluctuations, heavy-tail and non-Gaussian distributional random noise that are causal traits of the multimodalities and tenure-changing. However, the MAR model with Gaussian marginal distribution is noted to inadequately capture extreme events that are usually the causal of distortion that leads to multimodalities and tenure-changing [7]. Consequently, the stated problem of MAR model with Gaussian error term would be addressed by Fréchet random noise, being one of the three Extreme Value Distributions (EVDs). In other words, Fréchet Mixture Autoregressive
time-series model has been statistically deficiency due to inadequate to take into consideration multimodalities, large fluctuations, heavy-tail and non-Gaussian distributional random noise that are causal traits of the multimodalities and tenure-changing. However, the MAR model with Gaussian marginal distribution is noted to inadequately capture extreme events that are usually the causal of distortion that leads to multimodalities and tenure-changing [7]. Consequently, the stated problem of MAR model with Gaussian error term would be addressed by Fréchet random noise, being one of the three Extreme Value Distributions (EVDs). In other words, Fréchet Mixture Autoregressive 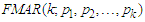 model with Fréchet error term will be developed and derived as a substitute for MAR to capture extreme events (outliers) that are causes of large fluctuations in arising due to abnormal kurtosis and skewness. Hence, this article develops, ascertains and estimates embedded parameters (AR coefficients, mixing weights and Fréchet coefficients) via Expectation-Maximization algorithm of the
model with Fréchet error term will be developed and derived as a substitute for MAR to capture extreme events (outliers) that are causes of large fluctuations in arising due to abnormal kurtosis and skewness. Hence, this article develops, ascertains and estimates embedded parameters (AR coefficients, mixing weights and Fréchet coefficients) via Expectation-Maximization algorithm of the 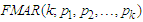 process with k-regime-switching. In addition, the limiting distribution (asymptotic property) of the
process with k-regime-switching. In addition, the limiting distribution (asymptotic property) of the 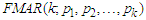 model will be ascertained via Gnedenko-Fisher Tippet limiting behavior as well as the ergodic of the FMA process. The mean and variance of the
model will be ascertained via Gnedenko-Fisher Tippet limiting behavior as well as the ergodic of the FMA process. The mean and variance of the 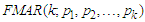 process will be ascertained as well.
process will be ascertained as well.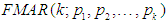 model will be developed such that its mean and variance will as ascertained as well as its parameter estimation, limiting distribution and ergodic process.
model will be developed such that its mean and variance will as ascertained as well as its parameter estimation, limiting distribution and ergodic process.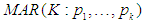 to be
to be 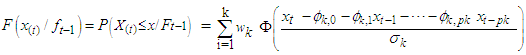
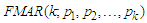 gives
gives 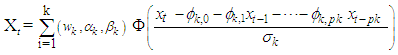
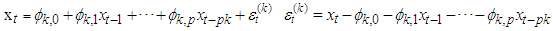
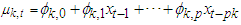 Otherwise,
Otherwise,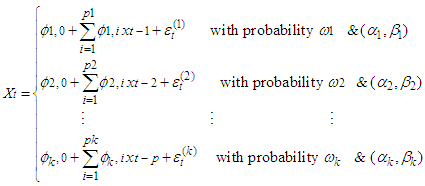
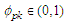 , for
, for 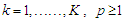 . For mixing weights
. For mixing weights 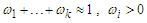 , for
, for 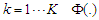 is the Cumulative Distribution Function of the standard distributions, where
is the Cumulative Distribution Function of the standard distributions, where 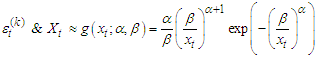 , with mean
, with mean 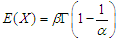 and variance
and variance 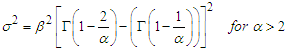 .
.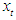 given the previous preceding values is as follow:
given the previous preceding values is as follow: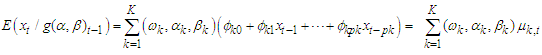
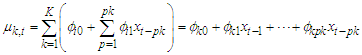 The mean of Fréchet is
The mean of Fréchet is 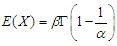 , therefore
, therefore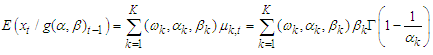
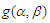 is the PDF of Fréchet.
is the PDF of Fréchet.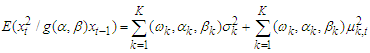 So,
So, 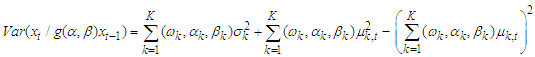 But,
But, 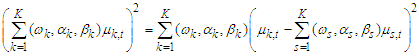 for
for 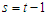 (previous preceding values of the time series that relies on
(previous preceding values of the time series that relies on 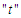 the current values).
the current values).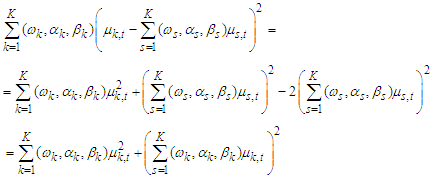 Therefore,
Therefore, 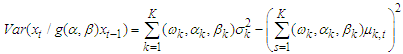
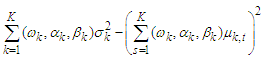 is a positive quantity. Hence, this meets the non-negative property of variance.Since the mean and variance of Fréchet PDF are;
is a positive quantity. Hence, this meets the non-negative property of variance.Since the mean and variance of Fréchet PDF are; 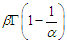 and
and 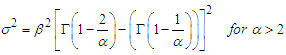 respectivelyAlternatively,
respectivelyAlternatively, 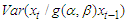 of equation (6) can be written as
of equation (6) can be written as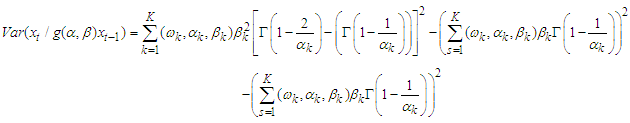
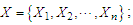
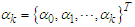
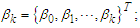
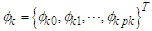
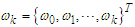 for
for 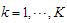 Additionally, supposing that “S” is the unobserved random variable where
Additionally, supposing that “S” is the unobserved random variable where 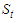 is a
is a 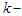 dimensional vector such that
dimensional vector such that 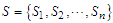
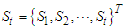 whose component is
whose component is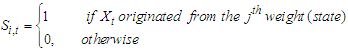 For
For 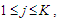 that is, Let
that is, Let 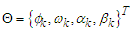 be the universal space of parameters.Given
be the universal space of parameters.Given 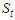 , the Fréchet distribution of the complete data
, the Fréchet distribution of the complete data 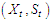 is given by
is given by 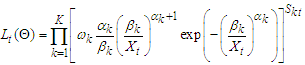
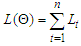 is the log-likelihood. Letting
is the log-likelihood. Letting 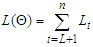 be the joint conditional log-likelihood function for large sample size (n) for maximizing the function gives
be the joint conditional log-likelihood function for large sample size (n) for maximizing the function gives 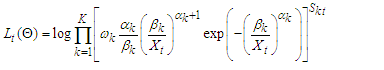
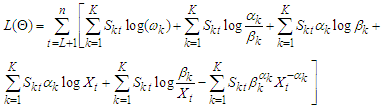
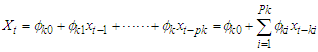 First derivatives of
First derivatives of 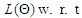 each of the parameter gives,
each of the parameter gives,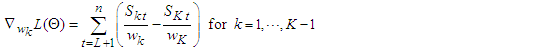
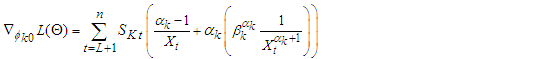
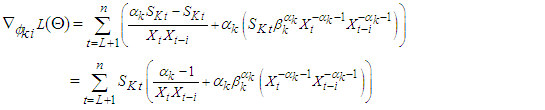
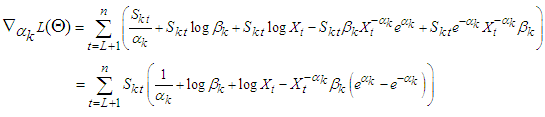
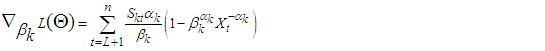
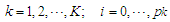 Then, the second derivatives of individual coefficient estimated from (11) - (15) depends of setting a function
Then, the second derivatives of individual coefficient estimated from (11) - (15) depends of setting a function 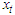 to be a random variable at time
to be a random variable at time 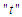 and counter
and counter 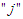
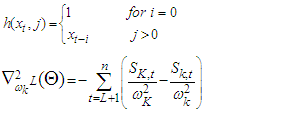
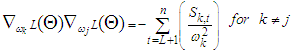
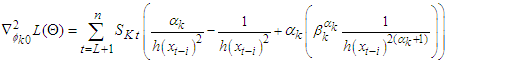
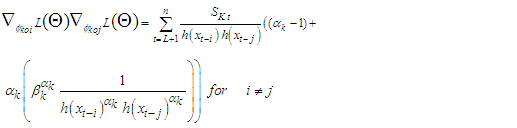
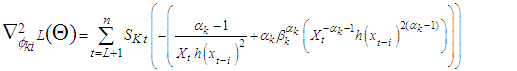
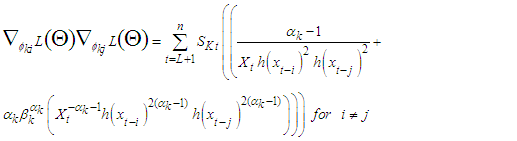
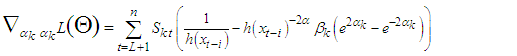
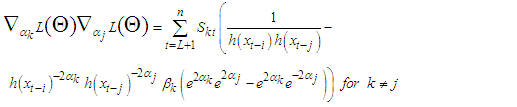
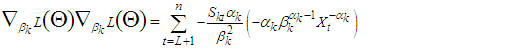
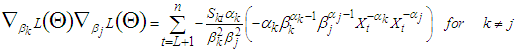
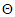 in
in 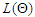 of (10).(a) The first step of the Expectation-Maximization algorithm which stands for E-step, If each of the coefficient (parameter) in the parameter space
of (10).(a) The first step of the Expectation-Maximization algorithm which stands for E-step, If each of the coefficient (parameter) in the parameter space 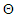 is known, such that the unknown values of the unobserved data
is known, such that the unknown values of the unobserved data 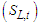 is then substituted by enforcing their means on each coefficient on the observed data Xt. Subjecting
is then substituted by enforcing their means on each coefficient on the observed data Xt. Subjecting 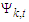 has the enforced mean on
has the enforced mean on 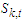 , then the individual probability of
, then the individual probability of 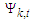 is the total probability of the enforced means over individual mean, as given in equation below:
is the total probability of the enforced means over individual mean, as given in equation below: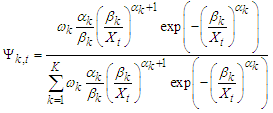
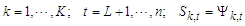 (b) The M-step where the unknown values of S is presumed via guessing and their enforced means are assumed to be the coefficients. The mixing weight per each regime is then estimate via
(b) The M-step where the unknown values of S is presumed via guessing and their enforced means are assumed to be the coefficients. The mixing weight per each regime is then estimate via 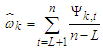
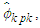 where
where 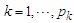 such that the estimates of parameters of these two steps are iterated until convergence is reached. The criterion for checking convergence was obtained by [12] as,
such that the estimates of parameters of these two steps are iterated until convergence is reached. The criterion for checking convergence was obtained by [12] as,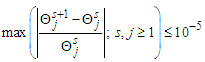
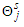 being the jth component of
being the jth component of 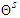 .
.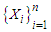 be a sequence of IID random variables of sample size (n) with common Cumulative Density Function
be a sequence of IID random variables of sample size (n) with common Cumulative Density Function 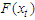 with its maximum denoted as
with its maximum denoted as 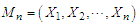 such that distribution (Limiting behavior ) of
such that distribution (Limiting behavior ) of 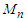 as the sample size (n) approaches infinity is
as the sample size (n) approaches infinity is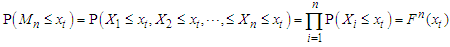 Investigating the wavering of
Investigating the wavering of 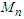 in a similar vein to that of Central Limit Theorem (CTL) for sum of the random variables
in a similar vein to that of Central Limit Theorem (CTL) for sum of the random variables 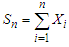 , then the distribution of
, then the distribution of 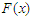 belongs to the maximum domain of non-degenerate distribution
belongs to the maximum domain of non-degenerate distribution 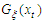 if there exist sequences of constants
if there exist sequences of constants 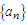 and
and 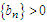 , such there exist a real value
, such there exist a real value 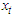 for
for 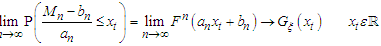 .Such that
.Such that 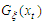 is non-degenerate distribution function, and
is non-degenerate distribution function, and 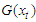 belongs to any of the
belongs to any of the 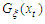 Starting with,
Starting with, 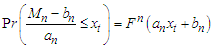 the Cumulative Distribution Function for Fréchet is
the Cumulative Distribution Function for Fréchet is 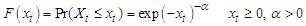
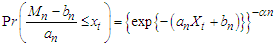
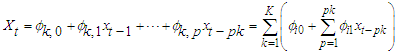
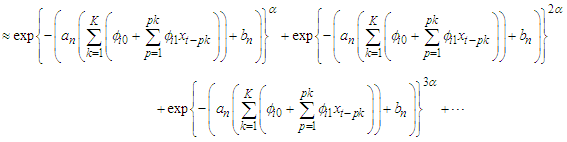
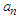 and
and 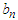 for Fréchet distribution are approximately
for Fréchet distribution are approximately 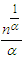 and
and 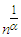 respectively, where
respectively, where 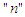 is the set of natural numbers.
is the set of natural numbers.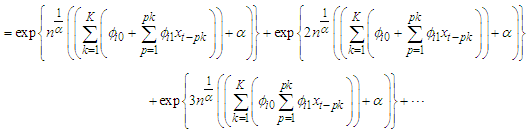
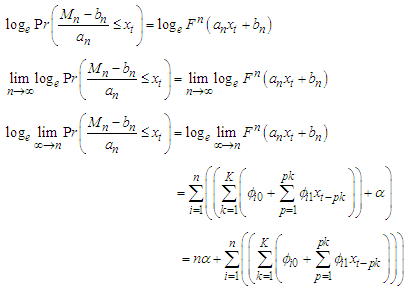
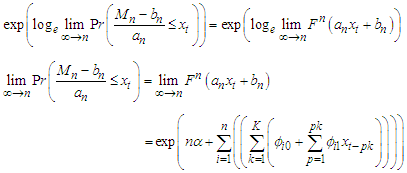
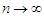 , the limiting distribution of the FMA asymptotically approaches
, the limiting distribution of the FMA asymptotically approaches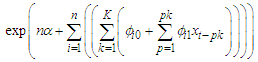
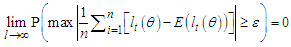 Where,
Where, 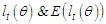 are likelihoods and expectations of likelihoods respectively.
are likelihoods and expectations of likelihoods respectively.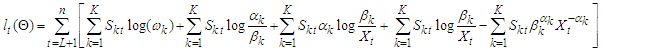
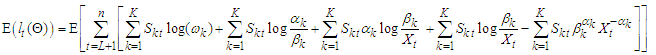
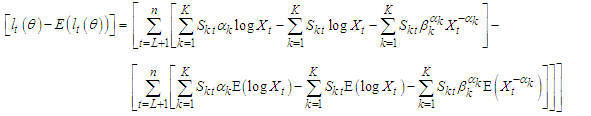
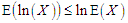 for every positively integrable X.
for every positively integrable X.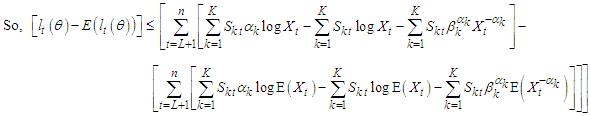
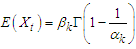
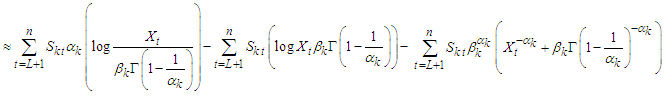
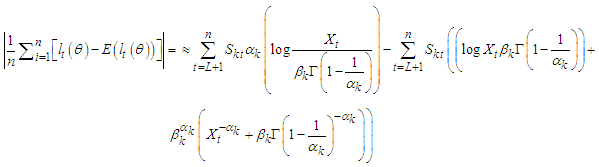
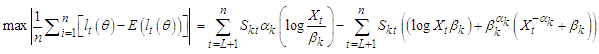
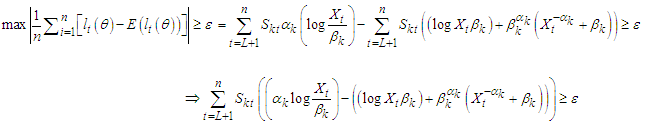
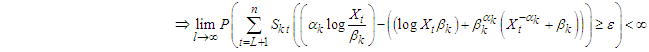
 being one of the prominent models for extreme valued mixture autoregressive was devised in order to sieze and objurgate stylized traits; entire greater range of multimodalities, regime-switching, (ability to handle cycles), time-varying volatilities (conditional variances), time-varying mixing weights with Fréchet Probability Density Function (PDF). Long-memory, heavy-tailed distributed observations are the causal that arise to outliers, change points like behavior, abnormal kurtosis, and skewness. The formulated and proposed
being one of the prominent models for extreme valued mixture autoregressive was devised in order to sieze and objurgate stylized traits; entire greater range of multimodalities, regime-switching, (ability to handle cycles), time-varying volatilities (conditional variances), time-varying mixing weights with Fréchet Probability Density Function (PDF). Long-memory, heavy-tailed distributed observations are the causal that arise to outliers, change points like behavior, abnormal kurtosis, and skewness. The formulated and proposed  will be an ideal and substitute mixture autoregressive model whenever heavy-tailed distributed observations are the causal that arise to outliers, abnormal kurtosis, and skewness brings about the regime-switching.
will be an ideal and substitute mixture autoregressive model whenever heavy-tailed distributed observations are the causal that arise to outliers, abnormal kurtosis, and skewness brings about the regime-switching. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML