-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2020; 10(4): 97-101
doi:10.5923/j.ajms.20201004.01
Received: Jul. 29, 2020; Accepted: Aug. 22, 2020; Published: Sep. 15, 2020

Sub-Differential Characterizations of Lower Semi-Continuous Quasi-Convex Functions on Infinite-Dimensional Spaces and Optimality Conditions Using Variational Inequalities
Offia A. A.
Department of Mathematics/Computer Science/Statistics/Informatics, Alex Ekwueme Federal University Ndufu-Alike Ikwo (AE-FUNAI), Abakaliki, Ebonyi State, Nigeria
Correspondence to: Offia A. A., Department of Mathematics/Computer Science/Statistics/Informatics, Alex Ekwueme Federal University Ndufu-Alike Ikwo (AE-FUNAI), Abakaliki, Ebonyi State, Nigeria.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

We study optimizations under a weak condition of convexity, called quasi-convexity in infinite dimensional spaces. Although many theorems involving the characterizations of quasi-convex functions and optimizations in finite dimensional spaces appear in the literature, very few results exist on the characterizations of quasi-convex functions in infinite dimensional spaces which involve a generalized derivatives of quasi-convex functions. Although the condition 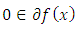 for
for 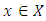 , is known to be necessary optimality condition for existence of a minimizer in quasi-convex programming for some sub-differentials, it is not a sufficient condition. We extend the study of subdifferential characterization of quasi-convex functions in infinite dimensional spaces by using some variational inequalities approach to obtain a necessary and sufficient condition for
, is known to be necessary optimality condition for existence of a minimizer in quasi-convex programming for some sub-differentials, it is not a sufficient condition. We extend the study of subdifferential characterization of quasi-convex functions in infinite dimensional spaces by using some variational inequalities approach to obtain a necessary and sufficient condition for 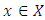 to be either a local minimum or a global minimum.
to be either a local minimum or a global minimum.
Keywords: Quasi-convexity, Quasi-monotonicity, Sub-differential and Variational Inequalities
Cite this paper: Offia A. A., Sub-Differential Characterizations of Lower Semi-Continuous Quasi-Convex Functions on Infinite-Dimensional Spaces and Optimality Conditions Using Variational Inequalities, American Journal of Mathematics and Statistics, Vol. 10 No. 4, 2020, pp. 97-101. doi: 10.5923/j.ajms.20201004.01.
Article Outline
1. Introduction
- The study of Quasi-convex functions and optimizations, which play important roles in numerous fields including, economics, engineering, management science, operations research, industrial organization, computer vision, curve fitting, and various applied sciences, is several decades old. [1,11,19,22]. The notion of Quasi-convex functions and the characteristics convexity of its level set was first recognized by De Finetti in his work, “Sulle Straficazoni Convesse” in 1949, [9]. Since then, efforts have been focused on this class of functions because of its similar features with convex functions and its wider applications [11,14,13,21]. A quasi-convex optimization problem is a mathematical optimization problem in which the objective is to minimize a quasi-convex function over a convex set. Because every convex function is also quasi-convex, Quasi-convex programs therefore generalize convex programs [1].The prefix ‘quasi” means “as if”. Thus, we expect quasi-convex functions to possess some special qualities that are similar to those of convex functions. However, while some properties of convex functions and optimizations have analogues equivalence of quasi-convexity some properties do not have. For instance, although the sub-level sets of both convex and quasi-convex functions are convex, quasi-convex functions differ from convex functions in the following ways among others; quasi-convex functions can be discontinuous in the interior of their domain, not every local minimum is a global minimum, local minimum that are not global cannot be strict minima. First order conditions are not sufficient to identify even local optima under quasi-convexity. [11,14]. Many theorems involving the characterizations of quasi-convex functions and optimizations in finite dimensional spaces appear in the literature. One of the most important properties of convex functions is that their level sets are convex. This property is also a fundamental geometric characterization of quasi-convex functions which sometimes is treated as their definition [10,11,14,19,21]. However, the most attractive characterizations of quasi-convex functions are those which involve gradients (a detailed account of the current state of research on the topic can be found in [5]). As to generalized derivatives of quasi-convex functions, very few results exist (see [5,12]). In [12], a study of quasi-convex functions is presented via Clarke's sub-differential, but the authors restricted themselves to the case of Lipschitz functions on a finite dimensional space only. Interestingly, [21] and independently, [2-4] characterized the lower semi-continuous quasi-convex functions in terms of generalized (Clarke-Rockafellar) sub-differentials and directional derivatives in infinite dimensional spaces with the concept of quasi-monotone maps and prove that a lower semi-continuous function on an infinite dimensional space is quasi-convex if and only if its generalized sub-differential or its directional derivative is quasi-monotone. Although [2-4] and [21] studied the subdifferential characterizations of quasi-convex functions in infinite dimensional spaces, none of the studies covered their optimality conditions in infinite dimensional spaces. [20] did a study on a necessary optimality condition for lower semi-continuous quasi-convex functions on closed convex sets but did not cover the sufficient optimality condition of the problems. He didn’t adopt the variational inequality approach in his study of optimality conditions but rather adopted the normal cone approach in his minimization of the quasi-convex function. Variational inequalities have found many applications in optimization and in order fields of applied, especially in mechanics [15]. Although the condition
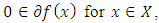 is known to be necessary optimality condition for existence of a minimizer in quasi-convex programming for some sub-differentials, it is not a sufficient condition. We extend the study of [2-4] and [21] by using some variational inequalities approach to obtain a necessary and sufficient condition for
is known to be necessary optimality condition for existence of a minimizer in quasi-convex programming for some sub-differentials, it is not a sufficient condition. We extend the study of [2-4] and [21] by using some variational inequalities approach to obtain a necessary and sufficient condition for 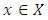 to be either a local minimum or a global minimum.
to be either a local minimum or a global minimum.2. Preliminaries
- Let
 be a Banach space with norm
be a Banach space with norm  its topological dual
its topological dual 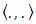 for the duality pairing and
for the duality pairing and 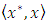 the value of
the value of 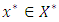 at
at 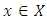 For each
For each 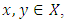 we define the closed line segment
we define the closed line segment 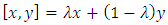 for some for
for some for 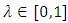 and define
and define 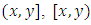 and
and 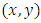 analogously and we denote an open ball centered at
analogously and we denote an open ball centered at 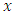 with radius
with radius 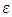 by
by 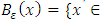
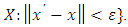 Given a lower semi-continuous (l.s.c.) function
Given a lower semi-continuous (l.s.c.) function 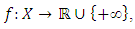 the effective domain is defined by
the effective domain is defined by 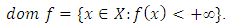 For a multivalued operator
For a multivalued operator 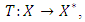 the domain of T is
the domain of T is 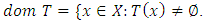 Definition 2.1. A function
Definition 2.1. A function 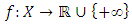 is said to be quasi-convex if for each
is said to be quasi-convex if for each 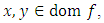
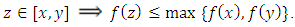 | (1) |
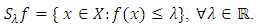 | (2) |
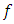 is said to be strictly quasi-convex if the inequality (1) is strict when
is said to be strictly quasi-convex if the inequality (1) is strict when 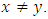 Definition 2.2. [4] A differentiable function
Definition 2.2. [4] A differentiable function 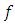 is called quasi-convex if for every
is called quasi-convex if for every 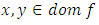
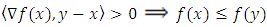 | (3) |
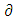 that associates to any l.s.c. function
that associates to any l.s.c. function  and a point
and a point 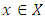 a subset
a subset 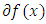 of
of 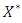 is a sub-differential if it satisfies the following properties:(i)
is a sub-differential if it satisfies the following properties:(i) 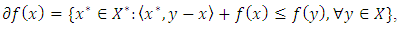 whenever
whenever 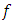 is convex;(ii)
is convex;(ii) 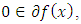 whenever
whenever 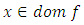 is a local minimum of
is a local minimum of 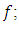 (iii)
(iii) 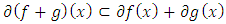 , whenever
, whenever 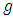 is a real a real-valued convex continuous function which is
is a real a real-valued convex continuous function which is 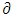 -differentiable at
-differentiable at 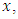 where
where 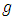 -differentiable at
-differentiable at 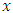 means that both
means that both 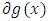 and
and 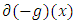 are non-empty. We say that
are non-empty. We say that 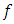 is
is 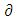 -differentiable at
-differentiable at 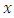 when
when 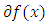 is non-empty while
is non-empty while 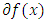 are called the sub-gradients of
are called the sub-gradients of 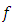 at
at 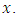 The Clarke-Rockafellar general derivative of
The Clarke-Rockafellar general derivative of 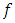 at
at 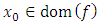 in the direction
in the direction 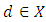 is given by
is given by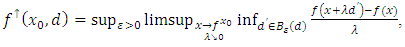 where
where 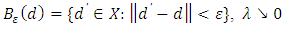 indicates the fact that
indicates the fact that 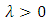 and
and 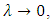 and
and 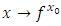 means that both
means that both 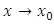 and
and 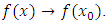 The Clarke-Rockafellar subdifferential of
The Clarke-Rockafellar subdifferential of 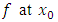 is defined by
is defined by 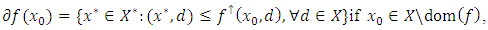 then
then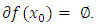 We extend the notion of quasi-convexity to less smooth function using the concept of generalized directional derivatives and sub-differential.Definition 2.4. [4] A l.s.c function
We extend the notion of quasi-convexity to less smooth function using the concept of generalized directional derivatives and sub-differential.Definition 2.4. [4] A l.s.c function 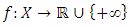 is called quasi-convex (with respect to Clarke-Rockerfeller Subdifferentials) if for any
is called quasi-convex (with respect to Clarke-Rockerfeller Subdifferentials) if for any 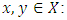
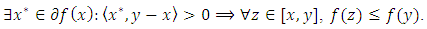 | (4) |
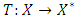 is said to be quasi-monotone if
is said to be quasi-monotone if 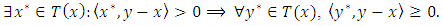
3. Sub-Differential Characterizations of Quasi-Convex Functions
- Our aim is to show that
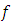 if quasi-convex if and only
if quasi-convex if and only 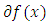 is quasi-monotone. We need the following lemma.Lemma 3.1. Let
is quasi-monotone. We need the following lemma.Lemma 3.1. Let 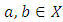 with
with 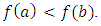 Then, exist
Then, exist 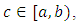 and sequence
and sequence 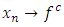 and
and 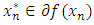 with
with 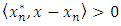 for every
for every 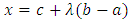 with
with 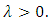 Proof. By Approximate mean value inequality theorem [3], we can find an
Proof. By Approximate mean value inequality theorem [3], we can find an 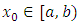 and a sequence
and a sequence 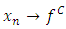 and
and 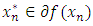 verifying
verifying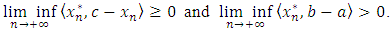 | (5) |
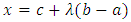 with
with 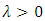 it holds
it holds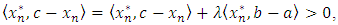 | (6) |
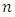 sufficiently large.Theorem 3.2. (Quasi-convexity).
sufficiently large.Theorem 3.2. (Quasi-convexity). 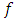 is quasi-convex if and only if
is quasi-convex if and only if 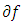 is quasi-monotone.Proof. We show that if
is quasi-monotone.Proof. We show that if 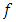 is not quasi-convex then,
is not quasi-convex then, 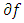 is not quasi-monotone. Suppose that there exist some
is not quasi-monotone. Suppose that there exist some 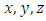 in
in 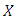 with
with 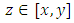 and
and 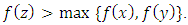 According Lemma 3.1 applied with
According Lemma 3.1 applied with 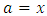 and
and 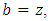 there exists a sequence
there exists a sequence 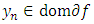 and
and 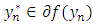 such that
such that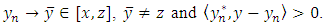 | (7) |
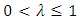 be such that
be such that 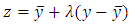 and set
and set 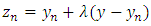 , so that
, so that 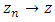 . Since
. Since 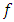 is lower semi-continuous, we may pick
is lower semi-continuous, we may pick 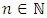 very large with
very large with 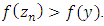 Apply Lemma 3.1 again with
Apply Lemma 3.1 again with 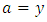 and
and 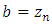 to find sequences
to find sequences 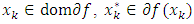 such that
such that 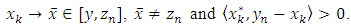 | (8) |
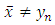 and
and 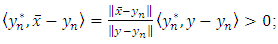 | (9) |
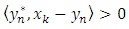 for
for 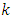 sufficiently large. But
sufficiently large. But 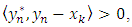 showing that
showing that 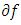 is not quasi-monotone. Conversely, we suppose that
is not quasi-monotone. Conversely, we suppose that 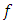 is quasi-convex and show that
is quasi-convex and show that 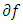 is quasi-monotone. Let
is quasi-monotone. Let 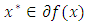 and
and 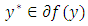 with
with 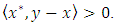 We need to verify that
We need to verify that 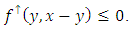 We fix
We fix 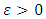 and
and 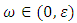 such that
such that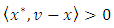 for all
for all 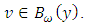 We fix
We fix 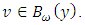 Since
Since 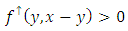 we can find
we can find 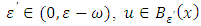 and
and 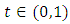 such that
such that 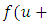
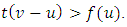 From the quasi-convexity of
From the quasi-convexity of 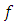 we deduce that
we deduce that 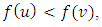 whence,
whence,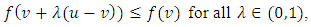 so that
so that 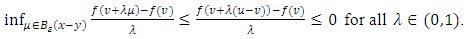 Combining the inequalities and for any
Combining the inequalities and for any 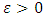 there exists
there exists 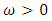 such that
such that 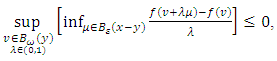 which shows that
which shows that 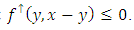
4. Optimality Conditions and Variational Inequalities
- Let
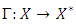 be a multivalued operator,
be a multivalued operator, 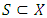 and
and 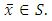 Recall from [17,18] that,
Recall from [17,18] that, 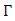 satisfies the variational inequality (10) if and only if
satisfies the variational inequality (10) if and only if 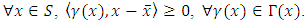 | (10) |
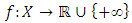 be a lower semi-continuous (l.s.c.) function and consider the minimization problem
be a lower semi-continuous (l.s.c.) function and consider the minimization problem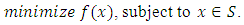 | (11) |
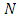 is a convex open neighborhood of
is a convex open neighborhood of 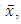 we have the followingLemma 4.1. If
we have the followingLemma 4.1. If 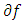 satisfies (10), the following assertions hold.(i) If
satisfies (10), the following assertions hold.(i) If 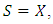 then
then 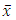 is a global minimum of
is a global minimum of 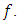 (ii) If
(ii) If 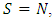 then
then 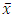 is a local minimum of
is a local minimum of 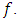 Proof. It suffices to prove (ii) Suppose by contradiction that
Proof. It suffices to prove (ii) Suppose by contradiction that 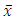 is not a solution of (11), then there exist
is not a solution of (11), then there exist 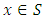 such that
such that 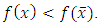 By Lemma 3.1, there exist
By Lemma 3.1, there exist 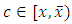 and two sequences
and two sequences 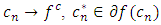 with
with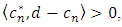 for any
for any 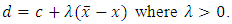 Since
Since 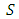 is a convex open neighborhood of
is a convex open neighborhood of 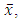 then
then 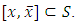 Furthermore, for
Furthermore, for 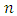 large enough
large enough 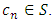 For
For 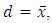 we have
we have 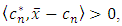 which contradicts (10). Thus,
which contradicts (10). Thus, 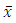 is a local minimum of
is a local minimum of 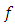 .Consider now the quasi-convex minimization problem (11) again,
.Consider now the quasi-convex minimization problem (11) again, 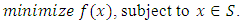 | (12) |
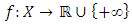 is l.s.c. and quasi-convex, then we have:Theorem 4.2. If
is l.s.c. and quasi-convex, then we have:Theorem 4.2. If 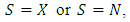 then the following assertions are equivalent:(i)
then the following assertions are equivalent:(i) 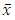 is an optimal solution of (12).(ii)
is an optimal solution of (12).(ii) 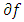 satisfies (10).Proof.
satisfies (10).Proof.  Suppose
Suppose  is a strict minimum of (12). Then for all
is a strict minimum of (12). Then for all 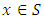 such that
such that 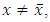 we have
we have 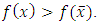 By Lemma 3.1, there exist
By Lemma 3.1, there exist 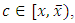 and two sequences
and two sequences 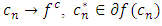 with
with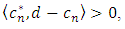 for any
for any 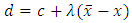 where
where 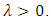 For
For 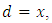 we have
we have 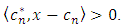 Since
Since 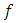 is quasi-convex, by Theorem 3.2.,
is quasi-convex, by Theorem 3.2., 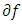 is quasi-monotone. This implies that
is quasi-monotone. This implies that 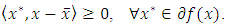 Thus,
Thus, 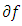 satisfies the variational inequality (10)Suppose that
satisfies the variational inequality (10)Suppose that 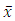 is not is a strict minimum of (12) and consider the function
is not is a strict minimum of (12) and consider the function 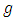 defined by
defined by 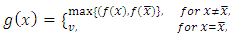 | (13) |
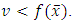 it is obvious that
it is obvious that 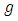 is l.s.c., quasi-convex and
is l.s.c., quasi-convex and 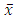 is a strict local minimum of
is a strict local minimum of 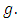 Then, we have
Then, we have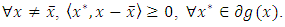 Since
Since 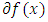 depends only on the values of
depends only on the values of 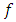 in the neighborhood of
in the neighborhood of 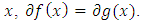 When
When 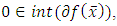 i.e. the interior of
i.e. the interior of 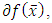 we obtain a more precise resultLemma 4.3. If
we obtain a more precise resultLemma 4.3. If 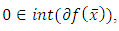 then
then 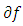 satisfies the variational inequality (10) on the whole space
satisfies the variational inequality (10) on the whole space 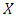 and
and 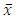 is an optimal solution of (12) with
is an optimal solution of (12) with 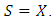 Moreover,
Moreover, 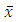 is a global minimum of
is a global minimum of 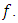 Proof. Suppose that
Proof. Suppose that 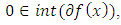 then
then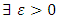 such that
such that 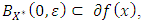 where
where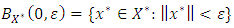 Let
Let 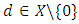 and consider the linear mapping
and consider the linear mapping 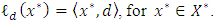 By open mapping theorem [4, Pseudo 8], we
By open mapping theorem [4, Pseudo 8], we 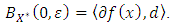 Since
Since 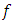 is quasi-convex, then
is quasi-convex, then 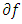 is quasi-monotone. By Definition 2.1 of [16], the multivalued operator
is quasi-monotone. By Definition 2.1 of [16], the multivalued operator 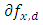 defined by
defined by 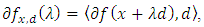 is quasi-monotone. And then,
is quasi-monotone. And then,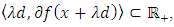 for all
for all 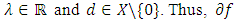 satisfies (10).
satisfies (10).5. Conclusions
- We have studied optimizations under a weak condition of convexity, called quasi-convexity in infinite dimensional spaces. Although many theorems involving the characterizations of quasi-convex functions and optimizations in finite dimensional spaces appear in the literature, very few results exist on the characterizations of quasi-convex functions in infinite dimensional spaces which involve a generalized derivatives of quasi-convex functions. Although the condition
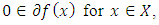 is known to be necessary optimality condition for existence of a minimizer in quasi-convex programming for some sub-differentials, it is not a sufficient condition. This study is an extension of the study of [2-4] and [21] by using some variational inequalities approach instead of the normal cone approach to obtain a necessary and sufficient condition for
is known to be necessary optimality condition for existence of a minimizer in quasi-convex programming for some sub-differentials, it is not a sufficient condition. This study is an extension of the study of [2-4] and [21] by using some variational inequalities approach instead of the normal cone approach to obtain a necessary and sufficient condition for 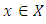 to be either a local minimum or a global minimum.
to be either a local minimum or a global minimum.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML IOSR Journal of Mathematics (IOSR-JM), Volume 10, Issue 4 Ver. III (2014) PP 44-53.
IOSR Journal of Mathematics (IOSR-JM), Volume 10, Issue 4 Ver. III (2014) PP 44-53.