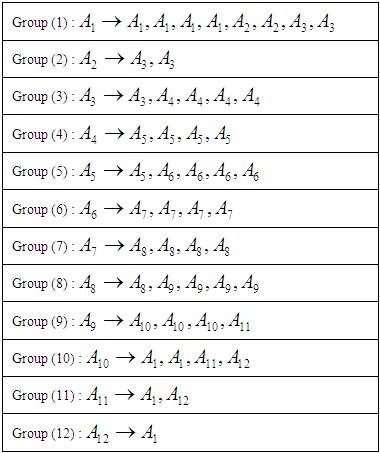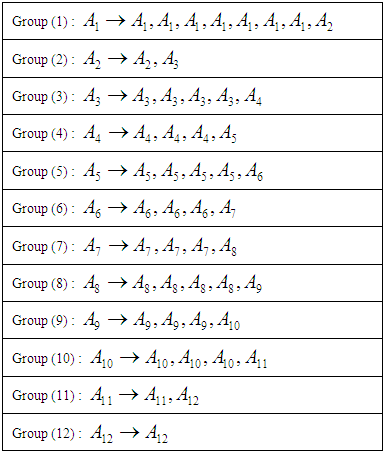-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2020; 10(3): 79-95
doi:10.5923/j.ajms.20201003.03
Received: Aug. 10, 2020; Accepted: Aug. 25, 2020; Published: Sep. 5, 2020

Methods in Fuzzy Time Series Prediction with Applications in Production and Consumption Electric
Mohammed Eid Awad Alqatqat, Ma Tie Feng
Department of Statistics, Southwestern University of Finance and Economics, Chengdu, China
Correspondence to: Mohammed Eid Awad Alqatqat, Department of Statistics, Southwestern University of Finance and Economics, Chengdu, China.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, we focus on improving the accuracy of Fuzzy time series forecasting methods. We used a FCM method to construct a fuzzy clustering. we suggest a new method for forecasting based on it, The new method integrates the fuzzy clustering with FTS to reduce subjectivity and improve its accuracy, FTS attracted researchers because of its ability to predict the future values in some issues. the new method for forecasting based on re-established a fuzzy group relation based on its membership degrees to each cluster, and using these memberships to defuzzify the results. A case study of production and consumption electric shows that the suggested method is feasible and efficient. The accuracy of three methods is verified by using the Mean Absolute Deviation (MAD), Mean Absolute Percentage Error (MAPE); the result shows that the Suggested Method has smaller MAPE, MAD, from Chen method and Fuzzy Time Series c-means.
Keywords: Fuzzy cluster, Fuzzy c-means method, Fuzzy time series, Clustering
Cite this paper: Mohammed Eid Awad Alqatqat, Ma Tie Feng, Methods in Fuzzy Time Series Prediction with Applications in Production and Consumption Electric, American Journal of Mathematics and Statistics, Vol. 10 No. 3, 2020, pp. 79-95. doi: 10.5923/j.ajms.20201003.03.
Article Outline
1. Introduction
- Forecasting production and its consumption electric elements are a major area that utilizes different models and future forecasting. Different models are used for getting prediction about the pattern of future behavior. A satisfactory degree of statistical validity obtains through every energy series according to optimum forecasting models. And also establish regional energetic planning according to their requirement. There are two main models utilize in the forecasting production and consumption electric according to nature of requirement. These models involve Fuzzy time series and Fuzzy C-Means. Fizzy time series and Fuzzy C means have their abilities and according to their nature of performance, they both handle a different kind of data according to their utilization [1].The concept of the fuzzy group and the fuzzy logic, which was proposed by the Azerbaijani scientist of origin, Lotfi Zadeh in 1965, was subsequently applied in a wide and varied manner to different systems, especially the complex Ones, as the increase in complexity in the systems increases the uncertainty and thus leads to a lack of information and the term uncertainty emerged, To reinforce the position of probability theory.The theory of probability and the theory of fuzzy groups facilitate two types of uncertainty, which generally come as a result of two reasons, the first of which is the method of measurement to reach new knowledge and the second is the natural language for communicating with others in order to deal with the problems of uncertainty. The probability theory can be successfully applied to large areas of science because it is concerned with treating the occurrence of Random future incidents based on currently available information. Despite the success of probability theory, it is still unable to show uncertainty with high accuracy, and it is also unable to show uncertainty in the results either. Controlling the linguistic terms expressing natural characteristics such as length, temperature, etc. have contributed to the emergence and development of the Concept of the fuzzy group.Cluster analysis is one of the methods used statistically to classify data primarily into a set of nodes (clusters). Each cluster contains a set of data that have common structural characteristics and this is preferred by most methods of distinguishing patterns because the data will be distributed over a number of clusters so that each cluster contains Elements have similar characteristics among themselves, which requires that there be separate clusters from each other, so that each pattern belongs to one cluster and only one in the case that the clusters represent regular groups. As for the fact that the clusters may represent fuzzy groups, the cloudy cluster makes the concept of fragmentation wider in a way that allows any pattern to have a relationship of belonging to any of the clusters using a membership function that ranges between zero and one so that the value of the membership function of any type indicates higher Reliability for belonging of this pattern to a particular cluster. The output of the fuzzy cluster algorithms is called fuzzy segmentation. These algorithms and methods occupy a wide area in research and studies and in all fields. The most famous techniques of the fuzzy cluster are the fuzzy-c-medium algorithm or method, abbreviated as FCM, which was proposed by Besdek more than 25 years ago. As for the fuzzy time series, it was proposed in 1993 by the two scientists chissom and song and they developed two definitions of the fuzzy time series models that are not time variable and time variable and which are used in the forecasting. The time series is defined in terms of relationships, and the final step involves raising the fuzziness defuzzification of the predictive results. Most Studies and research in the field of fuzzy time series are concerned with the methods of forming the fuzzy group and the fuzzy relationships. There are fuzzy time series from the first order and higher ranks depending on the logical relationships between the fuzzy groups and research trends in this field include methods of forming fuzzy groups, the most famous of which is the method and research directions are divided into Several trends regarding the effect of the number of fuzzy groups, the order of the fuzzy time series, and the defuzzification methods on the accuracy of the prognostic results.
2. Summary of Literature Review
- Fizzy Time Series is an algorithm, which, is used in the processing of huge data. It is a model used for programming for data processing in different languages including Java, Ruby, Python, and C++ as well. By using multiple machines in the cluster, large-Scale data can be analyzed by using parallel nature Map Reduce programs in nature. There are four stages from passing these, Map Reduce can only work properly and can provide efficient and excellent results successfully. These four phases are mapping, splitting, reducing and shuffling [2]. A chunk of input that by the consumption through a single map is divided into fixed-size pieces to process is efficiently and hence these Input slits make the processing quick and easy. In the time series program, the first step is the Mapping. To produce output values, the data from each slip to a mapping function passed in this phase [3]. The mapping phase output is consuming in this phase as it is going to consolidate the output from the mapping phase into relevant records. Along with their respective frequency, the same words are clubby together. The output values are aggregate from the shuffling phase. A single output value comes in return for this phase after shuffling [4]. The complete data set is summarizing in this phase [5]. Usually at the reliability level of data Centre and usually at scale Cloud computing is designed to provide on-demand resources and services to programs on the internet. Along with Map Reduce cloud computing works and this increases the efficiency of working of both the programs in programming or processing of data [6] [7]. As discussed above, Map Reduce helps to process data through its programming model that is specially designed to process a large amount of data efficiently after dividing that large amount into small chunks. There are some capacity-on-demand styles of clouds that support the parallel programming of Map Reduce which are Google's Big Table, Hadoop and sector [8].Accuracy in the forecasted value is the major problem in the fuzzy time series forecasting. New techniques for fuzzy time series forecasting also introduce that used different parameters to generate better results. For forecasting, a different approach also utilizes that is known as a simplified computational approach according to proposed methods [9].In a particular domain, the time series is an orderly sequence of values of different variables. In the area of time series analysis, challenging tasks are part of forecasting techniques. In the area of tourism, agriculture, employment, climatology and economy forecasting show significant impact on the decision making area. From natural calamities, timely forecast help to save from any loss. As an emergent research area, fuzzy tie series forecasting is acted in this regard. It handles a different kind of problems according to imprecision, vagueness ad uncertainty [10].Forecasting methods and time series analysis are very commonly used in different areas like meteorology, economy, medicine and engineering according to the nature of work [11]. From the traditional and consecrated statistical tools to the new computational intelligence tools according to several methods of analysis and forecasting, fuzzy time series is most effective methods and it provides many attractive features to its users like scalability, simplicity, manageability and readability [12].The asset is defining as a dichotomy where every element involves in the set according to logical theory and classical mathematics. It imposes inflexible and strong boundaries according to a valuable set of data. Because innumerable realities are not so effective for the human being so this dichotomous way of thinking is not convenient. The logic of Fuzzy imposes the duality instead of dichotomy that may belong to different set to a certain level and sometimes belong with each other with the strong member’s ship of each value [13], [14].Time series is a combination of different data according to the behavior of random variable overtime and their analysis must take into account the order in that were collected and successive record of this variable are not independent of each other. According to Ehlers, it is interested in analyzing and modeling this dependence and the neighboring observation are dependent, which show that past or lagged value of the same series are used for predicting future values of time series. Autoregressive model is considered a simple example where P show lagged variable utilize in the forecasting model [15].The idea of time series s divides into fuzzy sets and study in-depth about behaves in every area. As value jump one place to another, how the partitions related to themself over time according to rules of this model. The fuzzy time series methodology can be distributed into two procedures one is training and the next one is forecasting [16], [17].Training procedures involve some basic steps to consider the utilization of this procedure according to fuzzy time series which include Definition of the Universe of Discourse U, create the Linguistic Variable A, Fuzzyfication, creating the temporal pattern, creating rules and with these steps, there are also many benefits of this procedure like it is easy to update and attractive for mostly changing data and it is easy to parallelize that has also become attractive for the major data [18].Forecasting procedures help to determine the future data according to prediction and utilize this procedure after proper training to handle the data. This procedure involves many steps like input value fizzy fiction; find the compatible rules and De-fuzzy fiction [19]. These two procedures help the fuzzy time series forecasting according to data and its nature of utilization [20].It is also a contested concept because of 'ambiguity' over the concept and definition of security. Every other scholar has defined security following what they feel the security to be. Some various factors and variables are needed to be addressed if we aim at achieving 'maximum security' in a state [21]. Also, we have to define and realize what security is for. At what risk and at what cost we are seeking. What can be the possible road map to achieving security? As stated above security is a contested concept with everyone having their version of security? A complete algorithm is developing by using the historical data and utilizes them for forecasting process according to this proposed model [22].Now with the fuzzy time series forecasting model, we are also discussing the Fuzzy C-Means model for the forecasting production and consumption of electricity. Fuzzy C-Means algorithm is utilizing the incorporated spatial information for clustering according to member functions. For economic prosperity, there should be a well-planned and efficient transport network because they can affect the society and natural environment and could play an important role in transforming communities with proper planning and strategy. Safety is a critical aspect of the Electric consumption system and it must be catering while planning and strategizing Electric consumption system. Safety is not limited to any person or living thing, it caters the environmental safety, land safety and safety for the societies [23], [24], [25].To tackle the Electric consumption issues or planning for new Electric consumption facilities than it should containA feasibility report, of whether it will be facilitating the economy or not. The feasibility report tells us how long this system or policy can go and what benefits could be taken. There should be enough planning of moving long vehicles with short vehicles and plans to tackle traffic jams in rush hours. This is an important part of planning to keep in mind about the movement of goods containing vehicles. Planning of Electric consumption and land goes side by side to accommodate the effects of land use on Electric consumption demand and supply and the effects of Electric consumption on land. There must be provided ways through which achievement of social goals will be attainable through Electric consumption systems. Identification of those strategies is important which provides access to persons with disabilities and improves public health and safety with the help of improving air quality and reducing road collision [26].This research is written by Mahadevan, Sharma and Banerjee in which they have discussed the energy importance within the framework of network devices. For the enterprises and data Centre networks, energy efficiency is becoming increasingly important for operating networking infrastructure. The researchers have proposed many strategies to manage the power consumption of network devices. The strategies emphasize on the usage of a variety of switches and routers which will be useful to save the power of various network devices [27] [28]. In this paper, authors have discussed the hurdles in network power instrumentation but they have also provided the study of power measurements such as varieties of networking gears which includes wireless access points, routers, core switches, and edge switches [29].They have built a benchmark through which users will be able to measure the power consumed by each device and also could be able to compare the power of each device [30]. In today's world, energy efficiency is the main point or agenda of every company and firm without which the company could not be able to reduce their costs. Now a day's only energy-efficient companies should survive for years. A study shows that the US is consuming 6.06 Terra Watt Hours through networking devices yearly [18].In the case of large data, VL data options are used according to large data requirement in the management of data sets. In different applications, data mining communities to search VL databases and clustering is one of the basic tasks used in pattern making and its recognition. Algorithm of clustering is considering very important to well scale the very large data and effectively used in many dimensions. To extend fuzzy C-Means clustering to very large data, three different efficacies according to implementation techniques are used according to the need of data [31]. Next, the incremental techniques that make one sequential pass through subsets of the data and the last one are sampling followed by no iterative extensions [32].In the end, they make experiments which include shutdown overhead and energy consumption. They stated that power management is the mainstream of embedded systems and lays down different important aspects for these systems. The power management can lead the embedded systems to longer battery life as well as it will provide static power consumption. The consumption of power is reduced due to the switching of energy [33]. They said that the development of dynamic voltage scaling is designed to minimize dynamic power consumption which is a dominant factor. Due to the time and energy cost associated with shutdown, longer shutdown intervals are better [34].When clustering the unlabeled data, fuzzy possibilities C-Means and algorithm also generate membership and typically values. The sum over all data points of typicality to a cluster is one when the FPCM constrains the typicality values according to requirements. For large data sets, the row sum constraints produce unrealistic typicality values as par nature of the information. a new kind of model utilizes in this regard which is known as possibility fuzzy C-Mean model. With the usual point prototype or cluster centers of each cluster, PFCM produces membership and possibilities al the same time according to the requirement of data [35].They have discussed the importance of power, and what are the characteristics of the power model. They also critically examine the speed of power and make real-time scheduling. Their real-time scheduling includes DVS and critical speed, shutdown overhead, and computation has been done through algorithms. The concept of security has long been a neglected and limited concept for the world [36] [37]. In reality, the security is vast and a very important concept that is for the reason that countries take extreme measures over the context of security itself. As stated above security in past was only associated with the use of hard military power but in contemporary times, the concept of security has changed [38]. The different comparison also presents between FCM and PCM with the PFCM according to different data sets. It also explains that both types of comparisons are favorable for the models and generates better outcomes. The following piece of writing is an attempt to re-define the core concept of security. Every time the word 'security' comes up, it is treated or is usually associated with 'Hard military power'. While there are many with various proposals considering issues like poverty, drug trafficking. Economic is part of security. It is very important to identify various aspects of security because with time the concept of security changes [39].
3. Basic Concepts Fuzzy Sets and Their Properties & Crisp Set
3.1. Set Crisp
- A set crisp is defined as a collection of elements and objects
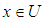 That is the element x belongs or does not belong to the group A and
That is the element x belongs or does not belong to the group A and 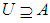 , Where
, Where 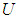 is the overall group and when it is said that
is the overall group and when it is said that 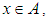 this statement is either true or false and that all elements of the universal group U can be determined to be either members or not members of group A, which we can know Function characteristic [40].This function of group A is symbolized by the symbol
this statement is either true or false and that all elements of the universal group U can be determined to be either members or not members of group A, which we can know Function characteristic [40].This function of group A is symbolized by the symbol 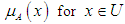 , and its formula is as follows:
, and its formula is as follows: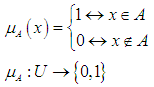 | (3.1) |
3.2. Fuzzy Set
- Let group A be within the universal group U, since each element in U can be an element in A, but the degree of its membership is determined by a real value within the period [0,1] and that the membership function of group A is defined as follows:
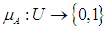 There are an unlimited number of organic functions, the most famous of which are the trigonometric, trapezoid, and bell-shaped function. Through this expression, it is possible to obtain complete information about the degree of membership of any element in A within the universal group U if
There are an unlimited number of organic functions, the most famous of which are the trigonometric, trapezoid, and bell-shaped function. Through this expression, it is possible to obtain complete information about the degree of membership of any element in A within the universal group U if 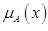 represents the degree of membership for element x within the group A and the fuzzy group A is expressed by ordered pairs for each element and its membership function, as follows:
represents the degree of membership for element x within the group A and the fuzzy group A is expressed by ordered pairs for each element and its membership function, as follows: 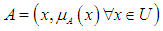 | (3.2) |
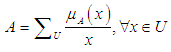 | (3.3) |
3.3. Linguistic Variables
- Fuzzy numbers are often used to represent quantitative variables, and they are called theseNumbers in the name of linguistic variables, linguistic variables are an expression of words or sentences in the form of numerical values, all values taken from a group of expressions (terms) that contain a set of acceptable values and its elements are in the form (value / concept). And each (value / concept) in the expression group is expressed in a fuzzy number and is known to the global period or part of it is called the base variable, and in short, this relationship is expressed as
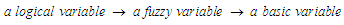
3.4 Fuzzification
- It is the process of converting assertive fragile values into fuzzy ones, using the organic functions of fragile values that take different shapes, including trigonometric, semi-trapezoid, and natural... etc. and whose membership values are limited between zero and one. There are different ways to do this that can be carried out through intuition, genetic algorithms, or neural networks.
3.5. Defuzzification
- It is the process of converting fuzzy outputs into fuzzy outputs that take real numerical values and this is done in several different ways and is done in several ways by raising the Defuzzification, including:a. Max-membership principleIn this rule, the value of Z after raising the Defuzzification is equal to the value of x with the highest organic degree, expressed as:
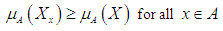 | (3.4) |
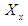 is the value that has the highest degree of membership in the fuzzfied group A, and if we take the following example for group A = 0.3 / 10 + 0.45 / 12 + 0.6 / 15 + 0.9 / 17 then Z = Max (A) = 17.b. Centroid MethodThis method is widely used, and it is also called the center of gravity method or the area center method, and in the case of the membership function
is the value that has the highest degree of membership in the fuzzfied group A, and if we take the following example for group A = 0.3 / 10 + 0.45 / 12 + 0.6 / 15 + 0.9 / 17 then Z = Max (A) = 17.b. Centroid MethodThis method is widely used, and it is also called the center of gravity method or the area center method, and in the case of the membership function 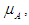 it is known as discrete
it is known as discrete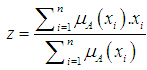 | (3.5) |
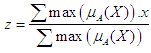 | (3.6) |
3.6. Some Definition Related To Fuzzy Time Series
- Fuzzy time series was first defined by the two scientists Song and Chissom in the year 1993, and the concept of fuzzy time series can be described in the following terms:Suppose U is a crowd of things representing the universal space ending where
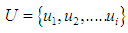 the fuzzy group
the fuzzy group 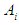 can be defined with respect to U by the equation
can be defined with respect to U by the equation 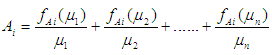 | (3.7) |
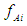 a membership function is fuzzy set
a membership function is fuzzy set 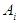 so
so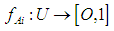 | (3.8) |
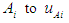 is the degree that is owned by
is the degree that is owned by 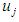 against
against 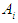 .
.3.6.1. First Definition: Fuzzy Time Series
- Let Y (t) (t =..., 0,1,2,...) subset
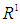 , become a universe discourse with the fuzzy set
, become a universe discourse with the fuzzy set 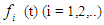 defined and F (t) is a collection of
defined and F (t) is a collection of 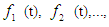 then F (t) is called fuzzy time series defined in Y (t) (t =..., 0,1,2,...). From this definition F (t) can be understood as a linguistic variable
then F (t) is called fuzzy time series defined in Y (t) (t =..., 0,1,2,...). From this definition F (t) can be understood as a linguistic variable 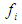
 of the linguistic probability value F (t) [41]. Because at different times, the value of F (t) can be different, F (t) as a fuzzy set is a function.From time t and universe discourse is different at each time so Y (t) is used for time t (Song and Chissom, 1993).
of the linguistic probability value F (t) [41]. Because at different times, the value of F (t) can be different, F (t) as a fuzzy set is a function.From time t and universe discourse is different at each time so Y (t) is used for time t (Song and Chissom, 1993).3.6.2. Second Definition: Fuzzy Relationship
- Suppose F (t) is caused only by F (t-1) and appointed with
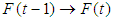 then there is Fuzzy Relations between F(t) and F(t-1) expressed by the formula
then there is Fuzzy Relations between F(t) and F(t-1) expressed by the formula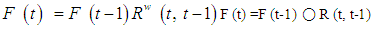 Where
Where 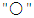 is the Max-Min composition operator. The relation R is called the first order model F (t).Furthermore, if the fuzzy relation
is the Max-Min composition operator. The relation R is called the first order model F (t).Furthermore, if the fuzzy relation 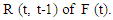 t is time independent so for different times
t is time independent so for different times 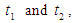
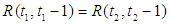 So that F (t) called time-invariant fuzzy time series.
So that F (t) called time-invariant fuzzy time series.3.6.3. Third Definition: Invariant Fuzzy Time Series Time
- Suppose F (t) is caused only by F(t-1) and appointed with then there is Fuzzy Relations between F(t) and F(t-1) expressed by the formula
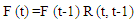 | (3.9) |
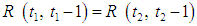 So for different times
So for different times 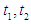 so that F (t) called time-invariant fuzzy time series and the opposite of this called time-variant fuzzy time series [42].
so that F (t) called time-invariant fuzzy time series and the opposite of this called time-variant fuzzy time series [42]. 3.6.4. Fourth Definition: N-Order Fuzzy Relation
- If F (t) is produced by several fuzzy setsF (t – n), F (t - n +1)... F (t -1)Then the fuzzy relationship is symbolized by:
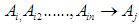 Where
Where 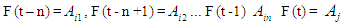 And such relationships are called
And such relationships are called 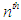 order fuzzy time series.The concept of the nth time series was proposed by Chen in 2002 and used to predict the number of students admitted to the University of Alabama.
order fuzzy time series.The concept of the nth time series was proposed by Chen in 2002 and used to predict the number of students admitted to the University of Alabama.3.6.5. Fifth Definition: Fuzzy Logic Relationship Group
- Relationships on the same fuzzy group on the left end can be grouped into a group of relationships, let's assume that they are fuzzy logical relationships in the form [42]:
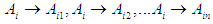 | (3.10) |
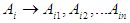 And no fuzzy group can appear at the right end more than once. The term relationship group first appeared from scientist Chen in 1996.
And no fuzzy group can appear at the right end more than once. The term relationship group first appeared from scientist Chen in 1996.4. Methods
4.1. Chen Method Review
- This method is a simple model proposal that includes simple mathematical operations. The suggested step-by-step procedure can be described as the following steps:1- Dividing the discourse of Universe into periods of equal length2- Defining the fuzzy groups on the global event.3- Fuzzify historical data.4- Identify fuzzy relationships.5- Establish groups or groups of fuzzy relationships.6- Defuzzify the forecasted output.The steps involved in the Chen methodStep one: The first step: Define the global event and divide it into periods of equal length. The global event U is defined
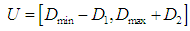 Where
Where 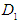 and
and 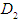 are the corresponding positive numbers, they are chosen to complement the minimum and maximum values to be indivisible values, which facilitate their calculation.Where
are the corresponding positive numbers, they are chosen to complement the minimum and maximum values to be indivisible values, which facilitate their calculation.Where 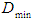 and
and 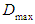 , they are the lowest and highest data values, respectively. The global event is divided into several periods. For example, if the number of periods is 7,
, they are the lowest and highest data values, respectively. The global event is divided into several periods. For example, if the number of periods is 7, 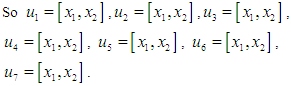 The second step: Defining the fuzzy groups on the global event. Suppose that
The second step: Defining the fuzzy groups on the global event. Suppose that 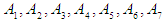 is the fuzzy groups as they are linguistic values of the linguistic variables of the data under study. Fuzzy groups
is the fuzzy groups as they are linguistic values of the linguistic variables of the data under study. Fuzzy groups 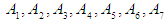 identify the global event as
identify the global event as 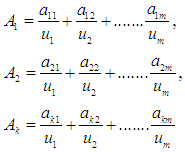 Whereas
Whereas 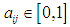 and
and 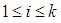 and
and 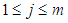 And
And 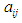 represents the degree of membership for the assertive period
represents the degree of membership for the assertive period 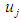 in the
in the 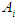 fuzzy group.Before defining the fuzzy groups as U, the syntactic values must be assigned to each fuzzy group.Fuzzy groups can define a wild event as follows:
fuzzy group.Before defining the fuzzy groups as U, the syntactic values must be assigned to each fuzzy group.Fuzzy groups can define a wild event as follows: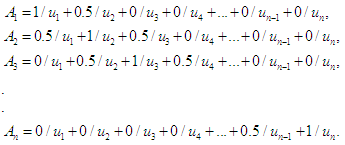 In general, the expression can be written as [43]
In general, the expression can be written as [43]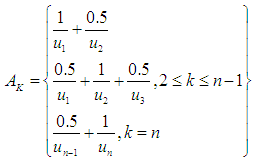 | (4.1) |
 , then F (t-1) Fuzzify the set
, then F (t-1) Fuzzify the set  . Let us take the example that we wanted to fluctuate the value at the year (1970), so we calculate the highest degree of belonging to the value in any period, let it be
. Let us take the example that we wanted to fluctuate the value at the year (1970), so we calculate the highest degree of belonging to the value in any period, let it be  , so F (1970) is in group
, so F (1970) is in group 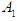 , but the value at year (1971) has the highest degree of affiliation in the period
, but the value at year (1971) has the highest degree of affiliation in the period 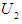 , so F (1971) fog to set
, so F (1971) fog to set 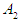 and so on for all data.Step 4: Distinguish Fuzzy Relationships In this step; relationships are distinguished from fuzzing historical data. If the time series variable F (t-1) is fuzzed in the fuzzy set
and so on for all data.Step 4: Distinguish Fuzzy Relationships In this step; relationships are distinguished from fuzzing historical data. If the time series variable F (t-1) is fuzzed in the fuzzy set 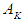 and F (t) in
and F (t) in 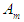 then
then 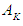 is related to
is related to 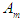 . And we symbolize this relationship in the form
. And we symbolize this relationship in the form 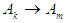 , where
, where 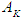 in the current case and
in the current case and 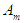 is the subsequent case of the statement value for a particular year, and from the example in the previous step we can say that the relationship between (1970) and (1971) is
is the subsequent case of the statement value for a particular year, and from the example in the previous step we can say that the relationship between (1970) and (1971) is 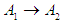 and
and 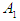 is called the left hand side, and
is called the left hand side, and 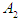 right hand side, and so on for all data, Note that it is not possible for repeated relationships of the same type only once and ignore the rest.The fifth step: This step can be summarized as establishing fuzzy relationship groups. If the fuzzy group has a fuzzy relationship with more than one group, then the groups on the right side are merged or grouped more than once. This is called establishing fuzzy relationship groups. As an illustrative example, the establishment of relationship groups is in our paper Scientific is as
right hand side, and so on for all data, Note that it is not possible for repeated relationships of the same type only once and ignore the rest.The fifth step: This step can be summarized as establishing fuzzy relationship groups. If the fuzzy group has a fuzzy relationship with more than one group, then the groups on the right side are merged or grouped more than once. This is called establishing fuzzy relationship groups. As an illustrative example, the establishment of relationship groups is in our paper Scientific is as 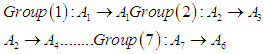 Step 6: Raise the fuzziness to calculate the predictive results and assuming that the fuzziness is for the value of the indication from F (t-1) it is
Step 6: Raise the fuzziness to calculate the predictive results and assuming that the fuzziness is for the value of the indication from F (t-1) it is  The results of the prediction of F (t) are determined according to the following principles:1- If there is a one-to-one relationship (1-1) in the relations group for
The results of the prediction of F (t) are determined according to the following principles:1- If there is a one-to-one relationship (1-1) in the relations group for  , say
, say 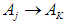 , and the highest degree of affiliation with
, and the highest degree of affiliation with 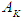 is in the period
is in the period 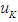 , then the results of the prediction for F (t) are equal to the midpoint of the period
, then the results of the prediction for F (t) are equal to the midpoint of the period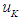 .2- If
.2- If 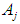 is not related to any other group, i.e.
is not related to any other group, i.e. 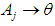 where
where 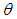 is the empty group, and the highest degree of affiliation with
is the empty group, and the highest degree of affiliation with 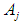 is in the period
is in the period 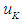 , then the results of the prediction are equal to the middle of the period
, then the results of the prediction are equal to the middle of the period 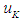 .If there are one-to-many relationships in groups of fuzzy relationships of
.If there are one-to-many relationships in groups of fuzzy relationships of 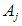 , let's say
, let's say 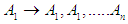 , and that the highest degree of affiliation occurs in interval
, and that the highest degree of affiliation occurs in interval 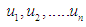 , The results of the forecast are calculated by finding the average midpoint
, The results of the forecast are calculated by finding the average midpoint 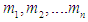 for the periods and by formula
for the periods and by formula 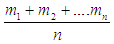 this model that has been presented is called a fuzzy time series model of the first order, and Chen has provided models The steps for finding a prognosis are the same as the previous method with a difference in the formation of the fuzzy relationships.
this model that has been presented is called a fuzzy time series model of the first order, and Chen has provided models The steps for finding a prognosis are the same as the previous method with a difference in the formation of the fuzzy relationships.4.2. Fuzzy C-means Method Review
- The FCM method is also called Fuzzy ISODATA, which was proposed by Bezdek in 1981 [44], [45].The algorithm for this method represents a clustering technique separated from Hard c-means (HCM), so the HCM algorithm is based mainly on the philosophy of Crisp Set, which uses the strong hard partitioning of data points, so that the deterministic determination of the affiliation of these points: whether it belongs For a specific cluster or not, as for the FCM algorithm, it is based on the philosophy of fuzzy logic, which mainly depends on the idea of gradual belonging and fuzzy partitioning, which allows each data point to belong to a cluster with a specific degree to an organic degree, and thus each data point can belong to several clusters in the n One with different degrees of membership falls in the period [0,1].If we assume that the data set
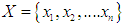 is a finite subset of the set of real numbers. Let us assume that c is the number of clusters and it is an integer such that
is a finite subset of the set of real numbers. Let us assume that c is the number of clusters and it is an integer such that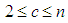 , so the FCM algorithm splits the data set X into c from fuzzy clusters, so that the data in the same set are as similar as possible and differ from other different groups as much as possible.Thus, the fuzzy hash of the datasets X can be represented by the membership matrix U with dimensions
, so the FCM algorithm splits the data set X into c from fuzzy clusters, so that the data in the same set are as similar as possible and differ from other different groups as much as possible.Thus, the fuzzy hash of the datasets X can be represented by the membership matrix U with dimensions 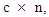 so each entry in the U matrix is denoted by
so each entry in the U matrix is denoted by 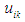 and is within the range [0,1].
and is within the range [0,1].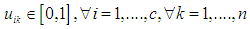 | (4.2) |
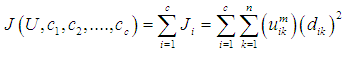 Where
Where 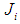 is the target function within the cluster i
is the target function within the cluster i 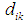 is the Euclidean distance between the data point
is the Euclidean distance between the data point 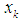 and the center
and the center 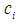 , and the J function is reduced according to the following restrictions [46]:
, and the J function is reduced according to the following restrictions [46]: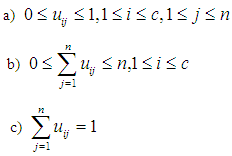 | (4.3) |
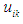 , it represents the degree of membership of the data point
, it represents the degree of membership of the data point 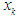 to the center of the cluster
to the center of the cluster 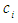 and is within the range [0, 1] and that the parameter M: is Membership Weighting Exponent,
and is within the range [0, 1] and that the parameter M: is Membership Weighting Exponent, 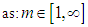 , In order to achieve a reduction of the objective function, there are two conditions represented by the two equations as follows:
, In order to achieve a reduction of the objective function, there are two conditions represented by the two equations as follows: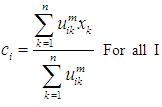 | (4.4) |
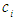 the center of the cluster i and i = 1, 2, 3…c
the center of the cluster i and i = 1, 2, 3…c 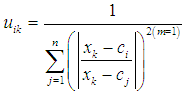 | (4.5) |
 The second step: Divide the comprehensive set of several clusters using the FCM algorithm, which will produce clusters containing a set of data that are similar to each other
The second step: Divide the comprehensive set of several clusters using the FCM algorithm, which will produce clusters containing a set of data that are similar to each other 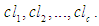 The third step: Defining the fuzzy groups on the global set suppose that
The third step: Defining the fuzzy groups on the global set suppose that 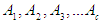 is the fuzzy groups, so they can be defined in the form:
is the fuzzy groups, so they can be defined in the form: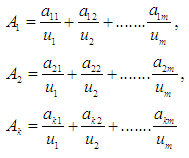 Whereas
Whereas 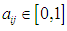 and
and 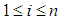 and
and 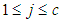 And
And 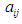 represents the degree of membership for the assertive period
represents the degree of membership for the assertive period 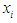 in the
in the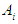 it is a component of the membership matrix U.Fourth step: fuzzfied the data. This step is done by testing each cluster in the form of a fuzzy group.
it is a component of the membership matrix U.Fourth step: fuzzfied the data. This step is done by testing each cluster in the form of a fuzzy group.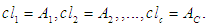 Each value entered represents the highest degree of affiliation within a given cluster, which appears in the membership matrix that was mentioned previously, is fuzzfied to the fuzzy group equal to that cluster. Let us say that the entered value of
Each value entered represents the highest degree of affiliation within a given cluster, which appears in the membership matrix that was mentioned previously, is fuzzfied to the fuzzy group equal to that cluster. Let us say that the entered value of 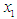 for the year 1970 falls within the first cluster, then
for the year 1970 falls within the first cluster, then 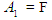 (1970). Thus for all the entries, the historical data are fuzzfied according to his fuzzy group.As for the remaining steps (from the fifth step to the last they are similar to the previously mentioned steps within the Chen method and for the first and second order.
(1970). Thus for all the entries, the historical data are fuzzfied according to his fuzzy group.As for the remaining steps (from the fifth step to the last they are similar to the previously mentioned steps within the Chen method and for the first and second order.4.3. Suggested Method for Predicting Using FCM Review
- Through our study of the fuzzy meshing methods such as Chen method and the fuzzy C-medium FCM method, and we obtained the results of prediction for it, and in order to develop the previous methods to obtain better results for the values of the prognosis according to the ideas studied in this research, we proposed a method that includes the same previous steps except for the step for reconstructing the fuzzy relations groups and is as follows : Reconstructing the fuzzy relationships of the group of fuzzy groups is the most important step in this method, as the relationships between the group of fuzzy groups are raised (trimming) the relationships between the group of fuzzy groups are rebuilt according to special rules, meaning that if
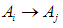 and the predictive value of the group of uncertain
and the predictive value of the group of uncertain 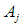 depends on the group
depends on the group 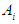 then Relationships group promises to be formed by the proposed relationship
then Relationships group promises to be formed by the proposed relationship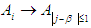 So we had the relationships
So we had the relationships 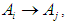
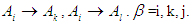 Therefore, the results of the prediction will be close to the real results. If we take the example the new relationships will be according to our proposal in the form
Therefore, the results of the prediction will be close to the real results. If we take the example the new relationships will be according to our proposal in the form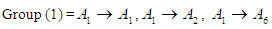 Then
Then 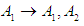 This method is somewhat similar to the median method as one of the measures of central tendency in statistics.
This method is somewhat similar to the median method as one of the measures of central tendency in statistics.5. Application Phase, Results and Discussion
5.1. Introduction
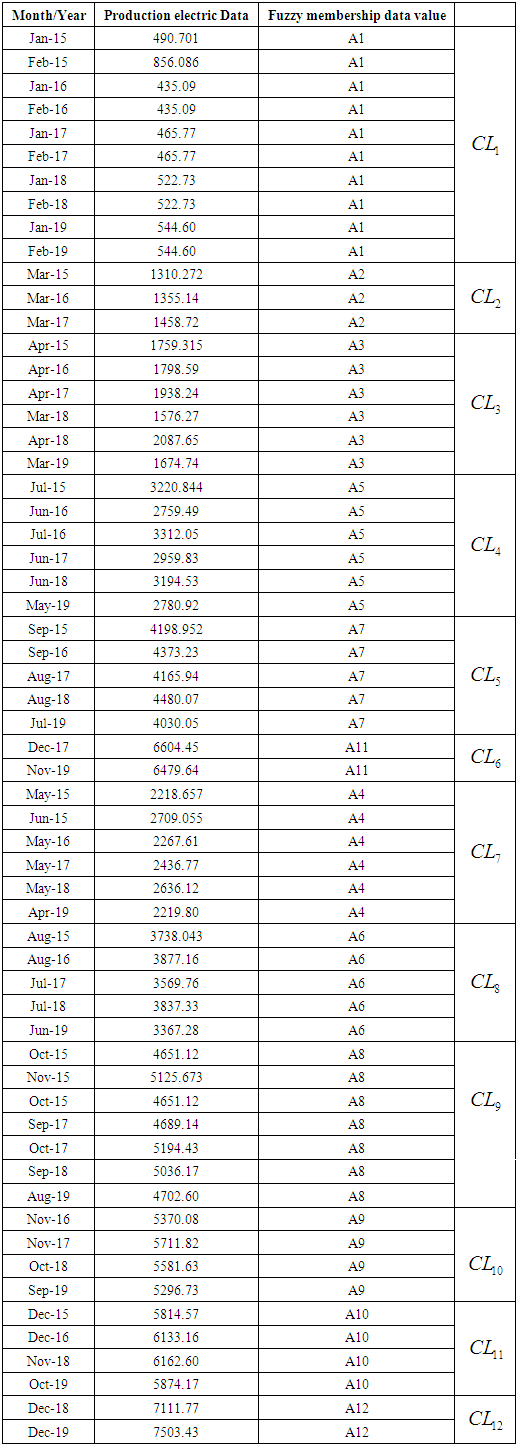
- This section includes three applications of Chen method and Fuzzy Time Series c-means and Suggested Method on data representing the amount of production and consumption electric for the years (2015_2016). The first application deals with the Chen method, the second application of the cluster method is the fuzzy c-medium method FCM, and finally a Suggested method for forecasting using FCM. Using different organic functions to find the organic values of the elements in the fuzzy groups, and also using the fuzzy relationships of the first and second order, and the extent of the influence of all these elements on the results of the prediction was clarified.The ready-made program (MATLAB 2012), excel was used to divide the data into the required clusters by FCM method, and also to find and plot the values of membership scores and plot fuzzy time series.
5.2. Data Description
- The data used in the application represent the amount of production and consumption electric in china for the years (Jan 2015_Dec 2019) and its range ranges between (400_6900) GWh. From observing the data, we find that it is characterized by instability and varies from month to month randomly. We have dealt with this data because of the importance and great impact of production and consumption electric. On our daily life and its impact on the economy, agriculture, etc. as well as floods, Figure (1) and figure (2) represents a chart of the time series of production electric and consumption for each month.
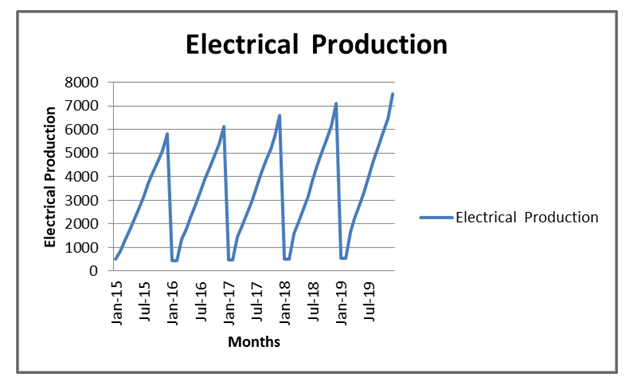 | Figure 1. Production electric Time series of the amount of electricity production from the time period (2015-2019) |
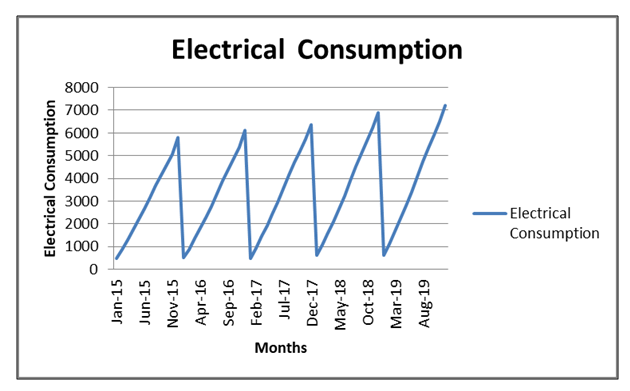 | Figure 2. Consumption electric Time series of the amount of electricity consumption from the time period (2015-2019) |
5.3. Model Evaluation
- The process of evaluating models is intended to evaluate the field suitability of the model for the pattern in which the series data is running or the accuracy of the model in predicting the values of the current and future series, and there are many measures of the suitability of the model all depend on the degree of error, which is the difference between the actual value of the series at a specific time And the string value that the model expected at that time. In this study, we will rely on the following methods to compare the two models used in this paper to find out which one is more accurate in prediction.
5.3.1. Mean Absolute Percentage Error (MAPE)
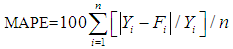 | (5.1) |
5.3.2. Mean Absolute Deviation (MAD)
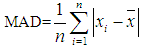 | (5.2) |
5.4. Result Chen Method and Discussion
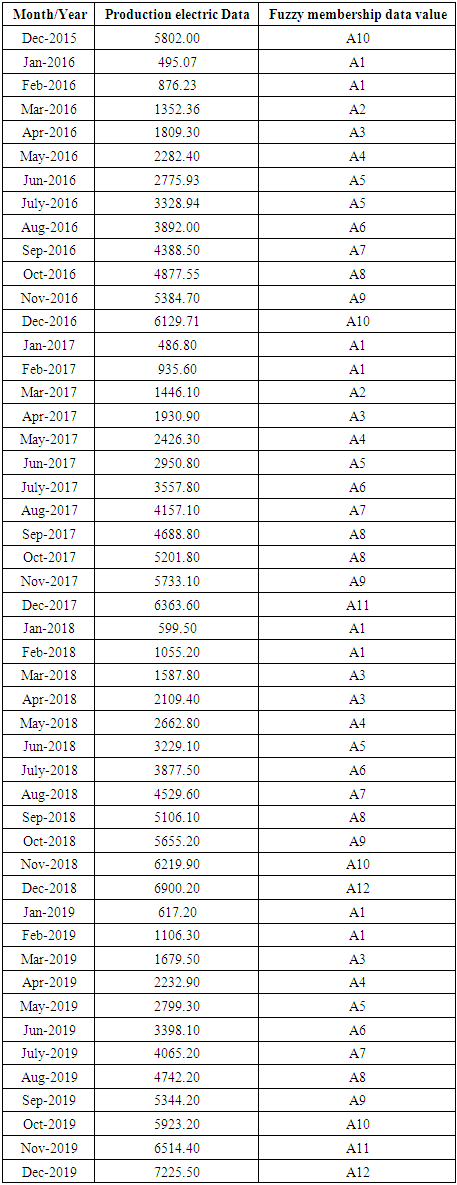
- In this method, we will find forecast values for the state of electricity production in the period between December 2015 and December 2019.The universal set U must be divided into several equal intervals. In our case, this set U is divided into twelve intervals equally.The first Step; define the global event
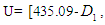
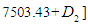 where
where 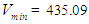 is the smallest value (Jan 2019),
is the smallest value (Jan 2019), 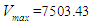 is the greatest value (Dec- 2019),
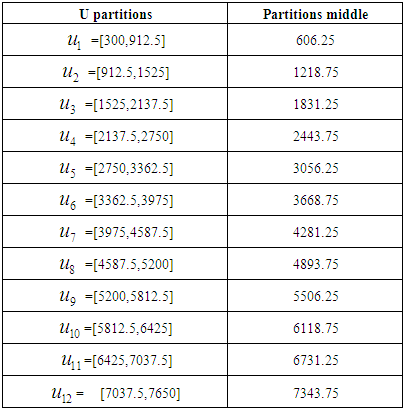
is the greatest value (Dec- 2019), 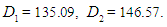 Thus, the universal set U will be as follows: U= {300, 7650}.And then divide U into equal intervals in length, which is in the table 5.4.1 below:
Thus, the universal set U will be as follows: U= {300, 7650}.And then divide U into equal intervals in length, which is in the table 5.4.1 below:
|
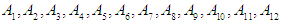 As linguistic expressions in the form
As linguistic expressions in the form 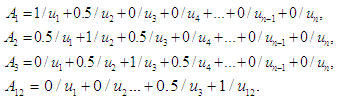 And the value of the organic function for the fuzzy groups is calculated as
And the value of the organic function for the fuzzy groups is calculated as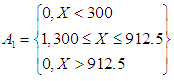 And so on for the rest of the groups.The third step, which is fuzzification the historical data, was on the basis of the highest degree of membership within the periods. Let us take the first value, because it has the highest degree of affiliation in the period
And so on for the rest of the groups.The third step, which is fuzzification the historical data, was on the basis of the highest degree of membership within the periods. Let us take the first value, because it has the highest degree of affiliation in the period 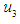 , so (1970) F is in the group
, so (1970) F is in the group 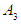 and the second value is, it has the highest degree of affiliation in the period
and the second value is, it has the highest degree of affiliation in the period 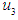 also, so (1971) F is fuzzifed In the
also, so (1971) F is fuzzifed In the 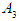 group, and so on for the rest of the historical values, as shown in Table 5.4.2 below.
group, and so on for the rest of the historical values, as shown in Table 5.4.2 below.
|
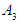 and F(May-2016) is fuzzfied into
and F(May-2016) is fuzzfied into 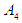 , so
, so 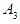 relates to
relates to 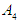 and we denote it by the symbol
and we denote it by the symbol 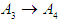 , and F(May-2016) is fuzzfied into
, and F(May-2016) is fuzzfied into 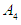 so
so 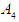 relates to
relates to 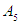 so it is denoted by
so it is denoted by 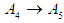 .The fifth step represents the establishment of groups of fuzzy relationships. From Table 5.4.3, we notice that the fuzzy groups have a fuzzy relationship with more than one group, so the groups are merged or grouped on the right side, noting that no fuzzy group is repeated on the right side, so we notice that the group
.The fifth step represents the establishment of groups of fuzzy relationships. From Table 5.4.3, we notice that the fuzzy groups have a fuzzy relationship with more than one group, so the groups are merged or grouped on the right side, noting that no fuzzy group is repeated on the right side, so we notice that the group 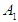 It has a relationship.With
It has a relationship.With 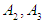 and becomes the first group in the form: Group (1):
and becomes the first group in the form: Group (1): 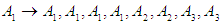 The following table 5.4.3 shows groups of fuzzy relationships
The following table 5.4.3 shows groups of fuzzy relationships
|
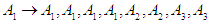 ,In this group we can find the value by Partitions middle.Contains mid intervals of U partitions table 5.4.1.Forecasting value Example: 5814, 57*1/2 "of A1"+1875*1/2 "of A2"+ 2925*0 "of A3"+...+ 7125*0 "of A12"=5320.3125. This forecasted value looks much greater than the real value in Jan-2016 = 453, 09. That’s means we will see high MAPE and MAD. We will see the next method in the next section.Table 5.4.4 and Table 5.4.5 below show the actual and forecasted values of production and consumption electric for period from January 2016 to December 2019 in GWh the result has been rounded to the nearest integer.
,In this group we can find the value by Partitions middle.Contains mid intervals of U partitions table 5.4.1.Forecasting value Example: 5814, 57*1/2 "of A1"+1875*1/2 "of A2"+ 2925*0 "of A3"+...+ 7125*0 "of A12"=5320.3125. This forecasted value looks much greater than the real value in Jan-2016 = 453, 09. That’s means we will see high MAPE and MAD. We will see the next method in the next section.Table 5.4.4 and Table 5.4.5 below show the actual and forecasted values of production and consumption electric for period from January 2016 to December 2019 in GWh the result has been rounded to the nearest integer.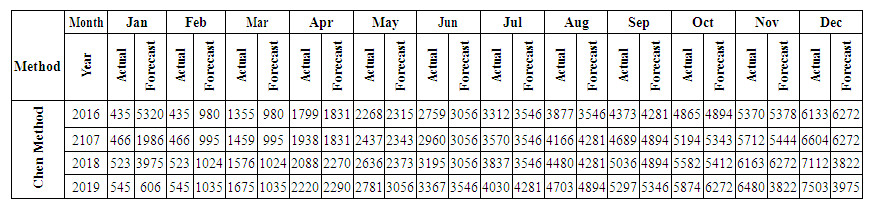 | Table 5.4.4. Actual and forecasted values of production electric in GWh |
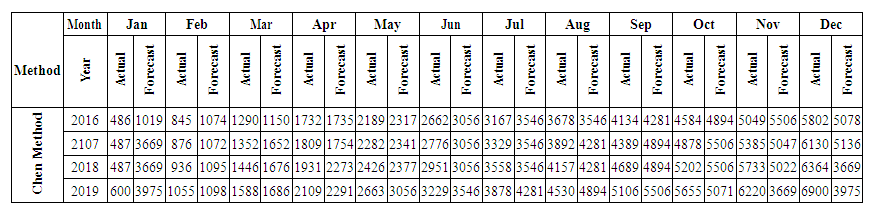 | Table 5.4.5. Actual and forecasted values of consumption electric in GWh |
5.5. Result Fuzzy c-mean (FCM) Method and Discussion
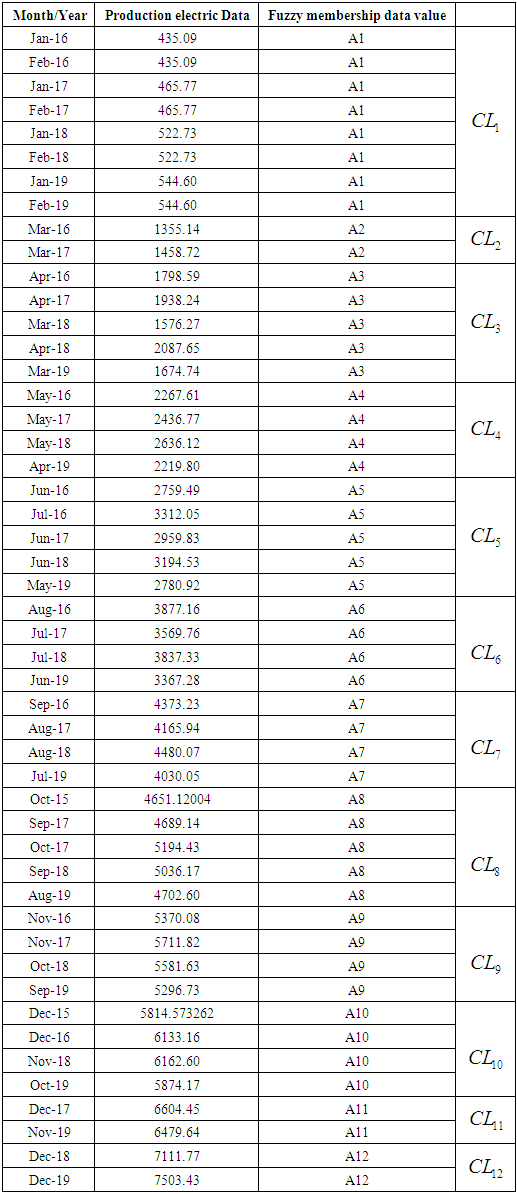
- In this model we will present the application in finding the predicted values of the data shown, and as we mentioned in section 5.4 the method of finding the clusters that we will use in finding the values of the prognosis and the number of clusters (5_12) clusters and by using the Gaussian natural membership function for the first order.The first step is to define the data set. The second step is to determine the number of clusters and find the group of each cluster. We have dealt with the number of clusters (12). As for the rest of the results, we will mention them in an appendix of the results. And using MATLAB or excel program, the ten clusters and its contents were determined from the data used, and the results were as shown in Table 5.5.1 below:
|
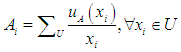 | (5.3) |
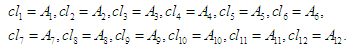 We see that the third value falls within the second cluster, and accordingly it is fuzzfied
We see that the third value falls within the second cluster, and accordingly it is fuzzfied 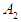 . The fourth value falls within the third cluster
. The fourth value falls within the third cluster 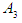 and so on for the rest of the data, as in Table (5.5.1) above.The fifth step is distinguishing fuzzy relationships: From the definition of fuzzy relationships, we can extract the relationships between fuzzy groups; the following table (5.5.2) shows the fuzzy relationships.
and so on for the rest of the data, as in Table (5.5.1) above.The fifth step is distinguishing fuzzy relationships: From the definition of fuzzy relationships, we can extract the relationships between fuzzy groups; the following table (5.5.2) shows the fuzzy relationships.
|
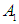 has a fuzzy relationship with more than one group. One, the groups are merged or combined on the right side, and no fuzzy group can appear on the right side for more than one time only, so the first group is
has a fuzzy relationship with more than one group. One, the groups are merged or combined on the right side, and no fuzzy group can appear on the right side for more than one time only, so the first group is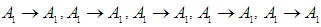
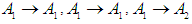 So,Group (1):
So,Group (1): 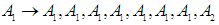 And the second group is
And the second group is 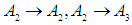 Group (2):
Group (2): 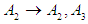 And Third group is
And Third group is 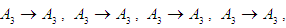
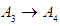 Group (3):
Group (3): 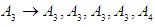 And fourth group is
And fourth group is 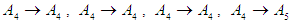 Seventh and final step is to raise the fuzziness to find the results of the forecast, and this step depends on the previous step. From the first group
Seventh and final step is to raise the fuzziness to find the results of the forecast, and this step depends on the previous step. From the first group 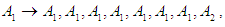 In this group we can find the value by Partitions middle.Contains mid intervals of U partitions table 5.4.1.Forecasting value Example: 606.25*0 "of A1"+1218.75*0 "of A2"+ 1831.25*0 "of A3"+...+ 7343.75*0 "of A12"=6044. This forecasted value looks much greater than the real value in Jan-2016 = 453, 09. That's why the suggested method proposes to adjust these values. We will see the full suggested method in the next section high accurate more than this method and previous method.Table 5.5.3 and Table 5.5.4 below show the actual and forecasted values of production and consumption electric for period from January 2016 to December 2019 in GWh the result has been rounded to the nearest integer.
In this group we can find the value by Partitions middle.Contains mid intervals of U partitions table 5.4.1.Forecasting value Example: 606.25*0 "of A1"+1218.75*0 "of A2"+ 1831.25*0 "of A3"+...+ 7343.75*0 "of A12"=6044. This forecasted value looks much greater than the real value in Jan-2016 = 453, 09. That's why the suggested method proposes to adjust these values. We will see the full suggested method in the next section high accurate more than this method and previous method.Table 5.5.3 and Table 5.5.4 below show the actual and forecasted values of production and consumption electric for period from January 2016 to December 2019 in GWh the result has been rounded to the nearest integer.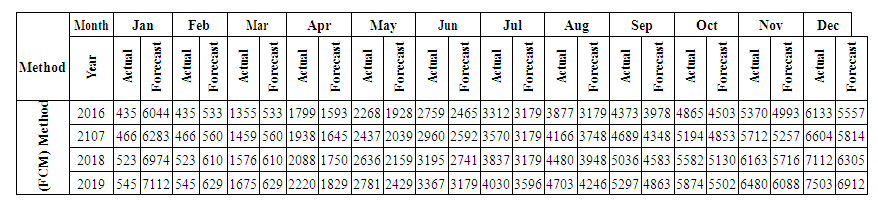 | Table 5.5.3. Actual and forecasted values of production electric in GWh |
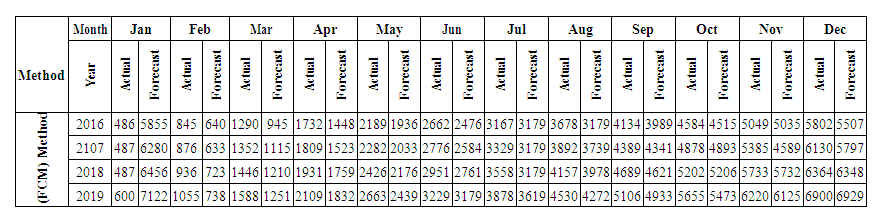 | Table 5.5.4. Actual and forecasted values of consumption electric in GWh |
5.6. Result Suggested Method for Predicting Using (FCM) and Discussion
- The working steps for this model are similar to the methodology steps for the model Fuzzy c-mean method, and by using new membership function for the first order.The first step is to define the data set. The second step is to determine the number of clusters and find the group of each the sixth and final step is to raise the fuzziness to find the program, the twelve clusters and its contents were determined from the data from January 2015 to December 2016 because we use time-invariant fuzzy time series see section 3 in this step the data will be classified based on the primes and even numbers, so that the primes and the even numbers are arranged respectively, and the results were as shown in Table (5.6.1) below:
|
 has a fuzzy relationship with more than one group. One, the groups are merged or combined on the right side, and no fuzzy group can appear on the right side for more than one time only, then Relationships group promises to be formed by the proposed relationship
has a fuzzy relationship with more than one group. One, the groups are merged or combined on the right side, and no fuzzy group can appear on the right side for more than one time only, then Relationships group promises to be formed by the proposed relationship
|
 So we had the relationships
So we had the relationships 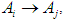
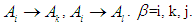 So the first group is
So the first group is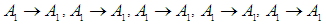
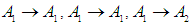 So,Group (1):
So,Group (1): 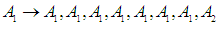 And the second group is
And the second group is 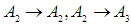 Group (2):
Group (2): 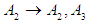 And Third group is
And Third group is 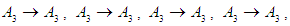
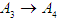 Group (3):
Group (3): 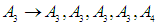 Seventh and final step is to raise the fuzziness to find the results of the forecast, and this step depends on the previous step.From the first group:
Seventh and final step is to raise the fuzziness to find the results of the forecast, and this step depends on the previous step.From the first group: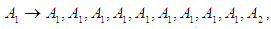 In this group we can find the value by Partitions middle,Contains middle intervals of U partitions table 5.4.1.Forecasting value Example: 606.25*8/9 "of A1"+1218.75*1/9 "of A2"+ 2925*0 "of A3"+...+ 7125*0 "of A12"=563.5059. This forecasted value looks near.The real value in Jan-2016 = 453, 09. Here in this method we calculated based on different time that mean we calculate the forecast by looking to January of year 2015 That's we see the suggested method most near from the real value.Table 5.6.3 and Table 5.6.4 below show the actual and forecasted values of production and consumption electric for period from January 2016 to December 2019 in GWh the result has been rounded to the nearest integer.
In this group we can find the value by Partitions middle,Contains middle intervals of U partitions table 5.4.1.Forecasting value Example: 606.25*8/9 "of A1"+1218.75*1/9 "of A2"+ 2925*0 "of A3"+...+ 7125*0 "of A12"=563.5059. This forecasted value looks near.The real value in Jan-2016 = 453, 09. Here in this method we calculated based on different time that mean we calculate the forecast by looking to January of year 2015 That's we see the suggested method most near from the real value.Table 5.6.3 and Table 5.6.4 below show the actual and forecasted values of production and consumption electric for period from January 2016 to December 2019 in GWh the result has been rounded to the nearest integer.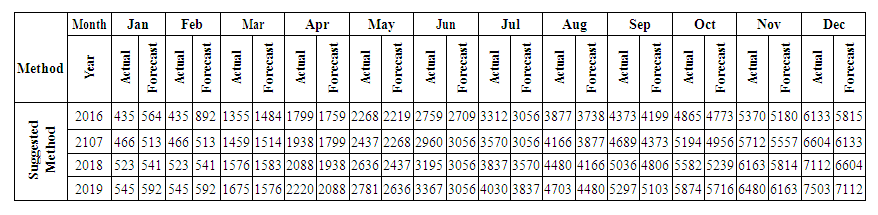 | Table 5.6.3. Actual and forecasted values of production electric in GWh |
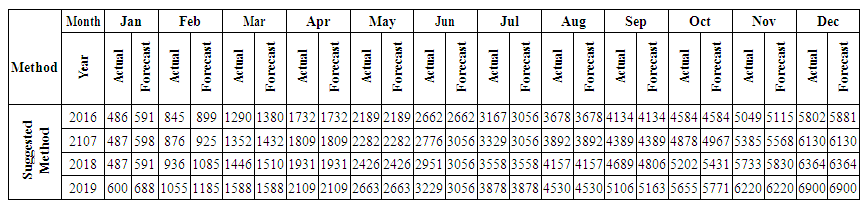 | Table 5.6.4. Actual and forecasted values of consumption electric in GWh |
6. Conclusions
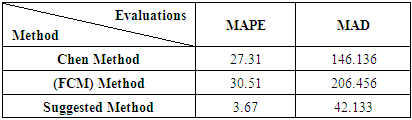
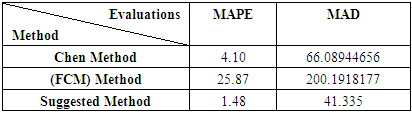
- The forecasts obtained utilizing Chen method and Fuzzy Time Series c-means and Suggested Method is discussed in this paper. The aforementioned methods require only the historical data series of electricity production and consumption to build the forecast. This can be considered as an important advantage, because the effort and cost linked to the data mining are very limited. These historical time series data are analyzed to understand the past and predict the future. Mean Absolute Percentage Error the mean absolute deviation.The results of predictive metrics of electricity production indicated that the Mean Absolute Percentage Error ranged from 3.67 (Suggested Method) to 30.51 Fuzzy Time Series c-means and mean absolute deviation ranged from 42.133 (Suggested Method) to 146.136 Chen method.Chen Method performed closed to the Suggested Method but Fuzzy Time Series c-means deviated a lot (Table 6.1), (Table 6.2). So, this criterion clearly indicated the superiority of Suggested Method in forecasting the production of electricity and consumption electric during 2016-2019. Similarly, the Suggested Method gave the lowest value thus performed best followed more than Chen method and Fuzzy Time Series c-means. Fuzzy Time Series c-means performed the worst in all cases.
|
|
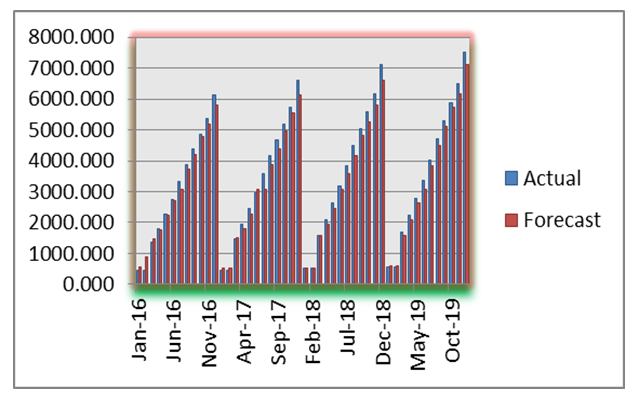 | Figure 3. Actual and forecasted values of Suggested Method for production electric |
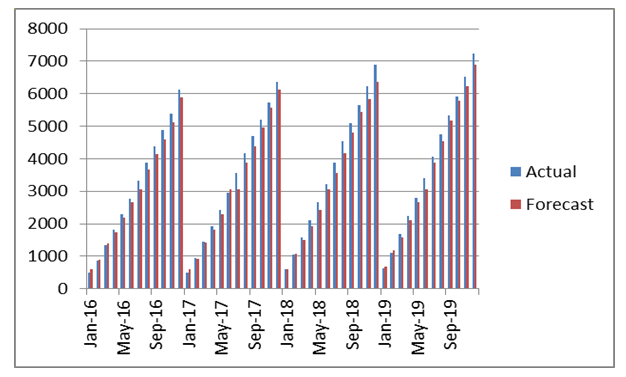 | Figure 4. Actual and forecasted values of Suggested Method for consumption electric |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML