-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2020; 10(2): 55-61
doi:10.5923/j.ajms.20201002.04

When Sciences Overlaps: A Matching Game under a Graph Concept
Essam El-Seidy , Maan T. Alabdullah , Shahd H. Alkaraz
Department of Mathematics, Faculty of Science, Ain Shams University, Cairo, Egypt
Correspondence to: Shahd H. Alkaraz , Department of Mathematics, Faculty of Science, Ain Shams University, Cairo, Egypt.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Initially, we provide basic knowledge of definitions and concepts related to the concept of matching in the graph. We are studying a model of games based on two players who take turns adding edges to 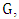 this process eventually produces a maximal matching of the graph. We call the first Maximizer and second player Minimizer. The first aims to get a final matching to be large while the second one wants to reduce it. Maximizer wins if he manages a maximal matching while Minimizer wins if he can prevent him from doing this. The matcher number
this process eventually produces a maximal matching of the graph. We call the first Maximizer and second player Minimizer. The first aims to get a final matching to be large while the second one wants to reduce it. Maximizer wins if he manages a maximal matching while Minimizer wins if he can prevent him from doing this. The matcher number 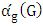 is the number of edges chosen when both players play optimally, while the matching number
is the number of edges chosen when both players play optimally, while the matching number 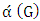 is the number of maximum matching edges. In this research we study the relationship between
is the number of maximum matching edges. In this research we study the relationship between 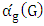 and
and 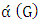 . And we also prove some results on types of graph.
. And we also prove some results on types of graph.
Keywords: Maximal matching, Maximum matching, Matching, Matcher game
Cite this paper: Essam El-Seidy , Maan T. Alabdullah , Shahd H. Alkaraz , When Sciences Overlaps: A Matching Game under a Graph Concept, American Journal of Mathematics and Statistics, Vol. 10 No. 2, 2020, pp. 55-61. doi: 10.5923/j.ajms.20201002.04.
Article Outline
1. Introduction
- As the title suggests, this research is about games on graphs. At first sight, the topic may suggest lots of fun since games are widely recognized as amusing. But the reader should keep in mind that this is a collection of mathematical results and as such has a moderate fun impact.Matching in graphs has been an important topic and has a lot of applications for solving problems. It is used to solve Important problems. This can be generalized to solve any problem that can represented as a graph, we will discuss the general matching idea and Matching in graphs.The matcher game is related to the growing family of competition parameters or competitive optimization games on graphs and hypergraphs. For example, Phillips and Slater introduced a game where two players alternate adding vertices of
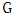 to an independent set until it becomes a maximal independent set. One player wants the final set to be large; the other wants it to be small. More recently, Cranston et al. [1] introduced a game where the players alternate adding edges of
to an independent set until it becomes a maximal independent set. One player wants the final set to be large; the other wants it to be small. More recently, Cranston et al. [1] introduced a game where the players alternate adding edges of 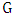 to a matching until it becomes a maximal matching. Theirs is equivalent to the game of played on the line graph and is a very different game to ours. Probably the best-known such parameter is the game chromatic number, which was introduced by Brams for planar graphs (cf. [2]) and independently by Bodlaender [3] for general graphs, and for list colorings by Borowiecki et al. [4]. There is also work on domination [5,6], transversals in hypergraphs [7,8] and more.We denote the matching number of graphs
to a matching until it becomes a maximal matching. Theirs is equivalent to the game of played on the line graph and is a very different game to ours. Probably the best-known such parameter is the game chromatic number, which was introduced by Brams for planar graphs (cf. [2]) and independently by Bodlaender [3] for general graphs, and for list colorings by Borowiecki et al. [4]. There is also work on domination [5,6], transversals in hypergraphs [7,8] and more.We denote the matching number of graphs 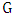 by
by 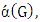 and define the lower matching number
and define the lower matching number 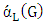 as the minimum cardinality of a maximal matching of
as the minimum cardinality of a maximal matching of 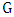 .The main goal is to study the values of the game that fall between
.The main goal is to study the values of the game that fall between 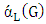 and
and 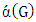 . where we have two cases either Minimizer starts and the two values are equal and therefore the matching number is not interesting so our focus in this research is on the Max-start matcher number which we simply call the matcher number. There we show that, while for bipartite graphs the matcher number equals the matching number, in general
. where we have two cases either Minimizer starts and the two values are equal and therefore the matching number is not interesting so our focus in this research is on the Max-start matcher number which we simply call the matcher number. There we show that, while for bipartite graphs the matcher number equals the matching number, in general 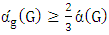 , and we characterize the graphs
, and we characterize the graphs 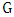 for which
for which 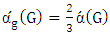 . We also investigate the relationship with the lower matching number, showing that
. We also investigate the relationship with the lower matching number, showing that 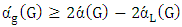 . We conclude with some sufficient conditions for
. We conclude with some sufficient conditions for 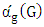 to be half the order.
to be half the order.1.1. Introduction of the Matching Game
- In this research we introduce the matching game. This is played on undirected graph
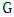 by two players, called Maximizer and Minimizer, who take turns in constructing a matching of
by two players, called Maximizer and Minimizer, who take turns in constructing a matching of 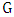 . Each round, one player chooses a vertex
. Each round, one player chooses a vertex 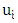 with at least one neighbor not previously chosen, and the other player chooses a vertex
with at least one neighbor not previously chosen, and the other player chooses a vertex 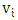 not previously chosen that is a neighbor of
not previously chosen that is a neighbor of 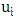 . This process continues until no more play is possible; that is, the edges
. This process continues until no more play is possible; that is, the edges 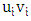 form a maximal matching of
form a maximal matching of 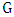 . Maximizer wishes to maximize the number of edges in this matching, while Minimizer wishes to minimize it. The Max-start matcher number
. Maximizer wishes to maximize the number of edges in this matching, while Minimizer wishes to minimize it. The Max-start matcher number 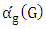 of
of 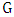 is the number of edges in the matching when Maximizer starts and both players play optimally, while the Min-start matcher number
is the number of edges in the matching when Maximizer starts and both players play optimally, while the Min-start matcher number 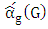 of
of 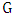 is the number of edges chosen when Minimizer starts and both players play optimally.For notation and graph-theory terminology not defined herein, we in general follow [9]. We denote the degree of a vertexin a graph
is the number of edges chosen when Minimizer starts and both players play optimally.For notation and graph-theory terminology not defined herein, we in general follow [9]. We denote the degree of a vertexin a graph 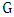 by
by 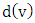 . The minimum degree among the vertices of
. The minimum degree among the vertices of 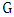 is denoted by
is denoted by 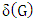 .The following are some important concepts:• A matching M: is a set of edges in
.The following are some important concepts:• A matching M: is a set of edges in 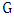 no two of which are adjacent.• A perfect matching M: if every vertex of
no two of which are adjacent.• A perfect matching M: if every vertex of 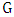 is incident to an edge of
is incident to an edge of 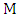 .• Maximal matching: if no other edges of
.• Maximal matching: if no other edges of 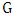 can be added to
can be added to 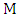 .• Maximum matching: are largest maximal matching.• Matching number
.• Maximum matching: are largest maximal matching.• Matching number 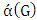 : is number of edges in the maximum matching of
: is number of edges in the maximum matching of 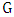 .• Lower matching number
.• Lower matching number 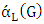 : is the minimum cardinality of a maximal matching of
: is the minimum cardinality of a maximal matching of 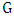 .• If
.• If 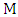 is a matching in
is a matching in 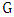 , then a vertex is
, then a vertex is 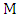 -matched or covered by
-matched or covered by 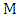 if it is incident with an edge of
if it is incident with an edge of 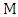 ; otherwise, the vertex is
; otherwise, the vertex is 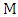 -unmatched.• A path or cycle is
-unmatched.• A path or cycle is 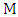 -alternating of its edges are alternately in and not in
-alternating of its edges are alternately in and not in 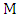 .• Max start matcher number
.• Max start matcher number 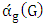 : is the number of edges in the matching when Maximizer starts and both players play optimally• Min start matcher number
: is the number of edges in the matching when Maximizer starts and both players play optimally• Min start matcher number  : is the number of edges chosen when Minimizer starts and both players play optimally.The following figure shows the difference between Maximal matching and Maximum matching.
: is the number of edges chosen when Minimizer starts and both players play optimally.The following figure shows the difference between Maximal matching and Maximum matching.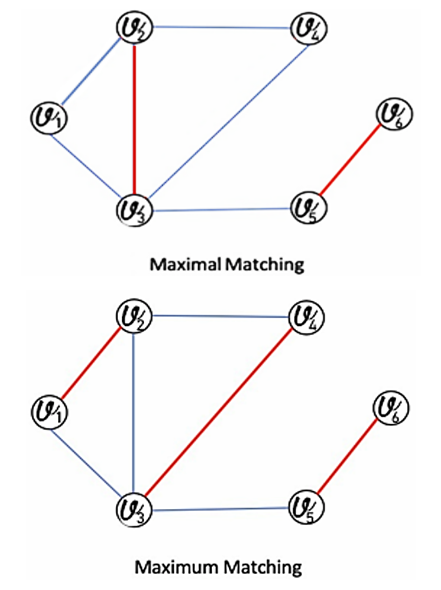 | Figure 1. The difference between Maximal matching and Maximum matching |
2. The Minimizer Starts the Game
- We start by showing that the Min-start matcher number of a graph is precisely the matching number of the graph. We shall need the following trivial well-known preliminary lemma. Lemma 1. For every graph
 , every non-isolated vertex is incident with an edge that belongs to some maximum matching of
, every non-isolated vertex is incident with an edge that belongs to some maximum matching of  [10]. In the following graph we note that every vertex is incident with an edge belong to a maximum matching
[10]. In the following graph we note that every vertex is incident with an edge belong to a maximum matching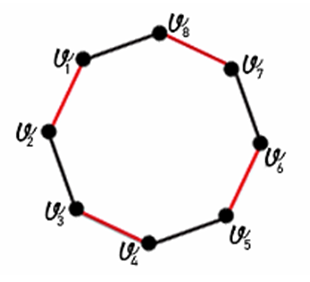 | Figure 2. Example of Lemma 1 |
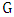 is a graph, then have
is a graph, then have 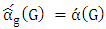 .Proof.We show that Maximizer has a strategy that guarantees that the Min-start matcher game always finishes with a maximum matching, implying that
.Proof.We show that Maximizer has a strategy that guarantees that the Min-start matcher game always finishes with a maximum matching, implying that 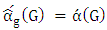 . Suppose that Minimizer chooses vertex
. Suppose that Minimizer chooses vertex 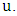 By Lemma 1, the vertex
By Lemma 1, the vertex 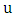 is incident with an edge, say
is incident with an edge, say 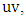 that belongs to some maximum matching,
that belongs to some maximum matching, 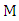 say, In
say, In 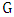 . So, Maximizer chooses vertex
. So, Maximizer chooses vertex 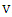 . Then let
. Then let 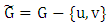 . Note that
. Note that 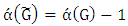 , while by induction we have
, while by induction we have 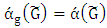 , then
, then 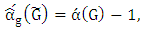 and from it
and from it 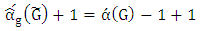 and then
and then 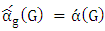 .
.3. The Maximizer Starts the Game
- For the remainder of the paper we study the Max-start matcher game. Here is an example:Lemma 2.For the path
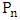 with
with 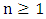 it holds that
it holds that 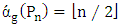 . For the cycle
. For the cycle 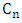 with
with 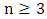 it holds that
it holds that 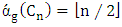 [10].For the cycle
[10].For the cycle 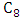 and
and 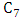 , we find
, we find 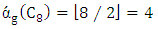 and
and 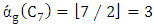 as shown in Figure 3.
as shown in Figure 3.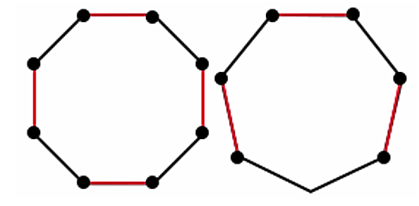 | Figure 3. Max start matcher number for the cycle  |
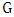 is a graph with minimum degree at least two that contains a unique maximum matching, then
is a graph with minimum degree at least two that contains a unique maximum matching, then 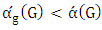 .Proof.Let
.Proof.Let 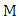 be the unique maximum matching in
be the unique maximum matching in 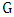 . By Lemma 1, every vertex is incident with
. By Lemma 1, every vertex is incident with 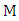 ; that is,
; that is, 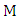 is a perfect matching. Let
is a perfect matching. Let 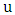 be the first vertex chosen by Maximizer. Since
be the first vertex chosen by Maximizer. Since 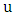 has degree at least two, Minimizer can respond by choosing a vertex
has degree at least two, Minimizer can respond by choosing a vertex 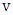 such that
such that 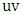 is not in
is not in 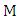 ; thus, the maximal matching that is constructed will not be
; thus, the maximal matching that is constructed will not be 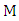 . It follows that
. It follows that 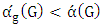 .Definition: We define a vertex of a graph
.Definition: We define a vertex of a graph 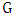 as liberal if it is not isolated and every edge incident with
as liberal if it is not isolated and every edge incident with 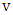 belongs to some maximum matching in
belongs to some maximum matching in 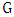 .An example in the following figure we call the vertexes
.An example in the following figure we call the vertexes 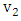 and
and 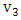 liberal vertex, while the vertexes
liberal vertex, while the vertexes 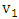 and
and 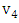 are not.
are not.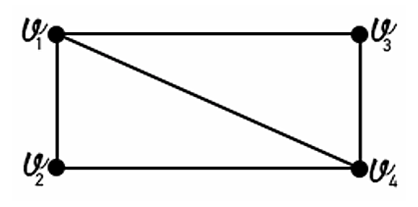 | Figure 4. Graph that contains liberal vertexes |
 be a hereditary graph family such that every nonempty graph in
be a hereditary graph family such that every nonempty graph in  has a liberal vertex. Then for all
has a liberal vertex. Then for all  it holds that
it holds that 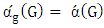 .Proof. The proof is by induction. If
.Proof. The proof is by induction. If 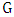 has no edges, then
has no edges, then 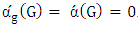 . If
. If 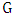 is nonempty, then by assumption there is a liberal vertex in
is nonempty, then by assumption there is a liberal vertex in 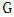 , say
, say 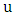 . Maximizer chooses this as his first move. Let
. Maximizer chooses this as his first move. Let 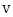 be the response of Minimizer and let
be the response of Minimizer and let 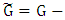
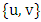 . Note that
. Note that 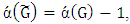 while by induction we have
while by induction we have 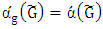 since
since 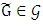 , then
, then 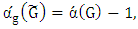 and from it
and from it 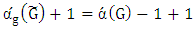 and then
and then 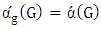 .Note from Figure 4 for liberal vertex
.Note from Figure 4 for liberal vertex 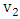 we have
we have 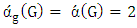 .For example, it is immediate that any end-vertex of a graph is liberal; thus trees/forests are examples of the above situation. We show next that isolate-free graphs without perfect matchings always have a liberal vertex (see [11]). Lemma 5.If
.For example, it is immediate that any end-vertex of a graph is liberal; thus trees/forests are examples of the above situation. We show next that isolate-free graphs without perfect matchings always have a liberal vertex (see [11]). Lemma 5.If 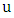 is a non-isolated vertex and there exists a maximum matching
is a non-isolated vertex and there exists a maximum matching  where
where  is
is 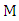 -unmatched, then
-unmatched, then 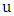 is liberal.Proof. As in the proof of Lemma 1, every neighbor
is liberal.Proof. As in the proof of Lemma 1, every neighbor 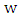 of
of 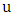 is incident with an edge of
is incident with an edge of 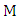 , say
, say 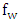 , and
, and 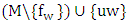 is a maximum matching in
is a maximum matching in 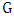 containing
containing 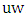 . That is,
. That is, 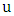 is liberal.
is liberal. 3.1. Bipartite Graphs
- We conclude below some properties to see the relation between
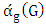 and
and 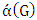 .Lemma 6. If
.Lemma 6. If  is an isolate-free bipartite graph, then each partite set contains a liberal vertex.Proof.Color red all edges of
is an isolate-free bipartite graph, then each partite set contains a liberal vertex.Proof.Color red all edges of  that belong to no maximum matching. Let
that belong to no maximum matching. Let  be a fixed maximum matching of
be a fixed maximum matching of  , and color blue all edges of
, and color blue all edges of 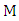 . Thus, each vertex of
. Thus, each vertex of 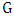 is incident with at most one blue edge.Let us say a path is happy if the edges alternate colors. Let
is incident with at most one blue edge.Let us say a path is happy if the edges alternate colors. Let 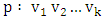 be a longest happy path in
be a longest happy path in 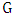 . As in the proof of Lemma 5, an
. As in the proof of Lemma 5, an 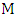 -un matched vertex is not incident with any red edge. So if the first edge of
-un matched vertex is not incident with any red edge. So if the first edge of 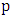 is red, vertex
is red, vertex 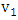 must be incident with a blue edge; by the maximality of
must be incident with a blue edge; by the maximality of 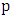 , this blue edge must join
, this blue edge must join 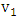 to a vertex of
to a vertex of 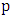 ; indeed, this blue edge must join
; indeed, this blue edge must join 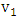 to
to 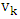 , since all other vertices of
, since all other vertices of 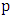 are already incident with a blue edge. But then, if we take
are already incident with a blue edge. But then, if we take 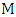 and remove the (blue) edges of
and remove the (blue) edges of 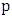 and add the red edges of
and add the red edges of 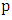 , we get another maximum matching, contradicting the claim that the edges are red. It follows that both the first and last edge of the happy path
, we get another maximum matching, contradicting the claim that the edges are red. It follows that both the first and last edge of the happy path 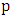 are colored blue. In particular this implies that
are colored blue. In particular this implies that 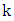 is even.Suppose that
is even.Suppose that 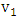 is not liberal. That is, it is incident with at least one red edge. It follows by the maximality of
is not liberal. That is, it is incident with at least one red edge. It follows by the maximality of 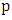 that
that 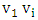 is a red edge for some
is a red edge for some 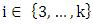 . Since
. Since 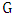 is bipartite, the cycle
is bipartite, the cycle 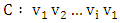 is an even cycle whose edges alternate between blue and red edges. Replacing the (blue) edges of
is an even cycle whose edges alternate between blue and red edges. Replacing the (blue) edges of 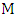 that belong to
that belong to 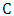 with the (red) edges of
with the (red) edges of 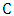 not in
not in 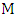 and leaving all other edges of
and leaving all other edges of 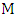 unchanged, produces a new maximum matching of
unchanged, produces a new maximum matching of 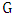 that contains some red edges, contradicting the definition of a red edge [10].And by this we have proven the vertex
that contains some red edges, contradicting the definition of a red edge [10].And by this we have proven the vertex 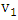 is liberal and in the same way we prove that
is liberal and in the same way we prove that 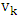 is liberal, then every partite sets have liberal vertex.Theorem 2. If
is liberal, then every partite sets have liberal vertex.Theorem 2. If  is a bipartite graph, then
is a bipartite graph, then 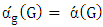 .Proof.It is produced from Lemmas 4 and 6 [10].An example of this, in the following figure we have
.Proof.It is produced from Lemmas 4 and 6 [10].An example of this, in the following figure we have 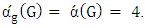
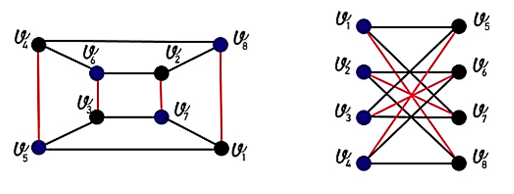 | Figure 5. Example of bipartite graph has 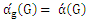 |
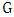 is a complete multipartite graph, then
is a complete multipartite graph, then 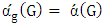 .Proof. Assume
.Proof. Assume 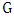 is a complete multipartite graph with partite sets
is a complete multipartite graph with partite sets  where
where 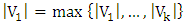 . By Lemma 4 it is sufficient to show that if
. By Lemma 4 it is sufficient to show that if 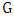 is nonempty then it contains a liberal vertex. By Lemma 5 we may assume that
is nonempty then it contains a liberal vertex. By Lemma 5 we may assume that 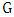 has a perfect matching, say
has a perfect matching, say 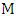 . We claim that every vertex
. We claim that every vertex 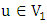 is liberal. For, suppose there is an edge
is liberal. For, suppose there is an edge 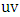 incident with
incident with 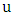 that is not in any perfect matching; say
that is not in any perfect matching; say 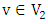 . By symmetry, no edge between
. By symmetry, no edge between 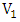 and
and 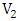 is in a perfect matching. Since
is in a perfect matching. Since 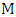 is perfect, it contains edges incident with
is perfect, it contains edges incident with 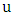 and
and 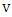 ; say
; say 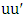 and
and 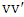 . If
. If 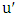 and
and 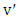 are adjacent, then
are adjacent, then 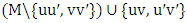 is a perfect matching that contains the edge
is a perfect matching that contains the edge 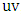 , a contradiction. So, assume that
, a contradiction. So, assume that 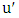 and
and 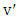 are in the same partite set, say
are in the same partite set, say 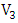 (as observed earlier,
(as observed earlier, 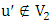 and
and 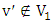 ).Since
).Since 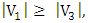 there is a vertex,
there is a vertex,  say, in
say, in  that is not
that is not  -matched to a vertex of
-matched to a vertex of 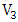 . Hence, the vertex
. Hence, the vertex 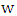 is incident with an edge of
is incident with an edge of 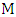 , say
, say 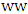 , where
, where 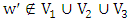 . But then
. But then 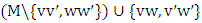 is a perfect matching that contains the edge
is a perfect matching that contains the edge 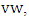 a contradiction. Thus, every vertex of
a contradiction. Thus, every vertex of 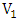 is liberal [10].An example of this, in the following figure the complete multipartite graph
is liberal [10].An example of this, in the following figure the complete multipartite graph 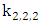 we have
we have 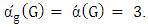
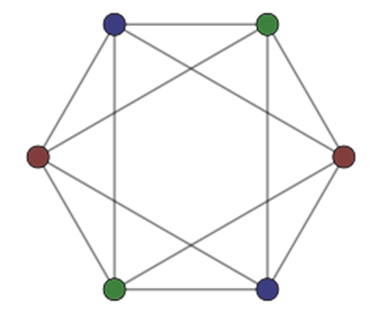 | Figure 6. Complete multipartite graph 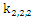 |
4. Lower Bounds
- We next consider lower bounds for the matcher game, especially in relation to the matching and lower matching numbers. We will need the following lemma.Lemma 7.If
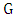 is a graph and
is a graph and 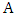 is an independent set of vertices such that there is a matching that covers
is an independent set of vertices such that there is a matching that covers 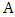 , then
, then 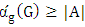 .Proof. Let
.Proof. Let 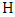 be the bipartite subgraph of
be the bipartite subgraph of 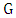 with vertex set
with vertex set 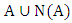 and edge-set the edges incident with
and edge-set the edges incident with 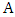 . By Lemma 6 there is a vertex
. By Lemma 6 there is a vertex 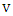 of
of 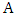 that is liberal in
that is liberal in 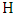 . Maximizer chooses this vertex. Say Minimizer chooses
. Maximizer chooses this vertex. Say Minimizer chooses 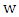 in response. Since
in response. Since 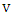 is liberal in
is liberal in 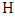 , the edge
, the edge 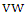 is in a maximum matching
is in a maximum matching 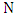 of
of 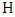 . The matching
. The matching 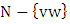 covers
covers 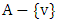 in
in 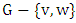 . Thus the result follows by induction. For example, the above lemma shows that if a graph
. Thus the result follows by induction. For example, the above lemma shows that if a graph 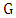 has a perfect matching, then
has a perfect matching, then 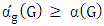 , here
, here 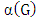 is the independence number of
is the independence number of 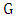 . We next use the above lemma to provide a lower bound on the matcher number in terms of the lower matching number.Lemma 8. If
. We next use the above lemma to provide a lower bound on the matcher number in terms of the lower matching number.Lemma 8. If 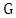 is a graph, then
is a graph, then 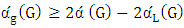 .Proof.Consider a maximum matching
.Proof.Consider a maximum matching 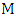 and a minimum maximal matching
and a minimum maximal matching 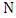 . Then the vertices of
. Then the vertices of 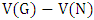 form an independent set. Further, at most
form an independent set. Further, at most 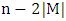 of them are not covered by
of them are not covered by 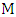 , where
, where 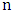 is the order of
is the order of 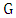 . That is, there is a subset of
. That is, there is a subset of 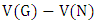 of at least
of at least 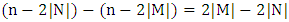 vertices, all of whose vertices are
vertices, all of whose vertices are 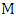 -matched. By Lemma 7, it follows that
-matched. By Lemma 7, it follows that 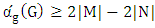 .For example, if the lower matching number is half the matching number, then the matcher and matching numbers are equal.As another consequence of Lemma 8 and the earlier trivial observation that
.For example, if the lower matching number is half the matching number, then the matcher and matching numbers are equal.As another consequence of Lemma 8 and the earlier trivial observation that 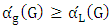 , we obtain the following lower bound:Theorem 4.If
, we obtain the following lower bound:Theorem 4.If 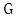 is a graph then
is a graph then 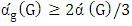 .Proof.
.Proof. 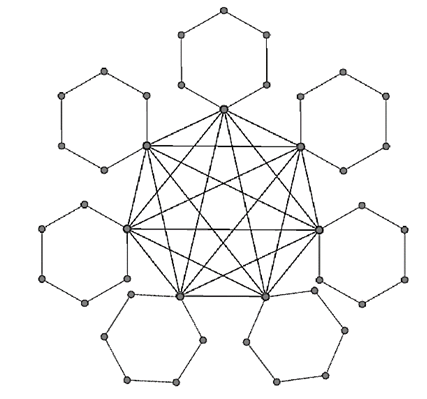 | Figure 7. Depiction of  |
 , the edge played by Min in response is incident to at most two edges of a maximum matching and hence reduces the matching number (of the residual graph) by at most 2. Hence a round reduces
, the edge played by Min in response is incident to at most two edges of a maximum matching and hence reduces the matching number (of the residual graph) by at most 2. Hence a round reduces  by at most 3 while adding2 to the number of edges played. When
by at most 3 while adding2 to the number of edges played. When 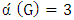 and Max starts, two more edges will be played.For graph
and Max starts, two more edges will be played.For graph 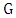 and integer
and integer 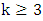 , define the generalized corona
, define the generalized corona 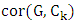 as follows. For each vertex
as follows. For each vertex 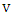 of
of 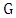 introduce a disjoint k-cycle and identify one vertex of the cycle with
introduce a disjoint k-cycle and identify one vertex of the cycle with 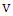 ; we call the vertex
; we call the vertex 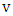 the root of the cycle. For example, here is a depiction of
the root of the cycle. For example, here is a depiction of 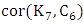 .Lemma 9. If graph
.Lemma 9. If graph 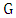 has order
has order 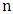 and
and 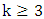 is odd, then
is odd, then 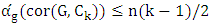 .Proof. In each copy of
.Proof. In each copy of 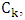 color red both edges incident with the root and then every alternate edge. Note that every root is incident with exactly two red edges and every other vertex is incident with exactly one red edge. The strategy for Minimizer is to prefer red edges. That is, if possible, she chooses a neighbor connected by a red edge to Maximizer’s choice, otherwise she chooses any neighbor.We claim that Minimizer’s strategy means that every root will be matched to a vertex inside its copy of
color red both edges incident with the root and then every alternate edge. Note that every root is incident with exactly two red edges and every other vertex is incident with exactly one red edge. The strategy for Minimizer is to prefer red edges. That is, if possible, she chooses a neighbor connected by a red edge to Maximizer’s choice, otherwise she chooses any neighbor.We claim that Minimizer’s strategy means that every root will be matched to a vertex inside its copy of 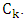 Focus on some copy
Focus on some copy 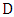 , and let
, and let 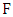 be the set consisting of the root and its two neighbors in
be the set consisting of the root and its two neighbors in 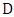 . The strategy for Minimizer means that if Maximizer chooses a vertex in
. The strategy for Minimizer means that if Maximizer chooses a vertex in 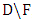 , then so does Minimizer. Thus, Maximizer must be the first to choose a vertex in
, then so does Minimizer. Thus, Maximizer must be the first to choose a vertex in 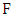 ; and when he does so, Minimizer chooses its neighbor in
; and when he does so, Minimizer chooses its neighbor in 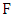 . Thus the root is matched within
. Thus the root is matched within 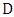 .It follows that at the end of the game, at least one vertex from each copy of
.It follows that at the end of the game, at least one vertex from each copy of 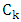 is unmatched. That is, the maximal matching obtained has size at most
is unmatched. That is, the maximal matching obtained has size at most 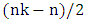 .It follows that
.It follows that 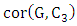 is an example of equality in Theorem 4 whenever
is an example of equality in Theorem 4 whenever 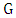 has a perfect matching.
has a perfect matching.4.1. Odd Girth
- We now consider a generalization of Theorem 4. Recall that the odd-girth of a nonbipartite graph
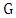 is the shortest length of an odd cycle in
is the shortest length of an odd cycle in 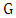 .Theorem 5. If graph
.Theorem 5. If graph 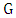 has odd girth g, then
has odd girth g, then 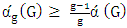 .Proof. The proof is by induction on the order. If there is an isolated vertex, then we can just discard it and induct; so, assume that
.Proof. The proof is by induction on the order. If there is an isolated vertex, then we can just discard it and induct; so, assume that 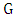 is isolated-free. If there is a liberal vertex
is isolated-free. If there is a liberal vertex 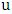 in
in 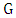 , then Maximizer chooses that vertex and we induct after Minimizer’s response. So, we may assume there is no liberal vertex. In particular, by Lemma 5, the graph has a perfect matching, say
, then Maximizer chooses that vertex and we induct after Minimizer’s response. So, we may assume there is no liberal vertex. In particular, by Lemma 5, the graph has a perfect matching, say 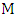 .As usual we color red each edge that is in no perfect matching.Say Maximizer starts with vertex
.As usual we color red each edge that is in no perfect matching.Say Maximizer starts with vertex 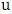 and Minimizer responds with vertex
and Minimizer responds with vertex 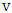 . If the edge
. If the edge 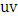 is in some perfect matching, then again, we can just induct on
is in some perfect matching, then again, we can just induct on 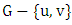 . So we may assume that the edge
. So we may assume that the edge 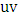 is red. Let
is red. Let 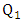 be the path
be the path 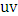 . Now the initial strategy of Maximizer will be to do the following as long as it is possible:choose the
. Now the initial strategy of Maximizer will be to do the following as long as it is possible:choose the 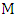 -partner of one end of the current path,where by
-partner of one end of the current path,where by 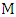 -partner of vertex
-partner of vertex 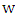 we mean the vertex
we mean the vertex 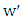 such that
such that 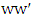 is in
is in  . So, we obtain a series of
. So, we obtain a series of  -alternating paths
-alternating paths 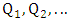 such that each
such that each 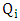 has
has 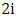 vertices and starts and finishes with an edge not in M.If such a choice were always valid, then Maximizer would match off the entire graph, a contradiction of the fact that
vertices and starts and finishes with an edge not in M.If such a choice were always valid, then Maximizer would match off the entire graph, a contradiction of the fact that 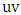 is red. So, Maximizer becomes stuck somewhere; that is, he cannot choose the
is red. So, Maximizer becomes stuck somewhere; that is, he cannot choose the 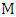 -partner of either end of the current path since neither has an unchosen neighbor. Say we have path
-partner of either end of the current path since neither has an unchosen neighbor. Say we have path 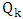 with ends
with ends 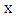 and
and 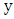 . Let
. Let 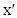 be the
be the 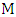 -partner of
-partner of 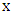 and
and 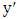 the
the 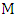 -partner of
-partner of 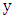 . Since Maximizer is stuck, all neighbors of
. Since Maximizer is stuck, all neighbors of 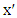 and
and 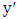 are on
are on 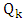 .Suppose that
.Suppose that 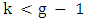 . By assumption, vertex
. By assumption, vertex 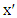 is not liberal and so is incident to a red edge, say
is not liberal and so is incident to a red edge, say 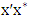 . If the edge
. If the edge 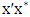 creates an even cycle with the path
creates an even cycle with the path 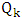 , then we have a contradiction, since every edge in such an
, then we have a contradiction, since every edge in such an 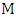 -alternating cycle is in a perfect matching. So, the edge
-alternating cycle is in a perfect matching. So, the edge 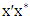 must create an odd cycle with
must create an odd cycle with 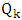 . Similarly,
. Similarly, 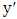 is joined by a red edge to some vertex
is joined by a red edge to some vertex 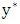 on
on 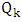 . that creates an odd cycle. By the odd-girth condition,
. that creates an odd cycle. By the odd-girth condition, 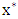 is closer to
is closer to 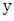 than
than 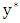 is along the path
is along the path 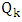 . See figure.
. See figure.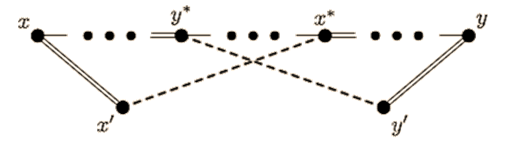 | Figure 8. -alternating cycle formed by 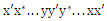 |
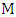 -alternating cycle formed by
-alternating cycle formed by 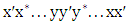 . It follows that the edge
. It follows that the edge 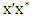 is in a perfect matching, a contradiction of the claim that it is red.That is, it must be the case that
is in a perfect matching, a contradiction of the claim that it is red.That is, it must be the case that 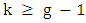 . Then the remaining graph
. Then the remaining graph 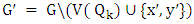 has a perfect matching, and we can apply induction to
has a perfect matching, and we can apply induction to 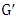 . The final matching is the union of a matching that has size
. The final matching is the union of a matching that has size 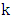 from
from 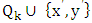 and a matching that has size at least
and a matching that has size at least 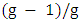 of
of 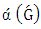 . The lower bound follows since
. The lower bound follows since 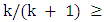
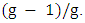 Note that for
Note that for 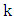 odd, the generalized corona
odd, the generalized corona 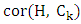 has a perfect matching if and only if the graph
has a perfect matching if and only if the graph 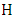 has a perfect matching. By Lemma 9, it follows that
has a perfect matching. By Lemma 9, it follows that 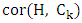 is an example of equality in Theorem 5 for all odd
is an example of equality in Theorem 5 for all odd  and graphs
and graphs 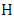 with a perfect matching and girth at least
with a perfect matching and girth at least 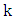 .Using the ideas in the above proof, one can characterize the graphs that achieve equality in Theorem 4.Theorem 6. If
.Using the ideas in the above proof, one can characterize the graphs that achieve equality in Theorem 4.Theorem 6. If 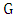 is an isolate-free graph, then
is an isolate-free graph, then 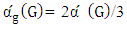 if and only if it is isomorphic to
if and only if it is isomorphic to  for some graph with a perfect matching.Proof. Suppose that
for some graph with a perfect matching.Proof. Suppose that 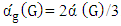 . Consider the proof of Theorem 5 for the case that
. Consider the proof of Theorem 5 for the case that 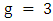 . To obtain equality, it is necessary that every vertex is incident with a red edge and that there is a perfect matching
. To obtain equality, it is necessary that every vertex is incident with a red edge and that there is a perfect matching  . Further, in applying hisstrategy, Maximizer must get stuck with
. Further, in applying hisstrategy, Maximizer must get stuck with 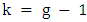 . So we have an alternating path
. So we have an alternating path  with 4 vertices. Let B denote the subgraph induced by
with 4 vertices. Let B denote the subgraph induced by  . See figure.
. See figure.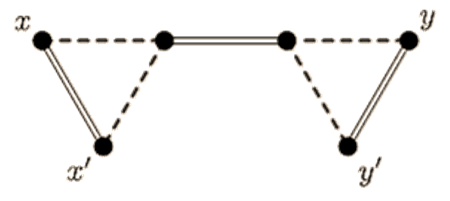 | Figure 9. Alternating path  with 4 vertices with 4 vertices |
 and
and 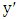 have degree 2. Since Maximizer can start with any vertex, it follows that every vertex has a neighbor of degree 2. In particular, the degree-2 vertices come in pairs.For equality, one needs that the graph
have degree 2. Since Maximizer can start with any vertex, it follows that every vertex has a neighbor of degree 2. In particular, the degree-2 vertices come in pairs.For equality, one needs that the graph 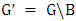 is also an example of equality. By induction, the graph
is also an example of equality. By induction, the graph 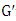 is isomorphic to
is isomorphic to 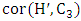 where
where 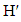 is a graph with a perfect matching. Since the degree-2 vertices form a paired dominating set, it follows that in
is a graph with a perfect matching. Since the degree-2 vertices form a paired dominating set, it follows that in 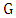 the only edges between B and
the only edges between B and 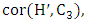 if any, are between the vertices that already have degree at least 3 in that subgraph. Thus, the original graph
if any, are between the vertices that already have degree at least 3 in that subgraph. Thus, the original graph 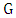 has the desired structure. In general, it seems likely that the only graphs that achieve equality in Theorem 5 are the ones already noted; that is,
has the desired structure. In general, it seems likely that the only graphs that achieve equality in Theorem 5 are the ones already noted; that is, 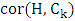 for
for 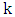 odd and
odd and 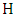 a graph with a perfect matching and girth at least
a graph with a perfect matching and girth at least 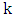 . As in the proof of Theorem 6, one can readily show that graphs with equality in Theorem 5 have
. As in the proof of Theorem 6, one can readily show that graphs with equality in Theorem 5 have 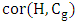 as a spanning subgraph, and by the odd-girth condition, the copies of
as a spanning subgraph, and by the odd-girth condition, the copies of 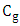 are induced. What seems harder to resolve is the absence or existence of other edges between the cycles.
are induced. What seems harder to resolve is the absence or existence of other edges between the cycles.5. Dense Graphs
- We consider some dense graphs and show that their matcher number is half their order. It is well-known that if the minimum degree is at least half the order, and the order is even, then the graph has a perfect matching. (For example, this follows from Dirac’s theorem [12].)It follows from Theorem 3 that graphs of even order with minimum degree at least
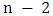 have matcher number
have matcher number 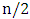 .(Since such minimum degree implies the graph is complete multipartite.) Here is a tiny improvement on this.Lemma 10. If graph
.(Since such minimum degree implies the graph is complete multipartite.) Here is a tiny improvement on this.Lemma 10. If graph 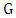 has even order
has even order 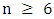 and minimum degree
and minimum degree 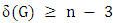 , then
, then 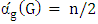 .Proof. The strategy for Maximizer is simply to choose any vertex of minimum degree.Consider the situation when four vertices remain. The current graph, say
.Proof. The strategy for Maximizer is simply to choose any vertex of minimum degree.Consider the situation when four vertices remain. The current graph, say 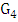 , has minimum degree at least 1. Suppose it does not have a perfect matching. Then
, has minimum degree at least 1. Suppose it does not have a perfect matching. Then 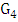 is (isomorphic to) the star with three edges. Let
is (isomorphic to) the star with three edges. Let 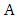 denote the set of the three end-vertices in
denote the set of the three end-vertices in 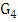 . Now, go back to the graph, say
. Now, go back to the graph, say 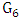 , with six vertices remaining. That graph
, with six vertices remaining. That graph 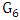 has minimum degree at least 3. So all three vertices of
has minimum degree at least 3. So all three vertices of  are adjacent in
are adjacent in 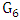 to the two vertices matched in
to the two vertices matched in  ; this means that in
; this means that in  each vertex in
each vertex in  has degree 3 while the vertices matched each have degree at least 4. This is a contradiction of Maximizer’s strategy.Thus, it follows that
has degree 3 while the vertices matched each have degree at least 4. This is a contradiction of Maximizer’s strategy.Thus, it follows that 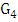 has a perfect matching. It is easily checked that the strategy of choosing a vertex of minimum degree ensures that the resultant maximal matching is perfect.One can improve the above lemma slightly. Computer search shows that all graphs of order 8 and minimum degree at least 4 have matcher number 4. It follows that if graph
has a perfect matching. It is easily checked that the strategy of choosing a vertex of minimum degree ensures that the resultant maximal matching is perfect.One can improve the above lemma slightly. Computer search shows that all graphs of order 8 and minimum degree at least 4 have matcher number 4. It follows that if graph 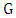 has even order
has even order 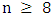 and minimum degree at least
and minimum degree at least 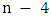 , then the matcher number is
, then the matcher number is 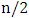 . (Maximizer plays arbitrarily until eight vertices remain, and then uses the optimal strategy.)Lemma 11. If two graphs have the same order m, then the matcher number of their join is
. (Maximizer plays arbitrarily until eight vertices remain, and then uses the optimal strategy.)Lemma 11. If two graphs have the same order m, then the matcher number of their join is 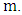 Proof. The vertex set of the join can be partitioned into sets
Proof. The vertex set of the join can be partitioned into sets 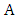 and
and 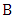 of size m such that every edge between
of size m such that every edge between 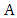 and
and 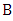 is present. If both
is present. If both 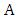 and
and 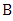 are independent sets, then the graph is
are independent sets, then the graph is 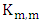 and we are done. So, assume there is some edge
and we are done. So, assume there is some edge 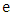 with both ends in
with both ends in 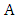 .Then Maximizer starts by choosing any vertex in
.Then Maximizer starts by choosing any vertex in 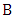 . If Minimizer takes a vertex of
. If Minimizer takes a vertex of 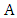 , then the result follows by induction (as the remaining graph is the join of two graphs of order
, then the result follows by induction (as the remaining graph is the join of two graphs of order 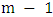 ). So, assume that she chooses a vertex of
). So, assume that she chooses a vertex of 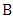 .If only two vertices of
.If only two vertices of 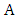 remain, then we are done, since they are joined by edge
remain, then we are done, since they are joined by edge 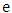 and every other vertex has been matched. So, assume more than two vertices remain in
and every other vertex has been matched. So, assume more than two vertices remain in 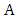 . Then Maximizer chooses a vertex in
. Then Maximizer chooses a vertex in 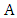 but avoiding both ends of
but avoiding both ends of 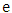 . If Minimizer chooses a vertex in
. If Minimizer chooses a vertex in 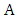 , we are back to having equal number of vertices in the two sets, and so can induct.So, assume that she chooses a vertex of
, we are back to having equal number of vertices in the two sets, and so can induct.So, assume that she chooses a vertex of 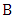 . But then Maximizer chooses another vertex in
. But then Maximizer chooses another vertex in 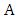 , avoiding the ends of e, and the argument repeats.
, avoiding the ends of e, and the argument repeats.6. Conclusions
- We provided bounds on the matcher games. It seems that the Max-start matcher game might be interesting for special families of graphs. For example, rooks' graphs or cartesian products in general seem worthy of consideration, as do cubic graphs or chordal graphs. In another direction, a natural question is the complexity of the game.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML