-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2020; 10(2): 33-37
doi:10.5923/j.ajms.20201002.01

Bipolar Fuzzy α-ideal of BP-algebra
Osama Rashad El-Gendy
Batterjee Medical College for Sciences & Technology, Jeddah, Saudi Arabia
Correspondence to: Osama Rashad El-Gendy, Batterjee Medical College for Sciences & Technology, Jeddah, Saudi Arabia.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, the concept of bipolar fuzzy α-ideal of BP-algebra is introduced. We introduced α-ideal and fuzzy α-ideal. Several theorems are presented in this regard. The homomorphic image and inverse image of the bipolar fuzzy α-ideal are studied.
Keywords: BP-algebra, α-ideal, fuzzy α-ideal, Bipolar fuzzy -ideal
Cite this paper: Osama Rashad El-Gendy, Bipolar Fuzzy α-ideal of BP-algebra, American Journal of Mathematics and Statistics, Vol. 10 No. 2, 2020, pp. 33-37. doi: 10.5923/j.ajms.20201002.01.
Article Outline
1. Introduction
- Y. Imai and K. Iséki introduced two classes of abstract algebras: BCK-algebras and BCI-algebras [7,8]. It is known that the class of BCK-algebras is a proper subclass of the class of BCI-algebras. In [4,5], Q. P. Hu and X. Li introduced a wide class of abstract: BCH-algebras. They had shown that the class of BCI-algebras is a proper subclass of the class of BCH-algebras. In [27], J. Neggers, S. S. Ahn and H. S. Kim introduced Q-algebras which is a generalization of BCK / BCI-algebras and obtained several results. In 2002, Neggers and Kim [19,26,28] introduced a new notion, called a B-algebra, and obtained several results. In 2007, Walendziak [30] introduced a new notion, called a BF-algebra, which is a generalization of B-algebra. In 2013, Ahn and Han. [2] introduced a new notion, called BP-algebra which is related to several classes of algebra. In 1965, the concept of fuzzy sets, a remarkable idea in mathematics, was proposed by Zadeh [31]. In this traditional concept of fuzzy set, the membership degree expresses belongingness of an element to a fuzzy set. The membership degree of an element ranges over the interval [0, 1]. When the membership degree of an element is 1, then the element completely belongs to its corresponding fuzzy set, and the membership degree of an element is 0 means an element does not belong to the fuzzy set. Based on this tool, different fuzzy algebraic structures have been developed by many researchers, The fuzzy structures of BCK/BCI-algebras worked out by many researchers such as Jun [16,17,18,25], Liu [24], Bej and Pal [3], Jana et al. and others [10-15] have done much investigations on BCK/BCI/G/B-algebras related to these algebras. In 1994, the notion of bipolar fuzzy sets was proposed by Zhang [32,33] as a generalization of fuzzy sets [31]. Bipolar-valued fuzzy sets [22,23] are seen as an extension of fuzzy sets whose membership degree range is enlarged from the interval [0, 1] to [−1, 1]. In a bipolar fuzzy set, the membership degree 0 of an element means that the element is irrelevant to the corresponding property, the membership degree (0, 1] of an element indicates that the element somewhat satisfies the property, and the membership degree [−1, 0) of an element indicates that the element somewhat satisfies the implicit counter-property. Bipolar fuzzy sets have various applications in fuzzy algebras. For example, bipolar fuzzy ideals [1] in LA-semigroups, bipolar fuzzy sub-algebras and ideals [21] of BCK/BCI-algebras, bipolar fuzzy a-ideals in BCK/BCI-algebras [20] and bipolar valued fuzzy BCK/BCI-algebras [29] are some of them. The aim of this paper is to apply the notion of the bipolar fuzzy set to α-ideal of BP-algebra. The notions of α-ideal, fuzzy α-ideal and bipolar fuzzy α-ideal are defined, and a lot of properties are investigated. The homomorphic image and the inverse image of the bipolar fuzzy α-ideal are studied. Several theorems and basic properties that are related to the bipolar fuzzy α-ideal of BP-algebra are investigated. In section 5, we conclude and present some topics for future research.
2. Preliminaries
- In this section, some elementary aspects necessary for this paper are included.Definition 2.1 [2]. An algebra
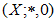 is called BP-algebra if it satisfies the following axioms:
is called BP-algebra if it satisfies the following axioms: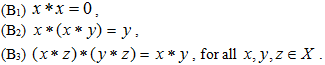 In X, we can define a binary relation “≤” by x ≤ y if and only if
In X, we can define a binary relation “≤” by x ≤ y if and only if 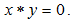 Example 2.2 [2]. Let
Example 2.2 [2]. Let 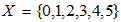 . Define
. Define 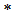 on
on 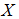 as the following table:
as the following table: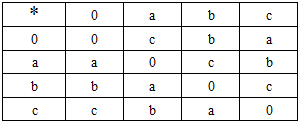 Then
Then 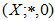 is a BP-algebra.Theorem 2.3 [2]. If
is a BP-algebra.Theorem 2.3 [2]. If 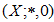 is a BP-algebra, then following conditions hold: for any
is a BP-algebra, then following conditions hold: for any 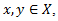
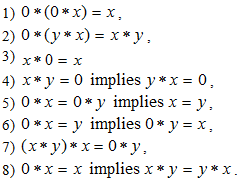 Example 2.4 [2]. Let
Example 2.4 [2]. Let 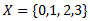 Define
Define 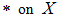 as the following table:
as the following table: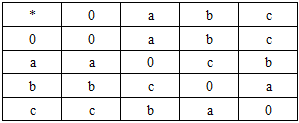 Then
Then 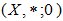 is a BP-algebra
is a BP-algebra3. α-ideal & Fuzzy α-ideal of BP-algebra
- In this section,
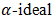 and fuzzy
and fuzzy 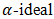 of BP-algebra are defined and some important properties are presented.Definition 3.1. A nonempty subset S of a BP-algebra X is called a subalgebra of X if
of BP-algebra are defined and some important properties are presented.Definition 3.1. A nonempty subset S of a BP-algebra X is called a subalgebra of X if 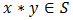 for all
for all 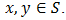 Definition 3.2. A non-empty subset
Definition 3.2. A non-empty subset 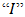 of a BP-algebra
of a BP-algebra 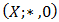 is called a
is called a 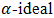 if for all
if for all 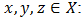
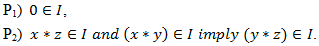 Definition 3.3. Let
Definition 3.3. Let 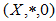 and
and 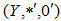 be BP-algebra. A mapping
be BP-algebra. A mapping 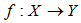 is said to be a homomorphism if
is said to be a homomorphism if 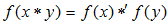 , for all
, for all 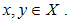 Definition 3.4. Let
Definition 3.4. Let 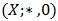 be a BP-algebra. A fuzzy set
be a BP-algebra. A fuzzy set 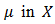 is called a fuzzy
is called a fuzzy 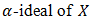 if it satisfies:
if it satisfies: 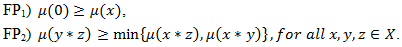 Example 3.5. Consider a BP-algebra X = {0, a, b, c} in which the
Example 3.5. Consider a BP-algebra X = {0, a, b, c} in which the  operation is given by example 2.4. Let
operation is given by example 2.4. Let 
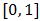 be such that
be such that 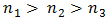 . Define the mapping
. Define the mapping 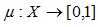 by
by 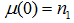 ,
, 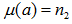 and
and 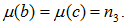 Then routine calculations give that
Then routine calculations give that 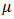 is a fuzzy
is a fuzzy 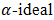 of X.Proposition 3.6. If
of X.Proposition 3.6. If 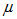 is a fuzzy α-ideal of BP-algebra X, then
is a fuzzy α-ideal of BP-algebra X, then 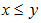 implies
implies 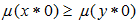 , for all
, for all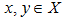 .Proof. Let
.Proof. Let 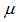 be a Fuzzy
be a Fuzzy 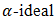 of BP-algebra X.By definition 2.1, if
of BP-algebra X.By definition 2.1, if 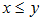 then
then 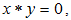 and
and 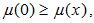 given that
given that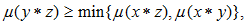 for all
for all 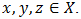 Then
Then 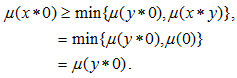
4. Bipolar Fuzzy α-ideal of BP-algebra
- In this section, we defined bipolar fuzzy
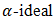 of BP-algebra and examined some related properties.Definition 4.1 [22]. A bipolar fuzzy set
of BP-algebra and examined some related properties.Definition 4.1 [22]. A bipolar fuzzy set 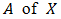 is defined as
is defined as 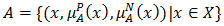 where
where 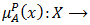
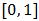 and
and 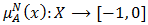 are mappings. The positive membership degree
are mappings. The positive membership degree 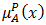 denotes the satisfaction degree of an element
denotes the satisfaction degree of an element 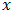 to the property corresponding to a bipolar fuzzy set
to the property corresponding to a bipolar fuzzy set 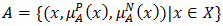 and the negative membership degree
and the negative membership degree 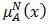 denotes the satisfaction degree of an element
denotes the satisfaction degree of an element 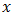 to some implicit counter property of
to some implicit counter property of 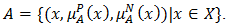 If
If 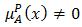 and
and  this case is regarded as having only a positive satisfaction degree for
this case is regarded as having only a positive satisfaction degree for 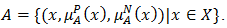 If
If 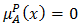 and
and 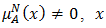 does not satisfy the property of
does not satisfy the property of 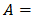
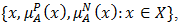 but somewhat satisfies the counter property of
but somewhat satisfies the counter property of 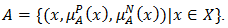 In some cases, it is possible for an element
In some cases, it is possible for an element 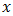 to be
to be 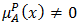 and
and 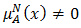 when the membership function of the property overlaps that of the counter property of its portion of the domain (Lee [26]). We shall use the symbol
when the membership function of the property overlaps that of the counter property of its portion of the domain (Lee [26]). We shall use the symbol 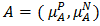 for the bipolar fuzzy set
for the bipolar fuzzy set 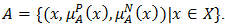 Definition 4.2 [32]. For every two bipolar fuzzy set
Definition 4.2 [32]. For every two bipolar fuzzy set 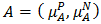 and
and 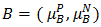 in
in 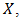 we define
we define 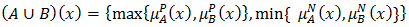
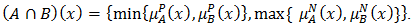 Proposition 4.3 [21]. A bipolar fuzzy set
Proposition 4.3 [21]. A bipolar fuzzy set 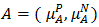 of
of 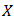 is called a bipolar fuzzy subalgebra of
is called a bipolar fuzzy subalgebra of 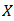 if it satisfies
if it satisfies 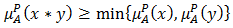 and
and 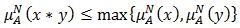 for all
for all 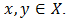 Definition 4.4 [21]. A bipolar fuzzy set
Definition 4.4 [21]. A bipolar fuzzy set 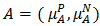 of
of 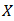 is called a bipolar fuzzy ideal of
is called a bipolar fuzzy ideal of 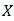 if it satisfies the following conditions
if it satisfies the following conditions 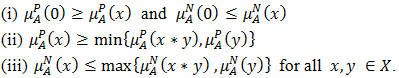 Definition 4.5. A bipolar fuzzy set
Definition 4.5. A bipolar fuzzy set 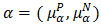 of a BP-algebra
of a BP-algebra 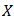 is called a bipolar fuzzy
is called a bipolar fuzzy 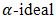 of
of 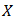 if it satisfies the following conditions
if it satisfies the following conditions 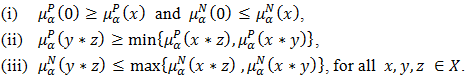 Example 4.6. Consider a BP-algebra X = {0, a, b, c} in which the
Example 4.6. Consider a BP-algebra X = {0, a, b, c} in which the  operation is given by example 2.4. Define a bipolar fuzzy set
operation is given by example 2.4. Define a bipolar fuzzy set  by,
by,  and
and  routine calculation gives that
routine calculation gives that  is a bipolar fuzzy
is a bipolar fuzzy 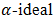 of
of 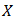 .Theorem 4.7. The intersection of any set of bipolar fuzzy
.Theorem 4.7. The intersection of any set of bipolar fuzzy 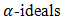 in BP-algebra
in BP-algebra 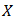 is also a bipolar fuzzy
is also a bipolar fuzzy 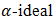 of
of 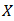 . Proof. Let
. Proof. Let 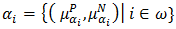 be a family of bipolar fuzzy
be a family of bipolar fuzzy 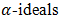 in BP-algebra
in BP-algebra 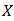 . Then for any
. Then for any 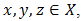
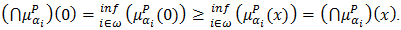 And
And 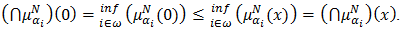
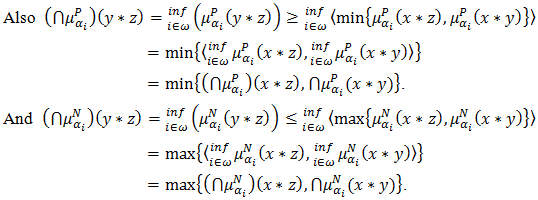 Proposition 4.8. Let
Proposition 4.8. Let 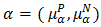 be a bipolar fuzzy
be a bipolar fuzzy 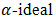 of BP-algebra. If
of BP-algebra. If 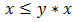 holds in
holds in 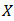 , then
, then 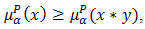 and
and 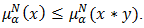 Proof. Let
Proof. Let 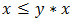 holds in
holds in 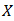 . Then
. Then 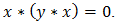 Since
Since 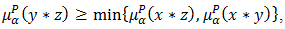 and
and 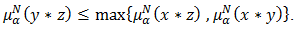 Then
Then 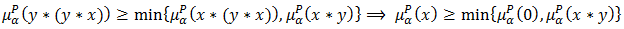
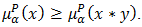 And
And 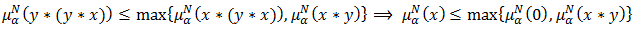
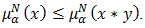 Proposition 4.9. Let
Proposition 4.9. Let 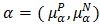 be a bipolar fuzzy
be a bipolar fuzzy 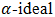 of BP-algebra
of BP-algebra 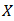 . If
. If 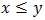 holds in
holds in 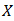 , then
, then 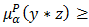
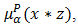 and
and 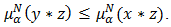 Proof. Let
Proof. Let 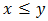 holds in
holds in 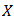 . Then
. Then 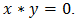 Since
Since 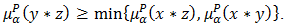 Then
Then 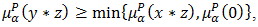
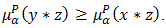 And
And 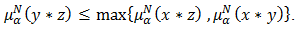 Then
Then 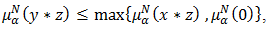
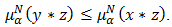 Definition 4.10. Let
Definition 4.10. Let 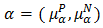 be a bipolar fuzzy
be a bipolar fuzzy 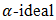 of BP-algebra
of BP-algebra 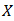 and
and 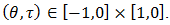 We define
We define 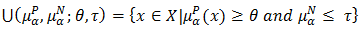 is called upper
is called upper 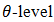 cut of
cut of 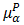 and lower
and lower 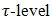 cut of
cut of 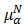 of the bipolar fuzzy
of the bipolar fuzzy 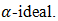 Theorem 4.11. Let
Theorem 4.11. Let 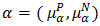 be a bipolar fuzzy
be a bipolar fuzzy 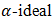 of BP-algebra
of BP-algebra 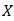 . Then for every
. Then for every 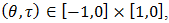
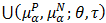 is
is 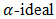 of BP-algebra.Proof. Assume that
of BP-algebra.Proof. Assume that 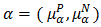 is a bipolar fuzzy
is a bipolar fuzzy 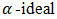 of
of 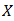 . For
. For 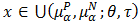 so
so 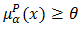 and
and 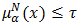 where
where 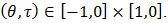 Now we get that
Now we get that 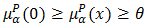 and
and 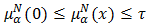 this implies that
this implies that 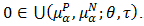 Next, let
Next, let 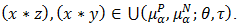 This means
This means 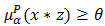 and
and 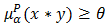 also,
also, 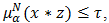 and
and 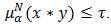 Then
Then 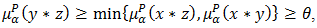 and
and 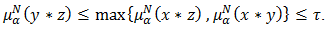 This implies that
This implies that 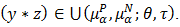 Hence
Hence 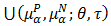 is a
is a 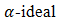 of BP-algebra.Definition 4.12. Let
of BP-algebra.Definition 4.12. Let  and
and 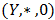 be BP-algebras, and let
be BP-algebras, and let 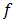 be a mapping from the set
be a mapping from the set 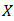 and the set
and the set 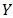 . If
. If 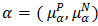 and
and 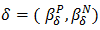 are bipolar fuzzy sets of
are bipolar fuzzy sets of 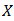 and
and 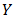 respectively. Then
respectively. Then 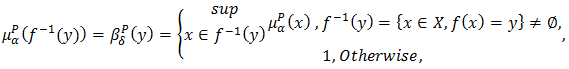 And
And 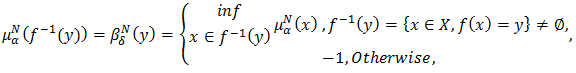 For all
For all 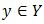 is called the image of
is called the image of 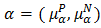 under
under 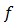 . Similarly, the inverse image
. Similarly, the inverse image 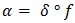 in
in 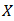 defined as,
defined as, 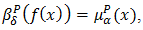 and
and 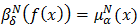 for all
for all 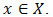 Theorem 4.13. An into homomorphic inverse image of a bipolar fuzzy
Theorem 4.13. An into homomorphic inverse image of a bipolar fuzzy 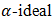 of BP-algebra is also bipolar fuzzy
of BP-algebra is also bipolar fuzzy 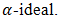 Proof. Let
Proof. Let 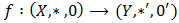 be an into homomorphism of BP-algebras. Assume that
be an into homomorphism of BP-algebras. Assume that 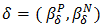 is a bipolar fuzzy
is a bipolar fuzzy 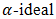 in
in 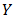 , and
, and 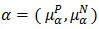 is a bipolar fuzzy
is a bipolar fuzzy 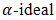 in
in 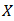 . Then for all
. Then for all 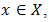
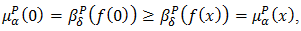 and
and 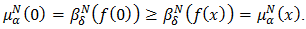 Now, let
Now, let 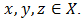 Then
Then 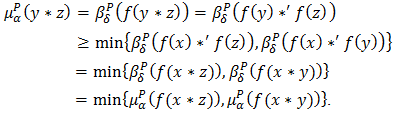 And,
And,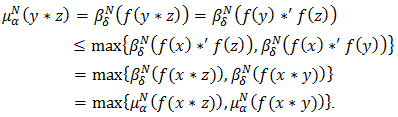 Hence the inverse image of a bipolar fuzzy
Hence the inverse image of a bipolar fuzzy 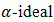 of BP-algebra is also bipolar fuzzy
of BP-algebra is also bipolar fuzzy 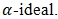 Definition 4.14. A bipolar fuzzy subset
Definition 4.14. A bipolar fuzzy subset 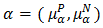 has
has 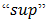 and
and 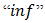 properties if for any subset
properties if for any subset 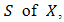 there exist
there exist 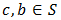 such that
such that 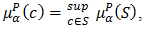 and
and 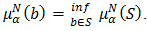 Theorem 4.15. An onto homomorphic image of a bipolar fuzzy
Theorem 4.15. An onto homomorphic image of a bipolar fuzzy 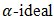 of BP-algebra with
of BP-algebra with 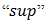 and
and 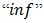 properties is a bipolar fuzzy
properties is a bipolar fuzzy 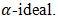 Proof. Let
Proof. Let 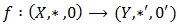 be an onto homomorphism of BP-algebras and
be an onto homomorphism of BP-algebras and 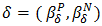 is a bipolar fuzzy
is a bipolar fuzzy 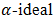 in
in 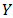 . Let
. Let 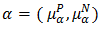 is a bipolar fuzzy
is a bipolar fuzzy 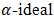 in
in 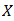 with
with 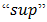 and
and 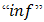 properties. Then for all
properties. Then for all 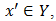 we get
we get 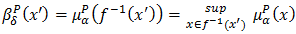 and
and 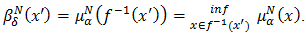 Since
Since 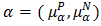 is a bipolar fuzzy
is a bipolar fuzzy 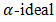 in
in 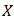 . We have
. We have 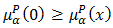 and
and 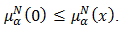 Note that
Note that 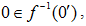 such that and are the zero elements of
such that and are the zero elements of 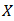 and
and 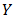 respectively. Thus
respectively. Thus 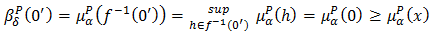 and
and 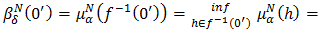
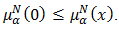 This implies that
This implies that 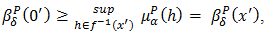 and
and 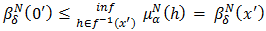 for all
for all 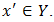 For any
For any 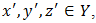 let
let 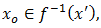
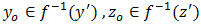 be such that
be such that 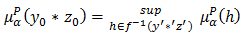 and
and 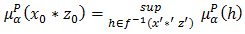 and
and 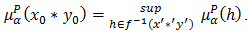 Then
Then 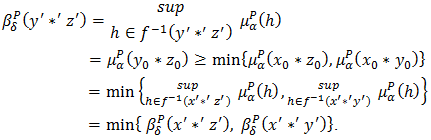 Similarly, we have
Similarly, we have 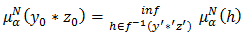 and
and 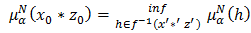 and
and 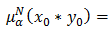
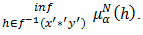 Then
Then  Hence the onto homomorphic image of a bipolar fuzzy
Hence the onto homomorphic image of a bipolar fuzzy  of BP-algebra is also bipolar fuzzy
of BP-algebra is also bipolar fuzzy 
5. Conclusions and Future Research
- To investigate the structure of an algebraic system, it is clear that
 with special properties plays an important role. In the present paper, we have applied the notion of the bipolar fuzzy set theory to
with special properties plays an important role. In the present paper, we have applied the notion of the bipolar fuzzy set theory to 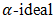 of BP-algebra and investigated some of their useful properties. In the future, these definitions and fundamental results can be applied to some different algebraic structures. There are more topics that could take advantage of
of BP-algebra and investigated some of their useful properties. In the future, these definitions and fundamental results can be applied to some different algebraic structures. There are more topics that could take advantage of 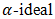 . Like for example cubic intuitionistic
. Like for example cubic intuitionistic 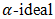 of BP-algebra, cubic fuzzy
of BP-algebra, cubic fuzzy 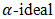 of BP-algebra, and fuzzy soft
of BP-algebra, and fuzzy soft 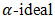 in BP-algebra. There are many other aspects which should be explored and studied in the area of BP-algebra such as anti-fuzzy
in BP-algebra. There are many other aspects which should be explored and studied in the area of BP-algebra such as anti-fuzzy 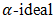 of BP-algebra, interval-valued fuzzy
of BP-algebra, interval-valued fuzzy 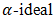 of BP-algebra, intuitionistic fuzzy
of BP-algebra, intuitionistic fuzzy 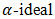 of BP-algebra, doubt intuitionistic fuzzy
of BP-algebra, doubt intuitionistic fuzzy 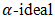 of BP-algebra, fuzzy derivations
of BP-algebra, fuzzy derivations 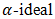 of BP-algebra, and interval-valued intuitionistic fuzzy
of BP-algebra, and interval-valued intuitionistic fuzzy 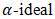 of BP-algebra. It is our hope that this work would other foundations for further study of the theory of BP-algebra.
of BP-algebra. It is our hope that this work would other foundations for further study of the theory of BP-algebra. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML