-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2019; 9(5): 199-202
doi:10.5923/j.ajms.20190905.03

Contraction Conditions in Probabilistic Metric Space
Ajay Kumar Chaudhary1, 2, Kanhaiya Jha1
1Deparmentof Mathematics, School of Science, Kathmandu University, Dhulikhel, Kavre, Nepal
2Department of Mathematics, Tri-Chandra Multiple Campus, Tribhuvan University, Kathmandu, Nepal
Correspondence to: Ajay Kumar Chaudhary, Deparmentof Mathematics, School of Science, Kathmandu University, Dhulikhel, Kavre, Nepal.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The classical Banach contraction principle in metric space is one of the fundamental results in metric space with wide applications. And the probabilistic metric space is one of the important generalizations of metric space introduced by Austrian mathematician Karl Menger in 1942. The purpose of this article is to describe different contraction conditions in Probabilistic Metric Space. Also, mention the generalized contraction conditions and interrelationships between contraction conditions.
Keywords: Fixed Point, t-norm, Probabilistic metric space, Contraction condition
Cite this paper: Ajay Kumar Chaudhary, Kanhaiya Jha, Contraction Conditions in Probabilistic Metric Space, American Journal of Mathematics and Statistics, Vol. 9 No. 5, 2019, pp. 199-202. doi: 10.5923/j.ajms.20190905.03.
Article Outline
1. Introduction and Preliminaries
- In mathematics, analysis plays an important role in the development of mathematics. Among several branches of analysis, functional analysis which deals with the study of several functions, come under Functional Analysis. It describes two types of functional analysis one is linear and another is non-linear functional analysis. Fixed point theory is one of the most important topics of non-linear functional analysis since 1960. It has wide applications to the numerous fields of mathematics as well as outside mathematics such as differential equations, integral equations, variational problems, optimization problems, game theory, graph theory, image and signal processing, economics, and many more.The notion of distance later known as metric space, introduced by M. Frechet in 1906, furnishes the common idealization of a large number of mathematical, physical and other scientific constructs in which the distance of a 'distance' appears. The objects under consideration may be most varied. They may be points, functions, sets, and even the subjective experiences of sensation. What matters is the possibility of associating a non-negative real number with each ordered pair of elements of a certain set, and that the number associated with pairs and triples of such elements satisfy certain conditions. However, in numerous instances in which the theory of metric spaces is applied, this very association of a single number with a pair of elements is, realistically speaking, an over idealization. This is so even in the measurement of an ordinary length, where the number given as the distance between two points is often not the result of a single measurement, but the average of a series of measurements. Indeed, in this and many similar situations, it is appropriate to look upon the distance concept as a statistical rather a determinate one. More precisely, instead of associating a number - the distance
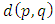 - with every pair of elements
- with every pair of elements 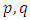 , one should associate a distribution function
, one should associate a distribution function  any for any positive number
any for any positive number 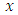 , interpret
, interpret 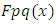 as the probability that the distance from
as the probability that the distance from 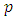 to
to 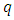 less than
less than 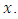 When this is done one obtains a generalization of the concept of metric space - a generalization which was first introduced by Austrian Mathematicians Karl Menger in 1942 and following him, is called a statistical metric space [8]. In this paper, we analyze the different contraction conditions in probabilistic metric space and their inter-relationships. Definition 1.1: Metric space is a pair
When this is done one obtains a generalization of the concept of metric space - a generalization which was first introduced by Austrian Mathematicians Karl Menger in 1942 and following him, is called a statistical metric space [8]. In this paper, we analyze the different contraction conditions in probabilistic metric space and their inter-relationships. Definition 1.1: Metric space is a pair 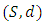 , where
, where 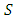 is a non-empty set and
is a non-empty set and 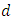 is a distance function or metric of the space defined by
is a distance function or metric of the space defined by 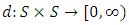 , satisfies the following conditions:
, satisfies the following conditions: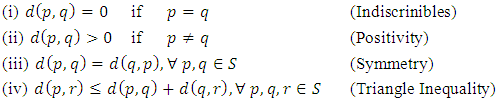 Example 1.1: Let
Example 1.1: Let 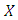 be a non-empty set. For
be a non-empty set. For 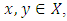 we define
we define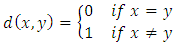 Then,
Then, 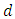 is discrete metric and the space
is discrete metric and the space 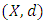 is discrete metric space.Definition 1.2: Let
is discrete metric space.Definition 1.2: Let 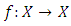 be a map. Then, an element
be a map. Then, an element 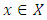 is said to be fixed point of
is said to be fixed point of 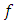 if
if 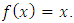 Example 1.2: Let
Example 1.2: Let 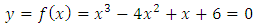 , cubic equation.Then, it can be transferred to as
, cubic equation.Then, it can be transferred to as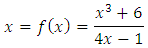 Here,
Here, 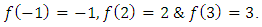 So, by definition
So, by definition 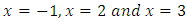 are fixed points of
are fixed points of 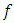 .Definition 1.3: Let
.Definition 1.3: Let 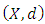 be a metric space and let
be a metric space and let 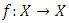 be a mapping. Then,
be a mapping. Then, 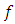 is called contraction if there exists a fixed constant
is called contraction if there exists a fixed constant 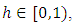 such that
such that 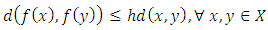 Example 1.3: Let
Example 1.3: Let 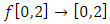 be defined by,
be defined by,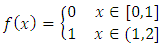 Then,
Then, 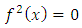 for all
for all 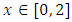 . So,
. So, 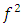 is a contraction on
is a contraction on 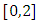 . But
. But 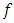 is not continuous and thus not a contraction map.Definition 1.4: For the set
is not continuous and thus not a contraction map.Definition 1.4: For the set 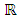 of real numbers, a function
of real numbers, a function 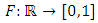 is called a distribution function if(i)
is called a distribution function if(i) 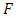 is non-decreasing,(ii)
is non-decreasing,(ii) 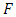 is left continuous, and(iii)
is left continuous, and(iii) 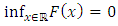 and
and 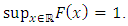 If
If 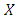 is a non-empty set,
is a non-empty set, 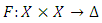 is called probabilistic distance on
is called probabilistic distance on 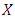 and
and 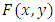 is usually denoted by
is usually denoted by 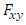 . We will denote by
. We will denote by  the family of all distribution function on
the family of all distribution function on  and
and 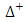 on
on 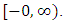 Example 1.4: Let
Example 1.4: Let 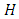 is a maximal element for
is a maximal element for  then, distribution function
then, distribution function 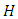 is defined by
is defined by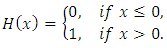
 | Figure 1. Distribution Function |
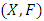 where
where 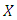 is a non-empty set and
is a non-empty set and 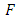 is a function defined by
is a function defined by 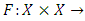
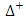 (the set of all distribution functions) that is
(the set of all distribution functions) that is 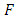 associates a distribution function
associates a distribution function 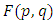 with every pair
with every pair 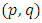 of points in
of points in 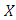 . The distribution function
. The distribution function 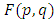 is denoted by
is denoted by 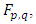 whence the symbol
whence the symbol 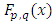 will represent the value of
will represent the value of 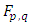 at
at 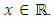 And the function
And the function 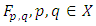 are assumed to satisfy following conditions:(i)
are assumed to satisfy following conditions:(i) 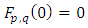 ; (ii)
; (ii) 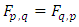 , (iii)
, (iii) 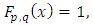 for every
for every 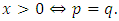 (iv) For every
(iv) For every 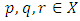 and for every
and for every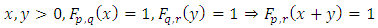 The interpretation of
The interpretation of 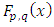 as the probability that the distance from
as the probability that the distance from 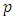 to
to 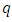 is less than
is less than 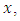 it is clear that PM condition (iii), (i) and (ii) are straight forward generalizations of the corresponding metric space conditions (i), (ii) and (iii). The PM condition (iv) is a 'minimal' generalization of the triangle inequality of metric space condition (iv). If it is certain that the distance of
it is clear that PM condition (iii), (i) and (ii) are straight forward generalizations of the corresponding metric space conditions (i), (ii) and (iii). The PM condition (iv) is a 'minimal' generalization of the triangle inequality of metric space condition (iv). If it is certain that the distance of 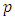 and
and 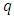 is less than
is less than 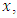 and like wise certain that the distance of
and like wise certain that the distance of 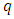 and
and 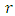 is less than
is less than 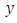 , then it is certain that the distance of
, then it is certain that the distance of 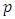 and
and 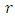 is less than
is less than 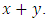 The PM condition (iv) is always satisfied in metric spaces, where it reduces to the ordinary triangle inequality.Definition 1.6: [6] A mapping
The PM condition (iv) is always satisfied in metric spaces, where it reduces to the ordinary triangle inequality.Definition 1.6: [6] A mapping 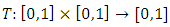 is called a triangular norm (shortly t-norm) if for all
is called a triangular norm (shortly t-norm) if for all 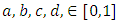 the following conditions are satisfied:
the following conditions are satisfied: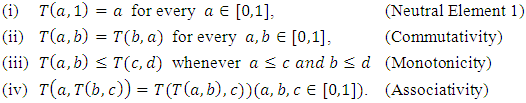 Example 1.5 of t-norms
Example 1.5 of t-norms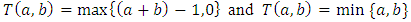 The four basic standard t-norms are:(i) The minimum t-norm,
The four basic standard t-norms are:(i) The minimum t-norm, 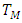 , is defined by
, is defined by 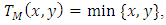 (ii) The product t-norm,
(ii) The product t-norm, 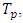 is defined by
is defined by 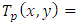
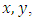 (iii) The Lukasiewicz t-norm,
(iii) The Lukasiewicz t-norm, 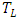 , is defined by
, is defined by 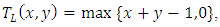 (iv) The weakest t-norm, the drastic product,
(iv) The weakest t-norm, the drastic product, 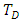 , is defined by
, is defined by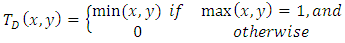 With references to the point wise ordering, we have the following inequalities
With references to the point wise ordering, we have the following inequalities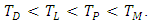 Definition 1.7: [8] A Menger probabilistic metric space (briefly, Menger PM-space) is a triple
Definition 1.7: [8] A Menger probabilistic metric space (briefly, Menger PM-space) is a triple 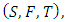 where
where 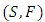 is a probabilistic metric space,
is a probabilistic metric space, 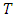 is a triangular norm and also satisfies the following conditions, for all
is a triangular norm and also satisfies the following conditions, for all 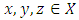 and
and 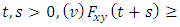
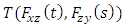 . This is the extension of triangle inequality. This inequality is called Menger's triangle inequality.Example 1.6: Let
. This is the extension of triangle inequality. This inequality is called Menger's triangle inequality.Example 1.6: Let 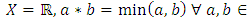
 and
and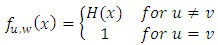 where
where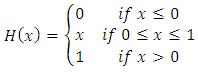 then
then 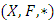 is Menger Space.Definition 1.8: [4] Let
is Menger Space.Definition 1.8: [4] Let 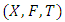 be a Menger Space and
be a Menger Space and 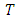 be a continuous t-norm (1) A sequence
be a continuous t-norm (1) A sequence 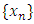 in
in 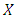 is said to be converge to a point
is said to be converge to a point 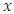 in
in 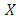 (written
(written 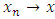 ) iff for every
) iff for every 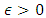 and
and 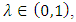 there exists an integer
there exists an integer 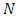 such that
such that 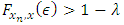 for all
for all 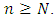 (2) A sequence
(2) A sequence 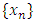 in
in 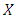 is called a Cauchy if for every
is called a Cauchy if for every 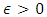 and
and 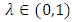 , there exists an integer
, there exists an integer 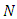 such that
such that 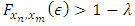 for all
for all 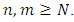 (3) A Menger space in which every Cauchy sequence is convergent is said to be Complete Menger Space.Banach Contraction Condition in Metric Space: The most basic fixed-point theorem is analysis known as the Banach Contraction Principle (BCP). It is due to S. Banach [1] and appeared in his Ph.D. thesis (1920, published in 1922). The BCP was first stated and proved by Banach for the Contraction maps in setting of complete normed linear spaces. At about the same time the concept of an abstract metric space was introduced by Hausdorff for the set valued mappings, which then provided the general framework for the principle for contraction mappings in a complete metric space. The BCP can be applied to mappings which are differentiable, or more generally, Lipschitz continuous.Theorem 1.1: Let
(3) A Menger space in which every Cauchy sequence is convergent is said to be Complete Menger Space.Banach Contraction Condition in Metric Space: The most basic fixed-point theorem is analysis known as the Banach Contraction Principle (BCP). It is due to S. Banach [1] and appeared in his Ph.D. thesis (1920, published in 1922). The BCP was first stated and proved by Banach for the Contraction maps in setting of complete normed linear spaces. At about the same time the concept of an abstract metric space was introduced by Hausdorff for the set valued mappings, which then provided the general framework for the principle for contraction mappings in a complete metric space. The BCP can be applied to mappings which are differentiable, or more generally, Lipschitz continuous.Theorem 1.1: Let 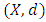 be a complete metric space, then each contraction map
be a complete metric space, then each contraction map 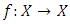 has a unique fixed point.Example 1.7:
has a unique fixed point.Example 1.7: 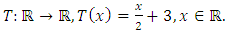 Obviously
Obviously 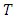 is a Banach contraction and
is a Banach contraction and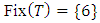 where
where 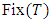 denotes the fixed point of the mapping
denotes the fixed point of the mapping 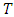 .
.2. Contraction Conditions in Probabilistic Metric Space
2.1. V.M. Seghal and A.T. Bharucha-Reid (B) Contraction Conditions in PM Space
- The following definition of a contraction mapping was suggested and studied by V.M. Seghal and A.T. Bharucha-Reid in 1972, which is very natural probabilistic version of the notion of Banach contraction in metric space. Definition 2.1.1: [12] The following definition of a contraction mapping was suggested and studied by V.M. Seghal and A.T. Bharucha-Reid in 1972, which is very natural probabilistic version of the notion of Banach contraction in metric space.Let
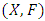 be a probabilistic metric space. A mapping
be a probabilistic metric space. A mapping 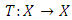 is a contraction mapping (or a SB - Contraction mapping or B-contraction) on
is a contraction mapping (or a SB - Contraction mapping or B-contraction) on 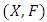 if and only if there is a
if and only if there is a 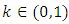 such that
such that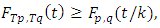 | (2.1) |
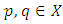 and
and 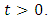 It is also known as probabilistic k-contraction.The geometrical interpretation expression (2.1) is that the probability that the distance between the image points
It is also known as probabilistic k-contraction.The geometrical interpretation expression (2.1) is that the probability that the distance between the image points 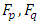 being less than
being less than 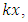 is at least equal to the probability that the distance between
is at least equal to the probability that the distance between 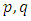 that is less than
that is less than 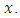 Dentition 2.1.2: [2] Let
Dentition 2.1.2: [2] Let 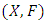 be a probabilistic metric space. A mapping
be a probabilistic metric space. A mapping 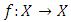 is a probabilistic q-contraction
is a probabilistic q-contraction 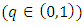 if
if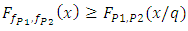 | (2.2) |
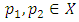 and every
and every 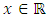 It is obvious that
It is obvious that 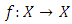 is a probabilistic q-contraction if and only if for every
is a probabilistic q-contraction if and only if for every 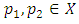 and every
and every 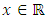 the following implication holds
the following implication holds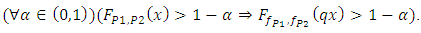 | (2.3) |
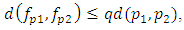 where
where 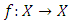 and
and 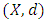 is a metric space. In order to prove that (2.3) implies (2.2) recall that every metric space
is a metric space. In order to prove that (2.3) implies (2.2) recall that every metric space 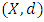 is also a Menger space
is also a Menger space 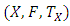 , if
, if 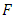 is defined in the following way:
is defined in the following way: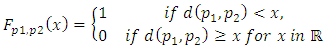 | (2.4) |
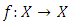 is such that (2.3) holds and prove that (2.2) is satisfied i.e.,that for every
is such that (2.3) holds and prove that (2.2) is satisfied i.e.,that for every 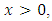 we have
we have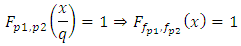 If
If 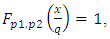 then
then 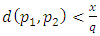 and (2.3) implies
and (2.3) implies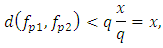 which means that
which means that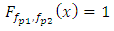
2.2. Hick’s Contraction (C) in PM Space
- Definition 2.2.1: [7] T.L. Hicks in 1996, defined the following C-contraction mapping in PM space.Let
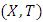 be a probabilistic metric space and
be a probabilistic metric space and 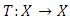 . The mapping
. The mapping 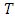 is called Hicks C-contraction (or, C-contraction) if there exists
is called Hicks C-contraction (or, C-contraction) if there exists 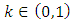 such that the following implication holds for every
such that the following implication holds for every 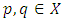 : and for every
: and for every 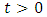
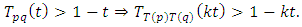 Definition 2.2.2: [9] D.Mihet in 2005, introduced the weak- hicks contraction in PM Space as follows:Let
Definition 2.2.2: [9] D.Mihet in 2005, introduced the weak- hicks contraction in PM Space as follows:Let 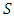 be a nonempty set and
be a nonempty set and  be a probabilistic distance on
be a probabilistic distance on 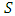 . A mapping
. A mapping 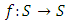 is said to be weak - Hicks contraction (w-H contraction) if there exists
is said to be weak - Hicks contraction (w-H contraction) if there exists 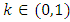 such that, for all
such that, for all 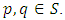
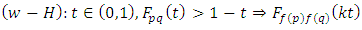
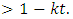 Example 2.2.1: Let
Example 2.2.1: Let 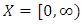 and
and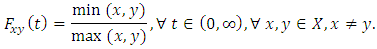 It is known ([10], [11]) that
It is known ([10], [11]) that 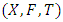 is a complete Menger space under the triangular norm
is a complete Menger space under the triangular norm 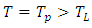 . Also, it can easily be seen that the mapping
. Also, it can easily be seen that the mapping 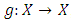 ,
,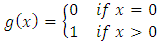 is a w-H contraction for every
is a w-H contraction for every 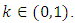
2.3. Generalization of Bharucha (B)-Contraction
- As a generalization of the notion of a probabilistic B-contraction, we shall introduce the notion of a probabilistic (m,k) - B-contraction where
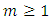 and
and 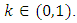 Definition 2.3.1: [6] If
Definition 2.3.1: [6] If 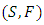 is a PM - space,
is a PM - space, 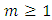 and
and 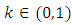 , a function
, a function 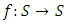 is called probabilistic (m,k)-B-contraction if for any
is called probabilistic (m,k)-B-contraction if for any 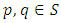 there is an
there is an 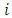 with
with 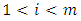 such that for every
such that for every 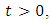
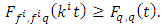 If
If 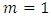 and
and 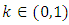 then a probabilistic
then a probabilistic 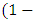
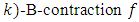 is a probabilistic B-contraction.As a generalization of C-contraction, we haveDefinition 2.3.2: [6] If
is a probabilistic B-contraction.As a generalization of C-contraction, we haveDefinition 2.3.2: [6] If 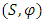 is a PM - space,
is a PM - space, 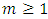 and
and 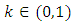 , a function
, a function 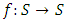 is called a (m,k)-C-contraction if for any
is called a (m,k)-C-contraction if for any 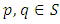 there is an
there is an 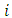 with
with 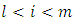 such that for every
such that for every 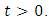
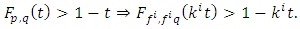 If
If 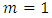 and
and 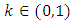 then a probabilistic
then a probabilistic 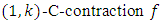 is a probabilistic C-contraction.
is a probabilistic C-contraction.2.4. Probabilistic G-contraction Mapping
- Definition 2.5.1: [5] g-contraction mapping is the generalization of Hick’s C-contraction in Probabilistic Metric Space. Let
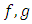 be two mappings defined on a Menger space
be two mappings defined on a Menger space 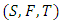 with values into itself and let us suppose that
with values into itself and let us suppose that 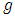 is bijective. The mapping
is bijective. The mapping 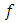 is called a probabilistic g-contraction with a constant
is called a probabilistic g-contraction with a constant 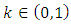 if
if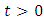 and
and 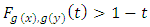 impies
impies 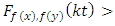
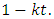 The notion of g-contraction is justified because the images of two points
The notion of g-contraction is justified because the images of two points 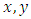 under the function
under the function 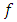 are nearer than images of the same points under the function
are nearer than images of the same points under the function 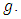
3. Conclusions [3]
- The Probabilistic g-contraction is Hicks C-contraction when g = I, an identity mapping. Since H-contraction need not be B-contraction. So, Probabilistic g-contraction need not be B-contraction. Moreover, C-contraction is an extension of Banach contraction in Probabilistic Metric Space.It is clear that(i) (m-k) contraction
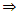 C-contraction
C-contraction 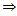 B-contraction
B-contraction 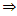 Banach contraction(ii) g-contraction
Banach contraction(ii) g-contraction 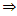 C-contraction
C-contraction 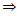 B-contraction(iii) C-contraction
B-contraction(iii) C-contraction 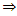 (w-H) contraction
(w-H) contraction Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML