-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2019; 9(4): 151-159
doi:10.5923/j.ajms.20190904.01

Modelling the Volatility of the Price of Bitcoin
Kofi Agyarko, Albert Buabeng, Joseph Acquah
University of Mines and Technology, Department of Mathematical Sciences, Tarkwa, Ghana
Correspondence to: Kofi Agyarko, University of Mines and Technology, Department of Mathematical Sciences, Tarkwa, Ghana.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This study assessed the volatility and the Value at Risk (VaR) of daily returns of Bitcoins by conducting a comparative study in the forecast performance of symmetric and asymmetric GARCH models based on three different error distributions. The models employed are the SGARCH and TGARCH which were validated based on AIC, MAE and MSE measures. The results indicated that the SGARCHGED (1,1) with generalised error distribution term was identified as the best fitted GARCH model. Though, this best fitted model based on information loss (AIC) did not provide the best out-of-sample forecast, the differences was insignificant. Thus, the study clearly demonstrates that it is reliable to use the best fitted model for volatility forecasting. Also, to further validate the performance of the best fitted model, it was subjected to a historical back-test using Value at Risk (VaR). Though, it was evident from the study that no model was superior, it was indicated that an average loss of 1.2% is expected to be exceeded only 1% of the time. Moreover, volatility forecast from the back testing was relatively high during the first quarter of 2018 but begun decreasing steadily with time.
Keywords: Volatility, Bitcoin, GARCH models, Value at Risk
Cite this paper: Kofi Agyarko, Albert Buabeng, Joseph Acquah, Modelling the Volatility of the Price of Bitcoin, American Journal of Mathematics and Statistics, Vol. 9 No. 4, 2019, pp. 151-159. doi: 10.5923/j.ajms.20190904.01.
Article Outline
1. Introduction
- The recent development in the field of cryptocurrency is receiving significant attention as it has become a significant means of making day to day business transactions. It is based on a fundamentally new technology, designed to work as a medium of exchange that uses cryptography to control its creation and management, rather than relying on central authorities [1]. Hence, its potential of which is not fully understood [2].The most traded currency of the cryptocurrencies, Bitcoin, over the years has undergone rapid growth to become a significant currency both on and offline to the extent that some businesses has begun accepting Bitcoin in addition to traditional currencies. In the field of investment, the recent rise in the value of Bitcoin has led most investors to consider it as an investment opportunity, although several regulatory agencies have issued investor alerts about it.Although, Bitcoin has been criticized for its use in illegal transactions, its high electricity consumption, price volatility, thefts from exchanges and the possibility that it is an economic bubble [3], its legal status varies substantially from country to country. Whereas many countries do not make the usage of bitcoin itself illegal, its status as money (or a commodity) varies with differing regulatory implications, thus, becoming a source of worry for investors and therefore needs due attention.In the field of finance, one way to understand the dynamics of such volatile phenomenon is to investigate its returns and assess how investors and the markets value its prospects. In modelling such volatilities, a fundamental methodology is to measure potential losses of investment. Thus, the concept of Value at Risk (VaR), has become a widespread measure of market risk. However, the estimation of VaR requires the use of the Auto Regressive Conditional Heteroscedasticity (ARCH) model by [4], later generalized independently by [5] and [6] into the symmetric Generalized ARCH (GARCH). A thorough survey by [7] finds that GARCH generally dominates ARCH. Today, several extensions of the traditional symmetric GARCH (p,q) model have been introduced to increase the flexibility of the original GARCH model such as asymmetric GARCH model which consist of the exponential GARCH (EGARCH), GJR-GARCH of [8], and the threshold GARCH (TGARCH) of [9]. These asymmetric GARCH models capture the characteristic of volatility and are today the most popular way of parameterizing this dependence as they tend to outperform the original GARCH by incorporating leverage effects [10].In literature, various studies in attempt to improve volatility forecasting using GARCH introduces various error distribution ([11]; [12]; [13]). Though, several arguments have been made regarding the superiority among the error distributions, this study employs the three of the frequently used, namely: the Normal distribution (NORM), Student-t (STD), Generalized Error Distribution (GED). The main reason for choosing these types of error distributions is to consider the skewness, excess kurtosis and heavy-tails of return distributions. Hence, this study seeks to model the volatility and Value at Risk of the daily returns of Bitcoins using symmetric and asymmetric GARCH models, given three different assumptions of the error distribution.
2. Material and Methods Used
2.1. Scope
- Historical data on the daily prices of bitcoin online was taken from CoinMarketCap website (www.coinmarketcap.com/currencies/bitcoin/historical-data). The data spans from January 1, 2017 to September 12, 2018 totaling 620 observations. The daily closing prices was used in this paper.
2.2. Methods
- The daily closing prices were changed to log returns given by Equation (1);
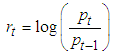 | (1) |
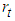 is the logarithmic return at time
is the logarithmic return at time 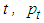 is the current closing price at time t and
is the current closing price at time t and 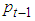 is the previous closing price.
is the previous closing price.2.2.1. Jarque-Bera Test
- Jarque-Bera test is a goodness-of-fit test which examines if the sample data have kurtosis and skewness similar to a normal distribution. The test is given by Equation (2);
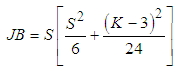 | (2) |
2.2.2. Unit Root Test: ADF Test
- The Augmented Dickey-Fuller (ADF) test was used to determine whether the individual series studied have unit root or were covariance stationary. This method was proposed by [14] as an upgraded form of Dickey-Fuller Test. The unit root test is done under the null hypothesis
 (non-stationary) against the alternate
(non-stationary) against the alternate 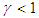 (covariance stationary). Where
(covariance stationary). Where 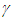 is the characteristic root of an AR polynomial. The ADF test statistic is given by Equation (3);
is the characteristic root of an AR polynomial. The ADF test statistic is given by Equation (3);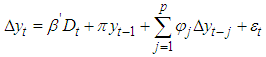 | (3) |
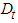 is a vector of deterministic terms (constant, trend etc.). The plagged difference terms,
is a vector of deterministic terms (constant, trend etc.). The plagged difference terms, 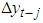 , are used to approximate the mean equation structure of the errors,
, are used to approximate the mean equation structure of the errors, 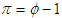 , and the value of p is set so that the error,
, and the value of p is set so that the error, 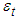 is serially uncorrelated.Contrary to most unit root test, like ADF, the absence of a unit root is not a proof of stationarity, but by design, of trend-stationarity. This is being addressed by the Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test developed by [15]. KPSS is defined by Equation (4)
is serially uncorrelated.Contrary to most unit root test, like ADF, the absence of a unit root is not a proof of stationarity, but by design, of trend-stationarity. This is being addressed by the Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test developed by [15]. KPSS is defined by Equation (4)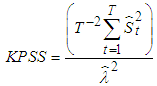 | (4) |
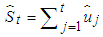 ,
, 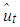 is the residual of a regression of
is the residual of a regression of 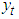 on
on 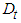 and
and 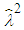 is a consistent estimate of the long-run variance of
is a consistent estimate of the long-run variance of 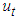 using
using 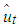 .
.2.2.3. The Mean Equation
- It is imperative to specify an appropriate mean equation in modelling volatility. Following [16], this paper used the mean equation given by Equation (5);
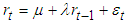 | (5) |
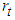 is the returns at time,
is the returns at time, 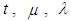 and
and 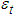 are constants and the innovation respectively.
are constants and the innovation respectively.2.2.4. Univariate GARCH Models
- The returns of a financial asset largely depend on its volatility. In order to model such a phenomenon, the ARCH and then GARCH models by [4] and [5], respectively, needs to be considered. In GARCH models, the density function is usually written in terms of the location and scale parameters, with normalization vector given by Equation (6)
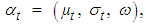 | (6) |
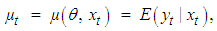 | (7) |
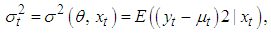 | (8) |
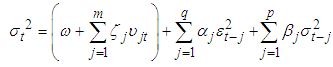 | (9) |
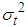 denotes the conditional variance,
denotes the conditional variance, 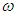 the intercept and
the intercept and 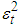 the residuals from the mean filtration process. The GARCH order is defined by (q, p) (ARCH, GARCH). One of the key features of the observed behavior of financial data which GARCH models capture is volatility clustering which may be quantified in the persistence parameter,
the residuals from the mean filtration process. The GARCH order is defined by (q, p) (ARCH, GARCH). One of the key features of the observed behavior of financial data which GARCH models capture is volatility clustering which may be quantified in the persistence parameter, 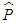 , defined as Equation (10)
, defined as Equation (10)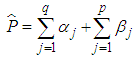 | (10) |
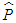 ), is the half-life (H), defined as the number of days it takes for half of the expected reversion back towards
), is the half-life (H), defined as the number of days it takes for half of the expected reversion back towards 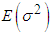 to occur. H is expressed as Equation (11)
to occur. H is expressed as Equation (11)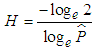 | (11) |
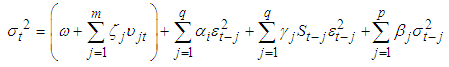 | (12) |
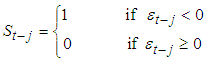 From the model, depending on whether
From the model, depending on whether 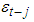 is above or below the threshold value of zero,
is above or below the threshold value of zero, 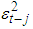 can have different effects on the conditional variance
can have different effects on the conditional variance 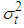 . The persistence of the model
. The persistence of the model 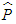 is given by Equation (13)
is given by Equation (13)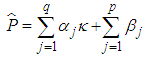 | (13) |
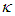 is the expected value of the standardized residuals below zero, and the half-life H is estimated using Equation (11).
is the expected value of the standardized residuals below zero, and the half-life H is estimated using Equation (11).2.2.5. Distributional Assumptions of Error Term
- In GARCH model specification, it is more appropriate to consider the choice on the distributional assumption of the error term. This study assumed three distributional assumptions; Normal distribution (NORM), Student-t distribution (STD) and the Generalized Error Distribution (GED) in order to account for fat tails that are common in most financial data. Normal Distribution (NORM)For the models to fully function, the error term must have zero mean. That is
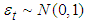 where the error term in this case is normally distributed with zero mean and variance one. The density function for the Normal distribution is given by Equation (14)
where the error term in this case is normally distributed with zero mean and variance one. The density function for the Normal distribution is given by Equation (14)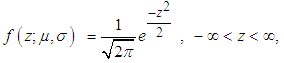 | (14) |
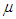 constitute the mean and
constitute the mean and 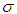 is the standard deviation.Student-t Distribution (STD)The fatter tails, frequently observed in financial time series, are allowed for in the Student’s t distribution assumed by [17] which is given by the density function shown as Equation (15)
is the standard deviation.Student-t Distribution (STD)The fatter tails, frequently observed in financial time series, are allowed for in the Student’s t distribution assumed by [17] which is given by the density function shown as Equation (15)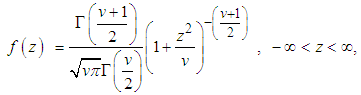 | (15) |
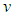 denotes the number of degrees of freedom and
denotes the number of degrees of freedom and 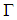 denotes the Gamma function.Generalized Error Distribution (GED)[11] proposed the use of the GED in order to account for fat-tails observed commonly in financial time series. It is given by Equation (16);
denotes the Gamma function.Generalized Error Distribution (GED)[11] proposed the use of the GED in order to account for fat-tails observed commonly in financial time series. It is given by Equation (16);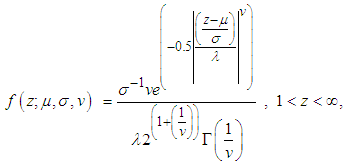 | (16) |
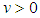 is the degrees of freedom or tail-thickness parameter. If
is the degrees of freedom or tail-thickness parameter. If 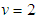 , the GED yields the normal distribution. If
, the GED yields the normal distribution. If 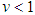 , the density function has thicker tails than the normal density function, whereas for
, the density function has thicker tails than the normal density function, whereas for 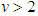 it has thinner tails.
it has thinner tails.2.2.6. Model Selection Criterion
- Two information criteria were used for model selection in this study. They are Akaike Information Criteria (AIC) and the Bayesian Information Criterion (BIC). AIC and BIC are defined as Equations (17) and (18) respectively:
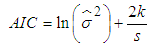 | (17) |
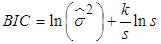 | (18) |
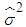 is the variance of the residuals, s is the sample size, k is the total number of parameters. For a GARCH (p,q) model,
is the variance of the residuals, s is the sample size, k is the total number of parameters. For a GARCH (p,q) model, 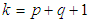 . The best model is the model that has least AIC and BIC values.
. The best model is the model that has least AIC and BIC values.2.2.7. Model Diagnostics
- It is very essential to perform a diagnostic check on the model after determining the best model and its corresponding distribution for the error term to establish whether the model and distribution are correctly specified. This study employs the Ljung-Box and Lagrange Multiplier (LM) tests to test for the presence of autocorrelation and ARCH effects respectively. The presence of autocorrelation and ARCH effects for the residuals of both the mean model and the volatility models will be tested using these two diagnostics.Univariate Ljung-Box TestThe Ljung-Box Test is used to test whether there exist autocorrelations in the residuals of a model. The statistic is given by Equation (19);
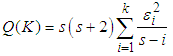 | (19) |
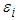 is the residual sample autocorrelation at lag i, s is the size of the series, k is the number of time lags included in the test.
is the residual sample autocorrelation at lag i, s is the size of the series, k is the number of time lags included in the test. 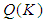 has an approximately chi-square distribution with k degree of freedom.Testing for ARCH EffectsIn applying GARCH methodology it is imperative to examine the residuals for any evidence of ARCH effects. The Lagrange Multiplier (LM) and the Ljung-Box statistic tests are used to test the ARCH effect in the residuals of a model by letting the
has an approximately chi-square distribution with k degree of freedom.Testing for ARCH EffectsIn applying GARCH methodology it is imperative to examine the residuals for any evidence of ARCH effects. The Lagrange Multiplier (LM) and the Ljung-Box statistic tests are used to test the ARCH effect in the residuals of a model by letting the 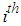 lag autocorrelation of the squared residuals to be
lag autocorrelation of the squared residuals to be 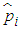 , the Ljung-Box statistic is given by Equation (20);
, the Ljung-Box statistic is given by Equation (20);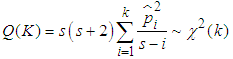 | (20) |
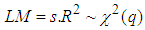 | (21) |
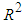 forms the regression.
forms the regression.2.2.8. Evaluation of Volatility Forecast
- To evaluate the forecasting performance of the GARCH models, this study made use of two error measures; Mean Absolute Error (MAE) and the Mean Square Error (MSE). The MAE and MSE are defined as Equations (22) and (23) respectively
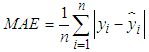 | (22) |
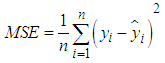 | (23) |
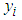 is the
is the 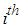 observed value;
observed value; 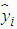 is the
is the 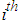 fitted value; n is the sample size.In situations where the best fitted models do not provide the best volatility forecasts in terms of the values of MSE and MAE, the Percent Error (PE) of MSE/MAE for each underlying case is evaluated. This will help investigate the difference of the values of MSE/MAE given by the best fitted model and the best performance model. PE is defined as Equation (24)
fitted value; n is the sample size.In situations where the best fitted models do not provide the best volatility forecasts in terms of the values of MSE and MAE, the Percent Error (PE) of MSE/MAE for each underlying case is evaluated. This will help investigate the difference of the values of MSE/MAE given by the best fitted model and the best performance model. PE is defined as Equation (24)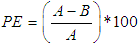 | (24) |
2.2.9. Value-at-Risk
- VaR can be viewed as a gauge that summarizes the worst loss over a target horizon that will not be exceeded with a given level of confidence [18]. More formally,
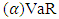 is expressed as Equation (25)
is expressed as Equation (25)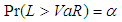 | (25) |
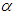 is the significance level. VaR is therefore a quantile in the distribution of profit and loss that is expected to be exceeded only with a certain probability, which is given Equation (26)
is the significance level. VaR is therefore a quantile in the distribution of profit and loss that is expected to be exceeded only with a certain probability, which is given Equation (26)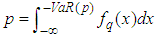 | (26) |
2.2.10. Backtesting VaR
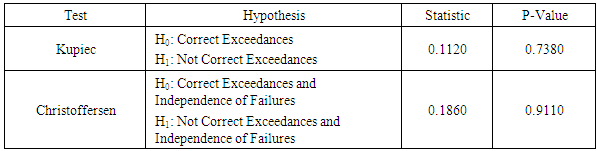
- Finding suitable forecast models for VaR estimates requires a method for evaluating the predictions ex-post. The VaR estimates in this study would be evaluated using two tests: an unconditional and a conditional test of coverage originally developed by [19].Thus, daily returns would be labelled according to Equation (27) in order to define whether the daily return exceeded the VaR estimate or not. The indicator variable is constructed as shown in Equation (27)
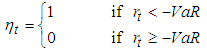 | (27) |
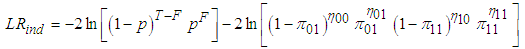 | (28) |
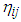 is the number of observations with the value i followed by j for
is the number of observations with the value i followed by j for 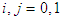 and
and 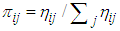 is the corresponding probabilities.
is the corresponding probabilities. 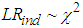 under the null hypothesis which states that the violations are independently distributed. Hence, a rejection of the null hypothesis infers that the violations are clustered and consequently not independent.
under the null hypothesis which states that the violations are independently distributed. Hence, a rejection of the null hypothesis infers that the violations are clustered and consequently not independent.3. Results and Discussions
3.1. Preliminary Analysis of Data
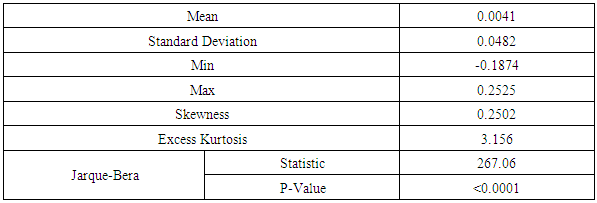
- The descriptive statistics of return of Bitcoins is presented in Table 1. As observed, the average return within the study period was 0.0041. The returns showed a positive skewness with indication of leptokurtic (Excess Kurtosis > 3) depicting increased in probability at the higher quantiles (heavy and longer right tails). Also, the return series does not follow a normal distribution since normality test for it is firmly rejected by the Jarque-Bera statistics (P-Value < 0.05).
|
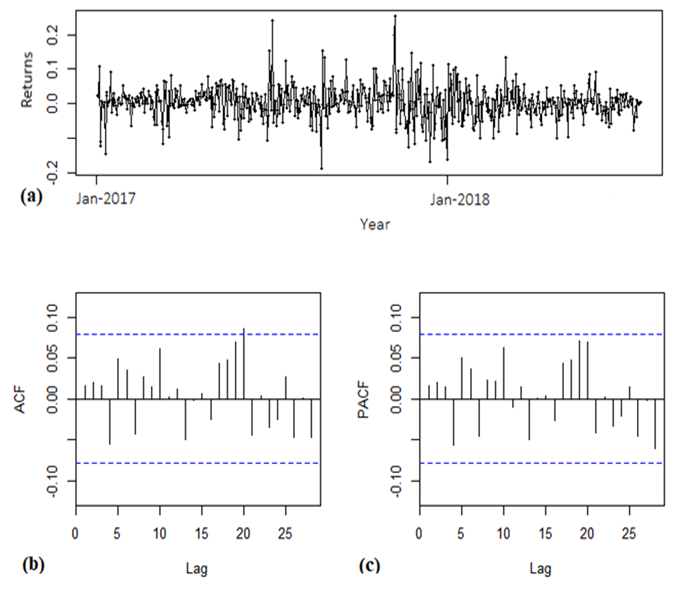 | Figure 1. Time Series Plot of Daily Returns of Bitcoins |
|
|
|
3.2. GARCH Modelling
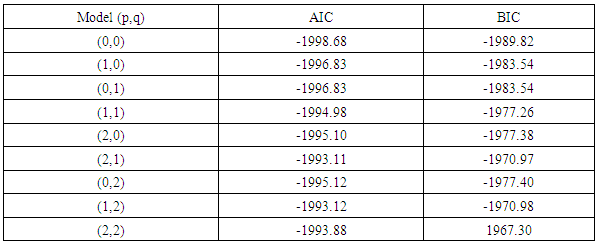
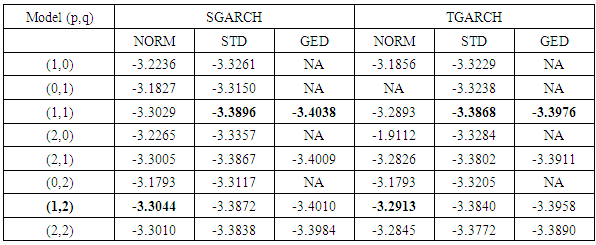
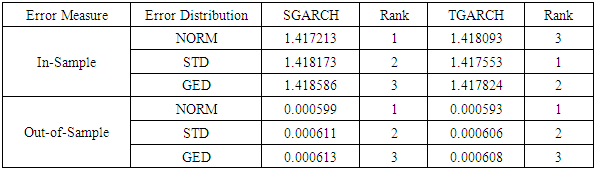
- For the purpose of cross validation, the series is divided into two subsets. The first subset is called in-sample data set (full sample with 31-days/one month shorter, i.e. up to end of 11th August 2018) used to build the GARCH models for underlying return series. The second subset, called out-sample data set (the remaining sample from 11th August, 2018 to the end) is then used to validate the performance of volatility forecasting. Table 5 shows the Akaike Information Criteria (AIC) for the various combinations of the symmetric and asymmetric GARCH models computed under three (3) different error terms distributions.
|
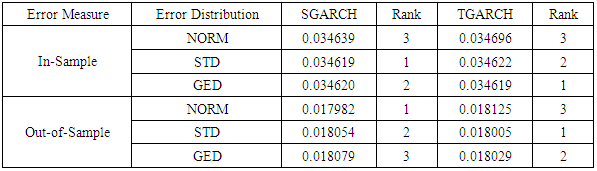
3.2.1. Performance of Volatility Forecasting
- In order to ascertain the validity of [22] findings and determine the appropriate GARCH model, the volatility forecast performance from the in-sample and out-of-sample models were evaluated. Table 6 and 7 shows the evaluation of the best fitted GARCH models under each error distributions using two error measures (MAE and MSE).
|
|
|
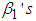 were significant (p-values<0.05) suggesting that volatility is persistent in the sense that the volatility of time
were significant (p-values<0.05) suggesting that volatility is persistent in the sense that the volatility of time 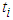 is greatly affected by the volatility at time
is greatly affected by the volatility at time 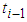 . Also, all the
. Also, all the 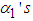 have their p-values less than 0.05 implying that the volatilities are less spiky since a shock at time
have their p-values less than 0.05 implying that the volatilities are less spiky since a shock at time 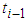 (caused by an unusually high or low return) affects the volatility of time
(caused by an unusually high or low return) affects the volatility of time 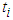 . With regards to the
. With regards to the 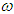 , only SGARCHGED (1,1) has p-values greater than 0.05. The fact that
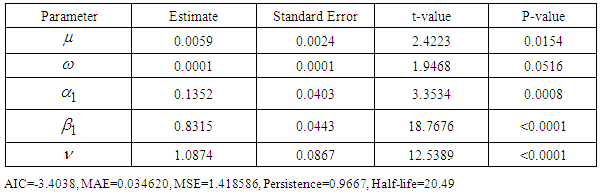
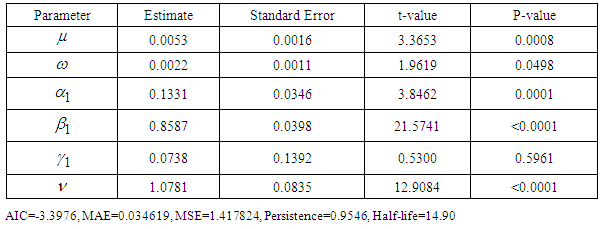
, only SGARCHGED (1,1) has p-values greater than 0.05. The fact that 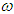 is not different from zero means that the unconditional long run variance is zero. Also, the estimated volatility persistence is very high for all best fitted models and implies half-lives of shocks to volatility to SGARCHGED (1,1) and TGARCHGED (1,1) of 20 and 15 days, respectively. The shape parameter
is not different from zero means that the unconditional long run variance is zero. Also, the estimated volatility persistence is very high for all best fitted models and implies half-lives of shocks to volatility to SGARCHGED (1,1) and TGARCHGED (1,1) of 20 and 15 days, respectively. The shape parameter 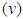 , showing the estimated degrees of freedom are slightly different from each other which implies that the density plot of all the best fitted models would look the same.
, showing the estimated degrees of freedom are slightly different from each other which implies that the density plot of all the best fitted models would look the same.
|
|
3.2.2. Model Diagnostics
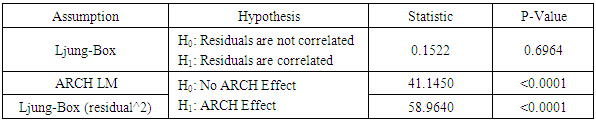
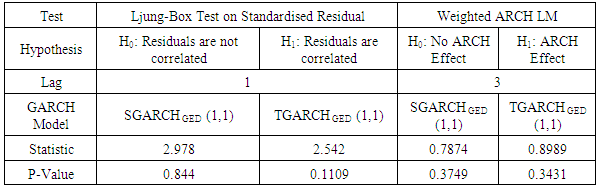
- Table 11 shows the diagnostics on the best fitted GARCH models (SGARCHGED (1,1) and TGARCHGED (1,1)). As observed, the Ljung-Box test null hypothesis is not rejected at 5% significance level. This indicates that the standardized residuals are considered as white noise. Also, the weighted ARCH LM test indicates the presence of no ARCH effects in the models. These tests collectively suggest that the best fitted GARCH models are sufficient to correct the serial correlation of the return’s series in the conditional variance equation.
|
3.3. Returns of Bitcoins with 1% VaR Limits
- To validate the performance of the best fitted GARCH models, it is useful to perform a historical back-test to compare the estimated Value at Risk (VaR) with the actual return over the study period. If the return is less than the VaR in most cases, we have a VaR exceedance. In this study, a VaR exceedance is set to occur only in 1% of the cases, hence, the tests are evaluated on the 1% significance level. The start period of the back-test is set to 347 after the beginning of the series (i.e., January 2018). Also, The GARCH parameters are subsequently updated throughout the data set using rolling window estimation instead of being held constant over time. This is made in order to achieve flexibility in the parameters. The plot of the back-testing performance is shown in Figure 2.
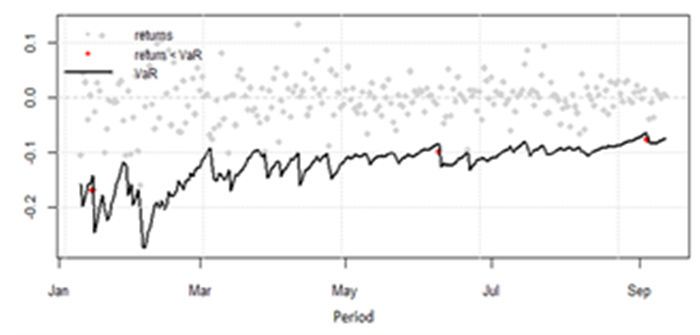 | Figure 2. 1% VaR Forecast at 1% |
|
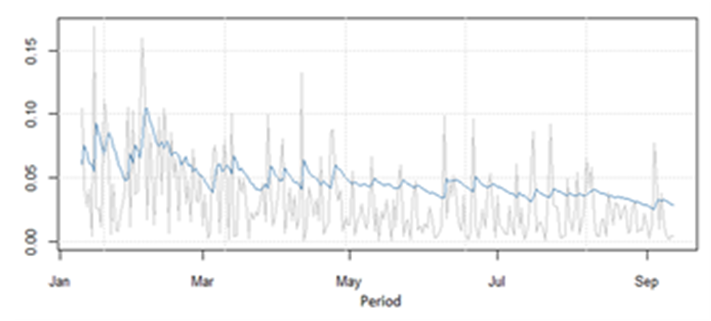 | Figure 3. Forecast of Volatility vs Daily Returns of Bitcoins (Absolute) |
4. Conclusions
- This paper modelled volatility and the Value at Risk (VaR) of daily returns of Bitcoins by conducting a comparative study in the forecast performance of symmetric and asymmetric GARCH models based on three different type of error distributions. The models include SGARCH and TGARCH. The performance of the models was evaluated using AIC, MAE and MSE. The results indicated that the SGARCHGED (1,1) with generalised error distribution term was identified as the best fitted GARCH model computed based on the AIC criterion. This indeed provides a compelling evidence made that it is difficult to find a volatility model that outperforms the simple GARCH (1,1) basically due to its better numerical stability of estimation and parsimony. Though, these bests fitted model based on information loss (AIC) did not provide the best out-of-sample forecast, the error measures (MAE/MSE values) given by the best fitted models were insignificantly different from that given by the best forecast performance models. Since it is not practicable to identify the best performance model in practice, this study clearly demonstrates that it is reliable to use the best fitted model for volatility forecasting. Also, in order to further validate the performance of the best fitted model, it was subjected to a historical back-test using Value at Risk (VaR) at 1% significance level. Although, no model clearly emerged as superior, it was indicated that an average loss of 1.2% is expected to be exceeded only 1% of the time. Moreover, volatility forecast from the back testing was relatively high during the first quarter of 2018 but however begun decreasing steadily with time.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML