E. O. Eze, U. E. Obasi, C. O. D. Udaya, F. Daniel
Department of Mathematics, Michael Okpara University of Agriculture, Umudike, Umuahia, Abia State, Nigeria
Correspondence to: E. O. Eze, Department of Mathematics, Michael Okpara University of Agriculture, Umudike, Umuahia, Abia State, Nigeria.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper is devoted to study the existence of periodic solution for a damped and forced Duffing oscillator using the Krasnoselskii’s fixed point theorem in Banach space. As an application, uniqueness and compactness of solution of Duffing oscillator was achieved using Gronwall’s Inequality and Eberlein Simultan theorem which extends some results in literature.
Keywords:
Krasnoselskii’s Fixed Point Theorem, Banach Space, Compactness, Analytic Semigroup, Duffing Oscillator
Cite this paper: E. O. Eze, U. E. Obasi, C. O. D. Udaya, F. Daniel, On the Krasnoselskii’s Fixed Point Theorem and the Existence of Periodic Solution for a Damped and Forced Duffing Oscillator, American Journal of Mathematics and Statistics, Vol. 9 No. 3, 2019, pp. 131-135. doi: 10.5923/j.ajms.20190903.03.
1. Introduction
The aim of this paper is to study existence of periodic solution for a damped and forced Duffing oscillator of the form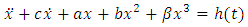 | (1.1) |
with boundary conditions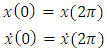 | (1.2) |
In equation (1.1) 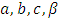 are real constants and
are real constants and 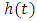 is continuous. Also,
is continuous. Also, 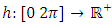 is periodic in
is periodic in 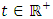 . Duffing oscillator is a second order nonlinear differential equation used to model dynamics of special types of mechanical and electrical systems. This differential equation has been named after the studies of Duffing in [1] which has a cubic nonlinearity and describes an oscillator. It is the simplest oscillator displaying catastrophic jumps of amplitude and phase when the frequency of the forcing term is taken as a gradually changing parameter. The main application have been in electronics and biology. For example, the brain is full of oscillators at micro and macro levels [2]. Several techniques have been used by many authors to study the existence of periodic solution of the Duffing type of equation (1.1) such as polar coordinates, the method of upper and lower solution, coincidence degree theory and a series of existence results of nontrivial solution of equation (1.1). We refer to [3-5] and reference therein. However, some methods of proving existence have some limitations and in fact for practical purposes serious difficulties arise frequently in the search for fixed point of Duffing equation with cubic nonlinearity.In this paper, we chose another strategy of proof which rely essentially on a fixed point theorem due to Krasnoselskii for a set that is closed, bounded and convex subset of a Banach space [6]. This result has been extensively employed in the related literature in the study of several kinds of separated boundary value problems (see for instance in [7, 8, 9, 10, 11] and their references); while for the periodic problem, it is more difficult to find references [12]. The reason for this contrast may be the fact that in order to apply this fixed point theorem, it is necessary to study the semigroup operator for linear equation, contraction and compactness of solution which are relatively difficult to study. To overcome this problem, Gronwalls inequality and Eberlein Simultian theorem were employed to obtain uniqueness and compactness of solution of Duffing equation.
. Duffing oscillator is a second order nonlinear differential equation used to model dynamics of special types of mechanical and electrical systems. This differential equation has been named after the studies of Duffing in [1] which has a cubic nonlinearity and describes an oscillator. It is the simplest oscillator displaying catastrophic jumps of amplitude and phase when the frequency of the forcing term is taken as a gradually changing parameter. The main application have been in electronics and biology. For example, the brain is full of oscillators at micro and macro levels [2]. Several techniques have been used by many authors to study the existence of periodic solution of the Duffing type of equation (1.1) such as polar coordinates, the method of upper and lower solution, coincidence degree theory and a series of existence results of nontrivial solution of equation (1.1). We refer to [3-5] and reference therein. However, some methods of proving existence have some limitations and in fact for practical purposes serious difficulties arise frequently in the search for fixed point of Duffing equation with cubic nonlinearity.In this paper, we chose another strategy of proof which rely essentially on a fixed point theorem due to Krasnoselskii for a set that is closed, bounded and convex subset of a Banach space [6]. This result has been extensively employed in the related literature in the study of several kinds of separated boundary value problems (see for instance in [7, 8, 9, 10, 11] and their references); while for the periodic problem, it is more difficult to find references [12]. The reason for this contrast may be the fact that in order to apply this fixed point theorem, it is necessary to study the semigroup operator for linear equation, contraction and compactness of solution which are relatively difficult to study. To overcome this problem, Gronwalls inequality and Eberlein Simultian theorem were employed to obtain uniqueness and compactness of solution of Duffing equation.
2. Preliminaries
Definition 2.1. (Boundedness of a function): A function 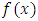 is bounded if
is bounded if 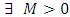
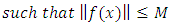
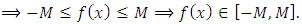 Definition 2.2. (Convex Set): Suppose X is a vector space. A subset
Definition 2.2. (Convex Set): Suppose X is a vector space. A subset 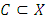 is said to be convex if whenever
is said to be convex if whenever 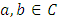 and
and 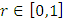 , it follows that
, it follows that 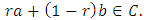 The closure of a set is again convex.Definition 2.3. (Hilbert Space): A pre-Hilbert space which is complete (considered as a normed linear space) is called Hilbert space.Definition 2.4. (Pre-Hilbert Space): A linear space X is said to be pre-Hilbert space if for every ordered pair of elements
The closure of a set is again convex.Definition 2.3. (Hilbert Space): A pre-Hilbert space which is complete (considered as a normed linear space) is called Hilbert space.Definition 2.4. (Pre-Hilbert Space): A linear space X is said to be pre-Hilbert space if for every ordered pair of elements 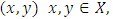 there is associated real number where X is a real linear space and complex number where X is a complex linear space such that
there is associated real number where X is a real linear space and complex number where X is a complex linear space such that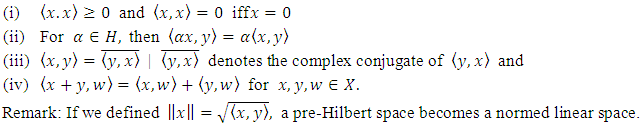 Definition 2.5. (Banach space): A normed linear space is called Banach space if it is complete in the sense of a metric given by the norm. Completeness means that every Cauchy sequence is convergent. Let
Definition 2.5. (Banach space): A normed linear space is called Banach space if it is complete in the sense of a metric given by the norm. Completeness means that every Cauchy sequence is convergent. Let 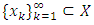 be any Cauchy sequence that is a sequence
be any Cauchy sequence that is a sequence 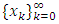 for which
for which 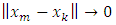 as
as 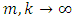 independently, then
independently, then 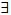 an element
an element 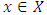 such that
such that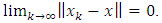 | (1.3) |
Definition 2.6. Let 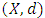 be a complete metric space. Then
be a complete metric space. Then 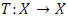 is called a contraction mapping if there exists a constant
is called a contraction mapping if there exists a constant 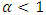 such that
such that 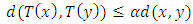 | (1.4) |
for each 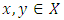 and where
and where 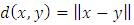 Theorem 2.9. (Contraction Mapping Principle) Let
Theorem 2.9. (Contraction Mapping Principle) Let 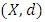 be a complete metric space and let
be a complete metric space and let 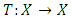 be a contraction, then T has a unique fixed point
be a contraction, then T has a unique fixed point 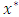 . Furthermore, for each
. Furthermore, for each 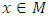
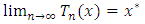 | (1.6) |
From this, one draws three conclusion in which this paper is written(i) T has a unique fixed point, say 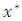 (ii) For each
(ii) For each 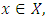 the picard sequence
the picard sequence 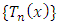 converges to
converges to 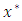 and also sequentially compact and converges to
and also sequentially compact and converges to 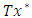 (iii) The convergence is uniform if X is bounded.Theorem 2.10. (Gronwalls-Bellman’s Inequality) Let f and g be continuous real-valued functions on some interval
(iii) The convergence is uniform if X is bounded.Theorem 2.10. (Gronwalls-Bellman’s Inequality) Let f and g be continuous real-valued functions on some interval 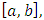 then
then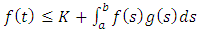 | (1.7) |
for some 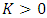 implies that
implies that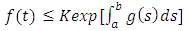 | (1.8) |
Proof. Multiplying both sides of equation (2.9) by 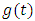 we have
we have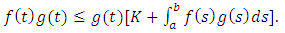 By hypothesis
By hypothesis 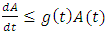 then
then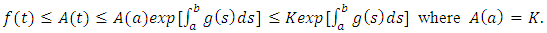 Hence,
Hence, 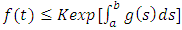 Remark: There is a generalization of this inequality. Its statement and proof is all about technicality.Definition 2.11. (Compactness) The subset A of a topological space X i.e
Remark: There is a generalization of this inequality. Its statement and proof is all about technicality.Definition 2.11. (Compactness) The subset A of a topological space X i.e 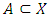 is said to be compact if every open cover of A has a finite subcover.Note: A subset
is said to be compact if every open cover of A has a finite subcover.Note: A subset 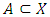 is pre-compact if
is pre-compact if 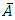 is compact.Definition 2.12. (Contraction Semigroup) Let E be a Banach space. A one-parameter family
is compact.Definition 2.12. (Contraction Semigroup) Let E be a Banach space. A one-parameter family 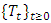 of bounded linear operators on E into itself is called a contraction semigroup of class
of bounded linear operators on E into itself is called a contraction semigroup of class 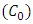 or simply a contraction semigroup if it satisfies the following conditions
or simply a contraction semigroup if it satisfies the following conditions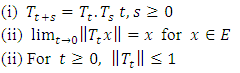 Note: (i) is called the semigroup property.Examples:(1)
Note: (i) is called the semigroup property.Examples:(1) 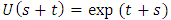 is a semigroup.(2) Let
is a semigroup.(2) Let 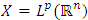 , with
, with 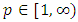 and
and 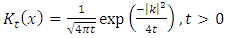 is a semigroup.Theorem 2.13.
is a semigroup.Theorem 2.13. 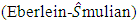 A subset of a Banach space X is relatively weak compact if only if it is relatively weakly sequentially compact. In particular, a subset of a Banach space X is weakly compact if and only if it is weakly sequentially compact.Theorem 2.14. (Krasnoselskii’s Fixed Point Theorem) Assume that F is a closed bounded convex subset of a Banach space X. Futhermore, assume that
A subset of a Banach space X is relatively weak compact if only if it is relatively weakly sequentially compact. In particular, a subset of a Banach space X is weakly compact if and only if it is weakly sequentially compact.Theorem 2.14. (Krasnoselskii’s Fixed Point Theorem) Assume that F is a closed bounded convex subset of a Banach space X. Futhermore, assume that 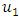 and
and 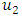 are mappings from F into X such that the following conditions hold:
are mappings from F into X such that the following conditions hold: Theorem 2.15. If
Theorem 2.15. If 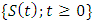 is a
is a 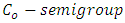 then
then 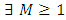 and
and 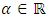 such that
such that 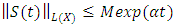 for each
for each 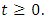 Proof: Since
Proof: Since 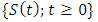 is continuous. Suppose by contraction, Let there exist a sequence
is continuous. Suppose by contraction, Let there exist a sequence 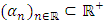 such that
such that 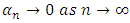 ,
, 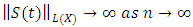 then by the uniform boundedness principle, there exist
then by the uniform boundedness principle, there exist 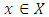 such that
such that 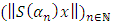 is unbounded contradicting the fact that
is unbounded contradicting the fact that 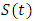 is continuous at
is continuous at 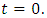
3. Main Result
We consider the Duffing equation of the form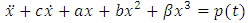 | (1.9) |
Equation (1.9) can be re-written in the following form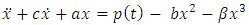 | (1.10) |
Vectorization of equation (1.10) is as followsLet 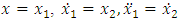 then equation (1.10) gives
then equation (1.10) gives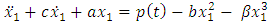 | (1.11) |
The equivalent system of equation (1.11) is given by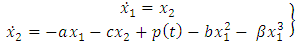 | (1.12) |
In matrix form equation (1.12) is written as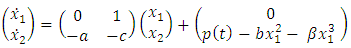 The above is of the form of non-autonomous equation given by
The above is of the form of non-autonomous equation given by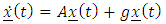 | (1.13) |
where 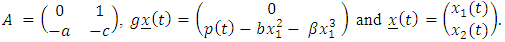 General solution of equation (1.13) is
General solution of equation (1.13) is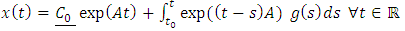 | (1.14) |
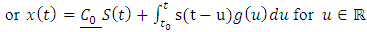 | (1.15) |
where 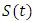 is a semigroup operator.To generate sequence of solutions in equation (1.14) we have that for
is a semigroup operator.To generate sequence of solutions in equation (1.14) we have that for 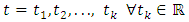 we have
we have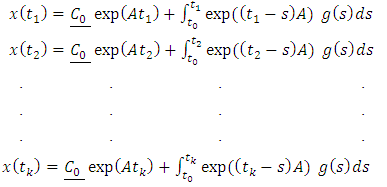 | (1.16) |
Now assuming that 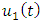 and
and 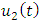 are solutions of equation (1.14) then we have that
are solutions of equation (1.14) then we have that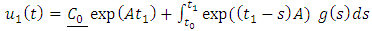 | (1.17) |
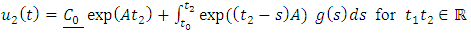 Furthermore, we will show that
Furthermore, we will show that 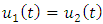 that is uniqueness.Suppose that
that is uniqueness.Suppose that 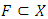 where X is a Banach space and F is a subspace and consider convexity of its solutions. For
where X is a Banach space and F is a subspace and consider convexity of its solutions. For 
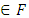 say, thenClaim 1:
say, thenClaim 1: 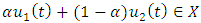 is convex,
is convex, 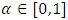 Proof: Case ITake
Proof: Case ITake 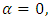 then 0.
then 0. 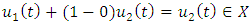 Case IITake
Case IITake 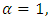 then
then 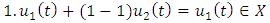 Case III, take
Case III, take 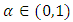 we have
we have 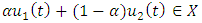
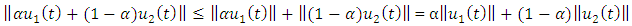
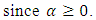 Claim 2: Is
Claim 2: Is 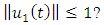 Proof:Define a ball,
Proof:Define a ball, 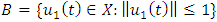 is convex. Then
is convex. Then 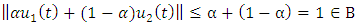 | (1.18) |
Hence the solution of the equation is convex.Next, we verified the boundedness property of our solution.Let 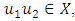 we show that
we show that 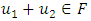
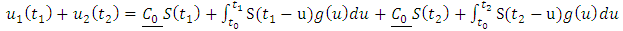 This is true by uniform boundedness principle. Applying theorem 2.15 we have
This is true by uniform boundedness principle. Applying theorem 2.15 we have 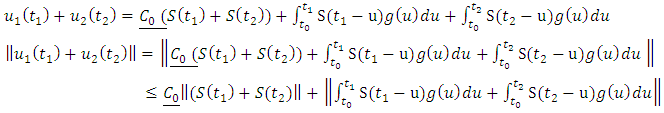 | (1.19) |
By semigroup property, 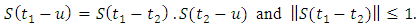 | (1.20) |
We have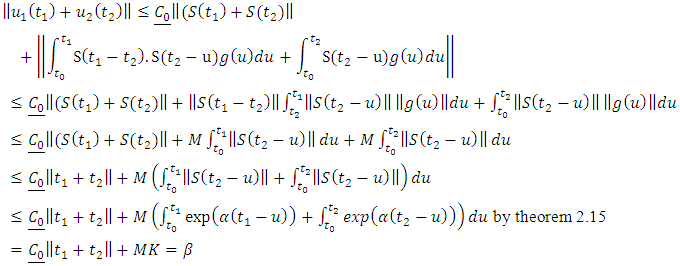 | (1.21) |
where 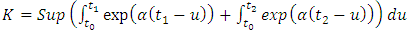
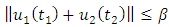 . So bounded for each
. So bounded for each 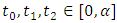 where
where 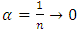 as
as 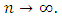 Next, we show that
Next, we show that 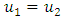 that is Uniqueness of Solution.But
that is Uniqueness of Solution.But 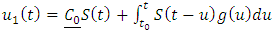 where
where 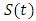 is a semigroup
is a semigroup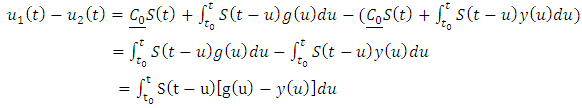 | (1.22) |
Hence,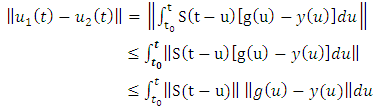 | (1.23) |
by theorem 2.15 and theorem 2.10 we have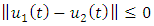 | (1.24) |
Therefore 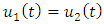 and since uniqueness of solution are satisfied, the closure is trivial. Hence
and since uniqueness of solution are satisfied, the closure is trivial. Hence 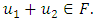 Furthermore, we will show that
Furthermore, we will show that 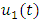 is a contraction that is
is a contraction that is 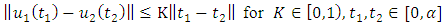 From equation (1.15) we have that
From equation (1.15) we have that 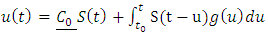 | (1.25) |
where 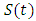 is a semigroup operator,
is a semigroup operator, 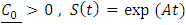 and
and 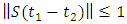 Claim: Equation (1.25) is a contractionProof:
Claim: Equation (1.25) is a contractionProof: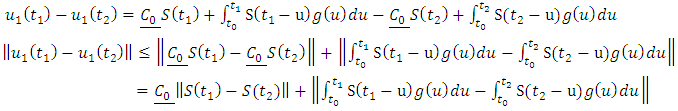 | (1.26) |
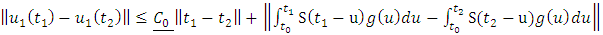 | (1.27) |
Using equation (1.20) which have the same idea with Banach-Mazur distance in supper multiplicative metric space we have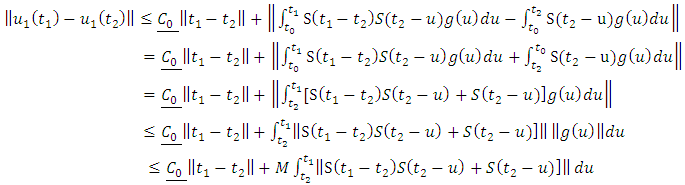 | (1.28) |
where 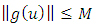 By theorem 2.15
By theorem 2.15 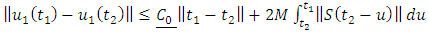 | (1.29) |
By theorem 2.10 equation (1.25) becomes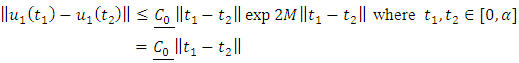
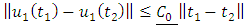 | (1.30) |
Now take 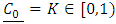 and equation (1.30) becomes
and equation (1.30) becomes 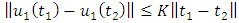 | (1.31) |
Hence equation (1.31) is a contraction.To show that 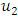 is a continuous, we proceeds as follows. Recall that
is a continuous, we proceeds as follows. Recall that 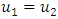 that is uniqueness of solution, then
that is uniqueness of solution, then 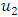 is also a contraction. Given any
is also a contraction. Given any 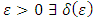 and
and 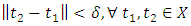 such that
such that 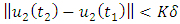 . If
. If 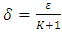 then
then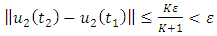 | (1.32) |
By equation (1.32) 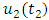 is continuous.Finally we use theorem 2.13 to establish the compactness of
is continuous.Finally we use theorem 2.13 to establish the compactness of 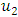 . Assume that we are in finite dimensional space, Hein-Borel guarantees our result that is since
. Assume that we are in finite dimensional space, Hein-Borel guarantees our result that is since 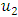 is closed and bounded hence compact. But since we are in infinite dimensional space (Banach space), by theorem 2.13,
is closed and bounded hence compact. But since we are in infinite dimensional space (Banach space), by theorem 2.13, 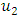 is sequentially compact hence compact. Therefore
is sequentially compact hence compact. Therefore 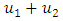 has a fixed point in F.
has a fixed point in F.
References
| [1] | I. Kovaic, M. J. Brennan, The Duffing equation: Nonlinear oscillators and their behavior, Wiley, (2011) 392. |
| [2] | E. C. Zeeman, Duffing equation in brain modelling, Bulletin of the institute of Mathematics and its applications, 12 (1976) 207-214. |
| [3] | F. I. Njoku, P. Omari, Stability properties of periodic solutions of a Duffing equation in the presence of lower and upper solutions, Application of Mathematics Computer, 135 (2003) 471-490. |
| [4] | Y. Lazer and K. Mckenna, Exact controllability of the suspension bridge model. Journal of Differential equation, 144 (1990) 66-98. |
| [5] | S. Chen-Li, K. Heing, Numerical characterization of the flow rectification of dynamic micro diffusers, Journal of Micro-mechanics and Micro-engineering, 16 (2007) 1331-1339. |
| [6] | H. L. Royden, P. M. Fitspatuik, Real Analysis, 4th edition, Pearson Education Asia Limited and Ghana Machine Press 2010. |
| [7] | M.A. Krasnosel’skii, Positive Solution of Operator Equations, Noordhoff, Groningen, 1964. |
| [8] | D. Guo, V. Laksmikantham, Multiple solution of two-point boundary value problems of ordinary differential equations in Banach spaces, Journal of Mathematical Analysis and Application, 129 (1988) 211-222. |
| [9] | E. Esmailzadeh, G. Nakhaie-Jazar, Periodic solution of a Mathieu-Duffing type equation, Journal of Nonlinear Mechanics, 32 (1997) 905-912. |
| [10] | J. Mawhin, Topological degree and boundary value problem for nonlinear differential equation in: M. Furi, P. Zecca (Eds.), Topological methods for ordinary differential equations, Lecture Notes in Mathematics, Vol. 1537, Springer, New York/Berlin, 1993, pp. 74-142. |
| [11] | P. Torres, Existence and uniqueness of elliptic periodic solution of the Brillouin electron beam focusing system, Journal of Maths Methods and Applied Sciences 23 (2000) 1139-1143. |
| [12] | P. J. Torres, Existence of one-signed periodic solution of some second order differential equations via a Krasnoselskii fixed point theorem, Journal of differential equations, 190 (2003) 643-662. |


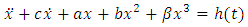
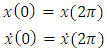
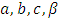 are real constants and
are real constants and 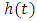 is continuous. Also,
is continuous. Also, 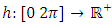 is periodic in
is periodic in 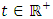 . Duffing oscillator is a second order nonlinear differential equation used to model dynamics of special types of mechanical and electrical systems. This differential equation has been named after the studies of Duffing in [1] which has a cubic nonlinearity and describes an oscillator. It is the simplest oscillator displaying catastrophic jumps of amplitude and phase when the frequency of the forcing term is taken as a gradually changing parameter. The main application have been in electronics and biology. For example, the brain is full of oscillators at micro and macro levels [2]. Several techniques have been used by many authors to study the existence of periodic solution of the Duffing type of equation (1.1) such as polar coordinates, the method of upper and lower solution, coincidence degree theory and a series of existence results of nontrivial solution of equation (1.1). We refer to [3-5] and reference therein. However, some methods of proving existence have some limitations and in fact for practical purposes serious difficulties arise frequently in the search for fixed point of Duffing equation with cubic nonlinearity.In this paper, we chose another strategy of proof which rely essentially on a fixed point theorem due to Krasnoselskii for a set that is closed, bounded and convex subset of a Banach space [6]. This result has been extensively employed in the related literature in the study of several kinds of separated boundary value problems (see for instance in [7, 8, 9, 10, 11] and their references); while for the periodic problem, it is more difficult to find references [12]. The reason for this contrast may be the fact that in order to apply this fixed point theorem, it is necessary to study the semigroup operator for linear equation, contraction and compactness of solution which are relatively difficult to study. To overcome this problem, Gronwalls inequality and Eberlein Simultian theorem were employed to obtain uniqueness and compactness of solution of Duffing equation.
. Duffing oscillator is a second order nonlinear differential equation used to model dynamics of special types of mechanical and electrical systems. This differential equation has been named after the studies of Duffing in [1] which has a cubic nonlinearity and describes an oscillator. It is the simplest oscillator displaying catastrophic jumps of amplitude and phase when the frequency of the forcing term is taken as a gradually changing parameter. The main application have been in electronics and biology. For example, the brain is full of oscillators at micro and macro levels [2]. Several techniques have been used by many authors to study the existence of periodic solution of the Duffing type of equation (1.1) such as polar coordinates, the method of upper and lower solution, coincidence degree theory and a series of existence results of nontrivial solution of equation (1.1). We refer to [3-5] and reference therein. However, some methods of proving existence have some limitations and in fact for practical purposes serious difficulties arise frequently in the search for fixed point of Duffing equation with cubic nonlinearity.In this paper, we chose another strategy of proof which rely essentially on a fixed point theorem due to Krasnoselskii for a set that is closed, bounded and convex subset of a Banach space [6]. This result has been extensively employed in the related literature in the study of several kinds of separated boundary value problems (see for instance in [7, 8, 9, 10, 11] and their references); while for the periodic problem, it is more difficult to find references [12]. The reason for this contrast may be the fact that in order to apply this fixed point theorem, it is necessary to study the semigroup operator for linear equation, contraction and compactness of solution which are relatively difficult to study. To overcome this problem, Gronwalls inequality and Eberlein Simultian theorem were employed to obtain uniqueness and compactness of solution of Duffing equation.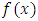 is bounded if
is bounded if 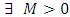
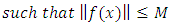
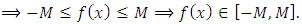 Definition 2.2. (Convex Set): Suppose X is a vector space. A subset
Definition 2.2. (Convex Set): Suppose X is a vector space. A subset 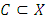 is said to be convex if whenever
is said to be convex if whenever 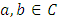 and
and 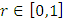 , it follows that
, it follows that 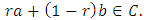 The closure of a set is again convex.Definition 2.3. (Hilbert Space): A pre-Hilbert space which is complete (considered as a normed linear space) is called Hilbert space.Definition 2.4. (Pre-Hilbert Space): A linear space X is said to be pre-Hilbert space if for every ordered pair of elements
The closure of a set is again convex.Definition 2.3. (Hilbert Space): A pre-Hilbert space which is complete (considered as a normed linear space) is called Hilbert space.Definition 2.4. (Pre-Hilbert Space): A linear space X is said to be pre-Hilbert space if for every ordered pair of elements 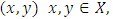 there is associated real number where X is a real linear space and complex number where X is a complex linear space such that
there is associated real number where X is a real linear space and complex number where X is a complex linear space such that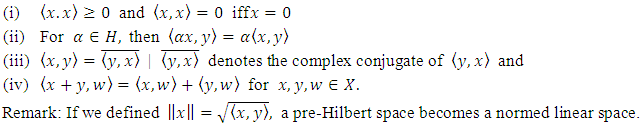 Definition 2.5. (Banach space): A normed linear space is called Banach space if it is complete in the sense of a metric given by the norm. Completeness means that every Cauchy sequence is convergent. Let
Definition 2.5. (Banach space): A normed linear space is called Banach space if it is complete in the sense of a metric given by the norm. Completeness means that every Cauchy sequence is convergent. Let 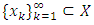 be any Cauchy sequence that is a sequence
be any Cauchy sequence that is a sequence 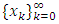 for which
for which 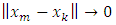 as
as 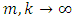 independently, then
independently, then 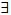 an element
an element 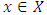 such that
such that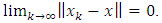
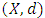 be a complete metric space. Then
be a complete metric space. Then 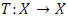 is called a contraction mapping if there exists a constant
is called a contraction mapping if there exists a constant 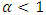 such that
such that 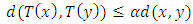
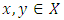 and where
and where 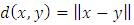 Theorem 2.9. (Contraction Mapping Principle) Let
Theorem 2.9. (Contraction Mapping Principle) Let 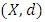 be a complete metric space and let
be a complete metric space and let 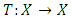 be a contraction, then T has a unique fixed point
be a contraction, then T has a unique fixed point 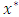 . Furthermore, for each
. Furthermore, for each 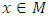
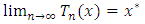
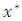 (ii) For each
(ii) For each 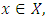 the picard sequence
the picard sequence 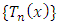 converges to
converges to 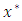 and also sequentially compact and converges to
and also sequentially compact and converges to 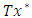 (iii) The convergence is uniform if X is bounded.Theorem 2.10. (Gronwalls-Bellman’s Inequality) Let f and g be continuous real-valued functions on some interval
(iii) The convergence is uniform if X is bounded.Theorem 2.10. (Gronwalls-Bellman’s Inequality) Let f and g be continuous real-valued functions on some interval 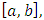 then
then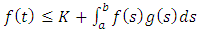
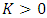 implies that
implies that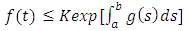
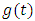 we have
we have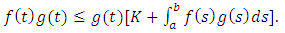 By hypothesis
By hypothesis 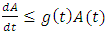 then
then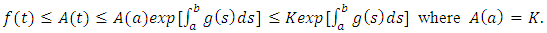 Hence,
Hence, 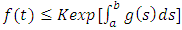 Remark: There is a generalization of this inequality. Its statement and proof is all about technicality.Definition 2.11. (Compactness) The subset A of a topological space X i.e
Remark: There is a generalization of this inequality. Its statement and proof is all about technicality.Definition 2.11. (Compactness) The subset A of a topological space X i.e 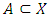 is said to be compact if every open cover of A has a finite subcover.Note: A subset
is said to be compact if every open cover of A has a finite subcover.Note: A subset 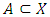 is pre-compact if
is pre-compact if 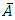 is compact.Definition 2.12. (Contraction Semigroup) Let E be a Banach space. A one-parameter family
is compact.Definition 2.12. (Contraction Semigroup) Let E be a Banach space. A one-parameter family 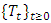 of bounded linear operators on E into itself is called a contraction semigroup of class
of bounded linear operators on E into itself is called a contraction semigroup of class 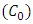 or simply a contraction semigroup if it satisfies the following conditions
or simply a contraction semigroup if it satisfies the following conditions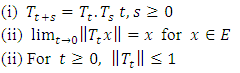 Note: (i) is called the semigroup property.Examples:(1)
Note: (i) is called the semigroup property.Examples:(1) 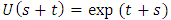 is a semigroup.(2) Let
is a semigroup.(2) Let 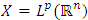 , with
, with 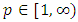 and
and 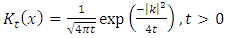 is a semigroup.Theorem 2.13.
is a semigroup.Theorem 2.13. 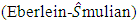 A subset of a Banach space X is relatively weak compact if only if it is relatively weakly sequentially compact. In particular, a subset of a Banach space X is weakly compact if and only if it is weakly sequentially compact.Theorem 2.14. (Krasnoselskii’s Fixed Point Theorem) Assume that F is a closed bounded convex subset of a Banach space X. Futhermore, assume that
A subset of a Banach space X is relatively weak compact if only if it is relatively weakly sequentially compact. In particular, a subset of a Banach space X is weakly compact if and only if it is weakly sequentially compact.Theorem 2.14. (Krasnoselskii’s Fixed Point Theorem) Assume that F is a closed bounded convex subset of a Banach space X. Futhermore, assume that 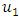 and
and 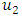 are mappings from F into X such that the following conditions hold:
are mappings from F into X such that the following conditions hold: Theorem 2.15. If
Theorem 2.15. If 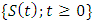 is a
is a 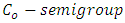 then
then 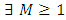 and
and 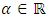 such that
such that 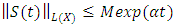 for each
for each 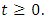 Proof: Since
Proof: Since 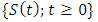 is continuous. Suppose by contraction, Let there exist a sequence
is continuous. Suppose by contraction, Let there exist a sequence 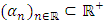 such that
such that 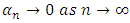 ,
, 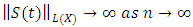 then by the uniform boundedness principle, there exist
then by the uniform boundedness principle, there exist 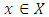 such that
such that 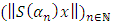 is unbounded contradicting the fact that
is unbounded contradicting the fact that 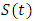 is continuous at
is continuous at 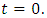
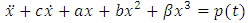
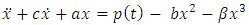
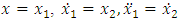 then equation (1.10) gives
then equation (1.10) gives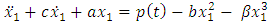
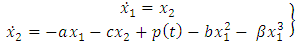
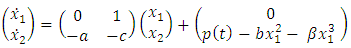 The above is of the form of non-autonomous equation given by
The above is of the form of non-autonomous equation given by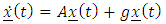
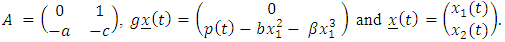 General solution of equation (1.13) is
General solution of equation (1.13) is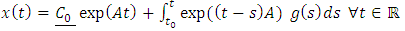
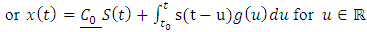
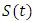 is a semigroup operator.To generate sequence of solutions in equation (1.14) we have that for
is a semigroup operator.To generate sequence of solutions in equation (1.14) we have that for 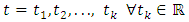 we have
we have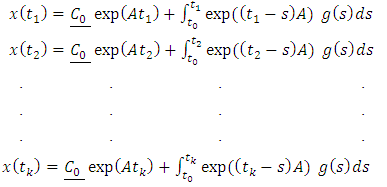
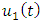 and
and 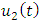 are solutions of equation (1.14) then we have that
are solutions of equation (1.14) then we have that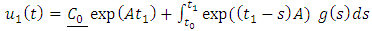
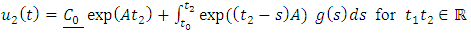 Furthermore, we will show that
Furthermore, we will show that 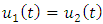 that is uniqueness.Suppose that
that is uniqueness.Suppose that 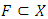 where X is a Banach space and F is a subspace and consider convexity of its solutions. For
where X is a Banach space and F is a subspace and consider convexity of its solutions. For 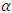
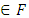 say, thenClaim 1:
say, thenClaim 1: 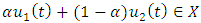 is convex,
is convex, 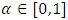 Proof: Case ITake
Proof: Case ITake 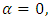 then 0.
then 0. 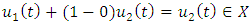 Case IITake
Case IITake 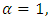 then
then 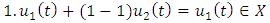 Case III, take
Case III, take 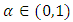 we have
we have 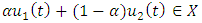
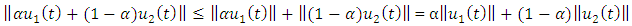
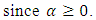 Claim 2: Is
Claim 2: Is 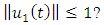 Proof:Define a ball,
Proof:Define a ball, 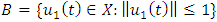 is convex. Then
is convex. Then 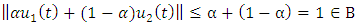
 we show that
we show that 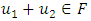
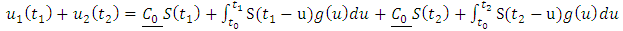 This is true by uniform boundedness principle. Applying theorem 2.15 we have
This is true by uniform boundedness principle. Applying theorem 2.15 we have 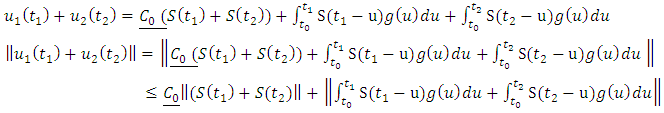
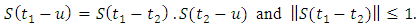
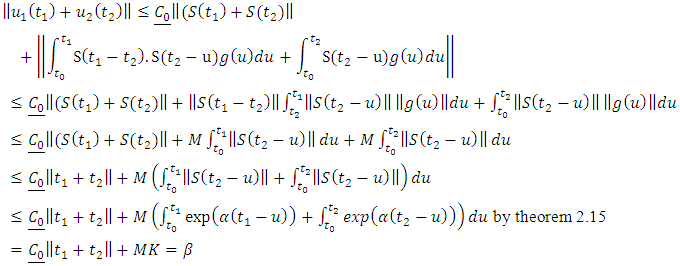
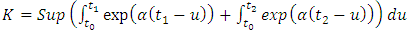
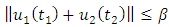 . So bounded for each
. So bounded for each 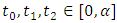 where
where 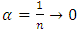 as
as 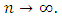 Next, we show that
Next, we show that 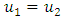 that is Uniqueness of Solution.But
that is Uniqueness of Solution.But 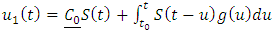 where
where 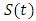 is a semigroup
is a semigroup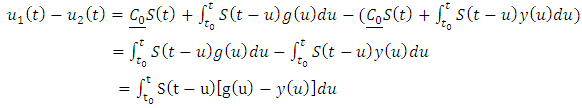
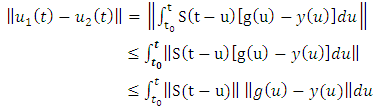
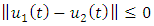
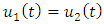 and since uniqueness of solution are satisfied, the closure is trivial. Hence
and since uniqueness of solution are satisfied, the closure is trivial. Hence 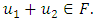 Furthermore, we will show that
Furthermore, we will show that 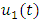 is a contraction that is
is a contraction that is 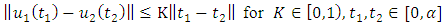 From equation (1.15) we have that
From equation (1.15) we have that 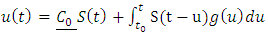
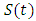 is a semigroup operator,
is a semigroup operator, 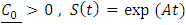 and
and 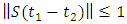 Claim: Equation (1.25) is a contractionProof:
Claim: Equation (1.25) is a contractionProof: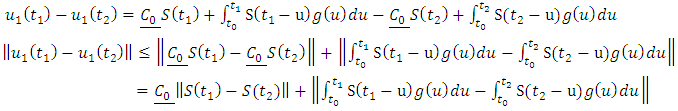
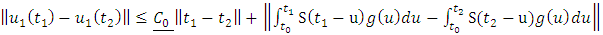
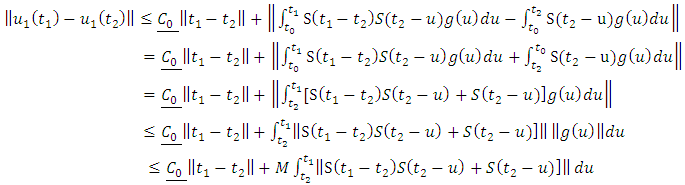
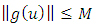 By theorem 2.15
By theorem 2.15 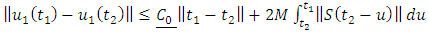
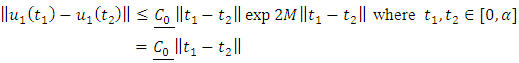
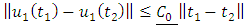
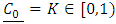 and equation (1.30) becomes
and equation (1.30) becomes 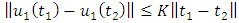
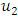 is a continuous, we proceeds as follows. Recall that
is a continuous, we proceeds as follows. Recall that 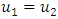 that is uniqueness of solution, then
that is uniqueness of solution, then 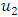 is also a contraction. Given any
is also a contraction. Given any 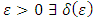 and
and 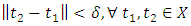 such that
such that 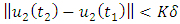 . If
. If 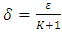 then
then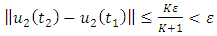
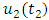 is continuous.Finally we use theorem 2.13 to establish the compactness of
is continuous.Finally we use theorem 2.13 to establish the compactness of 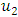 . Assume that we are in finite dimensional space, Hein-Borel guarantees our result that is since
. Assume that we are in finite dimensional space, Hein-Borel guarantees our result that is since 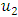 is closed and bounded hence compact. But since we are in infinite dimensional space (Banach space), by theorem 2.13,
is closed and bounded hence compact. But since we are in infinite dimensional space (Banach space), by theorem 2.13, 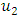 is sequentially compact hence compact. Therefore
is sequentially compact hence compact. Therefore 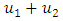 has a fixed point in F.
has a fixed point in F. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML