M. R. Hasan, A. R. Baizid
Department of Business Administration, Leading University, Sylhet, Bangladesh
Correspondence to: A. R. Baizid, Department of Business Administration, Leading University, Sylhet, Bangladesh.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, semi- minimax estimation of the scale parameter of Laplace distribution is presented by applying the theorem of Lehmann (1950) under symmetric (quadratic) and asymmetric (entropy and MLINEX) loss functions. The results of comparison among these estimators are compared empirically using R- Code simulation study with respect to the mean square error (MSE). In general, the result has showed that the semi- minimax estimator under MLINEX loss function is the best estimator with respect to MSE for all sample sizes. It has also observed that, MSE’s of the estimators is increasing with the increase of the scale parameter value. Finally, for all parameter values, an obvious reduction in MSE’s has observed with the increase in sample size.
Keywords:
Semi- minimax estimator, Laplace distribution, Bayes estimator, Quadratic loss function, Entropy loss function, MLINEX loss function
Cite this paper: M. R. Hasan, A. R. Baizid, Semi- Minimax Estimation of the Scale Parameter of Laplace Distribution under Symmetric and Asymmetric Loss Functions, American Journal of Mathematics and Statistics, Vol. 9 No. 3, 2019, pp. 123-130. doi: 10.5923/j.ajms.20190903.02.
1. Introduction
Semi- minimax estimation is an upgraded non- classical approach in the estimation area of statistical inference. The most important element in the Semi- minimax approach is the specification of the distribution function on the parameter space which is called prior distribution. In this paper we have studied the Semi- minimax estimators depend on the quadratic, entropy and MLINEX loss functions of the scale parameter of Laplace distribution. Al-kutubi and Ibrahim (2009) [1] compared Jeffrey prior and the extension of Jeffrey prior information for estimating the parameter of the exponential distribution. Asgharzadeh (2009) [2] Bayes estimators of the unknown parameter and the reliability function for the generalized exponential model has been derived under various loss functions such as the squared error, the absolute error, the squared log error, and the entropy loss functions. Dey (2008) [3] obtained Bayesian predictive intervals of the parameter of Rayleigh distribution. Amrollah (2011) [4] found the semi-minimax estimators of the scale parameter of the weibull distribution under quadratic and MLINEX loss functions. Masoud and Hassan (2010) [5] studied the minimax estimators of the shape parameter for the Burr type XII distribution under the squared log error, precautionary and weighted balanced squared error loss functions. Nassiri, Sajad and Hassan (2011) [6] studied the semi- minimax estimators of the parameter of the Rayleigh distribution for the well known quadratic and modified linear exponential loss functions and the efficiency of the estimators had also been studied. Podder (2004) [7] studied the minimax estimator of the Pareto distribution under quadratic and MLINEX loss functions. Also Shadrokh and Pazira (2010) [8] studied the minimax estimator for the minimax distribution under several loss functions. S. Ali et al [9] studied the scale parameter estimation of the Laplace model using different asymmetric loss functions for Laplace distribution. It is our interest to study the Semi- minimax estimation of the scale parameter of Laplace distribution for different symmetric and asymmetric loss functions to see the comparative situation. Since Laplace distribution is used in hydrology to extreme events such as annual maximum one- day rainfall and river discharges. This distribution has also been used in speech recognition to model priors on discrete Furrier transform (DFT) coefficients and in joint photographic experts group (JPEG) image compression to model AC coefficients generated by a discrete cosine transform (DCT) [10].Laplace distribution is a continuous probability distribution. It has generally two parameters. One is location parameter 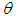 and other is scale parameter
and other is scale parameter 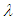 . Practically location parameter has limited use. Here only scale parameter is considered to estimate. A continuous random variable X is said to have Laplace
. Practically location parameter has limited use. Here only scale parameter is considered to estimate. A continuous random variable X is said to have Laplace 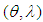 distribution if its probability density function (pdf) is given by [11]
distribution if its probability density function (pdf) is given by [11] 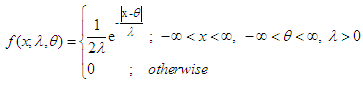 | (1) |
where, 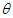 is the location parameter and
is the location parameter and 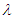 is the scale parameter. The cumulative distribution function (cdf) of Laplace distribution is given by
is the scale parameter. The cumulative distribution function (cdf) of Laplace distribution is given by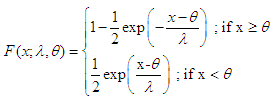
2. Prior and Posterior Density Function of Parameter 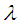
Let us assume that 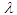 has Inverse gamma prior distribution is [4] defined as
has Inverse gamma prior distribution is [4] defined as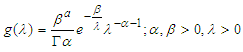 Then the posterior distribution of
Then the posterior distribution of 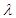 for the given random sample
for the given random sample 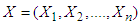 is given by
is given by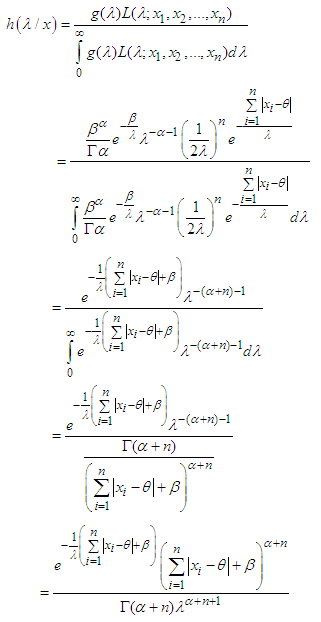 | (2) |
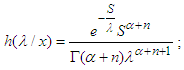 Here,
Here, 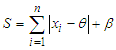 This implies that, the posterior density is recognized as the density of the Inverse Gamma (IG) distribution:
This implies that, the posterior density is recognized as the density of the Inverse Gamma (IG) distribution: 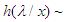
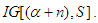 We have applied Lehmann’s Theorem [12] in our article. Lehmann’s Theorem states: Let
We have applied Lehmann’s Theorem [12] in our article. Lehmann’s Theorem states: Let 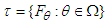 be a family of distribution function and D be a class of estimators of θ. Suppose, that
be a family of distribution function and D be a class of estimators of θ. Suppose, that 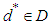 is a Baye’s estimator against a prior distribution
is a Baye’s estimator against a prior distribution 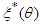 on the parameter space Ω, and the risk function
on the parameter space Ω, and the risk function 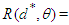 constant on Ω, then
constant on Ω, then 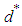 is a minimax estimator of θ.
is a minimax estimator of θ.
3. Bayes Estimator of Parameter 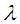 under Quadratic Loss Function
under Quadratic Loss Function
We consider the quadratic loss function [3] of the form 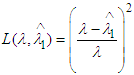 .Then the Bayes estimator of λ for the above loss function is given by
.Then the Bayes estimator of λ for the above loss function is given by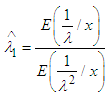 | (3) |
Now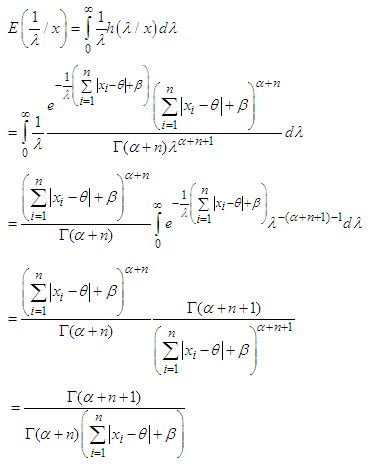 | (4) |
Similarly, 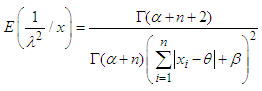 | (5) |
Substituting (4) and (5) in (3) we get, 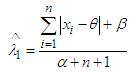 Hence,
Hence, 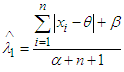 is the Bayes estimator under quadratic loss function. Now the risk function [3] of the estimator
is the Bayes estimator under quadratic loss function. Now the risk function [3] of the estimator 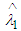 is
is 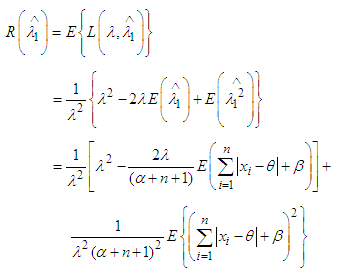 Let,
Let, 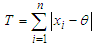 , such that the statistic T is distributed as
, such that the statistic T is distributed as 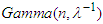
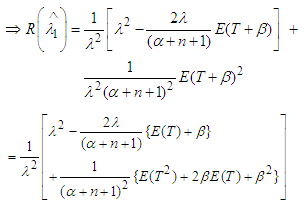 | (6) |
Since, 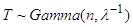 hence
hence  ,
, 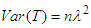 ,
, 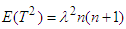
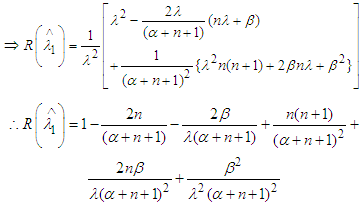 | (7) |
From (7) it is clear that 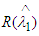 is not constant. So
is not constant. So 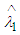 is not minimax estimator exactly. Now return to (6) and let β→0, we get.
is not minimax estimator exactly. Now return to (6) and let β→0, we get.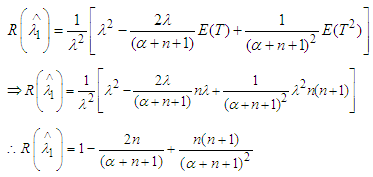 Which is independent of λ, hence according to the Lehmann’s theorem it follows that
Which is independent of λ, hence according to the Lehmann’s theorem it follows that 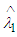 is the semi- minimax estimator for the parameter λ.
is the semi- minimax estimator for the parameter λ.
4. Bayes Estimator of Parameter 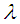 under Entropy Loss Function
under Entropy Loss Function
Let us consider the entropy loss function [2] of the form: 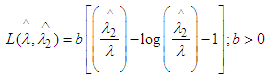 Then the Bayes estimator of λ for the above loss functionis given by:
Then the Bayes estimator of λ for the above loss functionis given by: 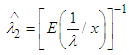 From (4) we get,
From (4) we get,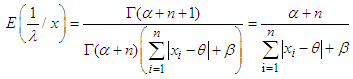 Hence,
Hence, 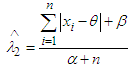 is the Bayes estimator under entropy loss function. Now the risk function [2] of the estimator
is the Bayes estimator under entropy loss function. Now the risk function [2] of the estimator 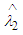 is
is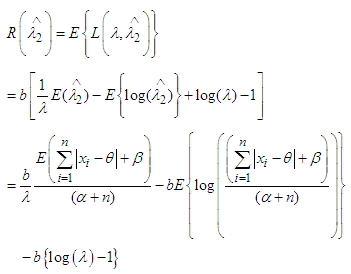 After simplification we can write
After simplification we can write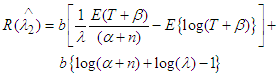 | (8) |
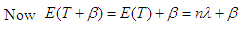 | (9) |
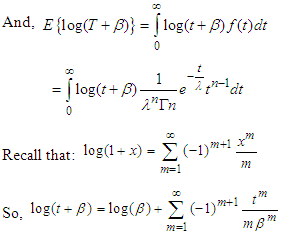
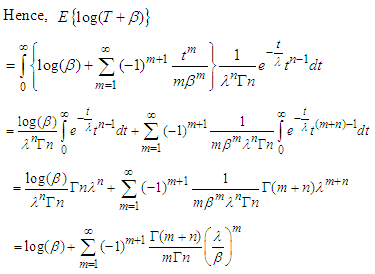 | (10) |
Substituting (9) and (10) in (8) we get,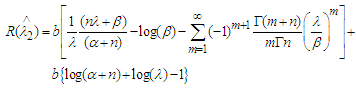 | (11) |
From (11) it is clear that 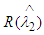 is not constant. So
is not constant. So 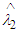 is not minimax estimator exactly. Now return to (8) and let β→0, we get.
is not minimax estimator exactly. Now return to (8) and let β→0, we get.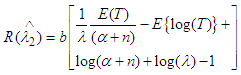 | (12) |
Now, 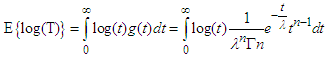 Let,
Let, 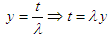 So,
So, 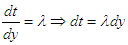
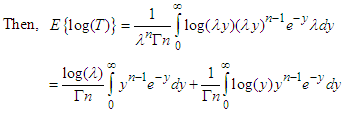
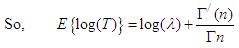 | (13) |
Here, 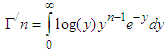 is the first derivative of
is the first derivative of 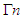 with respect to n. Substituting the value of E(T) and
with respect to n. Substituting the value of E(T) and 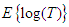 in (12) we get
in (12) we get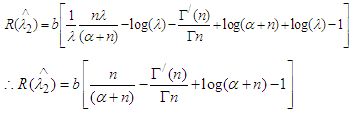 Which is independent of λ, hence according to the Lehmann’s theorem it follows that
Which is independent of λ, hence according to the Lehmann’s theorem it follows that 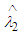 is the semi- minimax estimator for the parameter λ.
is the semi- minimax estimator for the parameter λ.
5. Bayes Estimator of Parameter 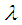 under MLINEX Loss Function
under MLINEX Loss Function
Let, the MLINEX loss function [4] is defined as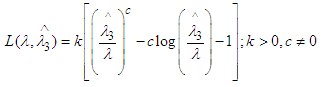 Then the Bayes estimator of λ for the above loss function is given by
Then the Bayes estimator of λ for the above loss function is given by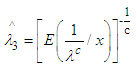 | (14) |
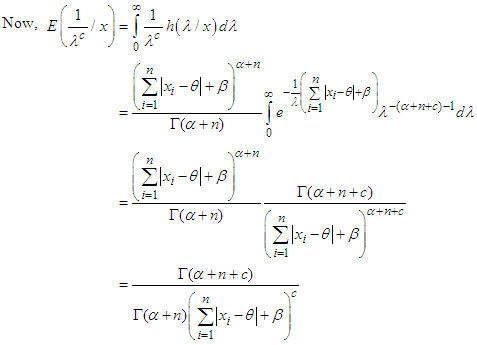 From equation (14) we get,
From equation (14) we get,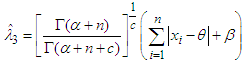 Hence,
Hence, 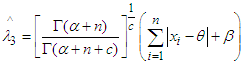 is the Bayes estimator under MLINEX loss function.Now the risk function [4] of the estimator
is the Bayes estimator under MLINEX loss function.Now the risk function [4] of the estimator 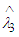 is
is 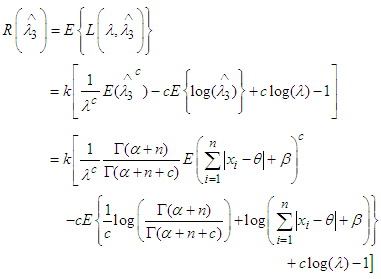
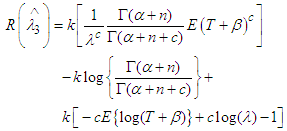 | (15) |
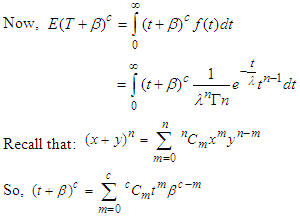
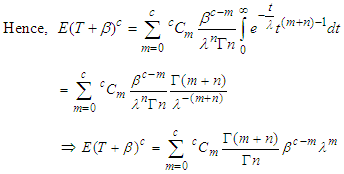 | (16) |
Substituting (10) and (16) in (15) we get,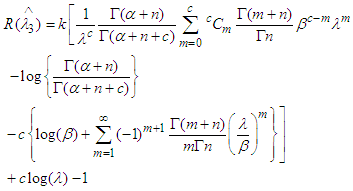 | (17) |
From (17) it is clear that 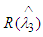 is not constant. So
is not constant. So 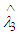 is not minimax estimator exactly. Now return to (14) and let β→0, we get.
is not minimax estimator exactly. Now return to (14) and let β→0, we get.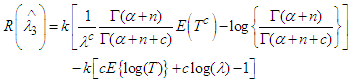 | (18) |
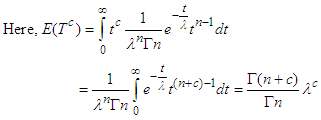 | (19) |
Substituting (13) and (19) in (18) we get,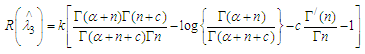 Which is independent of λ, hence according to the Lehmann’s theorem it follows that
Which is independent of λ, hence according to the Lehmann’s theorem it follows that 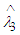 is the semi- minimax estimator for the parameter λ.
is the semi- minimax estimator for the parameter λ.
6. Empirical Analysis
The estimated value and MSE of the different estimators of the scale parameter 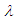 are computed by R- Code from the Laplace distribution, where
are computed by R- Code from the Laplace distribution, where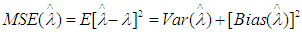 In the simulation study, we have chosen n= 5, 15, 25, 35 and 50 for several values of c= -1, 1, 2, also for λ= 1, 3; θ= 0.5, 1, 1.5, 2, -0.5, -1, -1.5, -2; α= 0.2, 1.2, 1.5 and β= 0.3, 0.5, all results are based on simulations (S= 3000). The results have summarized and tabulated in the following tables for each estimated value (EV) of the estimators and for all sample sizes (n) where C is for Criteria.
In the simulation study, we have chosen n= 5, 15, 25, 35 and 50 for several values of c= -1, 1, 2, also for λ= 1, 3; θ= 0.5, 1, 1.5, 2, -0.5, -1, -1.5, -2; α= 0.2, 1.2, 1.5 and β= 0.3, 0.5, all results are based on simulations (S= 3000). The results have summarized and tabulated in the following tables for each estimated value (EV) of the estimators and for all sample sizes (n) where C is for Criteria.
7. Conclusions
The results of the simulation study for estimating the semi- minimax estimator of the scale parameter 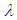 of Laplace distribution when the location parameter
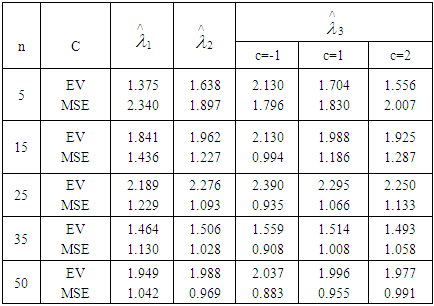
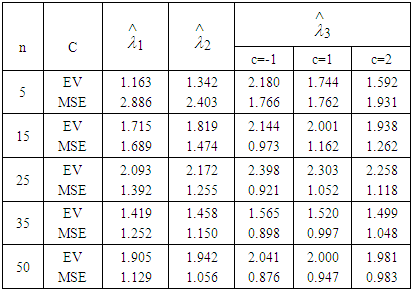
of Laplace distribution when the location parameter 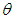 is known are summarized and tabulated in above tables which contain the estimated value and MSE’s we have observed. In the most cases, the results in table 1 to 8 have showed that the semi- minimax estimator under MLINEX loss function has the smallest MSE. That means this estimator is better than other estimators with different sample sizes. Table (1, 2, 3, 4, 6 and 8) shows that for n= 5, the semi- minimax estimator under MLINEX loss function has smallest MSE for c= 1. But for n≥ 15, this estimator has smallest MSE for c= -1 and this is also smallest among all estimators. Also table (5 and 7) shows that for different sample sizes, the semi- minimax estimator under MLINEX loss function has smallest MSE for c= -1.
is known are summarized and tabulated in above tables which contain the estimated value and MSE’s we have observed. In the most cases, the results in table 1 to 8 have showed that the semi- minimax estimator under MLINEX loss function has the smallest MSE. That means this estimator is better than other estimators with different sample sizes. Table (1, 2, 3, 4, 6 and 8) shows that for n= 5, the semi- minimax estimator under MLINEX loss function has smallest MSE for c= 1. But for n≥ 15, this estimator has smallest MSE for c= -1 and this is also smallest among all estimators. Also table (5 and 7) shows that for different sample sizes, the semi- minimax estimator under MLINEX loss function has smallest MSE for c= -1.Table 1. Estimated Value and MSE of Different Estimators of Parameter
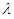 of Laplace Distribution for Different Values of n When of Laplace Distribution for Different Values of n When
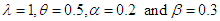
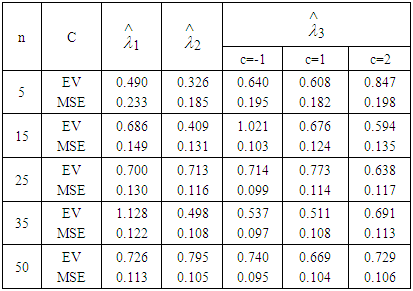 |
| |
|
Table 2. Estimated Value and MSE of Different Estimators of Parameter
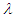 of Laplace Distribution for Different Values of n When of Laplace Distribution for Different Values of n When
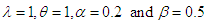
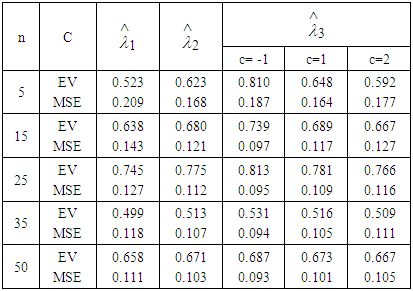 |
| |
|
Table 3. Estimated Value and MSE of Different Estimators of Parameter
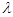 of Laplace Distribution for Different Values of n When of Laplace Distribution for Different Values of n When
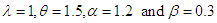
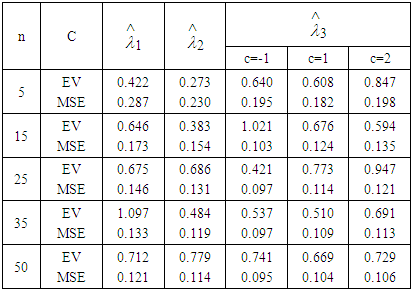 |
| |
|
Table 4. Estimated Value and MSE of Different Estimators of Parameter
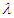 of Laplace Distribution for Different Values of n When of Laplace Distribution for Different Values of n When
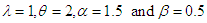
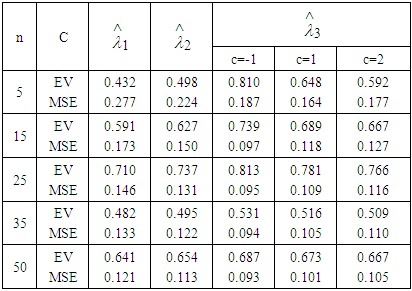 |
| |
|
Table 5. Estimated value and MSE of different estimators of parameter
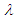 of Laplace distribution for different values of n when of Laplace distribution for different values of n when
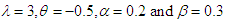
 |
| |
|
Table 6. Estimated Value and MSE of Different Estimators of Parameter
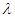 of Laplace Distribution for Different Values of n When of Laplace Distribution for Different Values of n When
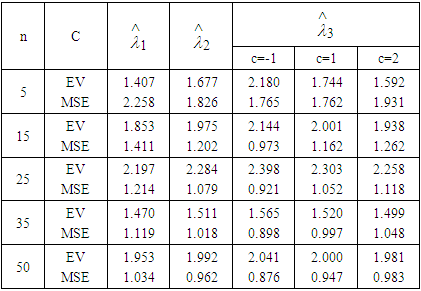 |
| |
|
Table 7. Estimated Value and MSE of Different Estimators of Parameter
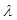 of Laplace Distribution for Different Values of n When of Laplace Distribution for Different Values of n When
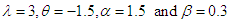
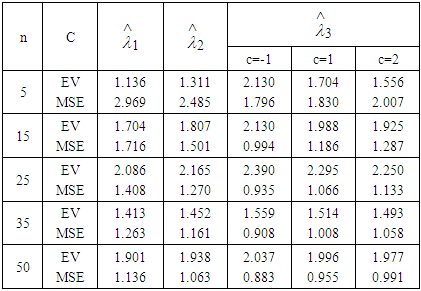 |
| |
|
Table 8. Estimated Value and MSE of Different Estimators of Parameter
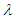 of Laplace Distribution for Different Values of n When of Laplace Distribution for Different Values of n When
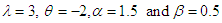
 |
| |
|
It has observed that, MSE’s of estimators of scale parameter is increasing with the increase of the scale parameter value. It has also observed that the MSE’s of different estimators of scale parameter 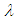 decreases with increasing the sample sizes which matches with the result of S. Ali et al [9]. Finally, for all parameter values, an obvious reduction in MSE’s has observed with the increase in sample size. We can apply our study in calculating annual maximum one- day rainfall and river discharges, to model priors on discrete Furrier transform (DFT) coefficients and AC coefficients generated by a discrete cosine transform.
decreases with increasing the sample sizes which matches with the result of S. Ali et al [9]. Finally, for all parameter values, an obvious reduction in MSE’s has observed with the increase in sample size. We can apply our study in calculating annual maximum one- day rainfall and river discharges, to model priors on discrete Furrier transform (DFT) coefficients and AC coefficients generated by a discrete cosine transform.
References
| [1] | Al-kutubi, H. S., and Ibrahim, N. A., (2009) ''Baye’s estimator for Exponential distribution with extension of Jeffrey prior information'', Malaysian Journal of mathematical sciences, Vol. 3, pp. 297-313. |
| [2] | Asgharzadeh, A., and Rezaei, R., (2009) ''The generalized exponential distribution as a life time model under different loss functions'', Data science journal, Vol. 8. |
| [3] | Dey, S., (2008) ''Minimax estimation of parameter of the Rayleigh distribution under quadratic loss function'', Data science Journal, Vol. 7 pp. 23-31. |
| [4] | Jafari, and Amrollah, (2011) ''Semi-Minimax estimations on the Weibull distribution'', Int. J. of Academic Research, Vol. 3, pp. 169-176. |
| [5] | Masoud, Y., and Hassan, P., (2010) ''Minimax estimation of the parameter of the Burr type Xii distribution'', Australian journal of Basic and applied sciences, Vol. 4, No. 12. |
| [6] | Nasiri, P., Sajad, G., and Hassan, P., (2011) ''Semi-Minimax estimation of the parameter of the Rayleigh distribution’’, Int. J. of Academic Research, Vol. 3, pp. 153-161. |
| [7] | Podder, C. K., Roy, M. K., Bhuyan, K. J., and Karim, A., (2004) ''Minimax estimation of the parameter of the Pareto distribution for quadratic and MLINEX loss functions'', Pak. J. statistics, Vol. 20, pp. 137-149. |
| [8] | Shadrokh, A., and Pazira, H., (2010) ''Minimax estimation on the minimax distribution'', Int. J. statist. Syst. Vol. 5, pp. 99-118. |
| [9] | Ali S., Aslam M., Abbas N., and Kazmi S.M.A. (2012) “The scale parameter estimation of the Laplace model using different asymmetric loss functions distribution”, International Journal of Statistics and Probability, Vol-1, No. -1. pp. 111. |
| [10] | https://en.wikipedia.org/wiki/Laplace_distribution#Applications. |
| [11] | https://en.wikipedia.org/wiki/Laplace_distribution#Probability_density_function. |
| [12] | Hodge, Z. I., and Lehmann, E. L., (1950) ''Some problem in minimax estimation'', Annals math. Statistics. Vol. 21, pp. 182-197. |



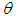 and other is scale parameter
and other is scale parameter 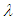 . Practically location parameter has limited use. Here only scale parameter is considered to estimate. A continuous random variable X is said to have Laplace
. Practically location parameter has limited use. Here only scale parameter is considered to estimate. A continuous random variable X is said to have Laplace 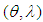 distribution if its probability density function (pdf) is given by [11]
distribution if its probability density function (pdf) is given by [11] 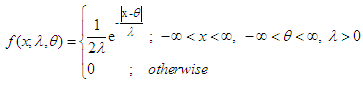
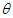 is the location parameter and
is the location parameter and 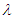 is the scale parameter. The cumulative distribution function (cdf) of Laplace distribution is given by
is the scale parameter. The cumulative distribution function (cdf) of Laplace distribution is given by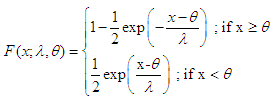
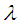
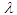 has Inverse gamma prior distribution is [4] defined as
has Inverse gamma prior distribution is [4] defined as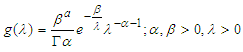 Then the posterior distribution of
Then the posterior distribution of 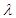 for the given random sample
for the given random sample 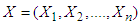 is given by
is given by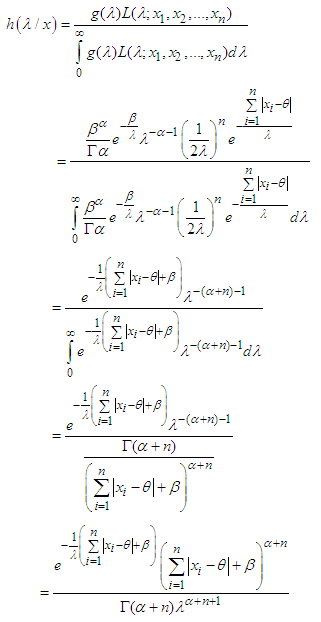
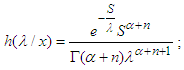 Here,
Here, 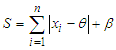 This implies that, the posterior density is recognized as the density of the Inverse Gamma (IG) distribution:
This implies that, the posterior density is recognized as the density of the Inverse Gamma (IG) distribution: 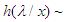
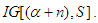 We have applied Lehmann’s Theorem [12] in our article. Lehmann’s Theorem states: Let
We have applied Lehmann’s Theorem [12] in our article. Lehmann’s Theorem states: Let 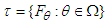 be a family of distribution function and D be a class of estimators of θ. Suppose, that
be a family of distribution function and D be a class of estimators of θ. Suppose, that 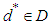 is a Baye’s estimator against a prior distribution
is a Baye’s estimator against a prior distribution 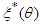 on the parameter space Ω, and the risk function
on the parameter space Ω, and the risk function 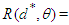 constant on Ω, then
constant on Ω, then 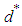 is a minimax estimator of θ.
is a minimax estimator of θ.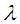 under Quadratic Loss Function
under Quadratic Loss Function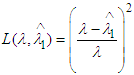 .Then the Bayes estimator of λ for the above loss function is given by
.Then the Bayes estimator of λ for the above loss function is given by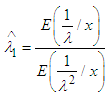
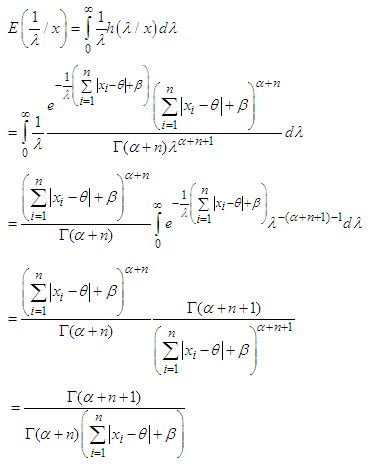
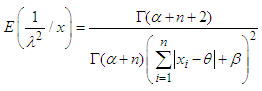
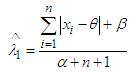 Hence,
Hence, 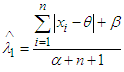 is the Bayes estimator under quadratic loss function. Now the risk function [3] of the estimator
is the Bayes estimator under quadratic loss function. Now the risk function [3] of the estimator 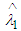 is
is 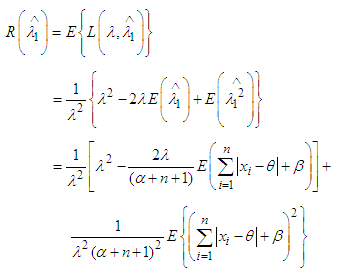 Let,
Let, 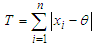 , such that the statistic T is distributed as
, such that the statistic T is distributed as 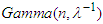
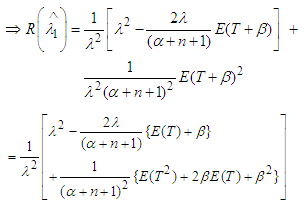
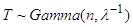 hence
hence  ,
, 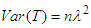 ,
, 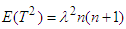
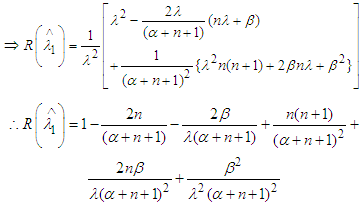
 is not constant. So
is not constant. So  is not minimax estimator exactly. Now return to (6) and let β→0, we get.
is not minimax estimator exactly. Now return to (6) and let β→0, we get.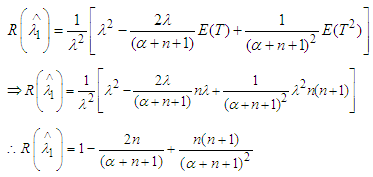 Which is independent of λ, hence according to the Lehmann’s theorem it follows that
Which is independent of λ, hence according to the Lehmann’s theorem it follows that 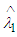 is the semi- minimax estimator for the parameter λ.
is the semi- minimax estimator for the parameter λ.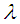 under Entropy Loss Function
under Entropy Loss Function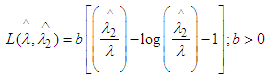 Then the Bayes estimator of λ for the above loss functionis given by:
Then the Bayes estimator of λ for the above loss functionis given by: 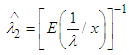 From (4) we get,
From (4) we get,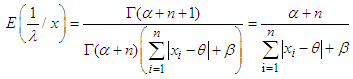 Hence,
Hence, 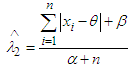 is the Bayes estimator under entropy loss function. Now the risk function [2] of the estimator
is the Bayes estimator under entropy loss function. Now the risk function [2] of the estimator 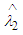 is
is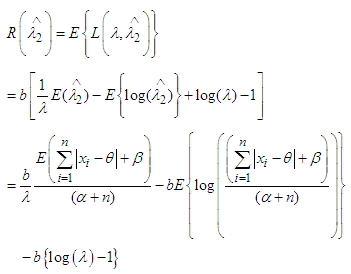 After simplification we can write
After simplification we can write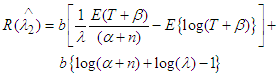
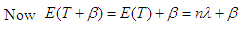
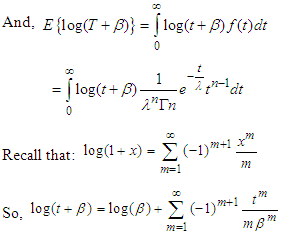
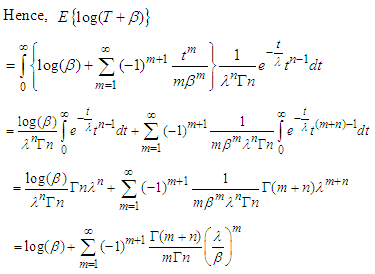
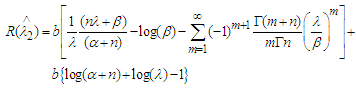
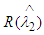 is not constant. So
is not constant. So 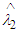 is not minimax estimator exactly. Now return to (8) and let β→0, we get.
is not minimax estimator exactly. Now return to (8) and let β→0, we get.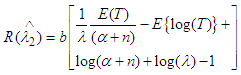
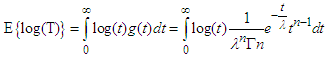 Let,
Let, 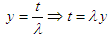 So,
So, 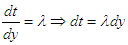
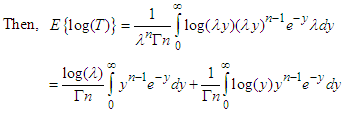
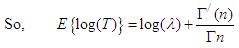
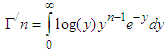 is the first derivative of
is the first derivative of 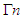 with respect to n. Substituting the value of E(T) and
with respect to n. Substituting the value of E(T) and 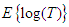 in (12) we get
in (12) we get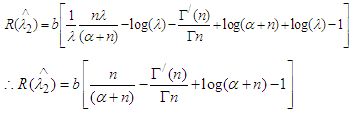 Which is independent of λ, hence according to the Lehmann’s theorem it follows that
Which is independent of λ, hence according to the Lehmann’s theorem it follows that 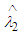 is the semi- minimax estimator for the parameter λ.
is the semi- minimax estimator for the parameter λ. under MLINEX Loss Function
under MLINEX Loss Function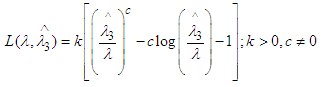 Then the Bayes estimator of λ for the above loss function is given by
Then the Bayes estimator of λ for the above loss function is given by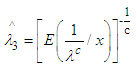
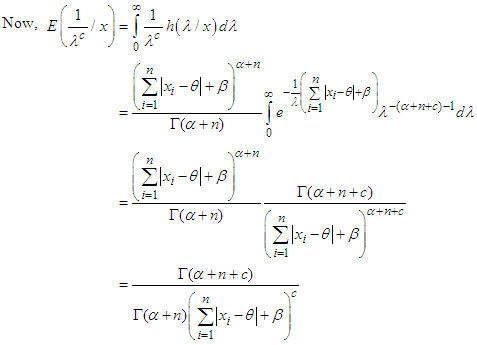 From equation (14) we get,
From equation (14) we get,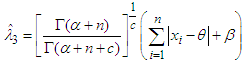 Hence,
Hence, 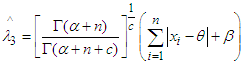 is the Bayes estimator under MLINEX loss function.Now the risk function [4] of the estimator
is the Bayes estimator under MLINEX loss function.Now the risk function [4] of the estimator 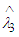 is
is 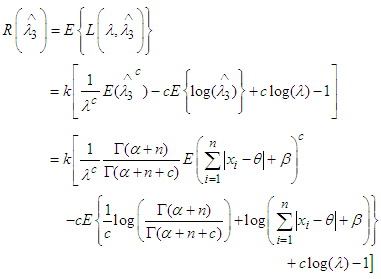
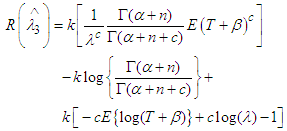
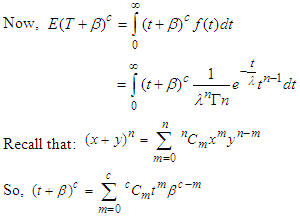
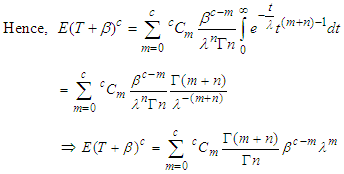
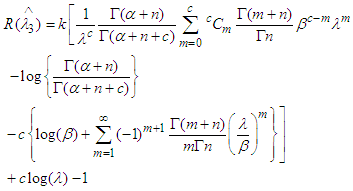
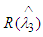 is not constant. So
is not constant. So 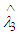 is not minimax estimator exactly. Now return to (14) and let β→0, we get.
is not minimax estimator exactly. Now return to (14) and let β→0, we get.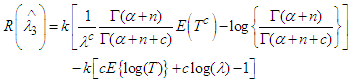
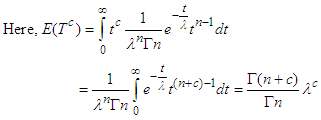
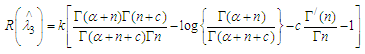 Which is independent of λ, hence according to the Lehmann’s theorem it follows that
Which is independent of λ, hence according to the Lehmann’s theorem it follows that 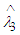 is the semi- minimax estimator for the parameter λ.
is the semi- minimax estimator for the parameter λ.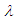 are computed by R- Code from the Laplace distribution, where
are computed by R- Code from the Laplace distribution, where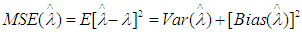 In the simulation study, we have chosen n= 5, 15, 25, 35 and 50 for several values of c= -1, 1, 2, also for λ= 1, 3; θ= 0.5, 1, 1.5, 2, -0.5, -1, -1.5, -2; α= 0.2, 1.2, 1.5 and β= 0.3, 0.5, all results are based on simulations (S= 3000). The results have summarized and tabulated in the following tables for each estimated value (EV) of the estimators and for all sample sizes (n) where C is for Criteria.
In the simulation study, we have chosen n= 5, 15, 25, 35 and 50 for several values of c= -1, 1, 2, also for λ= 1, 3; θ= 0.5, 1, 1.5, 2, -0.5, -1, -1.5, -2; α= 0.2, 1.2, 1.5 and β= 0.3, 0.5, all results are based on simulations (S= 3000). The results have summarized and tabulated in the following tables for each estimated value (EV) of the estimators and for all sample sizes (n) where C is for Criteria. 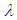 of Laplace distribution when the location parameter
of Laplace distribution when the location parameter 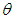 is known are summarized and tabulated in above tables which contain the estimated value and MSE’s we have observed. In the most cases, the results in table 1 to 8 have showed that the semi- minimax estimator under MLINEX loss function has the smallest MSE. That means this estimator is better than other estimators with different sample sizes. Table (1, 2, 3, 4, 6 and 8) shows that for n= 5, the semi- minimax estimator under MLINEX loss function has smallest MSE for c= 1. But for n≥ 15, this estimator has smallest MSE for c= -1 and this is also smallest among all estimators. Also table (5 and 7) shows that for different sample sizes, the semi- minimax estimator under MLINEX loss function has smallest MSE for c= -1.
is known are summarized and tabulated in above tables which contain the estimated value and MSE’s we have observed. In the most cases, the results in table 1 to 8 have showed that the semi- minimax estimator under MLINEX loss function has the smallest MSE. That means this estimator is better than other estimators with different sample sizes. Table (1, 2, 3, 4, 6 and 8) shows that for n= 5, the semi- minimax estimator under MLINEX loss function has smallest MSE for c= 1. But for n≥ 15, this estimator has smallest MSE for c= -1 and this is also smallest among all estimators. Also table (5 and 7) shows that for different sample sizes, the semi- minimax estimator under MLINEX loss function has smallest MSE for c= -1.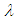 decreases with increasing the sample sizes which matches with the result of S. Ali et al [9]. Finally, for all parameter values, an obvious reduction in MSE’s has observed with the increase in sample size. We can apply our study in calculating annual maximum one- day rainfall and river discharges, to model priors on discrete Furrier transform (DFT) coefficients and AC coefficients generated by a discrete cosine transform.
decreases with increasing the sample sizes which matches with the result of S. Ali et al [9]. Finally, for all parameter values, an obvious reduction in MSE’s has observed with the increase in sample size. We can apply our study in calculating annual maximum one- day rainfall and river discharges, to model priors on discrete Furrier transform (DFT) coefficients and AC coefficients generated by a discrete cosine transform. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML of Laplace Distribution for Different Values of n When
of Laplace Distribution for Different Values of n When 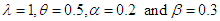

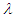 of Laplace Distribution for Different Values of n When
of Laplace Distribution for Different Values of n When 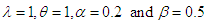

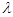 of Laplace Distribution for Different Values of n When
of Laplace Distribution for Different Values of n When 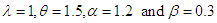

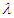 of Laplace Distribution for Different Values of n When
of Laplace Distribution for Different Values of n When 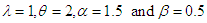

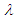 of Laplace distribution for different values of n when
of Laplace distribution for different values of n when 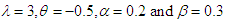

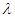 of Laplace Distribution for Different Values of n When
of Laplace Distribution for Different Values of n When 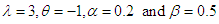

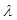 of Laplace Distribution for Different Values of n When
of Laplace Distribution for Different Values of n When 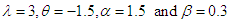

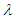 of Laplace Distribution for Different Values of n When
of Laplace Distribution for Different Values of n When