-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2018; 8(5): 140-143
doi:10.5923/j.ajms.20180805.06

A Projection Method for Variational Inequalities over the Fixed Point Set
Hoang Thi Cam Thach1, Nguyen Kieu Linh2
1Department of Mathematics, University of Transport Technology, Vietnam
2Department of Scientific Fundamentals, Posts and Telecommunications Institute of Technology, Hanoi, Vietnam
Correspondence to: Hoang Thi Cam Thach, Department of Mathematics, University of Transport Technology, Vietnam.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, we introduce a new iteration method for solving a variational inequality over the fixed point set of a firmly nonexpansive mapping in 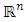 , where the cost function is continuous and monotone, which is called the projection method. The algorithm is a variant of the subgradient method and projection methods.
, where the cost function is continuous and monotone, which is called the projection method. The algorithm is a variant of the subgradient method and projection methods.
Keywords: Variational inequality, Subgradient algorithm, Firmly nonexpansive mapping
Cite this paper: Hoang Thi Cam Thach, Nguyen Kieu Linh, A Projection Method for Variational Inequalities over the Fixed Point Set, American Journal of Mathematics and Statistics, Vol. 8 No. 5, 2018, pp. 140-143. doi: 10.5923/j.ajms.20180805.06.
1. Introduction
- Let
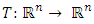 be a firmly nonexpansive mapping, i.e.,
be a firmly nonexpansive mapping, i.e., 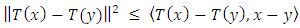 for all
for all 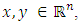 and mapping
and mapping 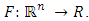 We consider the following variational inequalities over the fixed point set (shortly, VI(F, Fix(T))): Find
We consider the following variational inequalities over the fixed point set (shortly, VI(F, Fix(T))): Find 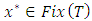 such that
such that 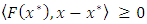
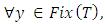 where
where  Problem VI(F,Fix(T)) is a special class of equilibrium problems on the nonempty closed convex constraint set. Many iterative methods for solving such problems have been presented in [1, 2, 3, 4, 5, 8, 9]. In this paper, we investigate a new and efficient global algorithm for solving variational inequalities over the fixed point set of a firmly nonexpansive mapping. To solve the problem, most of current algorithms are based on the metric projection onto a nonempty closed convex constraint set, in general, which is not easy to compute. The fundamental difference here is that, at each main iteration in the proposed algorithm, we only require computing the simple projection. Moreover, by choosing suitable regularization parameters, we show that the iterative sequence globally converges to a solution of Problem VI(F,Fix(T)).The paper is organized as follows. Section 2 recalls some concepts related to variational inequalities over the fixed point set of a nonexpansive mapping, that will be used in the sequel and a new iteration scheme. Section 3 investigates the convergence theorem of the iteration sequences presented in Section 2 as the main results of our paper.
Problem VI(F,Fix(T)) is a special class of equilibrium problems on the nonempty closed convex constraint set. Many iterative methods for solving such problems have been presented in [1, 2, 3, 4, 5, 8, 9]. In this paper, we investigate a new and efficient global algorithm for solving variational inequalities over the fixed point set of a firmly nonexpansive mapping. To solve the problem, most of current algorithms are based on the metric projection onto a nonempty closed convex constraint set, in general, which is not easy to compute. The fundamental difference here is that, at each main iteration in the proposed algorithm, we only require computing the simple projection. Moreover, by choosing suitable regularization parameters, we show that the iterative sequence globally converges to a solution of Problem VI(F,Fix(T)).The paper is organized as follows. Section 2 recalls some concepts related to variational inequalities over the fixed point set of a nonexpansive mapping, that will be used in the sequel and a new iteration scheme. Section 3 investigates the convergence theorem of the iteration sequences presented in Section 2 as the main results of our paper.2. Preliminaries
- We list some well known definitions and the projection under the Euclidean norm, which will be required in our following analysis. Definition 2.1 Let
 be a nonempty closed convex subset of in
be a nonempty closed convex subset of in  we denote the metric projection on
we denote the metric projection on 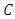 by
by 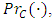 i.e,
i.e, 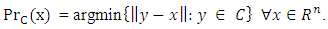 The mapping
The mapping 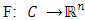 is said to be(i) monotone on
is said to be(i) monotone on 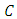 if for each
if for each 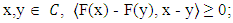 (ii) pseudomonotone on
(ii) pseudomonotone on 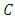 if for each
if for each 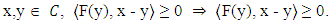 It is well-known that the gradient method in [10] solves the convex optimization problem:
It is well-known that the gradient method in [10] solves the convex optimization problem: 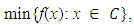 | (2.1) |
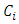 is a closed convex subset of
is a closed convex subset of 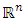 for all i = 1,… ,m,
for all i = 1,… ,m, 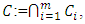 and f is a differentiable convex function on
and f is a differentiable convex function on 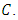 The iteration sequence
The iteration sequence 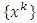 of the method is defined by
of the method is defined by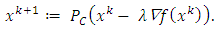 When
When 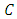 is arbitrary closed convex, in general, computation of the metric projection
is arbitrary closed convex, in general, computation of the metric projection 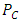 is not necessarily easy and hence it is not effective for solving the convex optimization problem. To overcome this drawback, Yamada in [11] proposed a fixed point iteration method
is not necessarily easy and hence it is not effective for solving the convex optimization problem. To overcome this drawback, Yamada in [11] proposed a fixed point iteration method 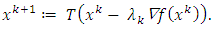 where T is a nonexpansive mapping defined by
where T is a nonexpansive mapping defined by 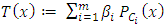 for all
for all 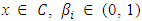 such that
such that 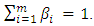 Under certain parameters
Under certain parameters 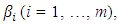 the sequence
the sequence 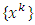 converges a solution to Problem (2.1). Very recently, Iiduka in [6] proposed the fixed point optimization algorithm for solving the following variational inequalities: Finding
converges a solution to Problem (2.1). Very recently, Iiduka in [6] proposed the fixed point optimization algorithm for solving the following variational inequalities: Finding 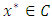 such that
such that 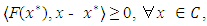 where
where 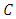 is a nonempty closed convex subset of
is a nonempty closed convex subset of 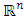 ,
, 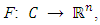 over the fixed point set Fix(T) of a firmly nonexpansive mapping
over the fixed point set Fix(T) of a firmly nonexpansive mapping 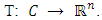 In each iteration of the algorithm, in order to get the next iterate
In each iteration of the algorithm, in order to get the next iterate 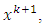 one orthogonal projection onto
one orthogonal projection onto 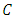 included Fix(T) is calculated, according to the following iterative step. Given the current iterate
included Fix(T) is calculated, according to the following iterative step. Given the current iterate  calculate
calculate 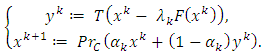 Under certain conditions over parameters
Under certain conditions over parameters 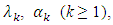 and asymtotic optimization conditions
and asymtotic optimization conditions 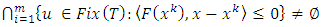 is satisfied. Then, the iterative sequence
is satisfied. Then, the iterative sequence 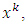 converges a solution to the variational inequalities over the fixed point set of the firmly nonexpansive mapping. In fact, the asymtotic optimization condition, in some cases, is very difficult to define. In order to avoid this requirement, we propose a new iteration method without both the asymtotic optimization condition and computing the metric projection on a closed convex set. Our algorithm is described more detailed as follows. Algorithm 2.2 Initialization. Take a point
converges a solution to the variational inequalities over the fixed point set of the firmly nonexpansive mapping. In fact, the asymtotic optimization condition, in some cases, is very difficult to define. In order to avoid this requirement, we propose a new iteration method without both the asymtotic optimization condition and computing the metric projection on a closed convex set. Our algorithm is described more detailed as follows. Algorithm 2.2 Initialization. Take a point 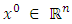 such that
such that 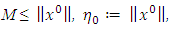 a positive number ρ > 0, and the positive sequences
a positive number ρ > 0, and the positive sequences 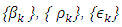 verifying the following conditions:
verifying the following conditions: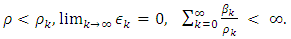 | (2.2) |
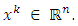 Choose arbitrary
Choose arbitrary 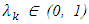 such that
such that 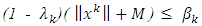 for all
for all 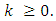 Define
Define 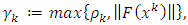
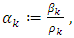 and
and 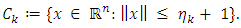
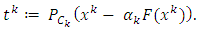 Step 2. Compute
Step 2. Compute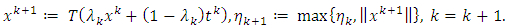 Note that
Note that 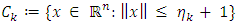 is a closed ball. Therefore, the metric projection
is a closed ball. Therefore, the metric projection 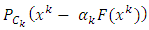 is computed by
is computed by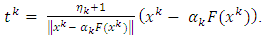
3. Convergent Results
- To investigate the convergence of Algorithm 2.2, we recall the following technical lemmas, which will be used in the sequel.Lemma 3.1 (see [7]) Let
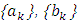 and
and 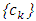 be the three nonnegative sequences satisfying the following condition:
be the three nonnegative sequences satisfying the following condition: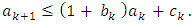 If
If 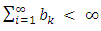 and
and 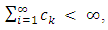 then
then 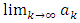 exists.We are now in a position to prove some convergence theorems.Theorem 3.2 Let
exists.We are now in a position to prove some convergence theorems.Theorem 3.2 Let 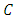 be a nonempty closed convex subset of
be a nonempty closed convex subset of 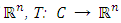 is a firmly nonexpansive mapping such that Fix(T) is bounded by M > 0, and
is a firmly nonexpansive mapping such that Fix(T) is bounded by M > 0, and 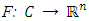 ismonotone. Then, the sequence
ismonotone. Then, the sequence 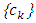 generalized by Algorithm 2.2 converges to a solution of Problem VI(F, Fix(T)).Proof. We divide the proof into five steps.Step 1. For each
generalized by Algorithm 2.2 converges to a solution of Problem VI(F, Fix(T)).Proof. We divide the proof into five steps.Step 1. For each 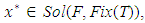 we have
we have | (3.1) |
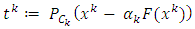 it follows that
it follows that 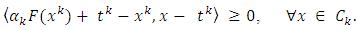 | (3.2) |
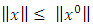 for all
for all 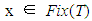 and
and 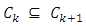 for all k ≥ 0, we have
for all k ≥ 0, we have 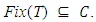 Then, substituting
Then, substituting 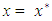 into (3.2), we get
into (3.2), we get 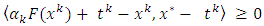 Combinating this and the inequality
Combinating this and the inequality
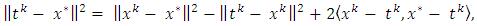 we have
we have 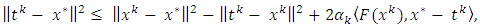 Since (3.3),
Since (3.3), 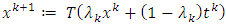 and the equaltity
and the equaltity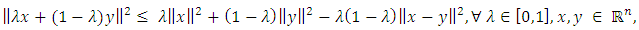 | (3.4) |
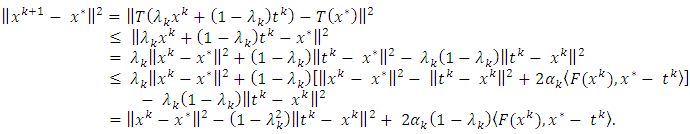 Thus
Thus 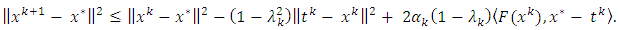 | (3.5) |
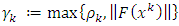 and
and 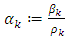 it follows that
it follows that 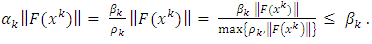 | (3.6) |
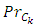 and (3.6), we have
and (3.6), we have
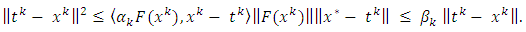 | (3.7) |
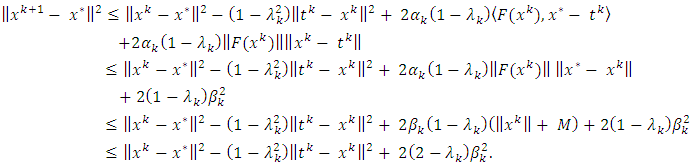 This implies (3.1). Step 2. Claim that
This implies (3.1). Step 2. Claim that 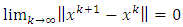 and
and 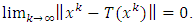 Indeed, using (3.3), (3.4) and the definition of the firmly nonexpansive mapping, we have
Indeed, using (3.3), (3.4) and the definition of the firmly nonexpansive mapping, we have 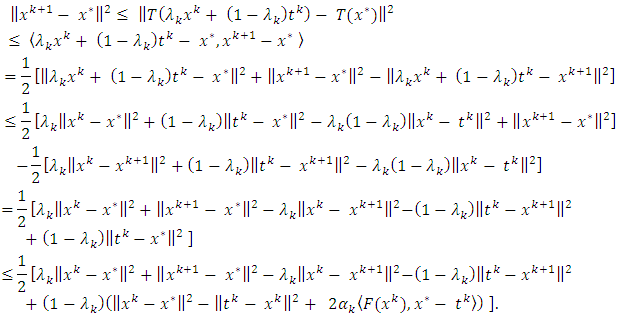 Hence, we have
Hence, we have 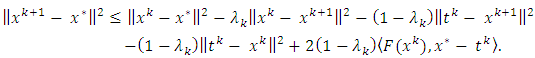 | (3.8) |
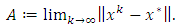 | (3.9) |
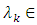
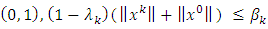 and
and 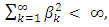 it follows that
it follows that 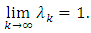 Combinating this, (3.8) and (3.9), we get
Combinating this, (3.8) and (3.9), we get 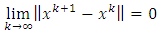 Using this, the nonexpansive property of T and
Using this, the nonexpansive property of T and 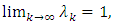 have
have 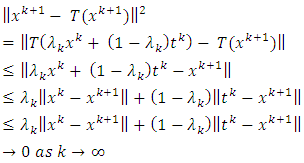 Since
Since 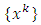 is bounded, there exists
is bounded, there exists 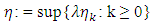
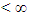 and a subsequence
and a subsequence 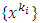 which converges to
which converges to 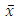 as i → ∞. Step 3. Claim that
as i → ∞. Step 3. Claim that 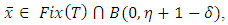 where
where 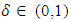 and the open ball is defined by
and the open ball is defined by 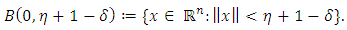 Indeed, from
Indeed, from 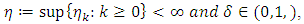 it follows that the existence of
it follows that the existence of 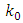 such that for
such that for 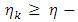
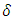 for all
for all 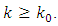 It means that
It means that 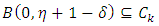 for all
for all 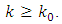 Then, we have
Then, we have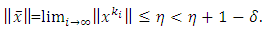 Thus,
Thus, 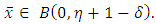 Now we suppose that
Now we suppose that 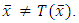 By Step 2 and Opial’s condition, we get
By Step 2 and Opial’s condition, we get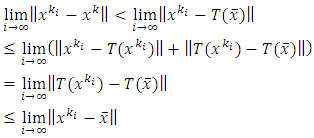 This is a contradiction. So,
This is a contradiction. So, 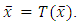 Step 4. Claim that
Step 4. Claim that 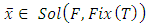 and the sequence
and the sequence 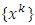 converges to
converges to 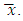 Indeed, from (3.6), it follows that
Indeed, from (3.6), it follows that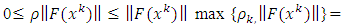
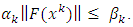 Using
Using 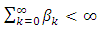 and
and 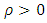 , we have
, we have 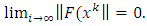 Combinating this and Step 3, we have
Combinating this and Step 3, we have 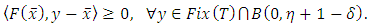 Denote
Denote 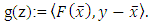 Then, g is convex and
Then, g is convex and 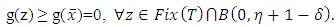 Thus,
Thus, 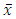 is a local minimizer of g. Since Fix(T) is nonempty convex,
is a local minimizer of g. Since Fix(T) is nonempty convex, 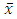 is also a global minimizer of g, i.e.,
is also a global minimizer of g, i.e., 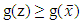 for all
for all 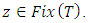 This means that
This means that 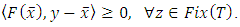 So,
So, 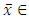 Sol(F, Fix(T)). To prove
Sol(F, Fix(T)). To prove 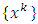 converges to
converges to 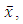 we suppose that the subsequence
we suppose that the subsequence 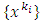 also converges to
also converges to 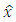 as j → ∞. By a same way, we also have
as j → ∞. By a same way, we also have 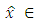 VI(F, Fix(T)). Suppose that
VI(F, Fix(T)). Suppose that 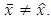 Then, using Opial’s condition, we have
Then, using Opial’s condition, we have 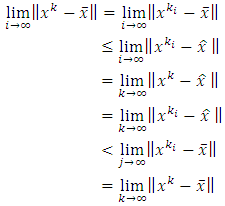 This is a contradiction. Thus, the sequence
This is a contradiction. Thus, the sequence 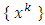 converges to
converges to 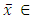 Sol(F, Fix(T)).
Sol(F, Fix(T)).4. Conclusions
- This paper presented an iterative algorithm for solving variational inequalities over the fixed point set of a nonexpansive mapping T. By choosing the suitable regular parameters, we show that the sequences generated by the algorithm globally converge to a solution of Problem VI(F, fix(T)). Comparing with the current methods, the fundamental difference here is that, the algorithm only requires the continuity of the mapping F and convergence of the proposed algorithms only require F to satisfy monotonicity. Moreover, in general, computing the exact subgradient of a subdifferentiable function is too expensive, our algorithm only requires to compute approximate.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML