-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2018; 8(5): 126-135
doi:10.5923/j.ajms.20180805.04

A Size-Biased Poisson-Aradhana Distribution with Applications
Rama Shanker1, Kamlesh Kumar Shukla1, Ravi Shanker2, Tekie Asehun Leonida3
1Department of Statistics, College of Science, Eritrea Institute of Technology, Asmara, Eritrea
2Department of Mathematics, G.L.A. College, N.P University, Daltonganj, Jharkhand, India
3Department of Applied Mathematics, University of Twente, The Netherlands
Correspondence to: Rama Shanker, Department of Statistics, College of Science, Eritrea Institute of Technology, Asmara, Eritrea.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this present paper, a size-biased Poisson-Aradhana distribution (SBPAD) has been proposed and its nature has been studied graphically. Its moments and moments based measures including coefficients of variation, skewness, kurtosis and index of dispersion have been obtained and their natures have been discussed graphically. The unimodality and increasing hazard rate function of the distribution has been discussed. Method of moments and the method of maximum likelihood have been discussed for estimating the parameter. Applications of SBPAD have been explained through three examples and it gives much better fit over size-biased Poisson distribution (SBPD) and size-biased Poisson-Lindley distribution (SBPLD).
Keywords: Size-biasing, Aradhana distribution, Poisson-Aradhana distribution, Moments, Skewness, Kurtosis, Estimation, Applications
Cite this paper: Rama Shanker, Kamlesh Kumar Shukla, Ravi Shanker, Tekie Asehun Leonida, A Size-Biased Poisson-Aradhana Distribution with Applications, American Journal of Mathematics and Statistics, Vol. 8 No. 5, 2018, pp. 126-135. doi: 10.5923/j.ajms.20180805.04.
Article Outline
1. Introduction
- Let a random variable
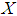 has probability distribution
has probability distribution 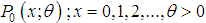 . Suppose the sample units are selected or weighted from the distribution with probability proportional to
. Suppose the sample units are selected or weighted from the distribution with probability proportional to 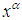 . Then the corresponding size-biased distribution of order
. Then the corresponding size-biased distribution of order 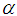 can be defined by its probability mass function (pmf)
can be defined by its probability mass function (pmf)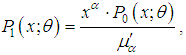 | (1.1) |
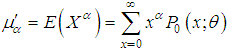 . The simple size-biased distribution and area-biased distribution are the particular cases of (1.1) for
. The simple size-biased distribution and area-biased distribution are the particular cases of (1.1) for 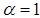 and
and  respectively. Note that simple size-biased distribution has applications in size-biased sampling and area-biased distribution has been used in area-biased sampling.When organism occurs in groups and the size of the group influences the probability of detection, size-biased distributions are the appropriate choice. Size-biased distributions are a special class of weighted distributions which arise naturally in many real life situations when observations from a sample are recorded with probability proportional to some measure of unit size, known as probability proportional to size (PPS). In the field applications, size-biased distributions can arise due to sampling of individuals with unequal probability by design and unequal detection probability. The concept of weighted distributions can be traced to the study of the effect of methods of ascertainment upon frequencies by Fisher (1934). In extending the basic ideas of Fisher, Rao (1965) have seen the need for a unifying concept and identified various sampling situations that can be modeled by weighted distributions. Size-biased distributions have applications in almost every branch of knowledge namely, social science, econometrics, environmental science, biomedical science, human demography, ecology, geology, forestry, are some among others. The fitting of distributions of diameter at breast height (DBH) data arising from horizontal point sampling (HPS) using size-biased distributions has been discussed by Van Duesen (1986). Similarly, the analysis of HPS diameter increment data using size-biased distributions has been discussed by Lappi and Bailey (1987). Patil and Rao (1977, 1978) have detailed discussions and applications of size-biased distributions to the analysis and modeling of observed data relating to human population and ecology. Patil (1991, 1996, and 1997) has pursued weighted distributions for the purpose of encountered data analysis, equilibrium population analysis subject to harvesting and predation, meta-analysis incorporating publication bias and heterogeneity, modeling cluster and extraneous variation, etc., and has detailed discussion on applications of size-biased distributions in biostatistics, ecology, environment and risk assessment. A number of papers have appeared during a short period of time implicitly using the concept of weighted and size-biased distributions and their applications in various fields of knowledge by researchers in statistics, namely, Scheaffer (1972), Patil and Ord (1976), Singh and Maddala (1976), Patil (1981), McDonald (1984), Drummer and McDonald (1987), Gove (2000, 2003), Correa and Wolfson (2007), Ducey (2009), Alavi and Chinipardaz (2009), Ducey and Gove (2015), are some among others.Shanker (2017) has introduced Poisson-Aradhana distribution (PAD) defined by pmf
respectively. Note that simple size-biased distribution has applications in size-biased sampling and area-biased distribution has been used in area-biased sampling.When organism occurs in groups and the size of the group influences the probability of detection, size-biased distributions are the appropriate choice. Size-biased distributions are a special class of weighted distributions which arise naturally in many real life situations when observations from a sample are recorded with probability proportional to some measure of unit size, known as probability proportional to size (PPS). In the field applications, size-biased distributions can arise due to sampling of individuals with unequal probability by design and unequal detection probability. The concept of weighted distributions can be traced to the study of the effect of methods of ascertainment upon frequencies by Fisher (1934). In extending the basic ideas of Fisher, Rao (1965) have seen the need for a unifying concept and identified various sampling situations that can be modeled by weighted distributions. Size-biased distributions have applications in almost every branch of knowledge namely, social science, econometrics, environmental science, biomedical science, human demography, ecology, geology, forestry, are some among others. The fitting of distributions of diameter at breast height (DBH) data arising from horizontal point sampling (HPS) using size-biased distributions has been discussed by Van Duesen (1986). Similarly, the analysis of HPS diameter increment data using size-biased distributions has been discussed by Lappi and Bailey (1987). Patil and Rao (1977, 1978) have detailed discussions and applications of size-biased distributions to the analysis and modeling of observed data relating to human population and ecology. Patil (1991, 1996, and 1997) has pursued weighted distributions for the purpose of encountered data analysis, equilibrium population analysis subject to harvesting and predation, meta-analysis incorporating publication bias and heterogeneity, modeling cluster and extraneous variation, etc., and has detailed discussion on applications of size-biased distributions in biostatistics, ecology, environment and risk assessment. A number of papers have appeared during a short period of time implicitly using the concept of weighted and size-biased distributions and their applications in various fields of knowledge by researchers in statistics, namely, Scheaffer (1972), Patil and Ord (1976), Singh and Maddala (1976), Patil (1981), McDonald (1984), Drummer and McDonald (1987), Gove (2000, 2003), Correa and Wolfson (2007), Ducey (2009), Alavi and Chinipardaz (2009), Ducey and Gove (2015), are some among others.Shanker (2017) has introduced Poisson-Aradhana distribution (PAD) defined by pmf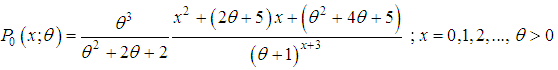 | (1.2) |
 of the Poisson distribution follows Aradhana distribution introduced by Shanker (2016) having probability density function (pdf.)
of the Poisson distribution follows Aradhana distribution introduced by Shanker (2016) having probability density function (pdf.)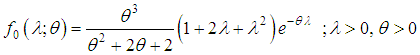 | (1.3) |
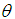 can be obtained as
can be obtained as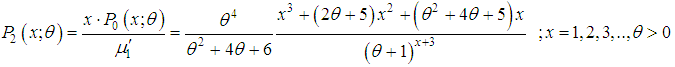 | (1.4) |
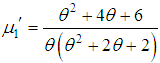 is the population mean of the PAD having pmf. (1.2). The pmf of SBPAD (1.4) can also be obtained from the size-biased Poisson distribution (SPBD) having pmf
is the population mean of the PAD having pmf. (1.2). The pmf of SBPAD (1.4) can also be obtained from the size-biased Poisson distribution (SPBD) having pmf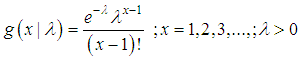 | (1.5) |
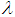 of SBPD follows the size-biased Aradhana distribution (SBAD) having pdf
of SBPD follows the size-biased Aradhana distribution (SBAD) having pdf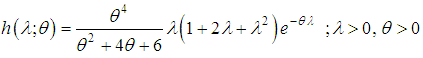 | (1.6) |
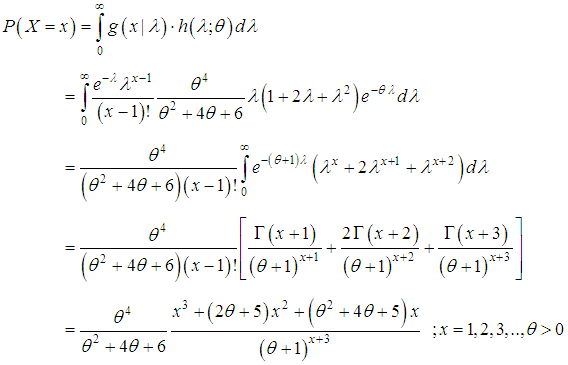 | (1.7) |
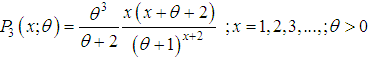 | (1.8) |
 has been shown in figure 1.
has been shown in figure 1.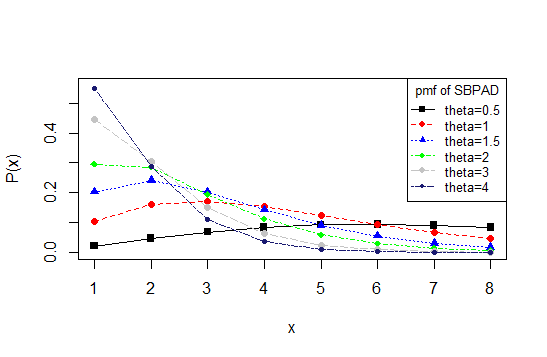 | Figure 1. Nature of SBPAD for some values of the parameter θ |
2. Moments, Skewness, Kurtosis and Index of Dispersion
- The rth factorial moment about origin, using (1.7), of the SBPAD (1.4) can be obtained as
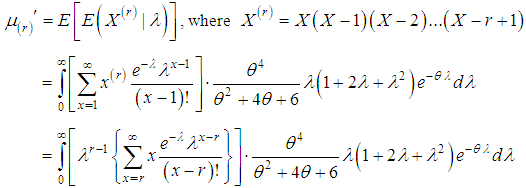 Taking
Taking 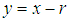 , we get
, we get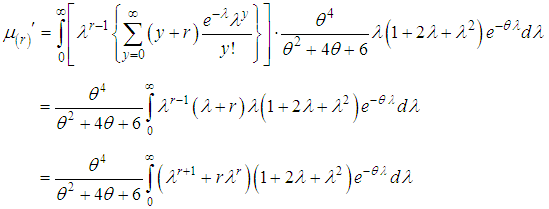 After a simple algebraic simplification using gamma integral, the rth factorial moment about origin of SBPAD (1.4) can be expressed as
After a simple algebraic simplification using gamma integral, the rth factorial moment about origin of SBPAD (1.4) can be expressed as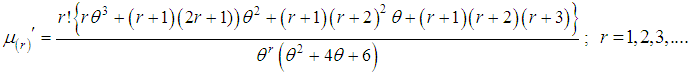 | (2.1) |
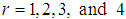 in (2.1) the first four factorial moments can be obtained. Then using the relationship between moments about origin (raw moments) and factorial moments, the first four moments about origin of the SBPAD (1.4) are thus obtained as
in (2.1) the first four factorial moments can be obtained. Then using the relationship between moments about origin (raw moments) and factorial moments, the first four moments about origin of the SBPAD (1.4) are thus obtained as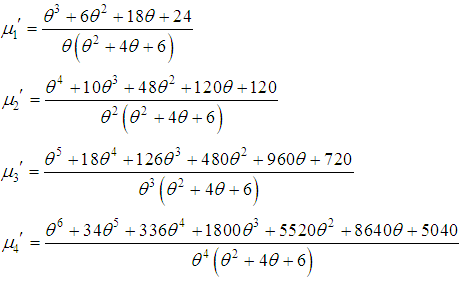 Now, using the relationship
Now, using the relationship 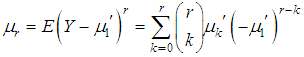 between central moments and raw moments, the central moments of the SBPAD (1.4) are given by
between central moments and raw moments, the central moments of the SBPAD (1.4) are given by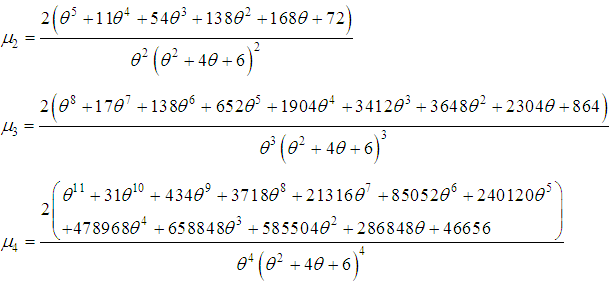 The expressions for coefficient of variation
The expressions for coefficient of variation 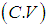 , coefficient of Skewness
, coefficient of Skewness 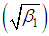 , coefficient of Kurtosis
, coefficient of Kurtosis 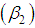 and index of dispersion
and index of dispersion 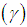 of the SBPAD (1.4) are thus obtained as
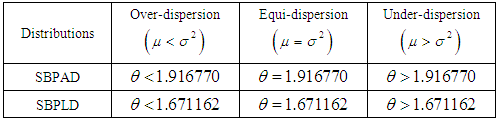
of the SBPAD (1.4) are thus obtained as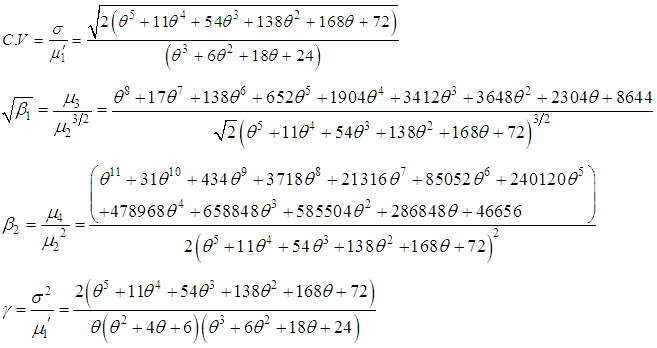 The dispersion (over-dispersion, equi-dispersion and under-dispersion) of SBPAD and SBPLD for parameter
The dispersion (over-dispersion, equi-dispersion and under-dispersion) of SBPAD and SBPLD for parameter  are presented in table 1.
are presented in table 1.
|
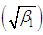 , coefficient of Kurtosis
, coefficient of Kurtosis 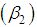 and index of dispersion
and index of dispersion 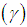 of SBPAD for varying values of parameter
of SBPAD for varying values of parameter 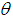 are shown graphically in figure 2
are shown graphically in figure 2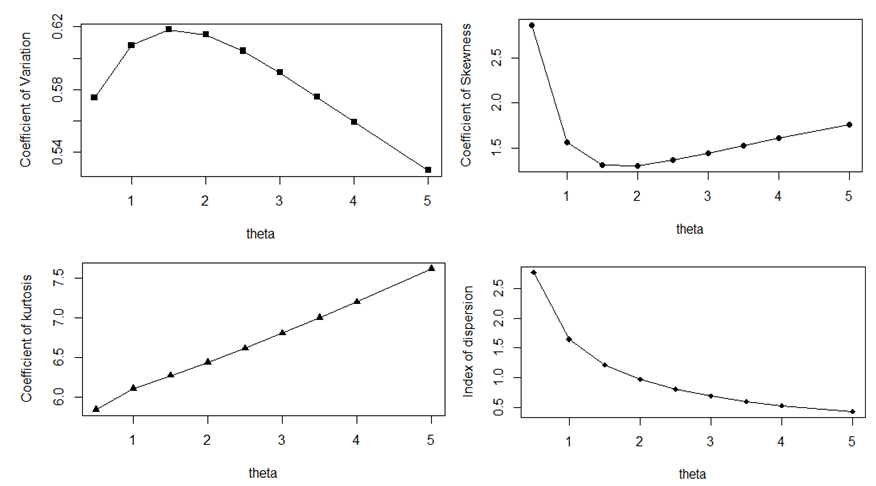 | Figure 2. Nature of coefficient of variation, coefficient of Skewness, coefficient of Kurtosis, and index of dispersion of SBPAD for varying values of parameter θ |
3. Statistical Properties
3.1. Unimodality and Increasing Failure Rate
- Since
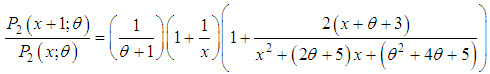 is a deceasing function of x,
is a deceasing function of x, 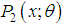 is log-concave and this means that SBPAD is unimodal, has an increasing failure rate (IFR), and hence increasing failure rate average (IFRA). Also, it is new better than used in expectation (NBUE) and has decreasing mean residual life (DMRL). A discussion about definitions, concepts and interrelationship between these reliability concepts are available in Barlow and Proschan (1981).
is log-concave and this means that SBPAD is unimodal, has an increasing failure rate (IFR), and hence increasing failure rate average (IFRA). Also, it is new better than used in expectation (NBUE) and has decreasing mean residual life (DMRL). A discussion about definitions, concepts and interrelationship between these reliability concepts are available in Barlow and Proschan (1981).3.2. Generating Function
- The probability generating function of the SBPAD (1.4) can be obtained as
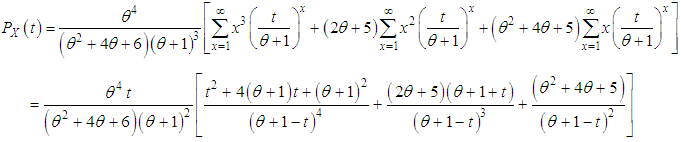 Thus, the moment generating function of the SBPAD (1.4) is given by
Thus, the moment generating function of the SBPAD (1.4) is given by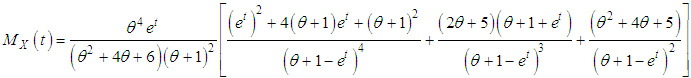
4. Estimation
4.1. Estimation by Method of Moments
- Since SBPAD has only one parameter to be estimated, equating the population mean to the corresponding sample mean, method of moments estimate (MOME)
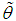 of the parameter
of the parameter 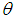 of SBPAD is the solution of the following cubic equation in
of SBPAD is the solution of the following cubic equation in 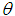
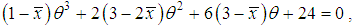 where
where 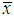 is the sample mean. This equation can be easily solved using Newton-Raphson method for MOME estimate
is the sample mean. This equation can be easily solved using Newton-Raphson method for MOME estimate 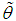 of
of 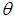 of SBPAD.
of SBPAD.4.2. Estimation by Maximum Likelihood Method
- Let
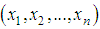 be a random sample of size n from the SBPAD (1.4). Suppose
be a random sample of size n from the SBPAD (1.4). Suppose 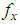 be the observed frequency in the sample corresponding to
be the observed frequency in the sample corresponding to 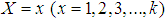 such that
such that 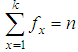 , k being the largest observed value having non-zero frequency. Then, the log likelihood function,
, k being the largest observed value having non-zero frequency. Then, the log likelihood function, 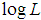 , of the SBPAD (1.4) can be expressed as
, of the SBPAD (1.4) can be expressed as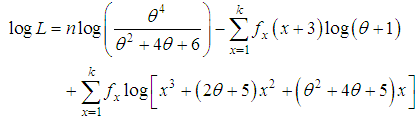 The first derivative of the log likelihood function can be given by
The first derivative of the log likelihood function can be given by 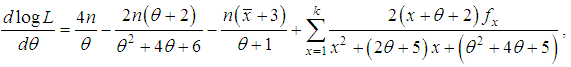 where
where 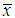 is the sample mean.The maximum likelihood estimate (MLE)
is the sample mean.The maximum likelihood estimate (MLE) 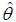 of the parameter
of the parameter 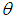 of SBPAD (1.4) is thus the solution of the following log likelihood equation
of SBPAD (1.4) is thus the solution of the following log likelihood equation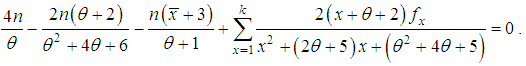 This non-linear log likelihood equation can be solved by any iterative methods. Here we used Newton-Raphson method to solve above equation. Note that the initial value for Newton-Raphson method is the value given by MOME of the parameter θ.
This non-linear log likelihood equation can be solved by any iterative methods. Here we used Newton-Raphson method to solve above equation. Note that the initial value for Newton-Raphson method is the value given by MOME of the parameter θ.5. Goodness of Fit
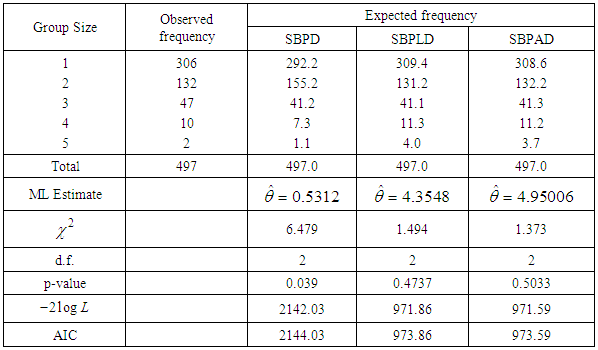
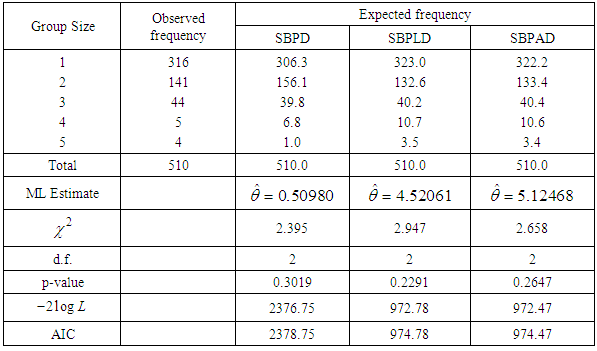
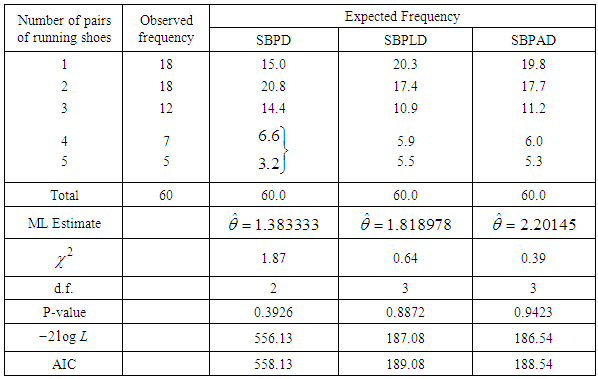
- We know that when organism occurs in groups and the group size influences the probability of detection, size-biased distributions are the appropriate choice to model the datasets. In this section, three examples of real datasets, two from the size distribution of freely-forming small group at various public places, available in James (1953) and Coleman and James (1961) and one from the number of pairs of running shoes owned by 60 members of an athletic club, available in Simonoff (2003, p. 100), have been taken for testing the goodness of fit of SBPAD and compared with SBPD and SBPLD. The estimation of parameter of all distributions is based on MLE. The criterion for the selection of best distribution is based on the values of chi-square
 ,
, 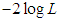 and AIC (Akaike Information Criteria). The AIC is calculated using
and AIC (Akaike Information Criteria). The AIC is calculated using 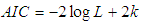 , where k the number of parameters involved in the distribution. The best distribution is the distribution whose values of chi-square,
, where k the number of parameters involved in the distribution. The best distribution is the distribution whose values of chi-square, 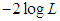 and AIC is the lowest. Clearly SBPAD gives a much better fit as compared with SBPD and SBPLD, and, therefore, it should be considered an important distribution over SBPD and SBPLD.
and AIC is the lowest. Clearly SBPAD gives a much better fit as compared with SBPD and SBPLD, and, therefore, it should be considered an important distribution over SBPD and SBPLD.
|
|
|
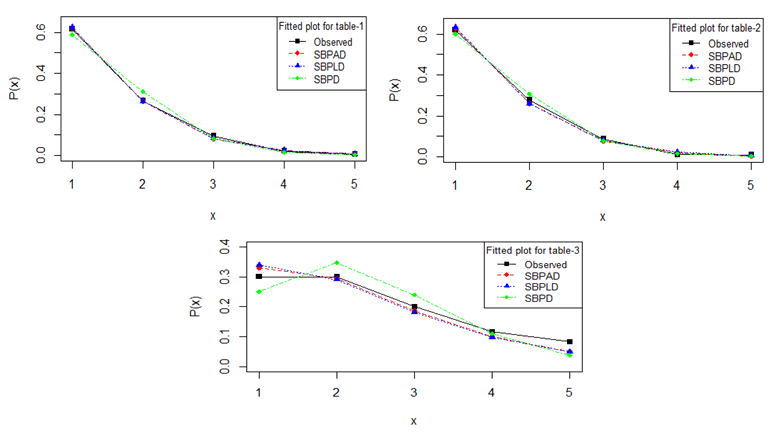 | Figure 3. Fitted probability plots for distributions for considered datasets |
6. Concluding Remarks
- In this paper, a size-biased Poisson –Aradhana distribution (SBPAD) has been proposed by size-biasing the discrete Poisson- Aradhana distribution (PAD) suggested by Shanker (2017), a Poisson mixture of Aradhana distribution introduced by Shanker (2016). Its statistical constants including coefficients of variation, skewness, kurtosis, and index of dispersion have been studied. Both the method of moments and the maximum likelihood estimation has been discussed Applications of SBPAD have been explained with three examples of real datasets and the goodness of fit shows that SBPAD gives better fit over SBPD and SBPLD.
ACKNOWLEDGEMENTS
- Authors are grateful to the editor in chief of the journal and the anonymous reviewer for fruitful comments which improved the quality of the paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML