-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2018; 8(2): 50-55
doi:10.5923/j.ajms.20180802.03

Nαc – Open Sets and Their Basic Properties in Topological Spaces
Nadia M. Ali Abbas1, Shuker Mahmood Khalil2
1Ministry of Education, Baghdad, Iraq
2Department of Mathematics, College of Science, Basra University, Basra, Iraq
Correspondence to: Shuker Mahmood Khalil, Department of Mathematics, College of Science, Basra University, Basra, Iraq.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this work, we first introduce the concept of 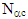 -open sets and we study some of their basic properties. Furthermore, some relationships between our concepts with some classes of sets are investigated. Moreover, several examples are given to illustrate the concepts introduced in this paper.
-open sets and we study some of their basic properties. Furthermore, some relationships between our concepts with some classes of sets are investigated. Moreover, several examples are given to illustrate the concepts introduced in this paper.
Keywords:
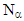 -Open sets,
-Open sets, 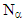 - continuity mappings
- continuity mappings
Cite this paper: Nadia M. Ali Abbas, Shuker Mahmood Khalil, Nαc – Open Sets and Their Basic Properties in Topological Spaces, American Journal of Mathematics and Statistics, Vol. 8 No. 2, 2018, pp. 50-55. doi: 10.5923/j.ajms.20180802.03.
Article Outline
1. Introduction
- The sets play a very important role in General Topology. There are many types of these sets like β-open sets, regularopen sets, semi regularopen sets, b-open sets and others were discussed in soft setting and fuzzy setting see ([4], [5], [14], [15]). Also, some of these sets were applied to investigate new spaces, new maps and new separation axioms see ([9]-[13]). In 1968, Velicko [18], investigated the definitions of δ -open and θ -open, where A is said to be δ -open (resp., θ -open) if for any
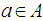 , there exists an open set B satisfies
, there exists an open set B satisfies 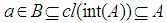 (resp.,
(resp., 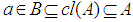 ). Di Maio and Noiri [8] showed that
). Di Maio and Noiri [8] showed that 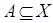 in a space X is said to be semi-θ -open if for each
in a space X is said to be semi-θ -open if for each 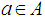 , there exists a semi-open set B satisfies
, there exists a semi-open set B satisfies 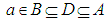 , where D is a semi closure of B. The family of all
, where D is a semi closure of B. The family of all 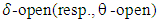 is denoted by
is denoted by  An α-open sets are one of these sets. It was first studied in 1965 by O. Njasted. These sets form a topology on X which is finer than τ, see [17], [3]. The notion of Nα -open set was first studied in 2015 using the concept of an α – open set, it was studied by N. A. Dawood and N. M. Ali, see [6]. Here in this paper an attempt has been made to employ the notion of Nα -open set to show a new kind of sets that called
An α-open sets are one of these sets. It was first studied in 1965 by O. Njasted. These sets form a topology on X which is finer than τ, see [17], [3]. The notion of Nα -open set was first studied in 2015 using the concept of an α – open set, it was studied by N. A. Dawood and N. M. Ali, see [6]. Here in this paper an attempt has been made to employ the notion of Nα -open set to show a new kind of sets that called 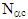 -Open set and investigate it's properties. In this paper (X,τ) or a space X always denote a topological space on which no separation axioms are assumed unless explicitly stated. Assume
-Open set and investigate it's properties. In this paper (X,τ) or a space X always denote a topological space on which no separation axioms are assumed unless explicitly stated. Assume 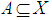 in a space X, cl(A) and int(A) refer to the closure and interior of A respectively.
in a space X, cl(A) and int(A) refer to the closure and interior of A respectively.2. Preliminary Definitions
- Definition (2.1) [17], [16], [18]Let A be a set in space X. We say A is an α-open (resp., preopen and regularopen) if A
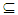 (int(cl(int(A))),(resp., A
(int(cl(int(A))),(resp., A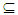 int(cl(A))and A=int(cl(A)). Also, their complements are an α- closed (resp., preclosed and regularclosed)). The family of all α- open,(resp. preopen and regularopen) is denoted by αO(X),(resp., PO(X) and RO(X)). Definition (2.2) [6] Let A be a set in a space X. We say A is an Nα-open if there exists non-empty an α-open set B such that cl(B)
int(cl(A))and A=int(cl(A)). Also, their complements are an α- closed (resp., preclosed and regularclosed)). The family of all α- open,(resp. preopen and regularopen) is denoted by αO(X),(resp., PO(X) and RO(X)). Definition (2.2) [6] Let A be a set in a space X. We say A is an Nα-open if there exists non-empty an α-open set B such that cl(B)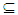 A, and it's complement is called an Nα -closed. Also, the family of all Nα- open (resp., Nα-closed) sets are denoted by NαO(X), (resp., NαC(X)). Remark (2.3) [6] (i) X and ϕ are Nα – open sets in every topological space. (ii) Every subset in discrete space is Nα –open set. (iii) In the usual topological space every interval is Nα- Open set. (iv) Every closed and open (resp., α-open, preopen and
A, and it's complement is called an Nα -closed. Also, the family of all Nα- open (resp., Nα-closed) sets are denoted by NαO(X), (resp., NαC(X)). Remark (2.3) [6] (i) X and ϕ are Nα – open sets in every topological space. (ii) Every subset in discrete space is Nα –open set. (iii) In the usual topological space every interval is Nα- Open set. (iv) Every closed and open (resp., α-open, preopen and 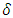 -open) is Nα-open set. (v) If A is Nα-open set. Then
-open) is Nα-open set. (v) If A is Nα-open set. Then 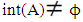 . Proposition (2.4) [6] If A is a closed set of a space X. Then A is Nα – open set if and only if
. Proposition (2.4) [6] If A is a closed set of a space X. Then A is Nα – open set if and only if 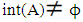 . Proposition (2.5) [6] Finite union of Nα- open sets is Nα- open. Theorem (2.6) [1] The following statements are equivalent: (i) X is Alexindroff space. (ii) For any an open (resp.,closed) sets then their intersection(resp., union) is an open(resp., closed) also. Definition (2.7) [7] Let X be a space. If every an open set of X is a closed. Then X is called Locally Indiscrete space. Proposition (2.8) [2] For any set A of a space X. Then A is clopen if and only if preopen and closed. Proposition (2.9) [6] Let Y be a subspace of a space X such that A
. Proposition (2.5) [6] Finite union of Nα- open sets is Nα- open. Theorem (2.6) [1] The following statements are equivalent: (i) X is Alexindroff space. (ii) For any an open (resp.,closed) sets then their intersection(resp., union) is an open(resp., closed) also. Definition (2.7) [7] Let X be a space. If every an open set of X is a closed. Then X is called Locally Indiscrete space. Proposition (2.8) [2] For any set A of a space X. Then A is clopen if and only if preopen and closed. Proposition (2.9) [6] Let Y be a subspace of a space X such that A 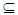 Y
Y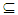 X. Then:(i) If A∈ NαO (X)(resp.NαC (X)), then A∈ NαO(Y)(resp. NαC(Y)).(ii) If A∈ NαO(Y)(resp., NαC (Y)), then A∈ NαO(X)(resp. NαC(X)) where Y is clopen set in X. Theorem (2. 10) [6] A space X is Nα** - regular, if and only if all Nα-open set A containing x there exists an open set G containing x such that x∈G
X. Then:(i) If A∈ NαO (X)(resp.NαC (X)), then A∈ NαO(Y)(resp. NαC(Y)).(ii) If A∈ NαO(Y)(resp., NαC (Y)), then A∈ NαO(X)(resp. NαC(X)) where Y is clopen set in X. Theorem (2. 10) [6] A space X is Nα** - regular, if and only if all Nα-open set A containing x there exists an open set G containing x such that x∈G 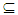 cl(G)
cl(G)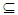 A. Theorem (2.11) [6](i) If a space X is Nα** - regular. Then every Nα-open set is an open set. (ii) If a space X is Nα** - regular and Alexindroof. Then A is Nα-open if and only if is clopen.
A. Theorem (2.11) [6](i) If a space X is Nα** - regular. Then every Nα-open set is an open set. (ii) If a space X is Nα** - regular and Alexindroof. Then A is Nα-open if and only if is clopen.3. Nαc - Open Set and Their Basic Properties
- A new kind of sets called Nαc-open using the concept of Nα- open set is studied in this section. Some definitions, propositions and counterexamples are given. Definition (3.1) An Nα-open set A of a space X is Nαc- open if for all x∈ A there exists closed set F such that x∈ F
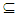 A, it's complement is called Nαc- closed set. The family of all Nαc-open (resp.Nαc- closed) is denoted by NαcO(X)(resp.,(NαcC(X)). Proposition (3.2)A∈ NαcO(X) if and only if A∈NαO(X) as well as a union of closed sets. Proof: Obvious The above definition refer to every Nαc- open is Nα- open set, but the converse need not be true in general. See the following example: Example (3.3)Consider X ={a,b,c,d,e,} and τ = {X,{a},{b,c}, {a,b,c},ϕ}. Let A={a,b,d,e}∈ NαO(X) but A ∉ NαcO(X) since only {b,c,d,e} is closed set and contains b. However, {b,c,d,e} is not contained in A. Corollary (3.4) (i) Every closed Nα-open set is Nαc –open set. Proof: Follows from Proposition (3.2). (ii) Every closed and α-open (resp.
A, it's complement is called Nαc- closed set. The family of all Nαc-open (resp.Nαc- closed) is denoted by NαcO(X)(resp.,(NαcC(X)). Proposition (3.2)A∈ NαcO(X) if and only if A∈NαO(X) as well as a union of closed sets. Proof: Obvious The above definition refer to every Nαc- open is Nα- open set, but the converse need not be true in general. See the following example: Example (3.3)Consider X ={a,b,c,d,e,} and τ = {X,{a},{b,c}, {a,b,c},ϕ}. Let A={a,b,d,e}∈ NαO(X) but A ∉ NαcO(X) since only {b,c,d,e} is closed set and contains b. However, {b,c,d,e} is not contained in A. Corollary (3.4) (i) Every closed Nα-open set is Nαc –open set. Proof: Follows from Proposition (3.2). (ii) Every closed and α-open (resp. 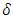 -open) set is Nαc-open set. Proof: Follows from Remark (2.3) (iv)) and Corollary (3.4(i)). (iii) X and ϕ are Nαc –open sets in every topological space. Proof: Follows from Remark (2.3) and Corollary (3.4(i)). Proposition (3.5) If A∈ NαcO(X) then,
-open) set is Nαc-open set. Proof: Follows from Remark (2.3) (iv)) and Corollary (3.4(i)). (iii) X and ϕ are Nαc –open sets in every topological space. Proof: Follows from Remark (2.3) and Corollary (3.4(i)). Proposition (3.5) If A∈ NαcO(X) then, 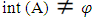 . Proof: If A∈ NαcO(X) then A∈NαO(X) this implies
. Proof: If A∈ NαcO(X) then A∈NαO(X) this implies 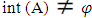 see Remark (2.3). The following example explains that the converse of Proposition of (3. 5) is not true. Example (3.6)Consider X = {a, b, c} with
see Remark (2.3). The following example explains that the converse of Proposition of (3. 5) is not true. Example (3.6)Consider X = {a, b, c} with 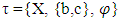 . Let A={b,c} then,
. Let A={b,c} then, 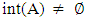 but A∉NαcO(X) because A∉NαO (X).Proposition (3.7) If A is a closed set of a space X. Then A∈ NαcO(X) if and only if
but A∉NαcO(X) because A∉NαO (X).Proposition (3.7) If A is a closed set of a space X. Then A∈ NαcO(X) if and only if 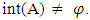 Proof: The first part follows from Proposition (3.5). The other part assume that
Proof: The first part follows from Proposition (3.5). The other part assume that 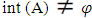 , implies that A is Nα- open set see Proposition(2.4). Therefore, A∈ NαcO(X) see Corollary(3.4).Proposition (3.8)If A∈ NαcO(X), then cl(A)∈ NαcO(X). Proof: Suppose that A∈ NαcO(X) then, by Proposition (3.5)
, implies that A is Nα- open set see Proposition(2.4). Therefore, A∈ NαcO(X) see Corollary(3.4).Proposition (3.8)If A∈ NαcO(X), then cl(A)∈ NαcO(X). Proof: Suppose that A∈ NαcO(X) then, by Proposition (3.5) 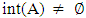 where int(A) is an open set so it is an α –open and it's closure contain in cl(A) this implies cl(A)∈NαO(X) thus by Corollary.(3.4) cl(A)∈NαcO(X). Proposition (3.9)Finite union of Nαc- open sets is Nαc – open. Proof: Let Ai be Nαc-open set, i=1, 2,…n. Thus Ai is Nα-open set, hence by Proposition (2.5)
where int(A) is an open set so it is an α –open and it's closure contain in cl(A) this implies cl(A)∈NαO(X) thus by Corollary.(3.4) cl(A)∈NαcO(X). Proposition (3.9)Finite union of Nαc- open sets is Nαc – open. Proof: Let Ai be Nαc-open set, i=1, 2,…n. Thus Ai is Nα-open set, hence by Proposition (2.5)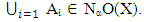 Let
Let 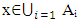 then there exists
then there exists 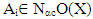 such that x∈Ai for some i= 1,2, …n, thus there exists closed set F such that x∈ F
such that x∈Ai for some i= 1,2, …n, thus there exists closed set F such that x∈ F 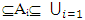 Ai, hence
Ai, hence 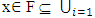 Ai. Thus
Ai. Thus 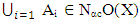 .Definition (3.10)Let A
.Definition (3.10)Let A 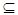 X. The union of all Nαc - open sets contain in A is called Nαc -interior of A briefly Nαc-int(A). Proposition (3.11) Let A be a set of a space X. Then:(i) Nαc int(A)
X. The union of all Nαc - open sets contain in A is called Nαc -interior of A briefly Nαc-int(A). Proposition (3.11) Let A be a set of a space X. Then:(i) Nαc int(A) 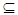 A.(ii) If A
A.(ii) If A 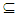 B then, Nαc int(A)
B then, Nαc int(A) 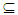 Nαc int(B).(iii) If A is Nαc – open set then, A = Nαc int(A). Proof: Obvious. Corollary (3.12) A finite set A∈ NαcO(X) if and only if for all x∈A there exists Nαc –open set B such that x∈B
Nαc int(B).(iii) If A is Nαc – open set then, A = Nαc int(A). Proof: Obvious. Corollary (3.12) A finite set A∈ NαcO(X) if and only if for all x∈A there exists Nαc –open set B such that x∈B 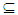 A.Proof: Let A= {x1,x2,..., xn}, suppose there exists Bi∈ NαcO(X) such that xi∈ Bi
A.Proof: Let A= {x1,x2,..., xn}, suppose there exists Bi∈ NαcO(X) such that xi∈ Bi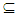 A, this implies
A, this implies 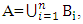 thus by Proposition (3.9) A∈NαcO(X). Conversely; suppose A∈NαcO(X), hence by Proposition (3.11 (iii)), A= Nαc int(A), thus the proof is complete. The intersection of two Nαc –open sets need not be Nαc-open set. See the next example: Example (3.13) Consider X={a,b,c,d} with
thus by Proposition (3.9) A∈NαcO(X). Conversely; suppose A∈NαcO(X), hence by Proposition (3.11 (iii)), A= Nαc int(A), thus the proof is complete. The intersection of two Nαc –open sets need not be Nαc-open set. See the next example: Example (3.13) Consider X={a,b,c,d} with 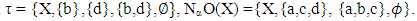 We have A={a,c,d}, B={a,b,c} are Nαc-open sets, but their intersection {a,c} is not Nαc- open set since {a,c} is not Nα- open set. Proposition (3.14) If the collection of all NαO(X) sets is form a topology on X, then NαcO(X) is also. Proof: We shall prove only the finite intersection of NαcO(X) is also. Let A, B∈ NαcO(X), then A,B∈ NαO(X) so, A
We have A={a,c,d}, B={a,b,c} are Nαc-open sets, but their intersection {a,c} is not Nαc- open set since {a,c} is not Nα- open set. Proposition (3.14) If the collection of all NαO(X) sets is form a topology on X, then NαcO(X) is also. Proof: We shall prove only the finite intersection of NαcO(X) is also. Let A, B∈ NαcO(X), then A,B∈ NαO(X) so, A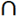 B∈ NαO(X). Suppose x∈ A
B∈ NαO(X). Suppose x∈ A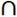 B, this implies x∈ A, x∈ B, then there exist closed sets E and F such that x∈E
B, this implies x∈ A, x∈ B, then there exist closed sets E and F such that x∈E 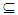 A, x∈F
A, x∈F 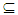 B this implies x∈ E
B this implies x∈ E 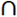 F
F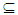 A
A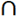 B. Thus A
B. Thus A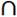 B∈ NαcO(X). Definition (3.15) Let A
B∈ NαcO(X). Definition (3.15) Let A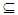 X. The intersection of all Nαc – closed sets containing A is called Nαc – closure of A briefly Nαc cl(A).Proposition (3.16)Let X be a space, A
X. The intersection of all Nαc – closed sets containing A is called Nαc – closure of A briefly Nαc cl(A).Proposition (3.16)Let X be a space, A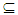 B
B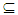 X. Then;(i)
X. Then;(i) 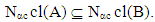 (ii) If A is Nαc – closed set then A= Nαc cl(A). If X is a finite set then, A is Nαc – closed set if and only if A = Nαc cl(A). Proof: Obvious. Proposition (3.17)Let A be a set of a space X. Then, x∈ Nαccl(A) if and only if
(ii) If A is Nαc – closed set then A= Nαc cl(A). If X is a finite set then, A is Nαc – closed set if and only if A = Nαc cl(A). Proof: Obvious. Proposition (3.17)Let A be a set of a space X. Then, x∈ Nαccl(A) if and only if 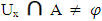 for each Nαc- open set Ux containing x. Proof: Suppose that
for each Nαc- open set Ux containing x. Proof: Suppose that 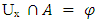 for some Ux∈ NαcO(X) this implies
for some Ux∈ NαcO(X) this implies 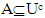 where Uc∈ NαcC(X) not containing x this implies x ∉ Nαccl(A) which is a contradiction to hypothesis. Thus
where Uc∈ NαcC(X) not containing x this implies x ∉ Nαccl(A) which is a contradiction to hypothesis. Thus 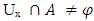 for any Ux∈ NαcO(X). Conversely is a similarly. Proposition (3.18)Every regular closed set is Nαc – open. Proof: Suppose that
for any Ux∈ NαcO(X). Conversely is a similarly. Proposition (3.18)Every regular closed set is Nαc – open. Proof: Suppose that 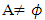 is regular closed so it is closed set since
is regular closed so it is closed set since 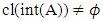 then
then 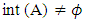 where int(A) is an α – open set hence A∈ NαO(X), thus by Corollary (3.4) A∈ NαcO(X). Lemma (3.19) [14]Let X1, X2, be topological spaces. Then A1, A2, are Nα - open sets in X1, X2 respectively if and only if A1 × A2 is Nα - open set in X1×X2. Proposition (3.20)Let X1, X2 be topological spaces. Then A1, A2, are Nαc - open sets in X1, X2 respectively if and only if A1 × A2 is Nαc - open set in X1× X2. Proof: Assume A1, A2∈ Nαc O(X1), Nαc O(X2) respectively, then by Proposition (3. 2)) A1, A2∈ Nα O(X1), Nα O(X2) respectively hence A1× A2∈ Nα O(X1×X2) see Lemma (3. 19), on the other hand for each X1∈ A1, X2∈ A2 there exist closed sets F1, F2, such that x1∈ F1
where int(A) is an α – open set hence A∈ NαO(X), thus by Corollary (3.4) A∈ NαcO(X). Lemma (3.19) [14]Let X1, X2, be topological spaces. Then A1, A2, are Nα - open sets in X1, X2 respectively if and only if A1 × A2 is Nα - open set in X1×X2. Proposition (3.20)Let X1, X2 be topological spaces. Then A1, A2, are Nαc - open sets in X1, X2 respectively if and only if A1 × A2 is Nαc - open set in X1× X2. Proof: Assume A1, A2∈ Nαc O(X1), Nαc O(X2) respectively, then by Proposition (3. 2)) A1, A2∈ Nα O(X1), Nα O(X2) respectively hence A1× A2∈ Nα O(X1×X2) see Lemma (3. 19), on the other hand for each X1∈ A1, X2∈ A2 there exist closed sets F1, F2, such that x1∈ F1 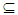 , A1, x2∈ F2
, A1, x2∈ F2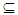 A2. Thus (x1,x2)∈ F1 × F2
A2. Thus (x1,x2)∈ F1 × F2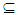 A1×A2, where F1 × F2 is closed set in X1 × X2. Hence A1 × A2∈ Nαc O(X1 × X2). Conversely; if A1 × A2∈ Nαc O(X1 × X2) then, by Proposition (3.2) A1 × A2∈ Nα O(X1 × X2), hence by Lemma (3. 19) A1 ∈ NαO(X1), A2∈ Nα O(X2). On the other hand for each (x1, x2) ∈ A1×A2 there exists closed set F1× F2 in X1 × X2 such that (x1, x2)∈ F1×F2
A1×A2, where F1 × F2 is closed set in X1 × X2. Hence A1 × A2∈ Nαc O(X1 × X2). Conversely; if A1 × A2∈ Nαc O(X1 × X2) then, by Proposition (3.2) A1 × A2∈ Nα O(X1 × X2), hence by Lemma (3. 19) A1 ∈ NαO(X1), A2∈ Nα O(X2). On the other hand for each (x1, x2) ∈ A1×A2 there exists closed set F1× F2 in X1 × X2 such that (x1, x2)∈ F1×F2 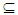 A1×A2, thus x1∈ F1
A1×A2, thus x1∈ F1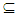 1, x2∈ F2
1, x2∈ F2 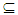 A2, where F1, F2 are closed sets in X1, X2 respectively. Thus A1, A2∈ Nαc O(X1), Nαc O(X2) respectively. Proposition (3.21)Let X1, X2 be topological spaces. Then Nαc cl(A1 × A2) = Nαc cl(A1) × Nαc cl(A2), where A1
A2, where F1, F2 are closed sets in X1, X2 respectively. Thus A1, A2∈ Nαc O(X1), Nαc O(X2) respectively. Proposition (3.21)Let X1, X2 be topological spaces. Then Nαc cl(A1 × A2) = Nαc cl(A1) × Nαc cl(A2), where A1 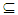 X1, A2
X1, A2 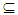 X2. Proof: Let (x1, x2)∈ Nαc cl(A1 × A2), then by Proposition (3. 17)) for each Nαc- - open set in X1×X2 say G=G1 ×G2 containing (x1, x2) then
X2. Proof: Let (x1, x2)∈ Nαc cl(A1 × A2), then by Proposition (3. 17)) for each Nαc- - open set in X1×X2 say G=G1 ×G2 containing (x1, x2) then 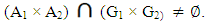 Then
Then 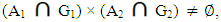 where G1,G2∈NαcO(X1), NαcO(X2) resp., see Proposition (3.20) which means
where G1,G2∈NαcO(X1), NαcO(X2) resp., see Proposition (3.20) which means 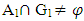 and
and 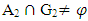 . Thus x1∈ Nαc cl(A1), x2∈ Nαc cl(A2). Hence (x1, x2)∈ Nαc cl(A1) × Nαc cl(A2). Conversely; Let (x1, x2)∈ Nαc cl(A1) × Nαc cl(A2), then x1∈ Nαc cl(A1), x2∈ Nαccl(A2), hence for each Nαc – open sets G1,G2 containing x1, x2 respectively, then
. Thus x1∈ Nαc cl(A1), x2∈ Nαc cl(A2). Hence (x1, x2)∈ Nαc cl(A1) × Nαc cl(A2). Conversely; Let (x1, x2)∈ Nαc cl(A1) × Nαc cl(A2), then x1∈ Nαc cl(A1), x2∈ Nαccl(A2), hence for each Nαc – open sets G1,G2 containing x1, x2 respectively, then 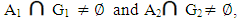 thus
thus 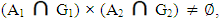 , this implies (A1 × A2)
, this implies (A1 × A2) 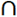 (G1 × G2)
(G1 × G2)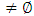 , but G1 ×G2∈ Nαc O(X1 × X2) see Proposition (3. 20). Thus (x1, x2)∈ Nαc cl(A1 × A2). Proposition (3.22) Let Y be a subspace of a space X such that A
, but G1 ×G2∈ Nαc O(X1 × X2) see Proposition (3. 20). Thus (x1, x2)∈ Nαc cl(A1 × A2). Proposition (3.22) Let Y be a subspace of a space X such that A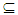 Y
Y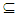 X. Then:-(i) If A∈ NαcO(X) then, A∈ NαcO(Y).(ii) If A∈ NαcO(Y) then, A∈ NαcO(X), where Y is clopen set in X. Proof: (i) Suppose that A∈ NαcO(X), hence A∈ NαO(X), thus by Proposition (2.9) A∈ NαO(Y), let x∈A, hence there
X. Then:-(i) If A∈ NαcO(X) then, A∈ NαcO(Y).(ii) If A∈ NαcO(Y) then, A∈ NαcO(X), where Y is clopen set in X. Proof: (i) Suppose that A∈ NαcO(X), hence A∈ NαO(X), thus by Proposition (2.9) A∈ NαO(Y), let x∈A, hence there 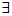 closed set F in X s.t x∈ F
closed set F in X s.t x∈ F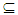 A for each x∈A, hence F is closed in Y, thus A∈ NαcO(Y). (ii) Suppose that A∈ NαcO(Y) hence A∈ NαO(Y) since Y is clopen set in X then by Proposition (2.9) A∈ NαO(X). Let x∈ A, thus
A for each x∈A, hence F is closed in Y, thus A∈ NαcO(Y). (ii) Suppose that A∈ NαcO(Y) hence A∈ NαO(Y) since Y is clopen set in X then by Proposition (2.9) A∈ NαO(X). Let x∈ A, thus 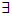 closed set F in Y s.t x∈ F
closed set F in Y s.t x∈ F 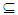 A so F is closed set in X. Thus A∈ NαcO(X). Corollary (3.23) Let Y be a subspace of a space X where A
A so F is closed set in X. Thus A∈ NαcO(X). Corollary (3.23) Let Y be a subspace of a space X where A 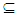 Y
Y 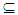 X such that Y is an α - closed set in X then A∈ NαcC(X) if and only if A∈ NαcC(Y)Proof: Follows from Proposition (2.9). Now, we shall discuss the relationships between our concept with some other classes of sets. Remarks (3.24) The following sets are independent with Nαc-open sets (i) Open sets are incomparable with NαcO(X)
X such that Y is an α - closed set in X then A∈ NαcC(X) if and only if A∈ NαcC(Y)Proof: Follows from Proposition (2.9). Now, we shall discuss the relationships between our concept with some other classes of sets. Remarks (3.24) The following sets are independent with Nαc-open sets (i) Open sets are incomparable with NαcO(X)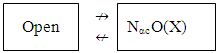 Example (1): Let (R, τu) be the usual topology on real number R, we observe [a,b]∈ NαcO(R) but [a,b]∉ τu. On the other hand every an open set is incomparable with NαO(X), see [14].(ii) Closed sets are incomparable with NαcO(X) i. e
Example (1): Let (R, τu) be the usual topology on real number R, we observe [a,b]∈ NαcO(R) but [a,b]∉ τu. On the other hand every an open set is incomparable with NαO(X), see [14].(ii) Closed sets are incomparable with NαcO(X) i. e 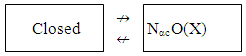 Example (2): In previous example
Example (2): In previous example 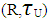 . Assume that A=(0,1] then A∈ NαcO(R) because A∈ NαO(X) see Remark(2.3) so,
. Assume that A=(0,1] then A∈ NαcO(R) because A∈ NαO(X) see Remark(2.3) so, 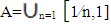 hence A∈ NαcO(X) see Proposition(3.2) but A is not closed set in
hence A∈ NαcO(X) see Proposition(3.2) but A is not closed set in 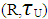 . On the other hand consider X={a,b,c,d} with
. On the other hand consider X={a,b,c,d} with 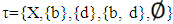 , let A={a,c}, then A is closed set in X but A ∉ NαcO(X) because A ∉ NαO(X). (iii) αOpen sets are incomparable with NαcO(X)
, let A={a,c}, then A is closed set in X but A ∉ NαcO(X) because A ∉ NαO(X). (iii) αOpen sets are incomparable with NαcO(X)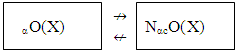 Example (3): See Ex. (2) in (X, τ) let A={a,b,d} then A∈ αO(X) but A ∉ NαcO(X) because A ∉ NαO(X), also if A =[a,b] in (R, τU), then A∈ NαcO(X) but A ∉ αO(X). (iv) Preopen sets are incomparable with NαcO(X)
Example (3): See Ex. (2) in (X, τ) let A={a,b,d} then A∈ αO(X) but A ∉ NαcO(X) because A ∉ NαO(X), also if A =[a,b] in (R, τU), then A∈ NαcO(X) but A ∉ αO(X). (iv) Preopen sets are incomparable with NαcO(X) 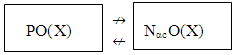 Example (4): See Ex. 2. in (X, τ). Assume that A={b,c,d}, then A∈ PO(X) but A∉ NαcO(X). Also we have A=[a,b] in (R,τU) where A∈ NαcO(X) but A∉ PO(X). (v)
Example (4): See Ex. 2. in (X, τ). Assume that A={b,c,d}, then A∈ PO(X) but A∉ NαcO(X). Also we have A=[a,b] in (R,τU) where A∈ NαcO(X) but A∉ PO(X). (v) 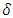 -Open sets are incomparable with NαcO(X)
-Open sets are incomparable with NαcO(X) 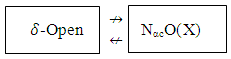 Example (5): In Ex. 2. We notice in (X,τ), if A= {b}, then
Example (5): In Ex. 2. We notice in (X,τ), if A= {b}, then 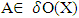 but A∉ NαcO(X). Also if A={a,c,d}, then A∈ NαcO(X) but A∉
but A∉ NαcO(X). Also if A={a,c,d}, then A∈ NαcO(X) but A∉ 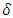 O(X). Proposition (3.25) Let A
O(X). Proposition (3.25) Let A X. Then: (i) If A∈θ O(X), then A∈ NαcO(X). Proof: Follows from Definition of θ – open sets and τ
X. Then: (i) If A∈θ O(X), then A∈ NαcO(X). Proof: Follows from Definition of θ – open sets and τ 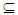 αO(X). (ii) If A is clopen set, then A∈ NαcO(X).Proof: Direct by Remark (2.3) and Corollary (3.4(i)). The converse of (i), (ii) is not true. See the following example: Example 6: See example (2) in Remarks (3.24) of a space X. Suppose that A={a,c,d}. Then A∈ NαcO(X) but it is neither θ - open nor clopen set. Proposition (3.26) Every closed preopen is Nαc-open set. Proof: It follows by Proposition (2.8) and Proposition. (3.25(ii)). From above discussions, we have the following Diagram:
αO(X). (ii) If A is clopen set, then A∈ NαcO(X).Proof: Direct by Remark (2.3) and Corollary (3.4(i)). The converse of (i), (ii) is not true. See the following example: Example 6: See example (2) in Remarks (3.24) of a space X. Suppose that A={a,c,d}. Then A∈ NαcO(X) but it is neither θ - open nor clopen set. Proposition (3.26) Every closed preopen is Nαc-open set. Proof: It follows by Proposition (2.8) and Proposition. (3.25(ii)). From above discussions, we have the following Diagram: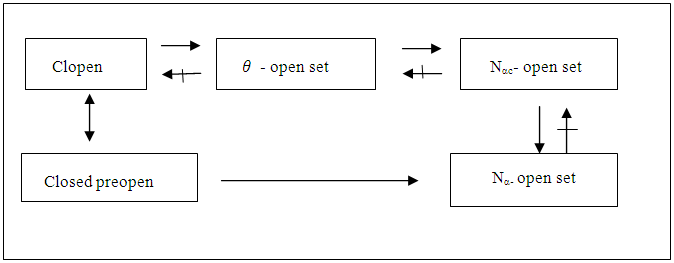 Now, we can prove the converse of previous results such as (3. 2) and (3. 25) are true if we add some conditions. See the next results:-Proposition (3.27)NαcO(X) = NαO(X) where a space X is T1-space.Proof: We show only NαO(X)
Now, we can prove the converse of previous results such as (3. 2) and (3. 25) are true if we add some conditions. See the next results:-Proposition (3.27)NαcO(X) = NαO(X) where a space X is T1-space.Proof: We show only NαO(X) 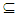 NαcO(X). Assume that A is Nα -open set, let x∈ A then {x} is closed set, thus x∈{x}
NαcO(X). Assume that A is Nα -open set, let x∈ A then {x} is closed set, thus x∈{x}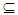 A. Thus A∈ NαcO(X).Proposition (3.28)If a space X is Nα** - regular space. Then we have the following results:-(i) NαO(X) = NαcO(X).(ii) θO(X) = NαcO(X).(iii) CO(X) = NαcO(X) where X is Alexindroff space.(iv) τ= NαcO(X) where X is Locally Indiscrete space.Proof: (i) We have NαcO(X))
A. Thus A∈ NαcO(X).Proposition (3.28)If a space X is Nα** - regular space. Then we have the following results:-(i) NαO(X) = NαcO(X).(ii) θO(X) = NαcO(X).(iii) CO(X) = NαcO(X) where X is Alexindroff space.(iv) τ= NαcO(X) where X is Locally Indiscrete space.Proof: (i) We have NαcO(X)) 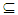 NαO(X). To prove NαO(X)
NαO(X). To prove NαO(X) 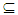 NαcO(X). Let A be Nα-open set, since X is Nα** - regular space then for all x∈ A
NαcO(X). Let A be Nα-open set, since X is Nα** - regular space then for all x∈ A  an open set G s.t x∈ G
an open set G s.t x∈ G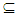 cl(G)
cl(G) 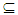 A see Theorem (2.10). Hence A∈NαcO(X) see Proposition (3.2). Thus NαO(X) = NαcO(X).(ii) We have θO(X))
A see Theorem (2.10). Hence A∈NαcO(X) see Proposition (3.2). Thus NαO(X) = NαcO(X).(ii) We have θO(X)) 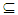 NαcO(X) by Proposition (3.25). Assume A∈ NαcO(X), then A∈ Nα O(X). Since X is Nα**-regular space, then for all x∈ A there exists an open set G such that x∈ G
NαcO(X) by Proposition (3.25). Assume A∈ NαcO(X), then A∈ Nα O(X). Since X is Nα**-regular space, then for all x∈ A there exists an open set G such that x∈ G 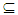 cl(G)
cl(G) 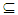 A this implies A∈ θO(X). Thus θO(X)= NαcO(X).(iii) We have every clopen set is Nαc-Open see Proposition (3.25). We shall prove NαcO(X)
A this implies A∈ θO(X). Thus θO(X)= NαcO(X).(iii) We have every clopen set is Nαc-Open see Proposition (3.25). We shall prove NαcO(X) 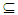 CO(X). Since A∈ NαcO(X), then A∈ NαO(X). Since X is Alexindroof space then by Theorem (2.11) A∈ CO(X). Thus CO(X) = NαcO(X).(v) Suppose that A is nonempty an open set. Since X is Locally Indiscrete space, then A is closed, thus A is clopen set so it is Nα – open set see Remark (2. 3). Thus A∈ NαcO (X) see Corollary (3.4). Let A∈ NαcO (X), then A∈ NαO (X). Since X is Nα ** - regular space, then A is an open set see Theorem (2.11). Hence Nαc O(X) = τ.Proposition (3.29)Each
CO(X). Since A∈ NαcO(X), then A∈ NαO(X). Since X is Alexindroof space then by Theorem (2.11) A∈ CO(X). Thus CO(X) = NαcO(X).(v) Suppose that A is nonempty an open set. Since X is Locally Indiscrete space, then A is closed, thus A is clopen set so it is Nα – open set see Remark (2. 3). Thus A∈ NαcO (X) see Corollary (3.4). Let A∈ NαcO (X), then A∈ NαO (X). Since X is Nα ** - regular space, then A is an open set see Theorem (2.11). Hence Nαc O(X) = τ.Proposition (3.29)Each 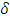 -Open set is Nαc – Open where a space X is Locally Indiscrete.Proof: Suppose that A∈
-Open set is Nαc – Open where a space X is Locally Indiscrete.Proof: Suppose that A∈ 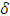 O(X) so it is an open set. We have X is Locally Indiscrete hence A is closed, this implies A is clopen set then by Remark (2. 3) A is Nα - open set, thus by Corollary (3.4) A∈ NαcO(X).Proposition (3.30)NαcO (X)
O(X) so it is an open set. We have X is Locally Indiscrete hence A is closed, this implies A is clopen set then by Remark (2. 3) A is Nα - open set, thus by Corollary (3.4) A∈ NαcO(X).Proposition (3.30)NαcO (X) 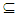
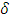 O(X) where X is a discrete space.Proof: Assume that A∈ Nαc O (X), hence A∈ NαO (X) and for all x∈ A there exists closed set F such that x∈ F
O(X) where X is a discrete space.Proof: Assume that A∈ Nαc O (X), hence A∈ NαO (X) and for all x∈ A there exists closed set F such that x∈ F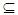 A. Since X is discrete space, then every closed set is an open, this implies x∈ F = cl(F) = int (cl(F)
A. Since X is discrete space, then every closed set is an open, this implies x∈ F = cl(F) = int (cl(F)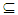 A. Hence A∈
A. Hence A∈ 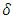 O(X).Proposition (3.31)Each an open set in a regular space X is Nαc-open set.Proof: Let A∈ τ. Since X is a regular space then there exists an open set G such that x∈ G
O(X).Proposition (3.31)Each an open set in a regular space X is Nαc-open set.Proof: Let A∈ τ. Since X is a regular space then there exists an open set G such that x∈ G 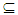 cl(G)
cl(G) 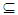 A, for each x∈A. We get cl(G)
A, for each x∈A. We get cl(G) 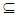 A, where G is an open set so it is an α - open thus A∈ NαO (X) and A=
A, where G is an open set so it is an α - open thus A∈ NαO (X) and A=  cl(G) for each x∈A. Thus by Proposition (3. 2)) A∈ NαcO(X).
cl(G) for each x∈A. Thus by Proposition (3. 2)) A∈ NαcO(X).4. Conclusions
- In this paper we have introduced the notion of Nαc -open sets. Next, some of their basic properties are discussed and studied. Moreover, some relationships between our concepts with some classes of sets are investigated. This new notion will help us to study a new kind of Nαc – continuous mappings and to study a new kind of Nαc – separation axioms.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML