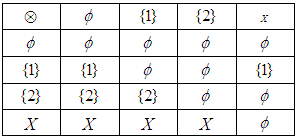-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2018; 8(1): 1-7
doi:10.5923/j.ajms.20180801.01

Soft BCH-Algebras of the Power Sets
Shuker Mahmood Khalil, Mayadah Abd Ulrazaq
Department of Mathematics, College of Science, University of Basrah, Basrah, Iraq
Correspondence to: Shuker Mahmood Khalil, Department of Mathematics, College of Science, University of Basrah, Basrah, Iraq.
| Email: |  |
Copyright © 2018 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, in the first we introduce the concept of 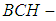 algebra of the power set and new notions connected to it are investigated and discussed like
algebra of the power set and new notions connected to it are investigated and discussed like 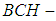 subalgebra of the power set, soft
subalgebra of the power set, soft 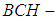 algebra of the power set and soft
algebra of the power set and soft 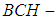 subalgebra of the power set. Then some binary operations between two soft
subalgebra of the power set. Then some binary operations between two soft 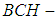 algebras of the power set are studied. Further, we state the relations between soft
algebras of the power set are studied. Further, we state the relations between soft 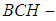 algebra of the power set and soft
algebra of the power set and soft 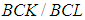
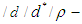 algebra of the power set. Moreover, several examples are given to illustrate the notations introduced in this work.
algebra of the power set. Moreover, several examples are given to illustrate the notations introduced in this work.
Keywords:
Soft sets theory, Proper 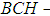 algebra,
algebra, 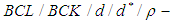 algebras
algebras
Cite this paper: Shuker Mahmood Khalil, Mayadah Abd Ulrazaq, Soft BCH-Algebras of the Power Sets, American Journal of Mathematics and Statistics, Vol. 8 No. 1, 2018, pp. 1-7. doi: 10.5923/j.ajms.20180801.01.
1. Introduction
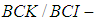 algebras two classes of abstract algebras are introduced by Imai and Iseki ([22], [23]). The class of BCK-algebras is a proper subclass of the class of
algebras two classes of abstract algebras are introduced by Imai and Iseki ([22], [23]). The class of BCK-algebras is a proper subclass of the class of 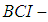 algebras. Also, Hu and Li introduced a wider class of abstract algebras, it is said to be BCH-algebras ([5], [6]). Next, the concept of
algebras. Also, Hu and Li introduced a wider class of abstract algebras, it is said to be BCH-algebras ([5], [6]). Next, the concept of 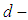 algebras, which is another useful generalization of BCK –algebras are introduced (see [2], [3], [20]). After then, the concept of
algebras, which is another useful generalization of BCK –algebras are introduced (see [2], [3], [20]). After then, the concept of 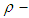 algebra is introduced and studied [9]. The basic notions of soft sets theory are introduced by Molodtsov ([18]) to deal with uncertainties when solving problems in practice as in engineering, social science, environment, and economics. This notion is convenient and easy to apply as it is free from the difficulties that appear when using other mathematical tools as theory of theory of fuzzy sets, rough sets and theory of vague sets etc. Moreover, many researches on soft sets theory and some of their applications are studied (see [10]-[15]). On other word, many authors applied the notion of soft set on several classes of algebras like soft
algebra is introduced and studied [9]. The basic notions of soft sets theory are introduced by Molodtsov ([18]) to deal with uncertainties when solving problems in practice as in engineering, social science, environment, and economics. This notion is convenient and easy to apply as it is free from the difficulties that appear when using other mathematical tools as theory of theory of fuzzy sets, rough sets and theory of vague sets etc. Moreover, many researches on soft sets theory and some of their applications are studied (see [10]-[15]). On other word, many authors applied the notion of soft set on several classes of algebras like soft 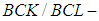 algebras [7] and soft
algebras [7] and soft 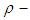 algebras [16]. In recent years, for any
algebras [16]. In recent years, for any 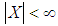 (finite set
(finite set 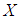 ), the notations of
), the notations of 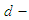 algebra of the power set,
algebra of the power set, 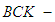 algebra of the power set,
algebra of the power set, 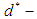 algebra of the power set, soft
algebra of the power set, soft 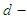 algebra of the power set, soft
algebra of the power set, soft 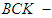 algebra of the power set, soft
algebra of the power set, soft 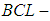 algebra of the power set, soft
algebra of the power set, soft 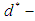 algebra of the power set, soft edge
algebra of the power set, soft edge 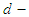 algebra of the power set, soft edge
algebra of the power set, soft edge 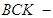 algebra of the power set, soft edge
algebra of the power set, soft edge 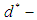 algebra of the power set are introduced (see [16], [17]). The aim of this paper is to introduce new branch of the pure algebra it's called
algebra of the power set are introduced (see [16], [17]). The aim of this paper is to introduce new branch of the pure algebra it's called 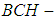 algebra of the power set. Then some binary operations between two soft
algebra of the power set. Then some binary operations between two soft 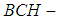 algebras of the power set are stated. Further, we study the relations between soft
algebras of the power set are stated. Further, we study the relations between soft 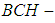 algebra of the power set and soft
algebra of the power set and soft 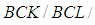
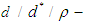 algebra of the power set. Also, several examples are given to illustrate the notations introduced in this work.
algebra of the power set. Also, several examples are given to illustrate the notations introduced in this work.2. Preliminaries
- In this section we recall the basic background needed in our present work.Definition 2.1: ([20]) A
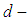 algebra is a non-empty set
algebra is a non-empty set 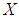 with a constant 0 and a binary operation* satisfying the following axioms:(i)-
with a constant 0 and a binary operation* satisfying the following axioms:(i)- 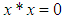 (ii)-
(ii)- 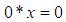 (iii)-
(iii)- 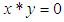 and
and 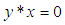 imply that
imply that 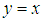 for all x, y in X.Definition 2.2: ([19]) A
for all x, y in X.Definition 2.2: ([19]) A 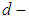 algebra
algebra 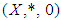 is said to be
is said to be 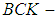 algebra if
algebra if 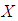 satisfies the following additional axioms:(1).
satisfies the following additional axioms:(1). 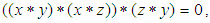 (2).
(2). 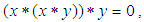 for all
for all 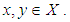 Definition 2.3 ([8]) A
Definition 2.3 ([8]) A 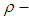 algebra
algebra 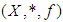 is a non-empty set
is a non-empty set 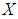 with a constant
with a constant 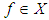 and a binary operation* satisfying the following axioms:(i)-
and a binary operation* satisfying the following axioms:(i)- 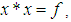 (ii)-
(ii)- 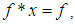 (iii)-
(iii)- 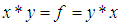 imply that
imply that 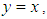 (iv)- For all
(iv)- For all 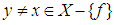 imply that
imply that 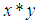
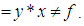 Definition 2.4: ([21]) A
Definition 2.4: ([21]) A 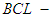 algebra is a non-empty set
algebra is a non-empty set 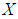 with a constant 0 and a binary operation* satisfying the following axioms:(i)-
with a constant 0 and a binary operation* satisfying the following axioms:(i)- 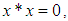 (ii)-
(ii)- 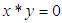 and
and 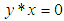 imply that
imply that 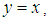 (iii)-
(iii)- 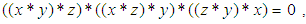 for all x, y ,z in X.Definition 2.4: ([5]) A
for all x, y ,z in X.Definition 2.4: ([5]) A 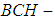 algebra is a non-empty set
algebra is a non-empty set 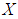 with a constant 0 and a binary operation* satisfying the following axioms:(i)-
with a constant 0 and a binary operation* satisfying the following axioms:(i)- 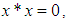 (ii)-
(ii)- 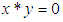 and
and 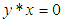 imply that
imply that 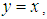 (iii)-
(iii)- 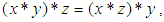 for all x, y ,z in X.Definition 2.5: ([18]) Let
for all x, y ,z in X.Definition 2.5: ([18]) Let 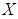 be an initial universe set and let
be an initial universe set and let 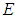 be a set of parameters. The power set of
be a set of parameters. The power set of 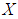 is denoted by
is denoted by 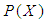 . Let
. Let 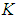 be a subset of
be a subset of 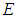 . A pair
. A pair 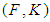 is said to be a soft set over
is said to be a soft set over 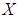 if
if 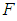 is a set-valued functions of
is a set-valued functions of 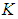 into the set of all subsets of the set
into the set of all subsets of the set 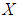 . Definition 2.6: ([11]) Let
. Definition 2.6: ([11]) Let 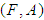 and
and 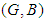 be two soft sets over
be two soft sets over 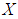 , then their union is the soft set
, then their union is the soft set 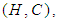 where
where 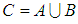 and for all
and for all 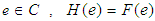 if
if 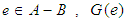 if
if 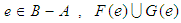 if
if 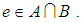 We write
We write 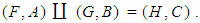 Further, [4] for any two soft sets
Further, [4] for any two soft sets 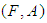 and
and 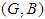 over
over 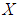 their intersection is the soft set
their intersection is the soft set 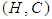 over
over 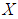 , and we write
, and we write 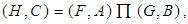 where
where 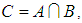 and
and 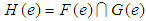 for all
for all 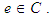 Definition 2.7: ([8]) Let
Definition 2.7: ([8]) Let 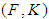 be a soft set over
be a soft set over 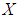 . Then
. Then 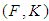 is said to be a soft
is said to be a soft 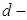 algebra over
algebra over 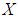 if
if 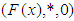 is a
is a 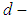 algebra for all
algebra for all 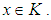 Definition 2.8: ([7]) Let
Definition 2.8: ([7]) Let 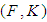 be a soft set over
be a soft set over 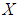 . Then
. Then 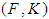 is said to be a soft
is said to be a soft 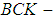 algebra over
algebra over 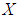 if
if 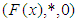 is a
is a 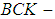 algebra for all
algebra for all 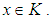 Definition 2.9: ([7]) Let
Definition 2.9: ([7]) Let 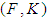 be a soft set over
be a soft set over 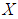 . Then
. Then 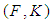 is said to be a soft
is said to be a soft 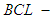 algebra over
algebra over 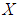 if
if 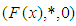 is a
is a 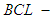 algebra for all
algebra for all 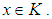 Definition 2.10: ([16]) Let
Definition 2.10: ([16]) Let 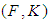 be a soft set over
be a soft set over 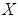 . Then
. Then 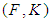 is said to be a soft
is said to be a soft 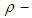 algebra over
algebra over 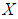 if
if 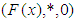 is a
is a  algebra for all
algebra for all 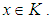 Definition 2.10: ([24]) Let
Definition 2.10: ([24]) Let 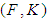 be a soft set over
be a soft set over 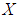 . Then
. Then 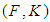 is said to be a soft
is said to be a soft 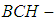 algebra over
algebra over 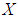 if
if 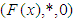 is a
is a 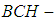 algebra for all
algebra for all  Definition 2.11: ([16]) Let
Definition 2.11: ([16]) Let 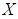 be non-empty set and
be non-empty set and 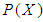 be a power set of
be a power set of 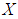 . Then
. Then 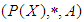 with a constant
with a constant 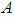 and a binary operation* is said to be
and a binary operation* is said to be 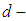 algebra of the power set of
algebra of the power set of 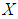 if
if 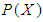 satisfying the following axioms:(i)-
satisfying the following axioms:(i)- 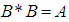 (ii)-
(ii)- 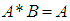 (iii)-
(iii)- 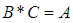 and
and 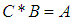 imply that
imply that 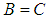 for all
for all 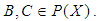 Definition 2.12: ([16]) Let
Definition 2.12: ([16]) Let 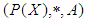 be a
be a 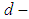 algebra of the power set of
algebra of the power set of 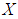 . Then
. Then 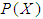 is said to be
is said to be 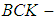 algebra of the power set of
algebra of the power set of 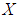 if it satisfies the following additional axioms:(1).
if it satisfies the following additional axioms:(1). 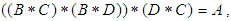 (2).
(2). 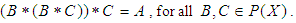 Definition: 2.13: ([16]) Let
Definition: 2.13: ([16]) Let 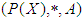 be a
be a 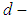 algebra of the power set of
algebra of the power set of 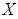 . Then
. Then 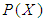 is said to be a
is said to be a 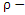 algebra of the power set of
algebra of the power set of 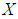 if it satisfies the identity
if it satisfies the identity 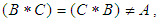 for all
for all 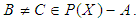 Definition 2.14: ([16]) Let
Definition 2.14: ([16]) Let 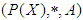 be a
be a 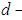 algebra of the power set of
algebra of the power set of 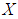 . Then
. Then 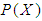 is said to be a
is said to be a 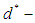 algebra of the power set of
algebra of the power set of 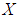 if it satisfies the identity
if it satisfies the identity 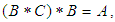 for all
for all 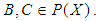 Definition 3.1: ([17]) Let
Definition 3.1: ([17]) Let 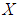 be non-empty set and
be non-empty set and 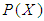 be a power set of
be a power set of 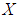 . Then
. Then 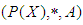 with a constant
with a constant 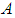 and a binary operation
and a binary operation 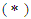 is said to be
is said to be 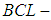 algebra of the power set of
algebra of the power set of 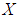 if
if 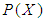 satisfying the following axioms:(i)-
satisfying the following axioms:(i)- 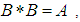 (ii)-
(ii)- 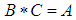 and
and 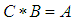 imply that
imply that 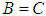 for all
for all 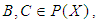 (iii)-
(iii)- 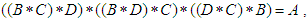 for all
for all 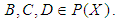 Definition 2.15: ([16], [17]) Let
Definition 2.15: ([16], [17]) Let 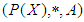 be a
be a 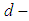 algebra
algebra 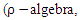
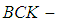 algebra,
algebra, 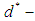 algebra,
algebra, 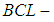 algebra) of the power set of
algebra) of the power set of 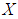 and let
and let 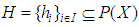 be a collection of some random subsets of
be a collection of some random subsets of 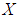 . Then
. Then 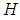 is said to be
is said to be 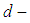 subalgebra (resp.
subalgebra (resp. 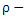 subalgebra,
subalgebra, 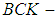 subalgebra,
subalgebra, 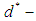 subalgebra,
subalgebra, 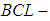 subalgebra) of the power set of
subalgebra) of the power set of 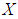 , if
, if 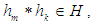 for any
for any 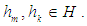 Definition 2.16: ([16], [17]) Let
Definition 2.16: ([16], [17]) Let 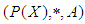 be a
be a 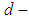 algebra (resp.
algebra (resp. 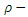 algebra,
algebra, 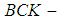 algebra,
algebra, 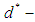 algebra,
algebra, 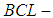 algebra) of the power set of
algebra) of the power set of 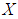 and let
and let 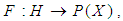 be a set valued function , where
be a set valued function , where 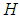 is a collection of some random subsets of
is a collection of some random subsets of 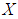 defined by
defined by 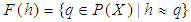 for all
for all 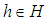 where
where 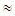 is an arbitrary binary operation from
is an arbitrary binary operation from 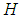 to
to 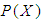 . Then the pair
. Then the pair 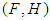 is a soft set over
is a soft set over 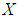 . Further,
. Further, 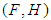 is said to be a soft
is said to be a soft 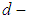 algebra (resp. soft ρ-algebra, soft
algebra (resp. soft ρ-algebra, soft 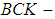 algebra, soft
algebra, soft 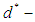 algebra, soft
algebra, soft 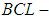 algebra) of the power set of
algebra) of the power set of 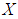 , if
, if 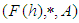 is a
is a 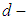 subalgebra (resp.
subalgebra (resp. 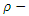 subalgebra,
subalgebra, 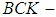 subalgebra,
subalgebra, 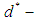 subalgebra,
subalgebra, 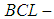 subalgebra) of the power set of
subalgebra) of the power set of 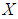 for all
for all 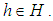
3. Soft BCH-algebra of the Power Sets
- In this section we introduce the notion of soft
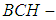 algebra of the power set and soft
algebra of the power set and soft 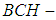 subalgebra of the power set. We will illustrate the definitions with examples.Definition 3.1 Let
subalgebra of the power set. We will illustrate the definitions with examples.Definition 3.1 Let 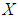 be non-empty set and
be non-empty set and 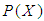 be a power set of
be a power set of 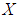 . Then
. Then 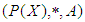 with a constant
with a constant 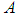 and a binary operation
and a binary operation 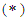 is said to be
is said to be 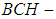 algebra of the power set of
algebra of the power set of 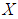 if
if 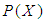 satisfying the following axioms:(i)-
satisfying the following axioms:(i)- 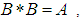 (ii)-
(ii)- 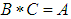 and
and 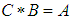 imply that
imply that 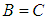 for all
for all 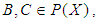 (iii)-
(iii)- 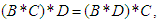 for all
for all 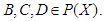 Definition 3.2 A
Definition 3.2 A 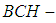 algebra of power set is said to be proper
algebra of power set is said to be proper 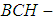 algebra of power set if it satisfies
algebra of power set if it satisfies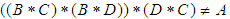 , for some
, for some 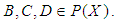 Example 3.3 Let
Example 3.3 Let 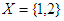 and let
and let 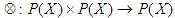 be a binary operation defined by the following table:
be a binary operation defined by the following table:
|
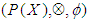 is a proper
is a proper 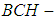 algebra of the power set of
algebra of the power set of 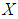 , since there are
, since there are 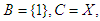
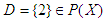 such that
such that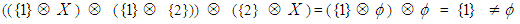 Definition 3.4 Let
Definition 3.4 Let 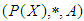 be a
be a 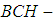 algebra of the power set of
algebra of the power set of 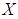 and let
and let 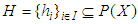 be a collection of some random subsets of
be a collection of some random subsets of 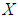 . Then
. Then 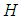 is said to be
is said to be 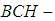 subalgebra of the power set of
subalgebra of the power set of 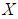 , if
, if 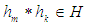 , for any
, for any 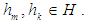 Example 3.5 Let
Example 3.5 Let 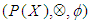 be
be 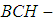 algebra of the power set of
algebra of the power set of 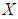 in example (3.3). Then
in example (3.3). Then 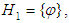
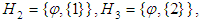
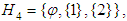
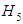
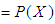 are
are 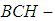 subalgebra of the power set of
subalgebra of the power set of 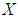 .Remark 3.6 we will show that not necessary every
.Remark 3.6 we will show that not necessary every 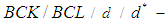 algebra of the power set is
algebra of the power set is 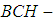 algebra of the power set.Example 3.7 Let
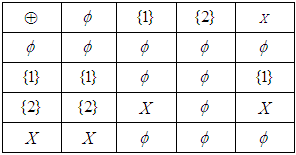
algebra of the power set.Example 3.7 Let 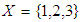 and let
and let 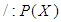
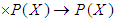 be a binary operation defined by
be a binary operation defined by 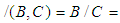
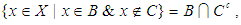 for all
for all 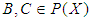 . Then
. Then 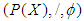 is a
is a 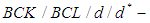 algebra of the power set of
algebra of the power set of 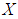 with the following table (2).In other word,
with the following table (2).In other word, 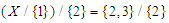
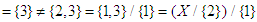 , for some
, for some 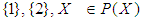 . Then
. Then 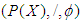 is not
is not 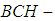 algebra. Also, for example,
algebra. Also, for example, 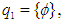
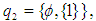
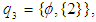
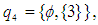
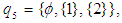
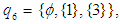 and
and 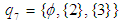 are
are 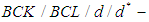 subalgebra of the power set of
subalgebra of the power set of 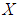 , but not
, but not 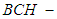 subalgebra. Example 3.8: Let
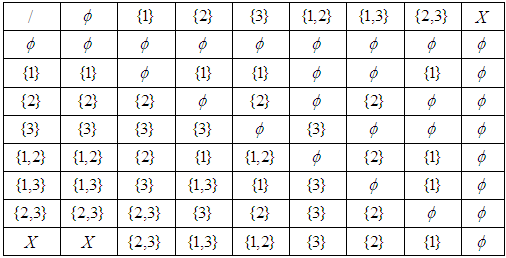
subalgebra. Example 3.8: Let 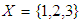 and let
and let 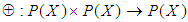 be a binary operation defined by
be a binary operation defined by 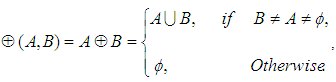 for all
for all 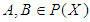 . Then
. Then 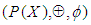 is a
is a 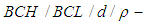 algebra of the power set of
algebra of the power set of  with the following table (3).
with the following table (3).
|
|
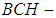 algebra of the power set of
algebra of the power set of 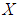 is
is 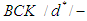 algebra of the power set. In example (3.8), let
algebra of the power set. In example (3.8), let 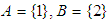 . Then
. Then 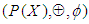 is not
is not 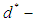 algebra of the power set of
algebra of the power set of 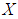 , since
, since 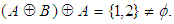 Also, let
Also, let 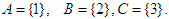 Then
Then 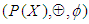 is not
is not 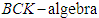 of the power set of
of the power set of 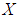 , since
, since 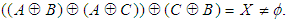 Also,
Also, 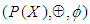 is a
is a 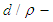 algebra of the power set of
algebra of the power set of 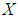 . On the other hand,
. On the other hand, 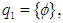
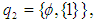
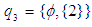 and
and 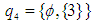 are
are 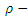 subalgebras. However,
subalgebras. However, 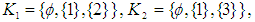 and
and 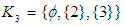 are not
are not 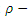 subalgebras. Further, see example (3.7)
subalgebras. Further, see example (3.7) 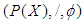 is not ρ-algebra. (2) Further, if
is not ρ-algebra. (2) Further, if 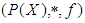 is a
is a 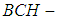 algebra of the power set of
algebra of the power set of 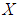 satisfying
satisfying 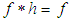 for any
for any 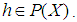 Then
Then 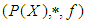 is a d-algebra of the power set of X. Definition 3.10 Let
is a d-algebra of the power set of X. Definition 3.10 Let 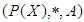 be a
be a 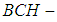 algebra of the power set of
algebra of the power set of 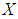 and let
and let 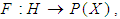 be a set valued function , where
be a set valued function , where 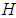 is a collection of some random subsets of
is a collection of some random subsets of 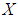 defined by
defined by 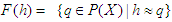 for all
for all 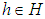 where
where 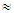 is an arbitrary binary operation from
is an arbitrary binary operation from 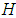 to
to 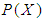 . Then the pair
. Then the pair 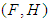 is a soft set over
is a soft set over 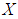 . Further,
. Further, 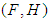 is said to be a soft
is said to be a soft 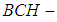 algebra of the power set of
algebra of the power set of 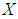 , if
, if 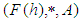 is a
is a 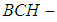 subalgebra of the power set of
subalgebra of the power set of 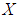 for all
for all 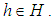 Example: 3.11 Let
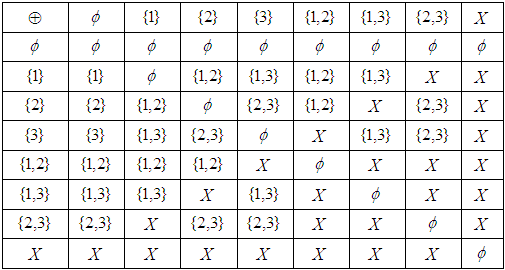
Example: 3.11 Let 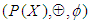 be a proper
be a proper 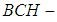 algebra of the power set of
algebra of the power set of 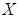 with the following table:
with the following table:
|
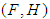 be a soft set over
be a soft set over 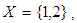 where
where 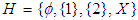 and
and 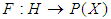 is a set valued function defined by
is a set valued function defined by 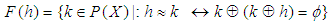 for all
for all 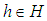 . Then
. Then 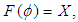
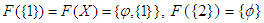 which are soft
which are soft 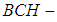 subalgebras of the power set of
subalgebras of the power set of 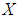 . Hence
. Hence 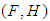 is a soft
is a soft 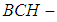 algebra of the power set of
algebra of the power set of 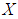 . The next example shows that there exist set-valued functions
. The next example shows that there exist set-valued functions 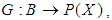 where
where 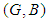 the soft set is not a soft
the soft set is not a soft 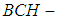 algebra of the power set of
algebra of the power set of 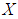 .Example 3.12: Consider the
.Example 3.12: Consider the 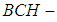 algebra in example (3.11) with a set valued function defined by
algebra in example (3.11) with a set valued function defined by 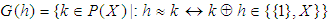 for all
for all 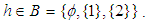 We have
We have 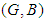 is not a soft
is not a soft 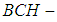 algebra of the power set of
algebra of the power set of 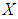 , since there exists
, since there exists 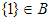 , but
, but 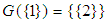 is not soft
is not soft 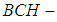 subalgebras of the power set of
subalgebras of the power set of 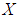 .Definition: 3.13 Let
.Definition: 3.13 Let 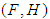 be a soft
be a soft 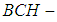 algebra of the power set of
algebra of the power set of 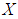 , and let
, and let 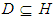 , where
, where 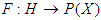 is defined by
is defined by 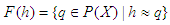 for all
for all 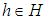 . Then
. Then 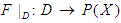 is defined by
is defined by 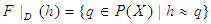 for all
for all 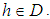 Lemma 3.14: If
Lemma 3.14: If 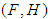 is a soft
is a soft 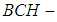 algebra of the power set of
algebra of the power set of 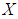 , then
, then 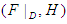 is a soft
is a soft 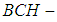 algebra of the power set of
algebra of the power set of 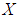 , for any
, for any 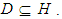 Proof: Let
Proof: Let 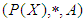 be a
be a 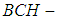 algebra of the power set of
algebra of the power set of 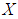 and let
and let 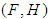 be a soft
be a soft 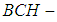 algebra of the power set of
algebra of the power set of 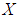 , then
, then 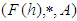 is a
is a 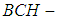 subalgebra of the power set of
subalgebra of the power set of 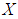 , for all
, for all 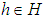 . Moreover, for all
. Moreover, for all 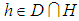 we have
we have 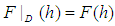 , but
, but 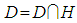 (since
(since 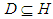 ). Hence
). Hence 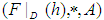 is a
is a 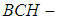 subalgebra of the power set of
subalgebra of the power set of 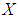 , for all
, for all 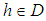 . Then
. Then 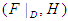 is a soft
is a soft 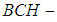 algebra of the power set of
algebra of the power set of 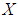 .Definition 3.15: Let
.Definition 3.15: Let 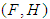 be a soft
be a soft 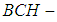 algebra of the power set of
algebra of the power set of  . Then
. Then 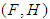 is said to be a null soft
is said to be a null soft 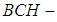 algebra of the power set of
algebra of the power set of 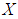 if
if 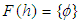 for all
for all 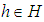 . Also,
. Also, 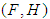 is said to be an absolutely soft
is said to be an absolutely soft 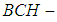 algebra of the power set of
algebra of the power set of 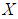 if
if 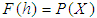 for all
for all 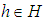 .Example 3.16 Let
.Example 3.16 Let 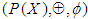 be the
be the 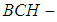 algebra of the power set of
algebra of the power set of 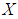 in example (3.11) and let
in example (3.11) and let 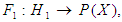
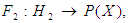 where
where 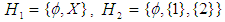 are defined by
are defined by 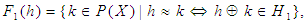
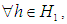 and
and 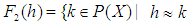
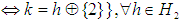 . Thus,
. Thus, 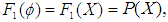 and hence
and hence 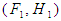 is an absolutely soft
is an absolutely soft 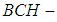 algebra of the power set
algebra of the power set 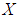 . Moreover,
. Moreover, 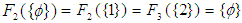 and hence
and hence 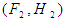 is a null soft
is a null soft 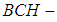 algebra of the power set
algebra of the power set 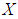 .Lemma: 3.17 Let
.Lemma: 3.17 Let 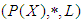 be a
be a 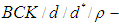 algebra of the power set of
algebra of the power set of 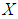 . Then
. Then 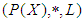 is a
is a  algebra of the power set of
algebra of the power set of 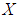 , if
, if 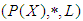 is a
is a 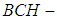 algebra of the power set of
algebra of the power set of 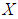 . Proof: Since
. Proof: Since 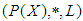 is a
is a 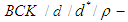 algebra of the power set of
algebra of the power set of 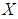 . Then
. Then 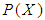 satisfying the following axioms:(i)-
satisfying the following axioms:(i)- 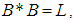 (ii)-
(ii)- 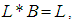 (iii)-
(iii)- 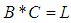 and
and 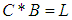 imply that
imply that 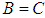 for all
for all 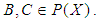 Also, let
Also, let 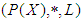 be a
be a 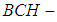 algebra of the power set of
algebra of the power set of 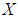 , then
, then 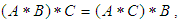 for all. Hence, from (i) we consider that
for all. Hence, from (i) we consider that 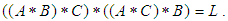 Further, from (ii) we have
Further, from (ii) we have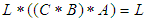 and this implies that
and this implies that 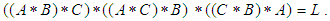 Therefore, the following are hold:(1)-
Therefore, the following are hold:(1)- 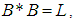 (2)-
(2)- 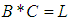 and
and 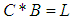 imply that
imply that 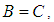 (3)-
(3)- 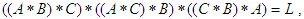 for all
for all 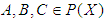 . The
. The 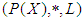 is a
is a 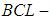 algebra of the power set of
algebra of the power set of 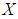 .Corollary 3.18 If
.Corollary 3.18 If 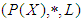 is a
is a 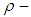 algebra of the power set of
algebra of the power set of 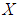 . Then
. Then 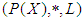 is a
is a 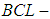 algebra of the power set of
algebra of the power set of 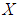 , if
, if 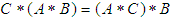 and
and 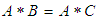 for all
for all 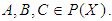 Proof: Since
Proof: Since  is a
is a 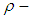 algebra of the power set of
algebra of the power set of 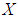 . Then
. Then 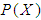 satisfying the following axioms:(i)-
satisfying the following axioms:(i)- 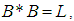 (ii)-
(ii)- 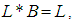 (iii)-
(iii)- 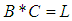 and
and 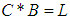 imply that
imply that 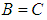 , for all
, for all 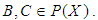 (iv)-
(iv)- 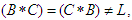 for all
for all 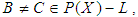 Therefore, we consider only the following are hold:1)-
Therefore, we consider only the following are hold:1)- 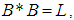 2)-
2)- 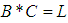 and
and 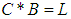 imply that
imply that 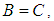 Then, to prove that
Then, to prove that 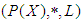 is a
is a 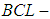 algebra of the power set of
algebra of the power set of 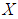 , we need also to prove that
, we need also to prove that 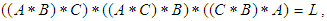 for any
for any 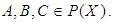 Thus we have to show that
Thus we have to show that 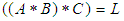 and hence we have
and hence we have 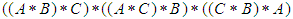
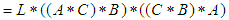
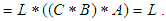 For any
For any 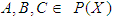 we have the all cases that are cover all probabilities as following:(1) If
we have the all cases that are cover all probabilities as following:(1) If 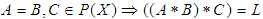 .(2) If
.(2) If 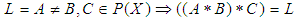 .(3) If
.(3) If 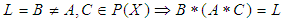 , but
, but 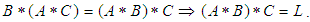 (4) If
(4) If 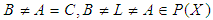 , then
, then 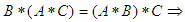
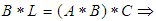
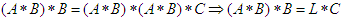
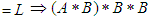
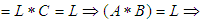
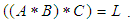 Hence, for all (1),(2),(3), and (4) we consider that
Hence, for all (1),(2),(3), and (4) we consider that 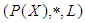 is a
is a  algebra of the power set of
algebra of the power set of  , since
, since 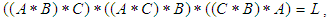 for any
for any 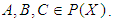 (5) If
(5) If 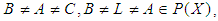 thus since
thus since 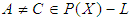 and
and 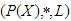 is a
is a 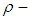 algebra of the power set of
algebra of the power set of 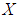 . Then from (iv) we have
. Then from (iv) we have 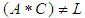 and this implies that
and this implies that 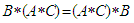 and hence
and hence 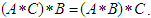 Then
Then 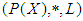 is a
is a 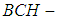 algebra of the power set of
algebra of the power set of 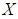 and by[Lemma (3.17)] we have
and by[Lemma (3.17)] we have 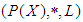 is a
is a 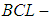 algebra of the power set of
algebra of the power set of 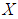 .Remark 3.19 From [Lemma (3.17) and Corollary (3.18)] we consider that, if
.Remark 3.19 From [Lemma (3.17) and Corollary (3.18)] we consider that, if 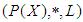 is a
is a 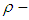 algebra of the power set of
algebra of the power set of 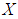 and
and 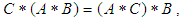 for all
for all 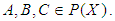 Then
Then 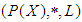 is a
is a 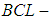 algebra of the power set of
algebra of the power set of 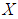 .Theorem 3.20: Let
.Theorem 3.20: Let 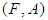 and
and 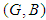 be two soft
be two soft 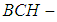 algebras over
algebras over 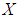 . If
. If 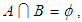 then the union
then the union 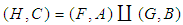 is a soft
is a soft 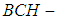 algebra of the power set of
algebra of the power set of 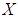 . Proof: Since
. Proof: Since 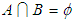 and by definition (2.6), we have for all
and by definition (2.6), we have for all 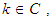
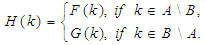 If
If 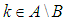 then
then 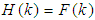 is a
is a  subalgebra of the power set of
subalgebra of the power set of 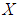 . Similarly, if
. Similarly, if 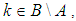 then
then 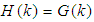 is a
is a 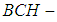 subalgebra of the power set of
subalgebra of the power set of 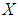 . Hence
. Hence 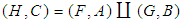 is a soft
is a soft 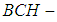 algebra of the power set of
algebra of the power set of 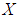 . Thus the union of two soft
. Thus the union of two soft 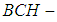 algebras of the power set of
algebras of the power set of 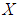 is a soft
is a soft 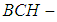 algebra of the power set of
algebra of the power set of 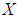 .Example 3.21: In example (3.4), let
.Example 3.21: In example (3.4), let 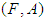 and
and 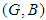 be two soft sets over
be two soft sets over 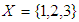 where
where 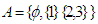 and
and 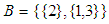 . Define
. Define 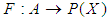 by
by 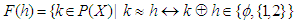 for all
for all 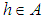 and
and 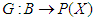 by
by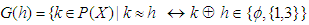 for all
for all 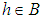 . Note that
. Note that 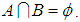 Thus, we have
Thus, we have 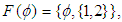
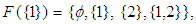
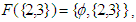
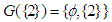 and
and 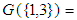
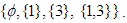 Then
Then 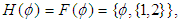
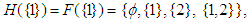
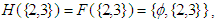
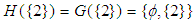 and
and 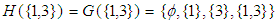 which are
which are 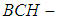 subalgebras of the power set of
subalgebras of the power set of 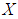 . Hence,
. Hence, 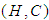 is a soft
is a soft 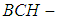 algebra of the power set of
algebra of the power set of 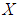 .Remark 3.22: The condition
.Remark 3.22: The condition 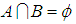 is important as if
is important as if 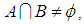 then the theorem does not apply. In above example, if
then the theorem does not apply. In above example, if 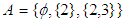 and
and 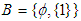 . Then
. Then 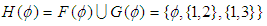 which is not a
which is not a 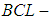 subalgebra of the power set of
subalgebra of the power set of 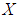 . Therefore, is not a soft
. Therefore, is not a soft 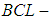 algebra of the power set of
algebra of the power set of 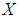 . Theorem 3.23: Let
. Theorem 3.23: Let 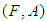 and
and 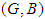 be two soft
be two soft 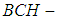 algebras over
algebras over 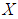 . If
. If 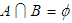 , then the union
, then the union 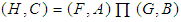 is a soft
is a soft 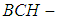 algebra of the power set of
algebra of the power set of 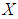 .Proof: Since
.Proof: Since 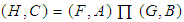 , where
, where 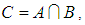 and
and 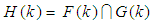 for all
for all 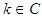 [by definition (2.6)], Note that
[by definition (2.6)], Note that 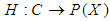 is a mapping and so
is a mapping and so 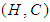 is a soft set over
is a soft set over 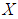 . We have,
. We have, 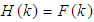 or
or 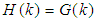 is a
is a 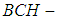 subalgebra of the power set of
subalgebra of the power set of 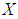 . Hence,
. Hence, 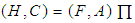
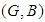 is a soft
is a soft 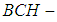 algebra of the power set of
algebra of the power set of 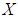 . Therefore, the intersection of two soft
. Therefore, the intersection of two soft 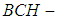 algebras is a soft
algebras is a soft 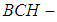 algebra.Example 3.24: Consider the algebra in example (3.21) with
algebra.Example 3.24: Consider the algebra in example (3.21) with 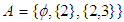 and
and 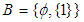 . Then
. Then 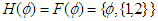 or
or 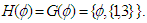 Note that both are
Note that both are 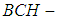 subalgebras of the power set of
subalgebras of the power set of 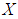 . Hence,
. Hence, 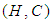 is a soft
is a soft 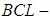 algebras of the power set of
algebras of the power set of 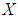 .Theorem 3.25: Let
.Theorem 3.25: Let 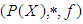 be a
be a 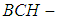 algebra of the power set of
algebra of the power set of 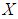 with the condition
with the condition 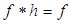 for any
for any 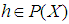 . If
. If 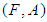 is a soft
is a soft 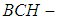 algebra of the power set of
algebra of the power set of 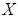 , then
, then 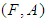 is a soft
is a soft 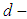 algebra of the power set of
algebra of the power set of 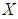 .Proof: Straightforward from Definitions [(3.10), (2.7)] and remark [(2)-(3.9)].Theorem 3.26: Let
.Proof: Straightforward from Definitions [(3.10), (2.7)] and remark [(2)-(3.9)].Theorem 3.26: Let 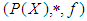 be a
be a 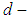 algebra of the power set of
algebra of the power set of 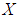 and
and 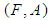 is a soft
is a soft 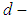 algebra of the power set of
algebra of the power set of 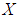 . Then
. Then 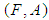 is a soft
is a soft 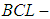 algebra of the power set of
algebra of the power set of 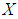 , if
, if 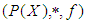 is
is 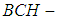 algebra of the power set.Proof: Straightforward from Definitions [(3.10), (2.7)] and [Lemma (3.17)].The author would like to thank from the anonymous reviewers for carefully reading of the manuscript and giving useful comments, which will help to improve the paper.
algebra of the power set.Proof: Straightforward from Definitions [(3.10), (2.7)] and [Lemma (3.17)].The author would like to thank from the anonymous reviewers for carefully reading of the manuscript and giving useful comments, which will help to improve the paper. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML