-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2017; 7(6): 227-236
doi:10.5923/j.ajms.20170706.01

Zero-Truncated Poisson-Akash Distribution and Its Applications
Rama Shanker
Department of Statistics, College of Science, Eritrea Institute of Technology, Asmara, Eritrea
Correspondence to: Rama Shanker, Department of Statistics, College of Science, Eritrea Institute of Technology, Asmara, Eritrea.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, a zero-truncation of Poisson-Akash distribution (PAD) of Shanker (2017) named ‘zero-truncated Poisson-Akash distribution (ZTPAD)’ has been introduced and investigated. A general expression for rth factorial moment about origin has been obtained and hence its raw moments and central moments have been given. The expressions for coefficient of variation, skewness, kurtosis, and the index of dispersion of the distribution have been presented. The method of moments and the method of maximum likelihood estimation have also been discussed for estimating its parameter. Three examples of observed real datasets have been given to test the goodness of fit of ZTPAD over zero-truncated Poisson distribution (ZTPD), zero-truncated Poisson-Lindley distribution (ZTPLD) and zero-truncated Poisson-Sujatha distribution (ZTPSD) and the ZTPAD gives quite satisfactory fit in all datasets.
Keywords: Zero-truncated distribution, Poisson-Akash distribution, Moments, Properties, Estimation of parameter, Goodness of fit
Cite this paper: Rama Shanker, Zero-Truncated Poisson-Akash Distribution and Its Applications, American Journal of Mathematics and Statistics, Vol. 7 No. 6, 2017, pp. 227-236. doi: 10.5923/j.ajms.20170706.01.
Article Outline
1. Introduction
- In probability theory, zero-truncated distributions are certain discrete distributions having support the set of positive integers. Zero-truncated distributions are suitable models for modeling data when the data to be modeled originate from a mechanism which generates data excluding zero counts. Suppose
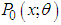 is the original distribution. Then the zero-truncated version of
is the original distribution. Then the zero-truncated version of 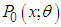 can be defined as
can be defined as 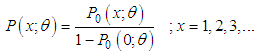 | (1.1) |
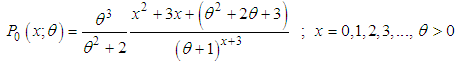 | (1.2) |
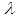 follows Akash distribution introduced by Shanker (2015) with probability density function (pdf)
follows Akash distribution introduced by Shanker (2015) with probability density function (pdf)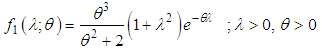 | (1.3) |
2. Zero-Truncated Poisson-Akash Distribution
- Using (1.1) and (1.2), the pmf of zero-truncated Poisson-Akash distribution (ZTPAD) can be obtained as
 | (2.1) |
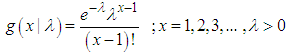 | (2.2) |
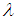 of SBPD follows a continuous distribution having pdf
of SBPD follows a continuous distribution having pdf | (2.3) |
 .The pmf of ZTPAD is thus obtained as
.The pmf of ZTPAD is thus obtained as | (2.4) |
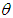 , obtained earlier in (2.1). The main reason for finding the pmf of ZTPAD as a mixture of SBPD with an assumed continuous distribution (2.3) is to obtain the moments easily. The graph of the pmf of ZTPAD for varying values of the parameter
, obtained earlier in (2.1). The main reason for finding the pmf of ZTPAD as a mixture of SBPD with an assumed continuous distribution (2.3) is to obtain the moments easily. The graph of the pmf of ZTPAD for varying values of the parameter 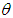 has been shown in figure 1. The graphs show that the pmf is monotonically decreasing for increasing values of the parameter
has been shown in figure 1. The graphs show that the pmf is monotonically decreasing for increasing values of the parameter 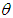 .
.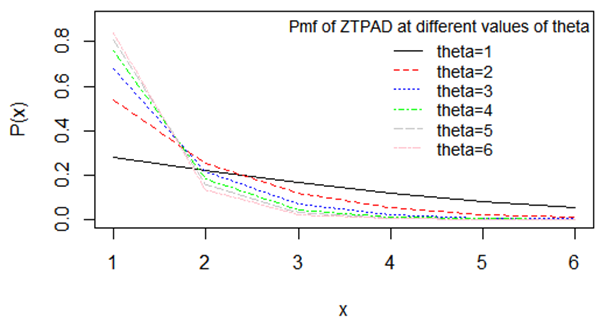 | Figure 1. Graphs of the pmf of ZTPAD for varying values of the parameter θ |
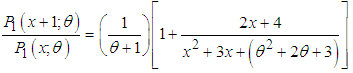 is a decreasing function of x,
is a decreasing function of x, 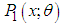 is log-concave. Therefore, ZTPAD is unimodal, has increasing failure rate (IFR), and hence increasing failure rate average (IFRA). It is new better than used (NBU), new better than used in expectation (NBUE), and has decreasing mean residual life (DMRL). Detailed discussions and interrelationships between these aging concepts are available in Barlow and Proschan (1981).Recall that the pmf of zero-truncated Poisson- Lindley distribution (ZTPLD) given by
is log-concave. Therefore, ZTPAD is unimodal, has increasing failure rate (IFR), and hence increasing failure rate average (IFRA). It is new better than used (NBU), new better than used in expectation (NBUE), and has decreasing mean residual life (DMRL). Detailed discussions and interrelationships between these aging concepts are available in Barlow and Proschan (1981).Recall that the pmf of zero-truncated Poisson- Lindley distribution (ZTPLD) given by 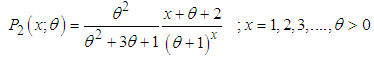 | (2.5) |
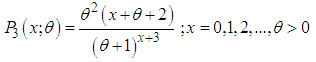 | (2.6) |
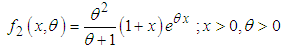 | (2.7) |
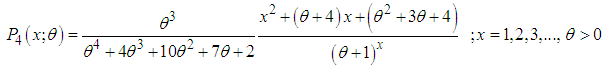 | (2.8) |
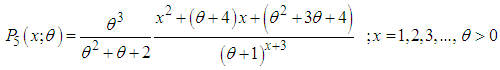 | (2.9) |
 of the Poisson distribution follows Sujatha distribution, introduced by Shanker (2016 a) having pdf
of the Poisson distribution follows Sujatha distribution, introduced by Shanker (2016 a) having pdf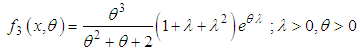 | (2.10) |
3. Moments
- The rth factorial moment about origin of ZTPAD (2.1) can be obtained as
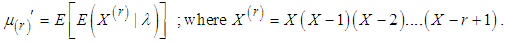 Using (2.4), we have
Using (2.4), we have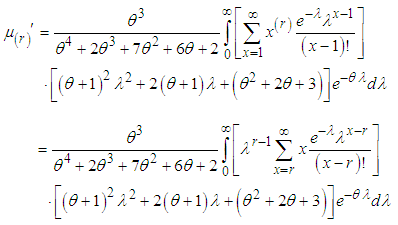 Taking
Taking 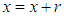 , we get
, we get 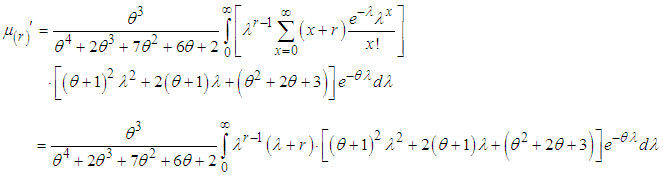 Using gamma integral and a little algebraic simplification, we get the expression for the rth factorial moment about origin of ZTPAD as
Using gamma integral and a little algebraic simplification, we get the expression for the rth factorial moment about origin of ZTPAD as 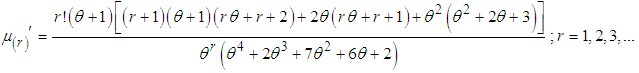 | (3.1) |
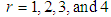 in equation (3.1), the first four factorial moments about origin can be obtained and using the relationship between moments about origin and factorial moments about origin, the first four moments about origin of ZTPAD can be obtained as
in equation (3.1), the first four factorial moments about origin can be obtained and using the relationship between moments about origin and factorial moments about origin, the first four moments about origin of ZTPAD can be obtained as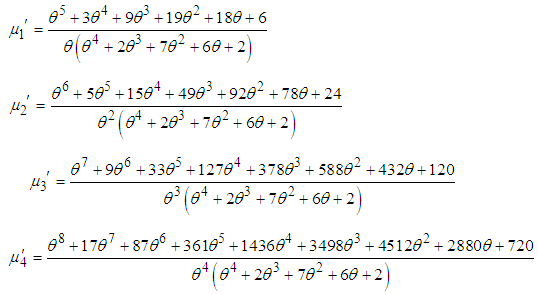 Again using the relationship between moments about origin and central moments, the central moments of ZTPAD are thus obtained as
Again using the relationship between moments about origin and central moments, the central moments of ZTPAD are thus obtained as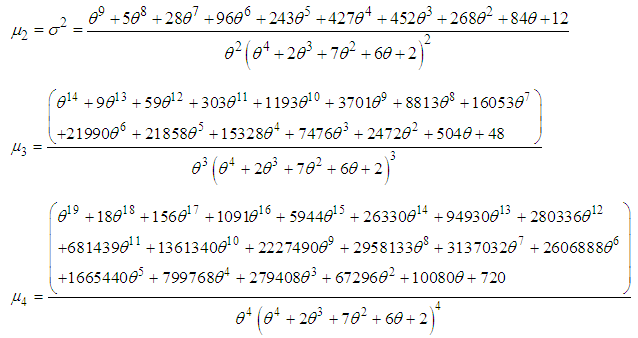 Finally, the coefficient of variation (C.V), coefficient of Skewness
Finally, the coefficient of variation (C.V), coefficient of Skewness 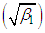 , coefficient of Kurtosis
, coefficient of Kurtosis 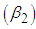 , and index of dispersion
, and index of dispersion 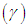 of ZTPAD are obtained as
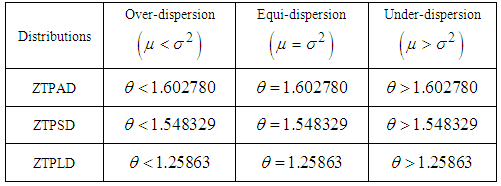
of ZTPAD are obtained as The condition under which ZTPAD is over-dispersed
The condition under which ZTPAD is over-dispersed 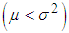 , equi-dispersed
, equi-dispersed 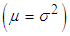 , and under-dispersed
, and under-dispersed 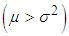 are presented in table 1 along with ZTPSD and ZTPLD.
are presented in table 1 along with ZTPSD and ZTPLD.
|
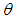 are shown in figure 2. It is obvious that the coefficient of variation and the index of dispersion are monotonically decreasing while the coefficient of skewness and coefficient of kurtosis are monotonically increasing for increasing values of the parameter
are shown in figure 2. It is obvious that the coefficient of variation and the index of dispersion are monotonically decreasing while the coefficient of skewness and coefficient of kurtosis are monotonically increasing for increasing values of the parameter 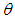 .
.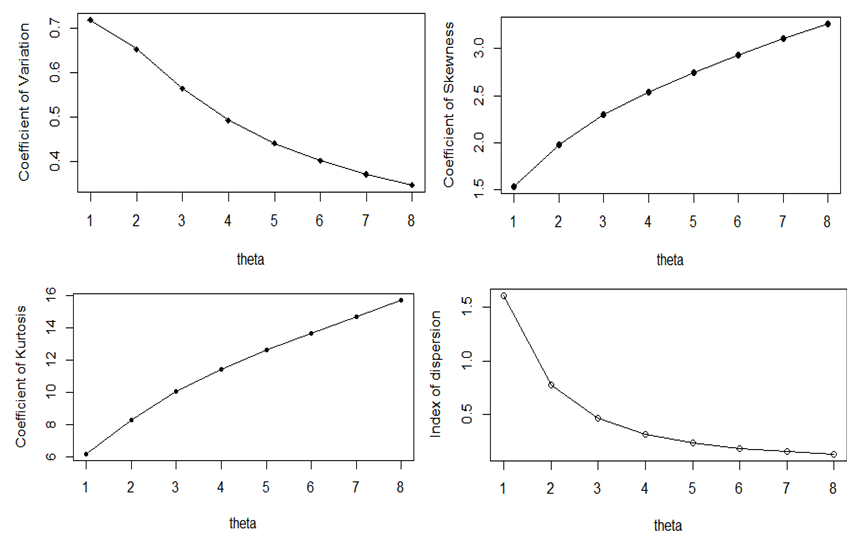 | Figure 2. Graphs of coefficient of variation, coefficient of skewness, coefficient of kurtosis, and index of dispersion of ZTPAD for varying values of the parameter θ |
4. Estimation of Parameter
4.1. Method of Moment Estimate (MOME)
- Let
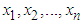 be a random sample of size n from the ZTPAD (2.1). Equating the population mean to the corresponding sample mean, the MOME
be a random sample of size n from the ZTPAD (2.1). Equating the population mean to the corresponding sample mean, the MOME 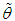 of
of 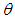 is the solution of the following non-linear equation
is the solution of the following non-linear equation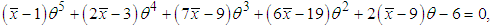 where
where 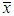 is the sample mean.
is the sample mean.4.2. Maximum Likelihood Estimate (MLE)
- Let
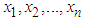 be a random sample of size n from the ZTPAD (2.1) and let
be a random sample of size n from the ZTPAD (2.1) and let 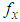 be the observed frequency in the sample corresponding to
be the observed frequency in the sample corresponding to 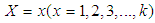 such that
such that 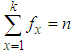 , where k is the largest observed value having non-zero frequency. The likelihood function L of the ZTPAD is given by
, where k is the largest observed value having non-zero frequency. The likelihood function L of the ZTPAD is given by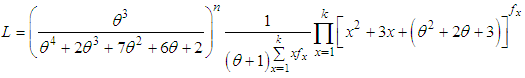 The log likelihood function is given by
The log likelihood function is given by and the log likelihood equation is thus obtained as
and the log likelihood equation is thus obtained as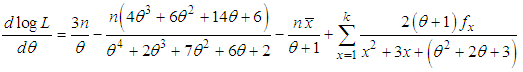 The maximum likelihood estimate
The maximum likelihood estimate 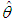 of
of 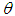 is the solution of the equation
is the solution of the equation 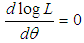 and is given by the solution of the following non-linear equation
and is given by the solution of the following non-linear equation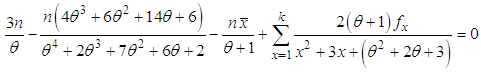 where
where 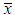 is the sample mean. This non-linear equation can be solved by any numerical iteration methods such as Newton- Raphson method, Bisection method, Regula –Falsi method etc. In this paper Newton-Raphson method has been used to solve the above non-linear equation to estimate the parameter. The initial value of the parameter has been taken from the MOME estimate of the parameter.
is the sample mean. This non-linear equation can be solved by any numerical iteration methods such as Newton- Raphson method, Bisection method, Regula –Falsi method etc. In this paper Newton-Raphson method has been used to solve the above non-linear equation to estimate the parameter. The initial value of the parameter has been taken from the MOME estimate of the parameter.5. Applications
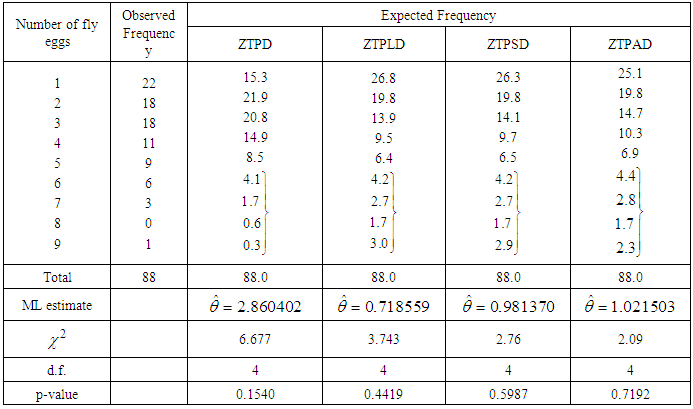
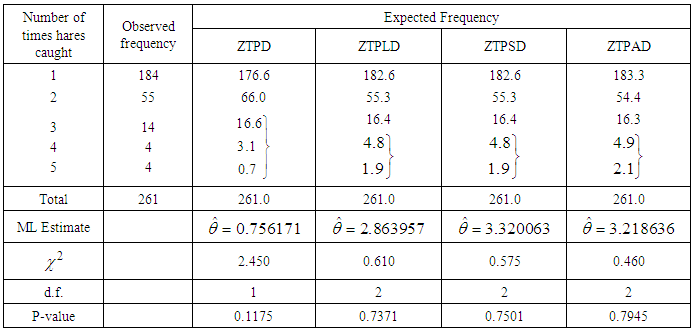
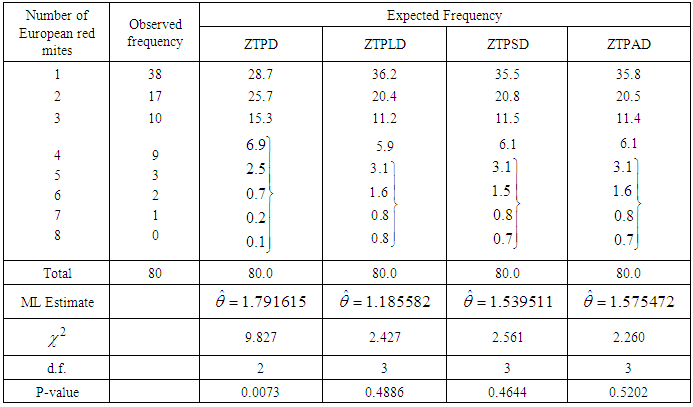
- The ZTPAD has been fitted to a number of real datasets to test its goodness of fit over ZTPD, ZTPLD and ZTPSD and it has been observed that in most cases it gives better fit. Maximum likelihood estimate of the parameter has been used to fit ZTPD, ZTPLD, ZTPSD, and ZTPAD. Here three examples of real datasets have been presented. The dataset in table 2 is the data regarding the number of counts of flower heads as per the number of fly eggs reported by Finney and Varley (1955), the dataset in table 3 is the data regarding the number of snowshoe hares counts captured over 7 days reported by Keith and Meslow (1968) and the dataset in table 4 is the data regarding the number of European red mites on apple leaves reported by Garman (1923). It is obvious from the values of Chi-square
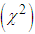 and p-value that ZTPAD gives much closer fit than ZTPD, ZTPLD and ZTPSD. Therefore, ZTPAD can be considered as an important tool for modeling count data excluding zero-count over ZTPD, ZTPLD and ZTPSD.The fitted plots of ZTPD, ZTPLD, ZTPSD and ZTPAD for datasets in tables 2, 3, and 4 have been shown in figure 3 and it is also obvious that ZTPAD gives closer fit in all datasets.
and p-value that ZTPAD gives much closer fit than ZTPD, ZTPLD and ZTPSD. Therefore, ZTPAD can be considered as an important tool for modeling count data excluding zero-count over ZTPD, ZTPLD and ZTPSD.The fitted plots of ZTPD, ZTPLD, ZTPSD and ZTPAD for datasets in tables 2, 3, and 4 have been shown in figure 3 and it is also obvious that ZTPAD gives closer fit in all datasets.
|
|
|
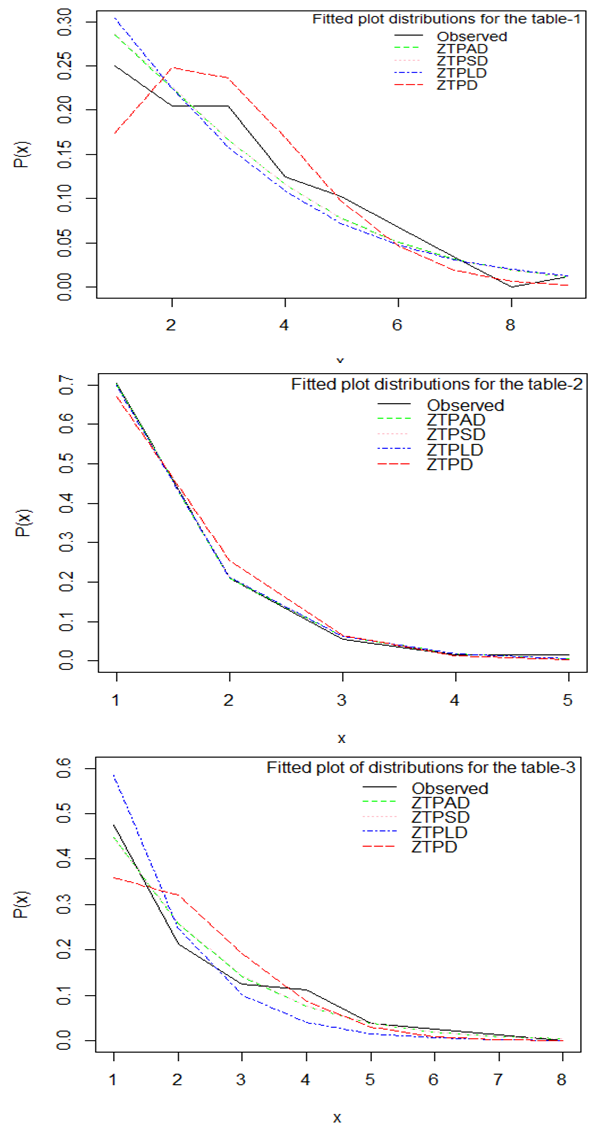 | Figure 3. Fitted plots of ZTPD, ZTPLD, ZTPSD and ZTPAD for datasets in tables 2, 3, and 4 |
6. Concluding Remarks
- A zero-truncated Poisson-Akash distribution (ZTPAD) has been introduced. The general expression for the rth factorial moment about origin has been obtained and thus its raw moments and central moments have been given. The coefficients of variation, skewness, kurtosis, and the index of dispersion of ZTPAD have been obtained. The method of moments and the method of maximum likelihood estimation have been discussed for estimating the parameter of ZTPAD. The goodness of fit of ZTPAD has been discussed with three examples of real datasets and the fit has been compared with ZTPD, ZTPLD and ZTPSD and the fit by ZTPAD has been found to be quite satisfactory. Therefore, ZTPAD can be considered one of the important distributions to model count datasets which structurally excludes zero counts.
ACKNOWLEDGEMENTS
- Author is grateful to the Editor-In-Chief and the anonymous reviewer for fruitful comments on the paper which improved the presentation of the paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML