-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2017; 7(4): 166-168
doi:10.5923/j.ajms.20170704.04

Exhibition of Normal Distribution in Finite p-groups
Adebisi Sunday Adesina, Michael Enioluwafe
Department of Mathematics, University of Ibadan, Ibadan, Nigeria
Correspondence to: Adebisi Sunday Adesina, Department of Mathematics, University of Ibadan, Ibadan, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Suppose that G is a group of order 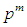 and
and 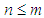 . Let
. Let 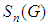 be the number of subgroups of order
be the number of subgroups of order 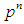 in G. Then, the number of subgroups of order
in G. Then, the number of subgroups of order 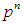 is normally distributed with respect to n, where n is a positive integer.
is normally distributed with respect to n, where n is a positive integer.
Keywords: p-groups, Hall's enumeration principle, Elementary abelian group, Trivial subgroup, Symmetric distribution
Cite this paper: Adebisi Sunday Adesina, Michael Enioluwafe, Exhibition of Normal Distribution in Finite p-groups, American Journal of Mathematics and Statistics, Vol. 7 No. 4, 2017, pp. 166-168. doi: 10.5923/j.ajms.20170704.04.
1. Introduction
- Finite p-groups are ideal objects for combinatorial and cohomological investigations. Some of its basic properties were proved by Sylow, Frobenius, and Burnside. But, namely, Philip Hall (1904-1982) laid the foundations of modern p-group theory (Ber. Y [10]). Normally, Blackburn also made very outstanding achievements after Hall. A common method of investigation in algebra is to break up a complex structure into simpler substructures. The hope is that by repeated application of this procedure, one will eventually arrive at structures that are easy to understand. It may then be possible, in some sense, to synthesis these substructures, so as to reconstruct the original one. While it is rare for the procedure just described to be brought to such a perfect state of completion, the analytic synthetic method can yield valuable information and suggest new concepts. Group theory in general, considers how far this can be used. (Kurosh A.G., 1960) [12]. In this work we examine the basic properties of any p-group which put them in categories and hence define the individual and general characterisations.The hall enumeration principle [10] paves way for counting the subgroups of given structures.Definition: Let p be a prime. A group G is said to be a p-group if the order of every element of G is a power of p. A group which is finite is a p-group if and only if the order of G is a power of p.Remark: (Kuk A.) [13] Let G be a group of order m, and let p be a prime. If
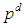 is the highest power of p which divides m, where d is an integer, then the subgroup of order
is the highest power of p which divides m, where d is an integer, then the subgroup of order 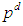 is called a sylow p-subgroup of G.Definition: Elementary Abelian Group: Let G be a p-group. If G is abelian and all its elements (with the exception of the identity) have order p; then, the order of G,
is called a sylow p-subgroup of G.Definition: Elementary Abelian Group: Let G be a p-group. If G is abelian and all its elements (with the exception of the identity) have order p; then, the order of G, 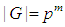 for some
for some 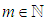 . In this case, G is a direct product of m groups of order p. We then say that G is an elementary abelian p-group.Remark: Two elementary abelian p-groups of the same order
. In this case, G is a direct product of m groups of order p. We then say that G is an elementary abelian p-group.Remark: Two elementary abelian p-groups of the same order 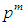 are isomorphic [Ber.Y]. We denote such group by
are isomorphic [Ber.Y]. We denote such group by 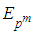 and call it the elementary abelian p-group.Let
and call it the elementary abelian p-group.Let 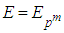 be the elementary abelian group of order
be the elementary abelian group of order 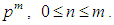 (see [7], [8], [9]). Set
(see [7], [8], [9]). Set 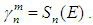 Let
Let 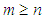 . Then the following assertions are true (see [10], [11]):
. Then the following assertions are true (see [10], [11]):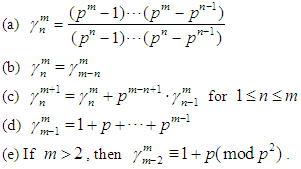 Main ResultThe number of subgroups of order
Main ResultThe number of subgroups of order 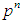 in a finite p-group of order
in a finite p-group of order 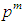 is normally distributed with respect to the positive integer
is normally distributed with respect to the positive integer 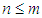 . Hence, by defining a probability function on G, assuming that the area under the graph is a unit, it is possible to estimate the number of subgroups of G.This is one of the main objectives of studying the modern finite p-groups.
. Hence, by defining a probability function on G, assuming that the area under the graph is a unit, it is possible to estimate the number of subgroups of G.This is one of the main objectives of studying the modern finite p-groups.2. Proof of Results
- Definition: Suppose that G is any group such that
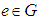 is the identity, then
is the identity, then 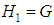 and
and 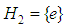 are both subgroups of G called the trivial subgroups of G.By computation, from (a) above, considering simple even and odd cases (for m = 4 & m = 5 respectfully), we have that:(1) For m = 4,
are both subgroups of G called the trivial subgroups of G.By computation, from (a) above, considering simple even and odd cases (for m = 4 & m = 5 respectfully), we have that:(1) For m = 4, 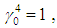 the trivial subgroup of G (the identity).
the trivial subgroup of G (the identity).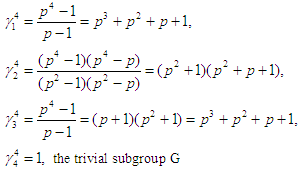 (2) For m = 5
(2) For m = 5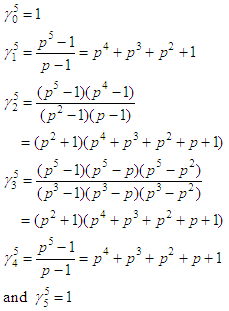 Note here that for m = 4,
Note here that for m = 4,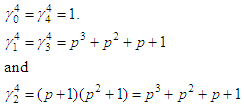 And, for m = 5, we have that
And, for m = 5, we have that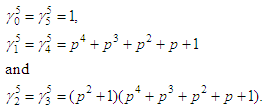 Given that, for
Given that, for 
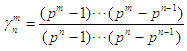 where
where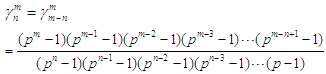 for
for 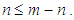 Consider the case:
Consider the case: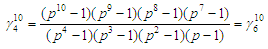 Observe that as n increases from the left (from below),
Observe that as n increases from the left (from below), 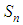 increases to a maximum value at the middle.Also, as n decreases from the right (from above),
increases to a maximum value at the middle.Also, as n decreases from the right (from above), 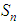 increases in value to the same maximum at the middle. This is seen from the simple computation that:
increases in value to the same maximum at the middle. This is seen from the simple computation that: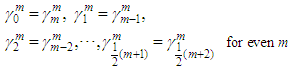 or
or 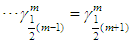 for odd m.Hence, we have the following:Proposition: The limit of
for odd m.Hence, we have the following:Proposition: The limit of 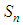 as n increases from below is maximum at
as n increases from below is maximum at 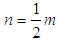 for even m and at
for even m and at 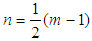 or
or 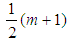 for odd m and we write:
for odd m and we write: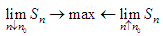 Moreover,
Moreover,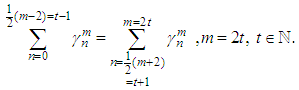 and
and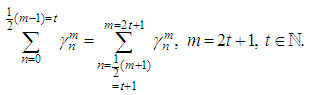 This is a symmetric property.In particular, when m is odd, we ague that
This is a symmetric property.In particular, when m is odd, we ague that 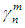 is normally distributed with n, leading to the normal distribution curve.Where the area under the curve indicates the number of subgroups of order
is normally distributed with n, leading to the normal distribution curve.Where the area under the curve indicates the number of subgroups of order 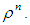
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML