-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2017; 7(4): 152-159
doi:10.5923/j.ajms.20170704.02

Characterizations of ρ-algebra and Generation Permutation Topological ρ-algebra using Permutation in Symmetric Group
Shuker M. Khalil , Marwa Alradha
Department of Mathematics, College of Science, Basra University, Basra, Iraq
Correspondence to: Shuker M. Khalil , Department of Mathematics, College of Science, Basra University, Basra, Iraq.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The aim of this work is to introduce new branch of the pure algebra it's called 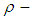 algebra. Further, some new concepts like
algebra. Further, some new concepts like 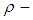 subalgebra,
subalgebra, 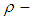 ideal,
ideal, 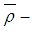 ideal and permutation topological
ideal and permutation topological 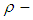 algebra are introduced and studied. It is pointed out that
algebra are introduced and studied. It is pointed out that 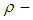 algebra need not be
algebra need not be 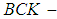 algebra or
algebra or 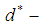 algebra by a counterexample. Moreover, several examples are given to illustrate the concepts introduced in this paper.
algebra by a counterexample. Moreover, several examples are given to illustrate the concepts introduced in this paper.
Keywords:
Cycle type, Permutations, 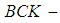 algebra,
algebra, 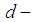 algebra
algebra
Cite this paper: Shuker M. Khalil , Marwa Alradha , Characterizations of ρ-algebra and Generation Permutation Topological ρ-algebra using Permutation in Symmetric Group, American Journal of Mathematics and Statistics, Vol. 7 No. 4, 2017, pp. 152-159. doi: 10.5923/j.ajms.20170704.02.
1. Introduction
- The structure of groups is used in algebra and their orders for finite groups are more important is used in many parts of mathematics, as well as in quantum chemistry and physics. For example Lagrange's theorem [16] about the orders of finite groups are studied to find the number of the solutions of equations in finite groups see ([9]-[11], [13]).
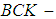 algebra, class of algebra of logic, was introduced by Imai and Iseki [4]. In 1999, the concept of
algebra, class of algebra of logic, was introduced by Imai and Iseki [4]. In 1999, the concept of 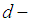 algebras, another generalization of the concept of
algebras, another generalization of the concept of 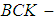 algebras, was introduced by Neggers and Kim [14]. They studied some properties of this class of algebras. Since then many researchers have extensively studied these algebras (see [1]-[3], [5], [18]). In [6], Yonghong Liu introduced a new class of abstract algebra (BCL-algebra) and then he introduced a wide class of abstract algebras (
algebras, was introduced by Neggers and Kim [14]. They studied some properties of this class of algebras. Since then many researchers have extensively studied these algebras (see [1]-[3], [5], [18]). In [6], Yonghong Liu introduced a new class of abstract algebra (BCL-algebra) and then he introduced a wide class of abstract algebras (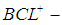 algebra) ([7]). After that some fundamental properties of topological
algebra) ([7]). After that some fundamental properties of topological 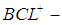 algebras are obtained ([8]).In 2014, the concept of permutation topological space
algebras are obtained ([8]).In 2014, the concept of permutation topological space 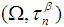 where
where 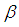 is a permutation in symmetric group
is a permutation in symmetric group 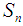 , was introduced by Shuker [12]. The aim of this paper is to introduce new class of algebra it's called
, was introduced by Shuker [12]. The aim of this paper is to introduce new class of algebra it's called 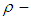 algebra. Also, the relations between
algebra. Also, the relations between 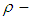 algebra and some algebras like
algebra and some algebras like 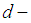 algebra,
algebra, 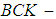 algebra and
algebra and 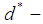 algebra are studied. Further, the concept of
algebra are studied. Further, the concept of 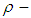 subalgebra is introduced and showed that in
subalgebra is introduced and showed that in 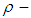 algebra Lagrange's theorem is not true in general. So, there is no law determines the relation between cardinality of
algebra Lagrange's theorem is not true in general. So, there is no law determines the relation between cardinality of 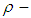 algebra and cardinalities of their
algebra and cardinalities of their 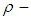 subalgebras. In this work, the notations of
subalgebras. In this work, the notations of 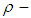 ideal, and
ideal, and 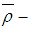 ideal in
ideal in 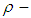 algebra are introduced and investigated their relations with importing types in
algebra are introduced and investigated their relations with importing types in 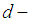 algebra like
algebra like 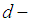 ideal,
ideal, 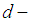 subalgebra and
subalgebra and 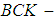 ideal. Further, the multiplication permutation map is given and then a permutation topological
ideal. Further, the multiplication permutation map is given and then a permutation topological 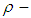 algebra is defined and explained. In another words, permutation topological
algebra is defined and explained. In another words, permutation topological 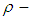 algebra has the algebraic structure of a
algebra has the algebraic structure of a 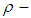 algebra and the permutation topological structure of a topological space and they are linked by the requirement that multiplication permutation is continuous function. Moreover, several examples are given to illustrate the concepts introduced in this paper.
algebra and the permutation topological structure of a topological space and they are linked by the requirement that multiplication permutation is continuous function. Moreover, several examples are given to illustrate the concepts introduced in this paper.2. Preliminaries
- In this section we recall the basic definition and information which are needed in our work.Definition 2.1: [11]A partition
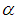 is a sequence of nonnegative integers
is a sequence of nonnegative integers 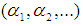 with
with  and
and 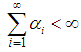 . The length
. The length 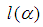 and the size
and the size 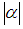 of
of 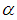 are defined as
are defined as 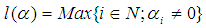 and
and 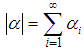 We set
We set 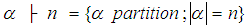 for
for 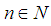 . An element of
. An element of 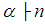 is called a partition of
is called a partition of 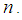 Remark 2.2:We only write the non zero components of a partition. Choose any
Remark 2.2:We only write the non zero components of a partition. Choose any 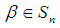 and write it as
and write it as 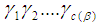 . With
. With 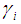 disjoint cycles of length
disjoint cycles of length 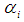 and
and 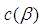 is the number of disjoint cycle factors including the 1-cycle of
is the number of disjoint cycle factors including the 1-cycle of 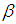 . Since disjoint cycles commute, we can assume that
. Since disjoint cycles commute, we can assume that 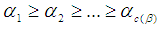 . Therefore
. Therefore 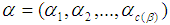 is a partition of
is a partition of 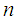 and each
and each 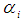 is called part of
is called part of 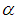 (see [9]).Definition 2.3: [10]We call the partition
(see [9]).Definition 2.3: [10]We call the partition 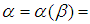
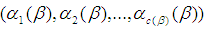 the cycle type of
the cycle type of 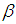 .Definition 2.4: [17] Suppose first that
.Definition 2.4: [17] Suppose first that 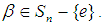 Then
Then 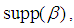 the support of
the support of 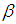 , is the set
, is the set 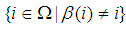 where
where 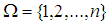 . So we say
. So we say 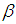 and
and 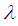 are disjoint cycles iff
are disjoint cycles iff 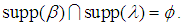 Definition 2.5: [12]Suppose
Definition 2.5: [12]Suppose 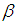 is permutation in symmetric group
is permutation in symmetric group 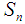 on the set
on the set 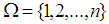 and the cycle type of
and the cycle type of 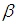 is
is 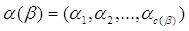 , then
, then 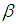 composite of pairwise disjoint cycles
composite of pairwise disjoint cycles 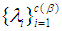 where
where 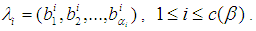 For any
For any 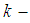 cycle
cycle 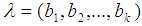 in
in 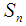 we define
we define 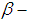 set as
set as 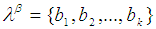 and is called
and is called 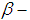 set of cycle
set of cycle 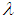 . So the
. So the 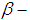 sets of
sets of 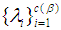 are defined by
are defined by 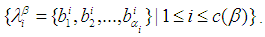 Remark 2.6: [12]For any
Remark 2.6: [12]For any 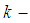 cycle
cycle 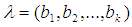 in
in 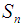 we put
we put 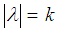 , Further, suppose that
, Further, suppose that 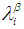 and
and 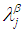 are
are 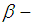 sets in
sets in 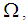 where
where 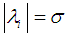 and
and 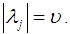 We will give some definitions needed in this work.Definition 2.7: [12]We call
We will give some definitions needed in this work.Definition 2.7: [12]We call 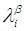 and
and 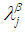 are disjoint
are disjoint 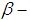 sets in
sets in 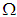 , if and only if
, if and only if 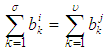 and there exists
and there exists 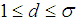 , for each
, for each 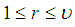 such that
such that 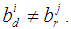 Definition 2.8: [12]We call
Definition 2.8: [12]We call 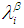 and
and 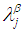 are equal
are equal 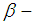 sets in
sets in 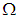 , if and only if for each
, if and only if for each 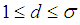 there exists
there exists 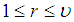 such that
such that 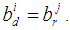 Definition 2.9: [12]We call
Definition 2.9: [12]We call 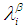 is contained in
is contained in 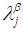 and denoted by
and denoted by 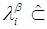
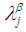 , if and only if
, if and only if 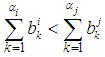 .Definition 2.10: [12]We define the operations
.Definition 2.10: [12]We define the operations 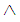 and
and 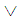 on
on 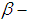 sets in
sets in 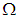 as followers:
as followers: 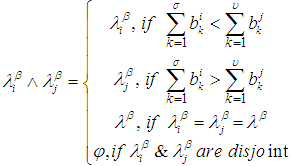 and
and 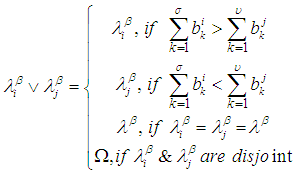 Remarks 2.11: [12]1. The intersection of
Remarks 2.11: [12]1. The intersection of 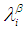 and
and 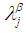 is
is 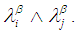 2. The union of
2. The union of 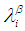 and
and 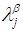 is
is 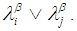 3. The complement of
3. The complement of 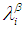 is
is 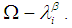 4. The intersection and union of
4. The intersection and union of 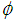 and
and 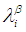 are
are 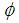 and
and 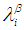 , respectively. 5. The intersection and union of
, respectively. 5. The intersection and union of 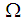 and
and 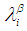 are
are 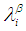 and
and 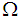 , respectively. Definition 2.12: [12]Let
, respectively. Definition 2.12: [12]Let 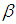 be permutation in symmetric group
be permutation in symmetric group 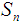 , and
, and 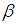 composite of pairwise disjoint cycles
composite of pairwise disjoint cycles 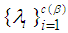 , where
, where 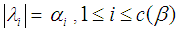 , then
, then 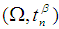 is a permutation topological space where
is a permutation topological space where 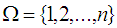 and
and 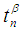 is a collection of
is a collection of 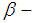 sets of the family
sets of the family 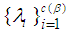 union
union 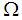 and empty set. Definition 2.13: [12]If
and empty set. Definition 2.13: [12]If 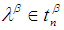 is
is 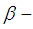 set in the space
set in the space 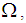 then
then 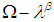 is called closed
is called closed 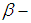 set in the space
set in the space 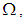 and
and 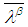 is smallest closed
is smallest closed 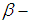 set containing or equal
set containing or equal 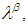 and any
and any 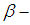 set
set 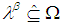 is called closed
is called closed 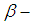 set iff
set iff 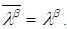 Definition 2.14: [12]The set
Definition 2.14: [12]The set 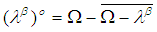 is called the interior of the
is called the interior of the 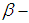 set
set 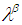 in the permutation space
in the permutation space 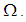 Remarks 2.15: [12]1. We call
Remarks 2.15: [12]1. We call 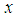 belong to
belong to 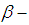 set
set 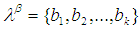 iff
iff 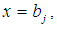 for some
for some 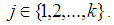 2. The condition
2. The condition 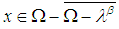 means that
means that 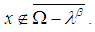 Therefore,
Therefore, 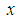 is an interior point of
is an interior point of 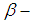 set
set 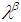 if and only if there is an open
if and only if there is an open 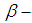 set
set 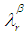 containing
containing 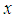 and such that
and such that 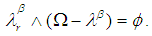 3. If
3. If 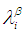 and
and 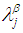 are disjoint
are disjoint 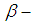 sets in
sets in 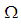 , then neither
, then neither 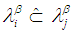 nor
nor 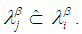 Remark 2.16: [12] Any map between two permutation topological spaces is called permutation map.Definition 2.17: [12]Let
Remark 2.16: [12] Any map between two permutation topological spaces is called permutation map.Definition 2.17: [12]Let 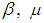 and
and 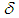 be three permutations in symmetric group
be three permutations in symmetric group 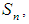 and let
and let 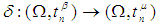 be a function, where for each
be a function, where for each 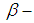 set
set 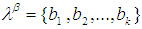 , the image of
, the image of 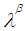 under
under 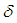 is called
is called 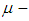 set and defined by the rule
set and defined by the rule 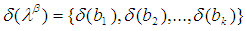 . In another direction, let
. In another direction, let 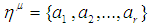 be
be 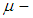 set, the inverse image of
set, the inverse image of 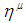 under
under 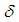 is called
is called 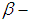 set and defined by the rule
set and defined by the rule 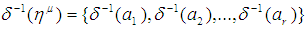 . The usual properties relating images and inverse images of subsets of complements, unions, and intersections also hold for permutation sets. Definition 2.18: [12]Given permutation topological spaces
. The usual properties relating images and inverse images of subsets of complements, unions, and intersections also hold for permutation sets. Definition 2.18: [12]Given permutation topological spaces 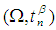 and
and 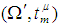 , a function
, a function 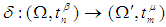 is permutation continuous if the inverse image under
is permutation continuous if the inverse image under 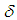 of any open
of any open 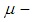 set in
set in 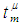 is an open
is an open 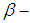 set in
set in 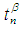 (i.e
(i.e 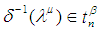 whenever
whenever 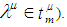 Lemma 2.19: [12]The identity permutation
Lemma 2.19: [12]The identity permutation 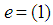 in symmetric group
in symmetric group 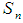 is a permutation continuous on a permutation space
is a permutation continuous on a permutation space 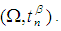 Lemma 2.20: [12]A composition of permutation continuous functions is permutation continuous. Definition 2.21: [14] A
Lemma 2.20: [12]A composition of permutation continuous functions is permutation continuous. Definition 2.21: [14] A 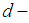 algebra is a non-empty set
algebra is a non-empty set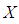 with a constant 0 and a binary operation* satisfying the following axioms:i)-
with a constant 0 and a binary operation* satisfying the following axioms:i)- 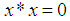 ii)-
ii)- 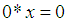 iii)-
iii)- 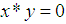 and
and 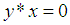 imply that
imply that 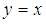 for all x, y in X.Remark 2.22: [14] Let
for all x, y in X.Remark 2.22: [14] Let 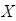 be
be 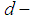 algebra. Then
algebra. Then 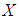 is called finite
is called finite 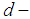 algebra if
algebra if 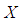 is a finite set.Definition 2.23: [15] A
is a finite set.Definition 2.23: [15] A 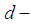 algebra
algebra 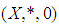 is called
is called  algebra if
algebra if 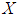 satisfying the following additional axioms:(1).
satisfying the following additional axioms:(1). 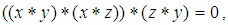 (2).
(2). 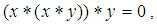 for all
for all 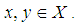 Definition 2.24: [15] Let
Definition 2.24: [15] Let 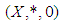 be a
be a 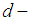 algebra and
algebra and 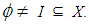 Then I is called a
Then I is called a 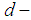 subalgebra of
subalgebra of 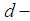 algebra
algebra 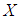 if
if 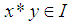 whenever
whenever 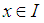 and
and 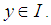 Definition 2.25: [15] Let
Definition 2.25: [15] Let 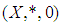 be a
be a 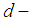 algebra and
algebra and 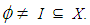 Then I is called a
Then I is called a 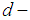 ideal of
ideal of 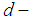 algebra
algebra 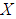 if (1).
if (1). 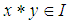 and
and 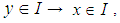 (2).
(2). 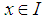 and
and 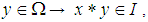 for all
for all 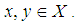 Definition 2.26: [15] Let
Definition 2.26: [15] Let 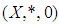 be a
be a 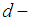 algebra and
algebra and 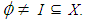 Then I is called a
Then I is called a 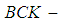 ideal of
ideal of 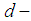 algebra
algebra 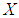 if (1).
if (1). 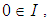 (2).
(2). 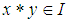 and
and 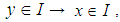 for all
for all 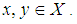 Definition 2.27: [15] Let
Definition 2.27: [15] Let 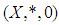 be a
be a 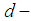 algebra. Then
algebra. Then 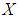 is called a
is called a 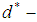 algebra if it satisfies the identity
algebra if it satisfies the identity 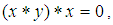 for all
for all 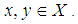 Remark 2.28: [15] In
Remark 2.28: [15] In 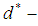 algebra any
algebra any 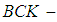 ideal is
ideal is 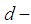 ideal and
ideal and 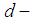 subalgebra.Theorem 2.29: [16] (Lagrange's theorem) Let
subalgebra.Theorem 2.29: [16] (Lagrange's theorem) Let 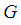 be a finite group and
be a finite group and 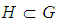 a subgroup of
a subgroup of 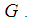 Then
Then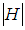 divides
divides 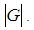 Definition 2.30: [14]: Let
Definition 2.30: [14]: Let 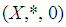 be a
be a 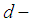 algebra and
algebra and 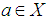 . Define
. Define 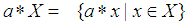 . Then
. Then 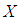 is said to be edge if
is said to be edge if 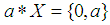 , for all
, for all 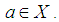
3. Characterizations of ρ-algebra
- Definition 3.1 A
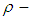 algebra
algebra 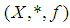 is a non-empty set
is a non-empty set 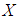 with a constant
with a constant 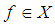 and a binary operation* satisfying the following axioms:i)-
and a binary operation* satisfying the following axioms:i)- 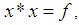 ii)-
ii)- 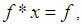 iii)-
iii)- 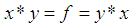 imply that
imply that 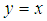 ,iv)- For all
,iv)- For all 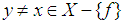 imply that
imply that 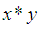
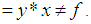 Remark 3.2: It is clear every
Remark 3.2: It is clear every 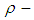 algebra is
algebra is 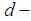 algebra, but the converse is not true in general.Example 3.3: Let
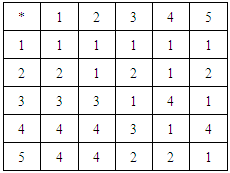
algebra, but the converse is not true in general.Example 3.3: Let 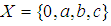 and let the binary operation * be defined as follows:
and let the binary operation * be defined as follows:
|
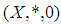 is a
is a 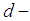 algebra, but not
algebra, but not 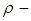 algebra, since there are two elements
algebra, since there are two elements 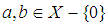 and
and 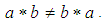 Definition 3.4 Let
Definition 3.4 Let 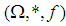 be a
be a 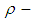 algebra and
algebra and 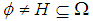 .
. 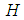 is called a
is called a 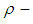 subalgebra of
subalgebra of 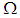 if
if 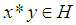 whenever
whenever 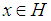 and
and 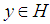 .Theorem 3.5 Let
.Theorem 3.5 Let 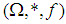 be a
be a 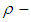 algebra and
algebra and 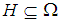 . Then
. Then 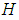 is
is 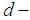 subalgebra of
subalgebra of 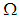 , if
, if 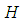 is
is 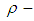 subalgebra of
subalgebra of 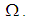 Proof: Suppose that
Proof: Suppose that 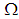 is
is 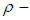 algebra and
algebra and 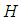 is
is 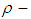 subalgebra of
subalgebra of 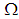 . Then we consider that
. Then we consider that 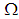 is
is 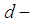 algebra. Also,
algebra. Also, 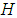 satisfies
satisfies 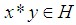 whenever
whenever 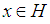 and
and 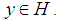 Hence
Hence 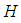 is
is 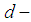 subalgebra of
subalgebra of 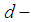 algebra
algebra 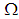 .Remark 3.6 From theorem (3.5) we consider that every
.Remark 3.6 From theorem (3.5) we consider that every  subalgebra is
subalgebra is 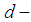 subalgebra. However, the converse is not true in general. Example 3.7 Let
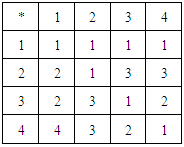
subalgebra. However, the converse is not true in general. Example 3.7 Let 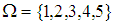 be a
be a 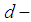 algebra with the following table:
algebra with the following table:
|
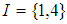 is
is 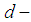 subalgebra of
subalgebra of 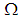 . Further,
. Further, 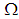 is not
is not 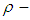 algebra and hence is not
algebra and hence is not 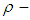 subalgebra of
subalgebra of 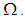 Definition: 3.8For any positive integer
Definition: 3.8For any positive integer 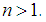 Let
Let 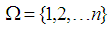 be a finite set and
be a finite set and 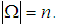 Define binary operation
Define binary operation 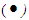 on
on 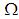 as follows:
as follows: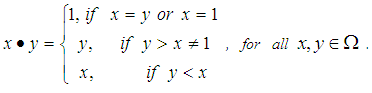 Further, this type of
Further, this type of 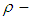 algebra is denoted by
algebra is denoted by 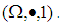 Proposition: 3.9 Let
Proposition: 3.9 Let 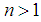 be any positive integer. Then,1)- Each element in
be any positive integer. Then,1)- Each element in 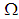 has inverse under the binary operation
has inverse under the binary operation 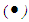 with right identity. 2)- The mathematical system
with right identity. 2)- The mathematical system 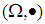 is neither commutative system nor associative system.3)- The mathematical system
is neither commutative system nor associative system.3)- The mathematical system 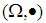 with a constant
with a constant 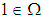 is
is 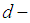 algebra.4)- If
algebra.4)- If 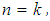 then the number of
then the number of 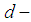 subalgebra or
subalgebra or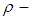 subalgebra of
subalgebra of 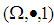 is
is 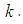 Proof: (1) It is clear for any
Proof: (1) It is clear for any 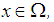 there exists right identity element
there exists right identity element 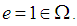 Moreover, for any
Moreover, for any 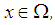 there exists inverse element
there exists inverse element 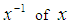 where
where 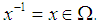 (2) Let
(2) Let 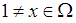 we have
we have 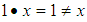
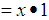 . Then the mathematical system
. Then the mathematical system 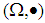 is not a commutative. Now, we need to show that the binary operation
is not a commutative. Now, we need to show that the binary operation 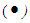 is not associative, let
is not associative, let 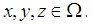 Where
Where 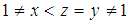
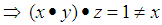
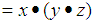 and hence
and hence 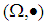 is not associative system. (3) Since
is not associative system. (3) Since 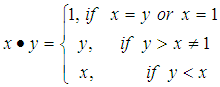 , for all
, for all 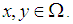 Then for each
Then for each 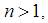 we consider that
we consider that 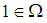 is a constant element and hence the following are hold: i)-
is a constant element and hence the following are hold: i)- 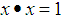 ii)-
ii)- 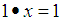 iii)-
iii)- 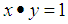 and
and 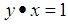 imply that
imply that 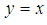 for all
for all 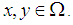 Thus
Thus 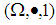 is
is 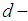 algebra.iv)- For all
algebra.iv)- For all 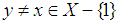 imply that
imply that 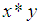
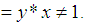 Then
Then  is
is  algebra.4) Let
algebra.4) Let 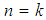 , then for all
, then for all 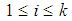 we consider that
we consider that 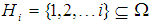 . Also, for any
. Also, for any 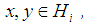
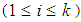 we have
we have 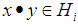 ( by definition 3.4). Then
( by definition 3.4). Then 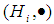 is a
is a 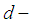 subalgebra and
subalgebra and 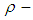 subalgebra of
subalgebra of 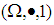 and hence the number of
and hence the number of 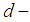 subalgebra or
subalgebra or 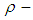 subalgebra of
subalgebra of 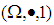 is
is 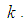 Notations on
Notations on  Algebra Using Type
Algebra Using Type  : 3.10We will show that Lagrange's Theory is also incorrect for finite
: 3.10We will show that Lagrange's Theory is also incorrect for finite 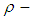 algebra by a counterexample. Let
algebra by a counterexample. Let 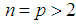 , where
, where 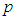 is prime number. Then
is prime number. Then 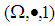 is
is 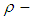 algebra and it is clear that for each
algebra and it is clear that for each 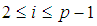 we consider that
we consider that 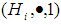 is
is 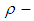 subalgebra of finite
subalgebra of finite 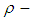 algebra
algebra 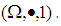 In another side
In another side 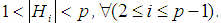 Hence
Hence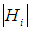 does not divide
does not divide 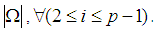 That means in
That means in  algebra Lagrange's theorem is not true in general. Moreover, for any
algebra Lagrange's theorem is not true in general. Moreover, for any 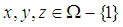 where
where 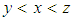 we consider that
we consider that 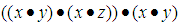
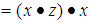
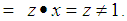 Therefore
Therefore 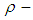 algebra need not be
algebra need not be 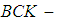 algebra. Further, for any
algebra. Further, for any 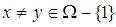 and
and 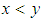 , we consider that
, we consider that 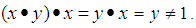 Hence
Hence 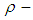 algebra need not be
algebra need not be 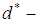 algebra. Also,
algebra. Also, 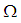 is not edge, if
is not edge, if 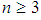 . Since for any
. Since for any 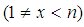 we consider that
we consider that 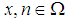 and
and 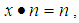 but neither
but neither 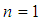 nor
nor 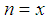 . Moreover,
. Moreover, 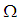 is edge, if
is edge, if 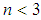 . Since
. Since 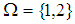 and hence for any
and hence for any 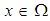 we have
we have 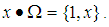 Definition 3.11: Let
Definition 3.11: Let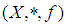 be a
be a 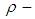 algebra and
algebra and 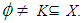 Then K is called a
Then K is called a 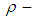 ideal of
ideal of 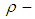 algebra
algebra 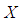 if (1).
if (1). 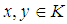 imply
imply 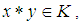 (2).
(2). 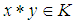 and
and 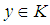 imply
imply 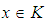 , for all
, for all 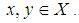 Example 3.12: It is clear,
Example 3.12: It is clear, 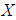 and
and 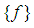 are
are 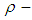 ideal for any
ideal for any 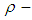 algebra X. Moreover, if
algebra X. Moreover, if 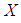 is a
is a 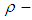 algebra. Then every
algebra. Then every 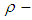 ideal of
ideal of 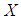 is a
is a 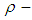 algebra with the same binary operation on
algebra with the same binary operation on 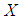 and the constant
and the constant 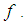 Remark 3.13: By condition (1) in definition 3.11, we consider that every
Remark 3.13: By condition (1) in definition 3.11, we consider that every 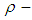 ideal is
ideal is 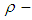 subalgebra and hence
subalgebra and hence 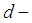 subalgebra.Theorem 3.14: In
subalgebra.Theorem 3.14: In 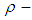 algebra
algebra 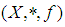 every
every 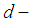 ideal is
ideal is 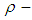 ideal.Proof: Suppose that
ideal.Proof: Suppose that 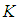 is a
is a 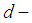 ideal in
ideal in 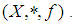 Now, we need to prove that:(1).
Now, we need to prove that:(1). 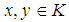 imply
imply 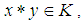 (2).
(2). 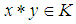 and
and 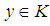 imply
imply 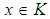 , for all
, for all 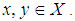 Since
Since 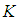 is a
is a 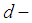 ideal, then condition (2) is hold. Moreover, for any
ideal, then condition (2) is hold. Moreover, for any 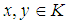 we have
we have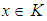 and
and 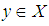 (since
(since 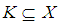 ). This implies that
). This implies that 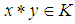 (by condition (2) in definition 2.25). Also, since
(by condition (2) in definition 2.25). Also, since 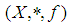 is
is 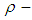 algebra then we have
algebra then we have 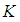 is
is 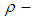 ideal. Remark 3.15: In
ideal. Remark 3.15: In 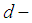 algebra above theory is not true in general.Example 3.16: Let
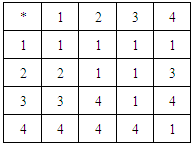
algebra above theory is not true in general.Example 3.16: Let 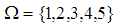 be a
be a 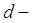 algebra with the following table:
algebra with the following table:
|
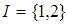 is a
is a 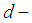 ideal of
ideal of 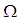 . Further,
. Further, 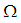 is not
is not 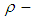 algebra and hence
algebra and hence 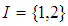 is not
is not 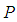 -ideal of
-ideal of 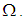 Theorem 3.17: If
Theorem 3.17: If 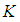 is a
is a 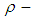 ideal of
ideal of 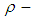 algebra
algebra 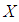 , then
, then 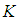 is a
is a 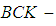 ideal of
ideal of 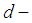 algebra
algebra 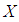 .Proof: Suppose that
.Proof: Suppose that 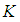 is a
is a 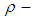 ideal in
ideal in 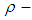 algebra
algebra 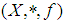 . Then
. Then 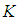 is non-empty subset of
is non-empty subset of 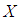 and
and 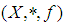 is
is 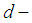 algebra. Thus, we need only to prove that:(1).
algebra. Thus, we need only to prove that:(1). 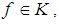 (2).
(2). 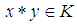 and
and 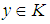 imply
imply 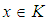 , for all
, for all 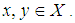 Since
Since 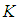 is a
is a 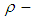 ideal, then condition (2) is hold. Also, there is at least
ideal, then condition (2) is hold. Also, there is at least 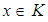 (since
(since 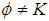 ). This implies that
). This implies that 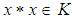 (by condition (1) in definition 3.11), but
(by condition (1) in definition 3.11), but 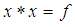 and hence
and hence 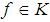 . Then
. Then 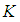 is a
is a 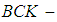 ideal of
ideal of 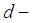 algebra .Definition 3.18: Let
algebra .Definition 3.18: Let 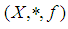 be a
be a 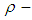 algebra and
algebra and 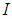 be a subset of
be a subset of 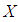 . Then
. Then 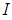 is called
is called 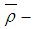 ideal of
ideal of 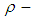 algebra
algebra 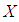 if (1).
if (1). 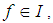 (2).
(2). 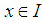 and
and 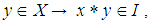 for all
for all 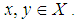 Example 3.19: Let
Example 3.19: Let 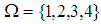 be a
be a 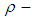 algebra with the following table:
algebra with the following table:
|
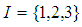 is
is 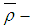 ideal of
ideal of 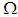 . Further,
. Further, 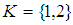 is not
is not 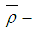 ideal of
ideal of 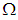 , since
, since 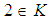 and
and 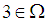 , but
, but 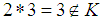 Remark 3.20 It is easy to show that every
Remark 3.20 It is easy to show that every 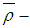 ideal is
ideal is 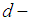 subalgebra. However, the converse is not true and the following example showing that Example 3.21: Let
subalgebra. However, the converse is not true and the following example showing that Example 3.21: Let 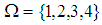 be a
be a 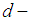 algebra with the following table:
algebra with the following table:
|
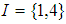 is
is 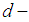 subalgebra of
subalgebra of 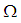 . However,
. However, 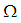 is not
is not 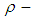 algebra and hence
algebra and hence 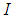 is not
is not 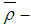 ideal of
ideal of 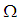 .Remark 3.22: By the above results we have the following diagram:
.Remark 3.22: By the above results we have the following diagram: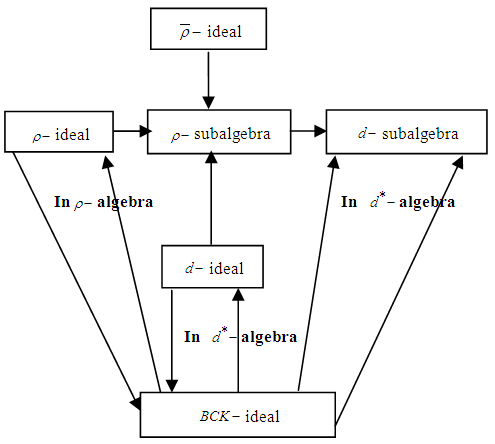 | Figure 1. Diagram showing relationships among some types of algebras |
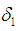 and
and 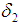 be two permutations in symmetric group
be two permutations in symmetric group 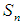 . Then
. Then 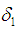 and
and 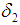 are two permutation maps from
are two permutation maps from 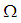 onto
onto 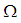 . Further,
. Further, 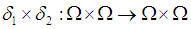 is a product map of permutation maps where
is a product map of permutation maps where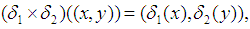
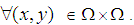 In another side, the map
In another side, the map 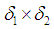 is a permutation in
is a permutation in  as this form
as this form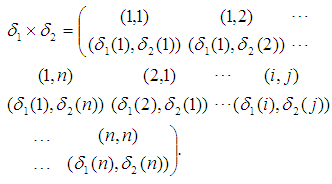 Now, let
Now, let 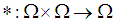 be a binary operation on
be a binary operation on 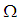 and
and 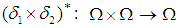 be a map defined by
be a map defined by 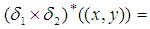
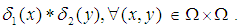 Then the permutation map
Then the permutation map 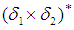 from permutation space
from permutation space 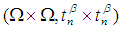 into (
into (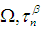 ) for any permutation
) for any permutation 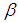 in symmetric group
in symmetric group 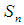 is called multiplication permutation map. Further, it is called multiplication permutation continuous iff the inverse image under
is called multiplication permutation map. Further, it is called multiplication permutation continuous iff the inverse image under 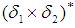 of any open
of any open 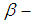 set in
set in 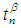 is an open
is an open 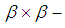 set in
set in 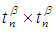 (i.e
(i.e 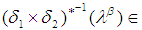
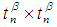 whenever
whenever 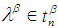 ).Example: 3.24 Suppose that
).Example: 3.24 Suppose that 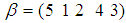 and
and 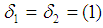 are permutations in symmetric group
are permutations in symmetric group 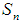 with
with 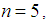 and let
and let 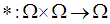 be a binary operation on
be a binary operation on 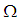 where
where 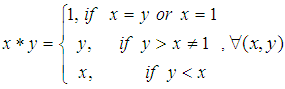
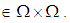 We consider that the multiplication permutation map
We consider that the multiplication permutation map 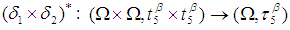 , where
, where 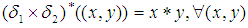
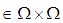 is a multiplication permutation continuous map.Definition 3.25 For any permutation
is a multiplication permutation continuous map.Definition 3.25 For any permutation 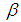 in symmetric group
in symmetric group 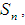 let
let 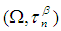 be a permutation topological space and
be a permutation topological space and 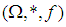 be a
be a 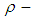 algebra. If
algebra. If 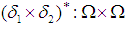
 is a continuous permutation mapping from permutation space
is a continuous permutation mapping from permutation space 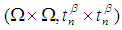 into
into 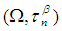 , where
, where 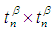 is product topology of
is product topology of 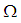 , then we say that
, then we say that 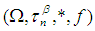 is a permutation topological
is a permutation topological 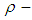 algebra.Example: 3.26 Let
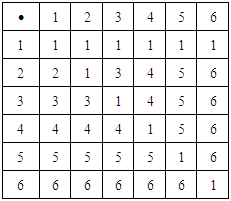
algebra.Example: 3.26 Let 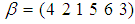 be a permutation in symmetric group
be a permutation in symmetric group 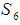 . Then
. Then 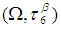 is permutation topological space, where
is permutation topological space, where 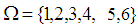 and
and 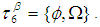 Also, let
Also, let 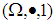 be a
be a 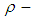 algebra with the following table:
algebra with the following table:
|
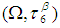 is an indiscrete permutation space. Thus
is an indiscrete permutation space. Thus 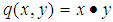 is multiplication permutation continuous map,
is multiplication permutation continuous map, 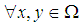 . Then
. Then 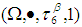 is a permutation topological
is a permutation topological 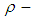 algebra.Remark 3.27: Finally, our new notion (see, Definition 3.25) is given and hence this notion of permutation topological
algebra.Remark 3.27: Finally, our new notion (see, Definition 3.25) is given and hence this notion of permutation topological 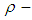 algebra can be considered a special case of topological
algebra can be considered a special case of topological 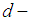 algebra using member in finite group.
algebra using member in finite group.4. Conclusions
- We have initiated a study of
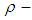 algebras and explained their relations with
algebras and explained their relations with 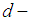 algebras. Moreover, the multiplication permutation map is given and then a permutation topological
algebras. Moreover, the multiplication permutation map is given and then a permutation topological 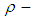 algebra is defined and explained. In future work, we will study the relation between
algebra is defined and explained. In future work, we will study the relation between 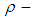 algebras and
algebras and 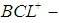 algebras. Moreover, we will investigate some new types of permutation spaces using members in subgroups of symmetric groups instead symmetric groups like Mathieu group
algebras. Moreover, we will investigate some new types of permutation spaces using members in subgroups of symmetric groups instead symmetric groups like Mathieu group 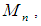 Alternating group
Alternating group 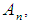 Quaternion group
Quaternion group 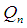 and others. Further, we will consider new constructer in topological algebra is called sub permutation topological
and others. Further, we will consider new constructer in topological algebra is called sub permutation topological 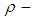 algebra, since each one of these groups on n letters is a subgroup of symmetric group
algebra, since each one of these groups on n letters is a subgroup of symmetric group 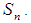
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
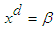 in an Alternating Group for each
in an Alternating Group for each 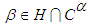 and
and 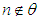 , Journal of the Association of Arab Universities for Basic and Applied Sciences, 10 (1), (2011), 42-50.
, Journal of the Association of Arab Universities for Basic and Applied Sciences, 10 (1), (2011), 42-50.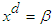 in an Alternating Group for each
in an Alternating Group for each 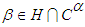 and
and 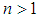 , published in Advances in Linear Algebra & Matrix Theory, 2(2) (2012), 13-19.
, published in Advances in Linear Algebra & Matrix Theory, 2(2) (2012), 13-19.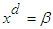 in an Alternating Group for all
in an Alternating Group for all 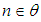 &
&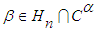 , journal of the Association of Arab Universities for Basic and Applied Sciences, 16, (2014), 38–45.
, journal of the Association of Arab Universities for Basic and Applied Sciences, 16, (2014), 38–45.