Waggas Galib Atshan1, Enaam Hadi Abd2, 3
1Department of Mathematics, College of Computer Science and Mathematics, University of Al-Qadisiya, Diwaniya, Iraq
2Department of Computer, College of Science, University of Kerbala, Kerbala, Iraq
3Department of Mathematics, College of Science, University of Baghdad, Baghdad, Iraq
Correspondence to: Enaam Hadi Abd, Department of Computer, College of Science, University of Kerbala, Kerbala, Iraq.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The object of this paper to study the class 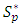 of multivalent functions defined by in the open disk
of multivalent functions defined by in the open disk 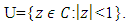 We obtain various results including characterization, coefficients estimates, Subordination Theorems.
We obtain various results including characterization, coefficients estimates, Subordination Theorems.
Keywords:
Analytic function, Multivalent function, Subordination
Cite this paper: Waggas Galib Atshan, Enaam Hadi Abd, Some Properties of Subclass of Multivalent Functions, American Journal of Mathematics and Statistics, Vol. 7 No. 3, 2017, pp. 136-142. doi: 10.5923/j.ajms.20170703.06.
1. Introduction
Let 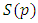 denote the class of functions of the form:
denote the class of functions of the form: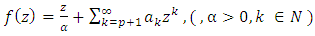 | (1) |
which are analytic and univalent in the open unit disk 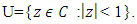 Let
Let  denote the subclass
denote the subclass  of functions of the form:
of functions of the form: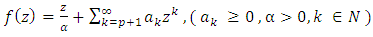 | (2) |
The convolution of two power series 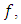 given by(1) and
given by(1) and 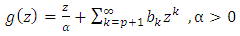 | (3) |
is defined as the following power series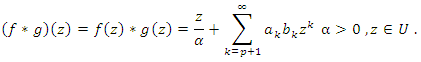 Definition (1): A function
Definition (1): A function 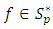 is said to be in the class
is said to be in the class 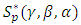 if it satisfies the condition:
if it satisfies the condition: 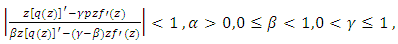 | (4) |
where 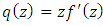
2. Coefficient Estimates
In the following theorem, we obtain the sufficient and necessary condition to be the function 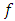 in the class
in the class 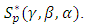 Theorem(2.1): Let the function
Theorem(2.1): Let the function 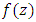 be defined by (2). Then
be defined by (2). Then 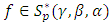 if and only if
if and only if 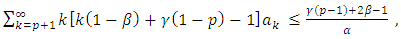 | (5) |
Proof: Suppose that 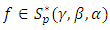 . Then by the condition (4), we have
. Then by the condition (4), we have 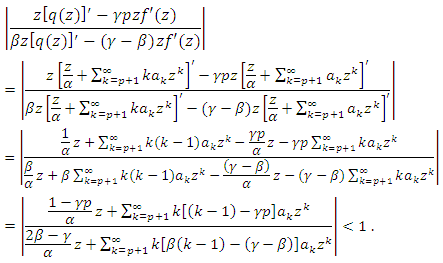 Since
Since 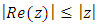 for all z, we have
for all z, we have 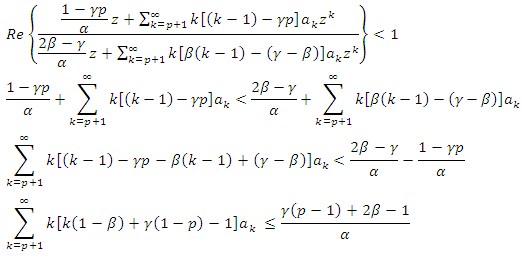 Conversely, assume that the hypothesis(5) and
Conversely, assume that the hypothesis(5) and 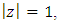 then
then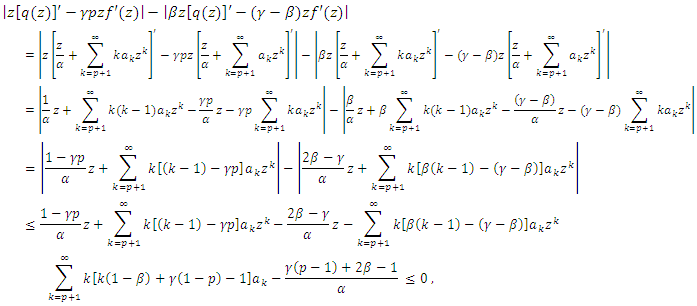 by hypothesis. Then by Maximum modulus theorem, we have
by hypothesis. Then by Maximum modulus theorem, we have 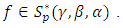 Finally, the result is sharp for the function
Finally, the result is sharp for the function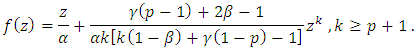 Corollary (2.1): Let the function
Corollary (2.1): Let the function 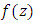 is in the class
is in the class 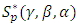 . Then
. Then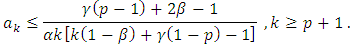
3. Subordination Theorems
Definition(2): Let 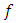 and
and 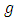 be analytic in the unit disk U. Then
be analytic in the unit disk U. Then 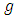 is said to be subordinate to f, written
is said to be subordinate to f, written 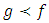 or
or 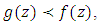 if there exists a Schwarz function
if there exists a Schwarz function 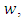 which is analytic in U with
which is analytic in U with 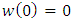 and
and 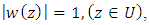 such that
such that 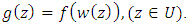 Indeed it is Known that
Indeed it is Known that 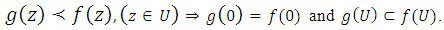 In particular, if the function
In particular, if the function 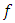 is univalent in U, we have the following equivalence([3], [4]):
is univalent in U, we have the following equivalence([3], [4]):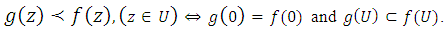 Definition (3) [1]: The fractional derivative of order
Definition (3) [1]: The fractional derivative of order 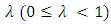 of a function
of a function 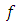 is defined by
is defined by 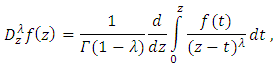 where
where 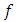 is in Definition(1.1.14), and the multiplicity of
is in Definition(1.1.14), and the multiplicity of 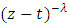 is removed by requiring
is removed by requiring 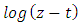 to be real, when
to be real, when 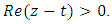 Definition (4): Under the hypothesis of Definition (3), the fractional derivative of order
Definition (4): Under the hypothesis of Definition (3), the fractional derivative of order 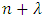 is defined, for a function
is defined, for a function 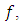 by
by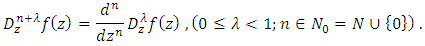 It readily follows from Definition (3) that
It readily follows from Definition (3) that 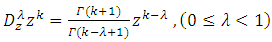 | (6) |
We shall need the concept of Subordination between analytic functions and Subordination theorem of Littlewood [2]. (See also Duren [1])Theorem (3.1): If the function 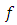 and
and 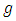 are analytic in U with
are analytic in U with 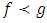 Definition (2), then
Definition (2), then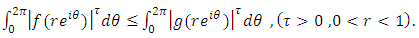 | (7) |
Theorem (3.2): Let 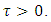 If
If 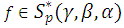 and supposed that
and supposed that 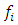 is defined by
is defined by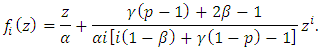 If there exists an analytic function w defined by
If there exists an analytic function w defined by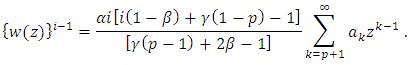 Then, for
Then, for 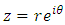 and
and 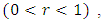
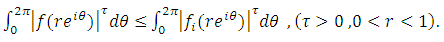 | (8) |
Proof: Let 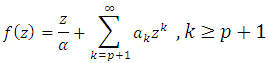 and
and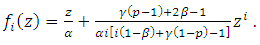 | (9) |
Then, we must show that 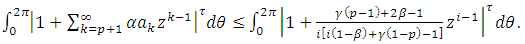 | (10) |
By Theorem (3.1), it suffices to show that 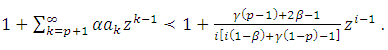 | (11) |
Set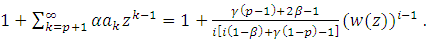 | (12) |
From (12) and (5), we obtain 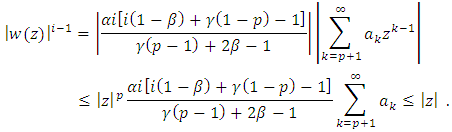 Next, the proof for the first derivative.Theorem (3.3): Let
Next, the proof for the first derivative.Theorem (3.3): Let 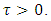 If
If 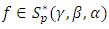 and
and 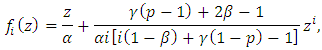 Then for
Then for 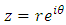 and
and 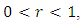
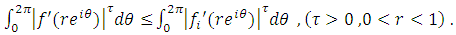 | (13) |
Proof: It is suffices to show that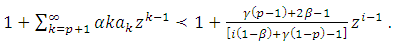 | (14) |
This follows because 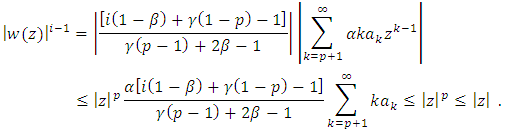 Theorem (3.4): Let
Theorem (3.4): Let 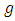 be of the form (3) and
be of the form (3) and 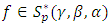 be of the form (2) and let for some
be of the form (2) and let for some 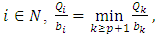 where
where 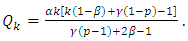 Also, let for such
Also, let for such 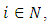 the functions
the functions 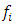 and
and 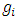 be defined respectively by
be defined respectively by 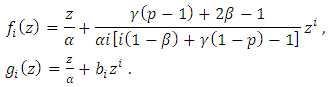 | (15) |
Then, for 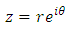 and
and 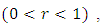
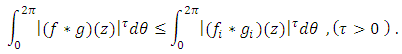 Proof: Convolution of
Proof: Convolution of 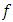 and
and 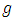 is defined as:
is defined as: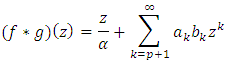 Similarly, from (15), we obtain
Similarly, from (15), we obtain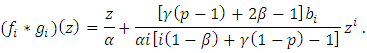 To prove the theorem, we must show that for
To prove the theorem, we must show that for 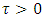 and
and 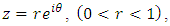
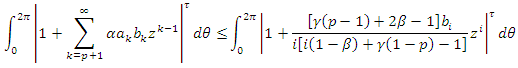 Thus, by applying Theorem (3.1), it would suffice to show that
Thus, by applying Theorem (3.1), it would suffice to show that 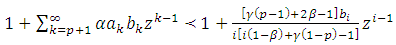 | (16) |
If the subordination (16) holds true, then there exist an analytic function w with 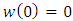 and
and 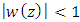 such that
such that 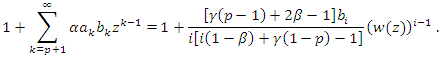 From the hypothesis of the theorem (3.2), there exists an analytic function
From the hypothesis of the theorem (3.2), there exists an analytic function 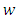 given by
given by 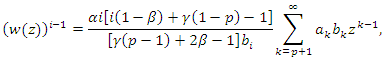 which readily yields
which readily yields 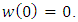 Thus for such function
Thus for such function 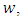 using the hypothesis in the coefficient in equality for the class
using the hypothesis in the coefficient in equality for the class 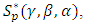 we get
we get 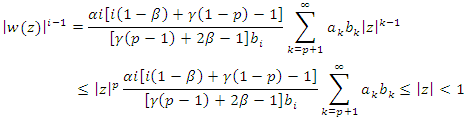 Therefore, the subordination (16) holds true.Now, we discuss the integral means inequalities for
Therefore, the subordination (16) holds true.Now, we discuss the integral means inequalities for 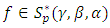 and h defined by
and h defined by 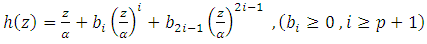 | (17) |
Theorem(3.5): Let 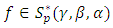 and
and 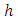 given by (17). If f satisfies
given by (17). If f satisfies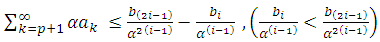 | (18) |
and there exists an analytic function 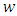 such that
such that 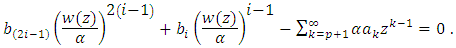 Then, for
Then, for 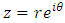 and
and 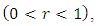
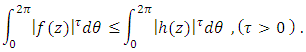 Proof: By putting
Proof: By putting 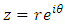 and
and 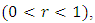 we see that
we see that 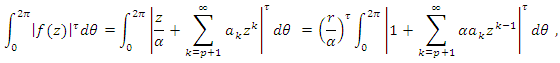 and
and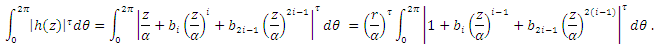 Applying Theorem (3.1), we have to show that
Applying Theorem (3.1), we have to show that 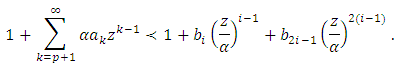 Let us define the function
Let us define the function 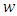 by
by 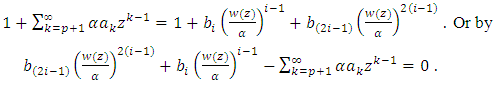 | (19) |
Since for 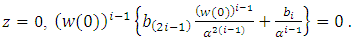 There exists an analytic function w in U such that
There exists an analytic function w in U such that 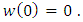 Next, we prove the analytic function w satisfies
Next, we prove the analytic function w satisfies 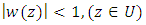 for the condition (18). By (19), we know that,
for the condition (18). By (19), we know that,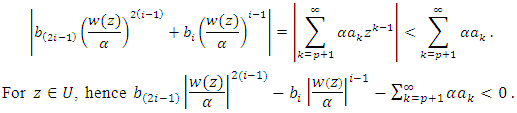 | (20) |
Letting 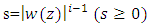 in (20), we define the function
in (20), we define the function 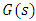 by
by 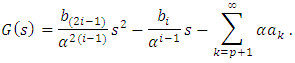 If
If 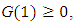 then we have
then we have 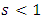 for
for 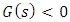 . Indeed we have
. Indeed we have 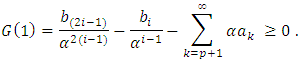 That is
That is 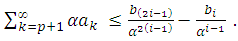 Theorem (3.6): Let
Theorem (3.6): Let 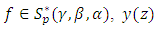 be given by
be given by 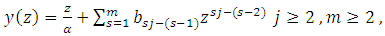 | (21) |
and suppose that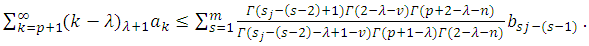 | (22) |
For 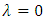 or
or 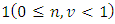 and
and 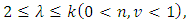 where
where 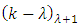 denotes the pochhammer symbol defined by
denotes the pochhammer symbol defined by 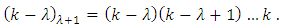 Then for
Then for 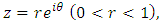
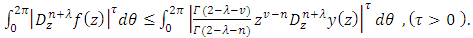 | (23) |
Proof: By means of the fractional derivative formula (6) and Definition (4), we find from (2) that 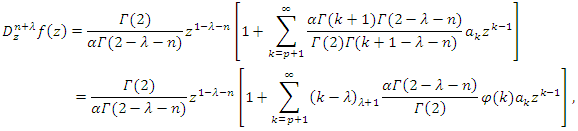 where
where 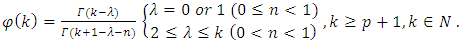 Since
Since 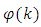 is adecreasing function of
is adecreasing function of 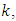 we have
we have 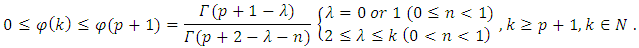 Similarly, by using (21), (6) and Definition (4), we obtain
Similarly, by using (21), (6) and Definition (4), we obtain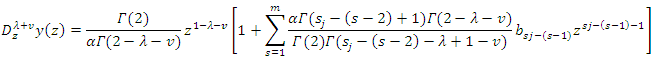 Thus, we have
Thus, we have 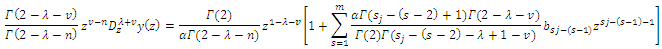 For
For 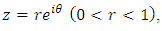 we must show that
we must show that 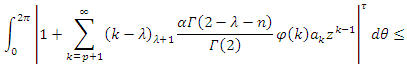
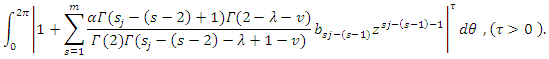 By applying Theorem (2.1). It suffices to show that
By applying Theorem (2.1). It suffices to show that 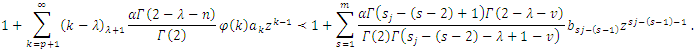 By setting
By setting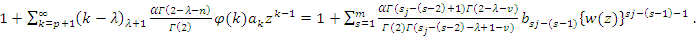 We find that
We find that 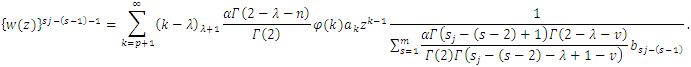 Which readily yields
Which readily yields 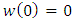 . Therefore, we have
. Therefore, we have 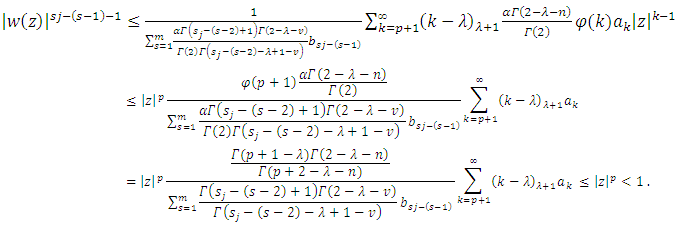 By means of the hypothesis (22) of theorem (3.6).Theorem (3.7): If
By means of the hypothesis (22) of theorem (3.6).Theorem (3.7): If 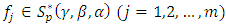 and
and 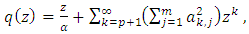 | (24) |
Then 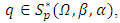 where
where 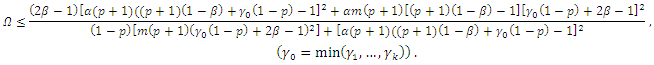 | (25) |
The result is sharp for the functions 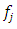 which is given by
which is given by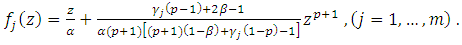 | (26) |
Proof: Since Theorem (2.1) gives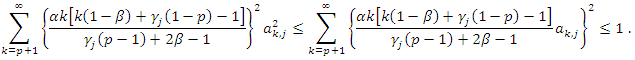 For
For 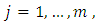 we have
we have 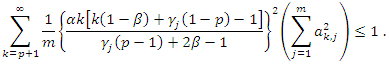 Note that, we have to find the largest
Note that, we have to find the largest 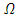 such that
such that 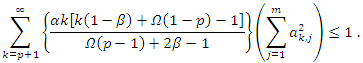 The above inequality is true if
The above inequality is true if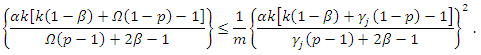 From the previous inequality, we obtain
From the previous inequality, we obtain 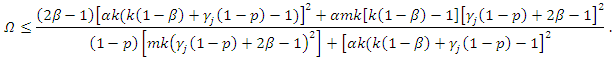 That is,
That is,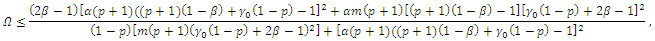
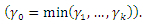
References
| [1] | P. T. Duren, Univalent Function, Grundeheren der Mathematishen wissenchaften 259, Springer-Verlag, New York, Berlin, Heidelberg, Tokyo, (1983). |
| [2] | J. E. Littlewood, On inequalities in the theory of functions, Proc., London Math. Soc., 23(1925), 481-519. |
| [3] | S. S. Miller and P. T. Mocanu , Differential subordinations and univalent functions, Michigan Math. J., 28(1981), 157-171. |
| [4] | S. S. Miller and P. T. Mocanu, Differential subordinations: Theorey and Applications, Series on Monographs and Text Books in Pure and Applied Mathematics Vol. 225, Marcel Dekker, New York and Basel, 2000. |


 of multivalent functions defined by in the open disk
of multivalent functions defined by in the open disk 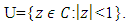 We obtain various results including characterization, coefficients estimates, Subordination Theorems.
We obtain various results including characterization, coefficients estimates, Subordination Theorems.
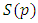 denote the class of functions of the form:
denote the class of functions of the form: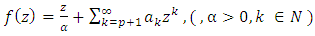
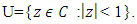 Let
Let 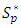 denote the subclass
denote the subclass 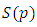 of functions of the form:
of functions of the form: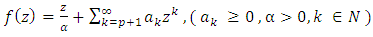
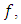 given by(1) and
given by(1) and 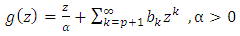
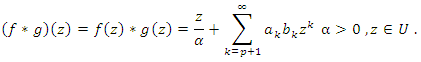 Definition (1): A function
Definition (1): A function 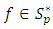 is said to be in the class
is said to be in the class 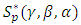 if it satisfies the condition:
if it satisfies the condition: 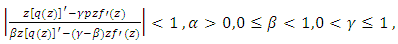
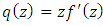
 in the class
in the class  Theorem(2.1): Let the function
Theorem(2.1): Let the function 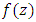 be defined by (2). Then
be defined by (2). Then 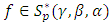 if and only if
if and only if 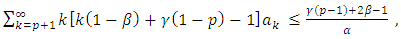
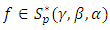 . Then by the condition (4), we have
. Then by the condition (4), we have 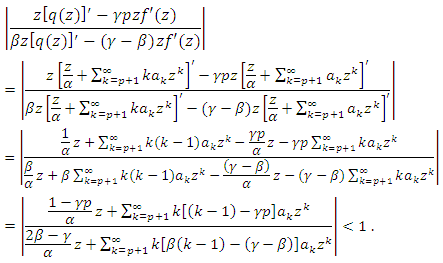 Since
Since 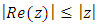 for all z, we have
for all z, we have 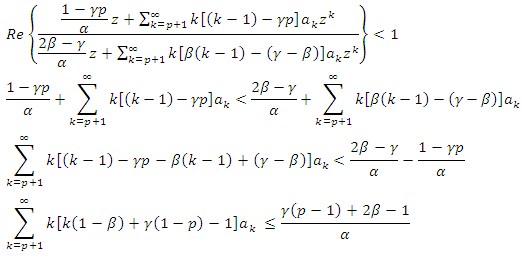 Conversely, assume that the hypothesis(5) and
Conversely, assume that the hypothesis(5) and 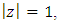 then
then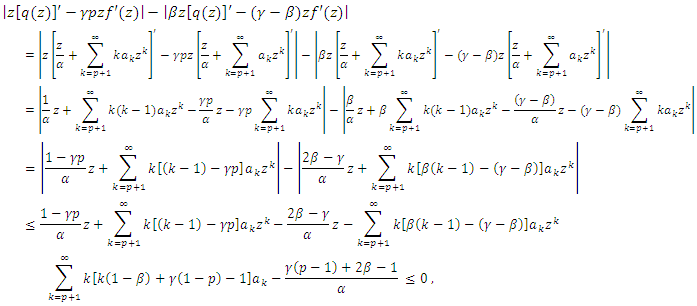 by hypothesis. Then by Maximum modulus theorem, we have
by hypothesis. Then by Maximum modulus theorem, we have 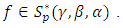 Finally, the result is sharp for the function
Finally, the result is sharp for the function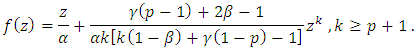 Corollary (2.1): Let the function
Corollary (2.1): Let the function 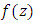 is in the class
is in the class 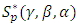 . Then
. Then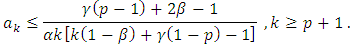
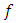 and
and 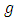 be analytic in the unit disk U. Then
be analytic in the unit disk U. Then 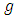 is said to be subordinate to f, written
is said to be subordinate to f, written 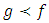 or
or 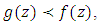 if there exists a Schwarz function
if there exists a Schwarz function 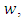 which is analytic in U with
which is analytic in U with 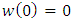 and
and 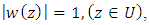 such that
such that 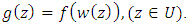 Indeed it is Known that
Indeed it is Known that 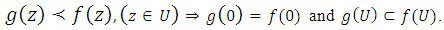 In particular, if the function
In particular, if the function 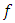 is univalent in U, we have the following equivalence([3], [4]):
is univalent in U, we have the following equivalence([3], [4]):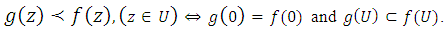 Definition (3) [1]: The fractional derivative of order
Definition (3) [1]: The fractional derivative of order 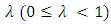 of a function
of a function 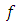 is defined by
is defined by 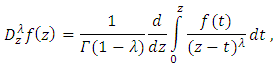 where
where 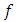 is in Definition(1.1.14), and the multiplicity of
is in Definition(1.1.14), and the multiplicity of 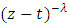 is removed by requiring
is removed by requiring 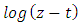 to be real, when
to be real, when 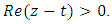 Definition (4): Under the hypothesis of Definition (3), the fractional derivative of order
Definition (4): Under the hypothesis of Definition (3), the fractional derivative of order 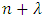 is defined, for a function
is defined, for a function 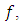 by
by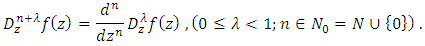 It readily follows from Definition (3) that
It readily follows from Definition (3) that 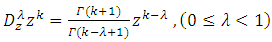
 and
and  are analytic in U with
are analytic in U with  Definition (2), then
Definition (2), then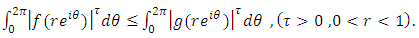
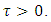 If
If 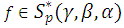 and supposed that
and supposed that 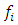 is defined by
is defined by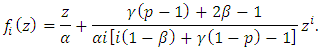 If there exists an analytic function w defined by
If there exists an analytic function w defined by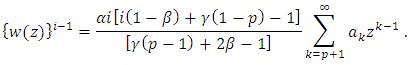 Then, for
Then, for  and
and 
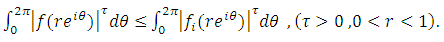
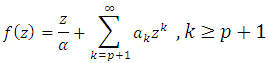 and
and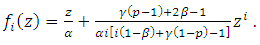
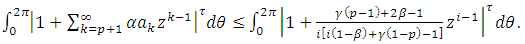
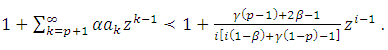
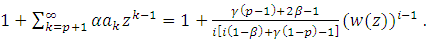
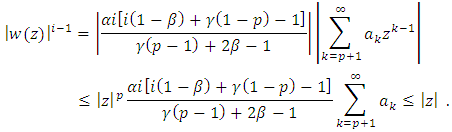 Next, the proof for the first derivative.Theorem (3.3): Let
Next, the proof for the first derivative.Theorem (3.3): Let  If
If 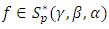 and
and 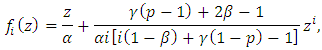 Then for
Then for 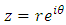 and
and 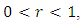
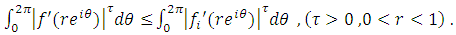
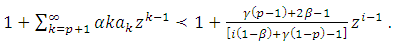
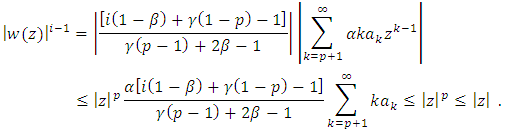 Theorem (3.4): Let
Theorem (3.4): Let  be of the form (3) and
be of the form (3) and 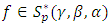 be of the form (2) and let for some
be of the form (2) and let for some 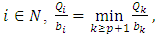 where
where 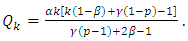 Also, let for such
Also, let for such 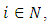 the functions
the functions 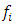 and
and 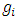 be defined respectively by
be defined respectively by 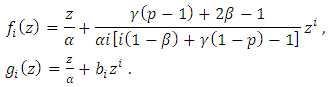
 and
and 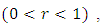
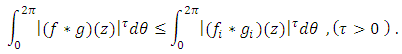 Proof: Convolution of
Proof: Convolution of 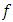 and
and 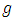 is defined as:
is defined as: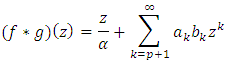 Similarly, from (15), we obtain
Similarly, from (15), we obtain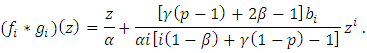 To prove the theorem, we must show that for
To prove the theorem, we must show that for 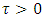 and
and 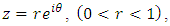
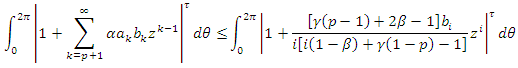 Thus, by applying Theorem (3.1), it would suffice to show that
Thus, by applying Theorem (3.1), it would suffice to show that 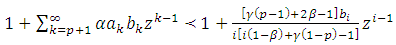
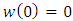 and
and 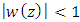 such that
such that 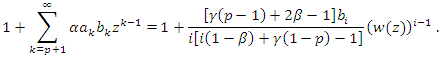 From the hypothesis of the theorem (3.2), there exists an analytic function
From the hypothesis of the theorem (3.2), there exists an analytic function 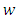 given by
given by 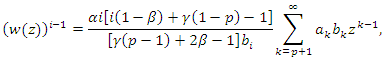 which readily yields
which readily yields 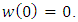 Thus for such function
Thus for such function 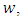 using the hypothesis in the coefficient in equality for the class
using the hypothesis in the coefficient in equality for the class 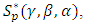 we get
we get 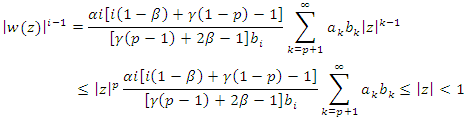 Therefore, the subordination (16) holds true.Now, we discuss the integral means inequalities for
Therefore, the subordination (16) holds true.Now, we discuss the integral means inequalities for 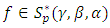 and h defined by
and h defined by 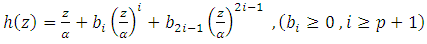
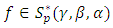 and
and 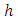 given by (17). If f satisfies
given by (17). If f satisfies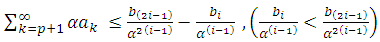
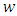 such that
such that 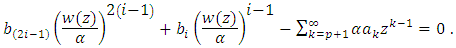 Then, for
Then, for 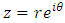 and
and 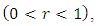
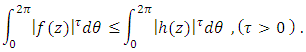 Proof: By putting
Proof: By putting 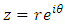 and
and 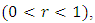 we see that
we see that 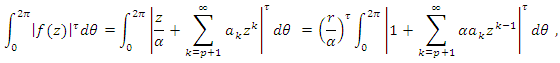 and
and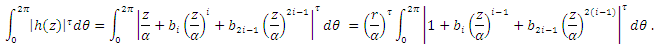 Applying Theorem (3.1), we have to show that
Applying Theorem (3.1), we have to show that 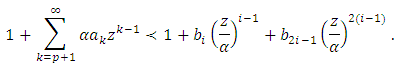 Let us define the function
Let us define the function 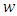 by
by 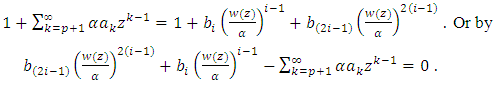
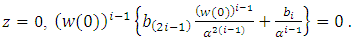 There exists an analytic function w in U such that
There exists an analytic function w in U such that 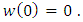 Next, we prove the analytic function w satisfies
Next, we prove the analytic function w satisfies 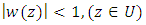 for the condition (18). By (19), we know that,
for the condition (18). By (19), we know that,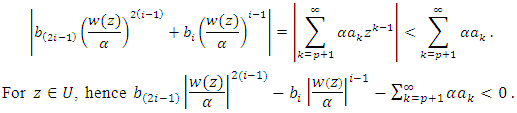
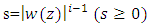 in (20), we define the function
in (20), we define the function 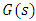 by
by 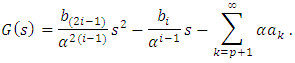 If
If 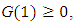 then we have
then we have 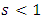 for
for 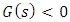 . Indeed we have
. Indeed we have 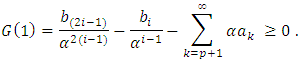 That is
That is 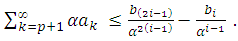 Theorem (3.6): Let
Theorem (3.6): Let 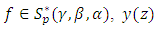 be given by
be given by 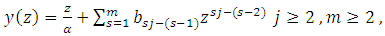
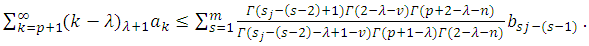
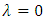 or
or 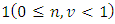 and
and 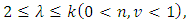 where
where 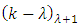 denotes the pochhammer symbol defined by
denotes the pochhammer symbol defined by 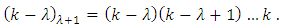 Then for
Then for 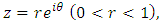
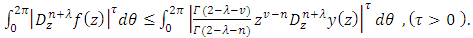
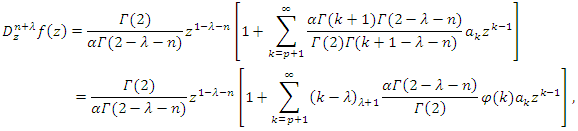 where
where 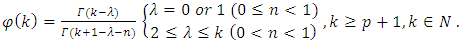 Since
Since 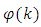 is adecreasing function of
is adecreasing function of 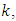 we have
we have 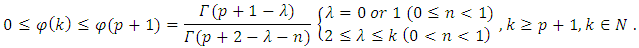 Similarly, by using (21), (6) and Definition (4), we obtain
Similarly, by using (21), (6) and Definition (4), we obtain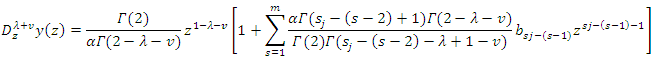 Thus, we have
Thus, we have 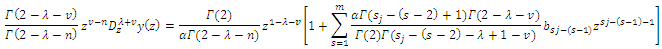 For
For 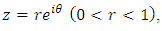 we must show that
we must show that 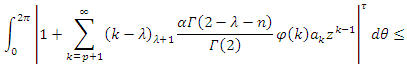
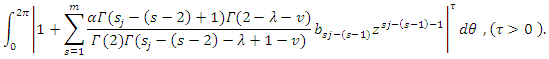 By applying Theorem (2.1). It suffices to show that
By applying Theorem (2.1). It suffices to show that 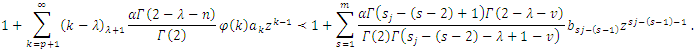 By setting
By setting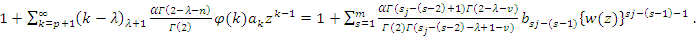 We find that
We find that 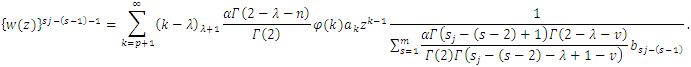 Which readily yields
Which readily yields 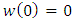 . Therefore, we have
. Therefore, we have 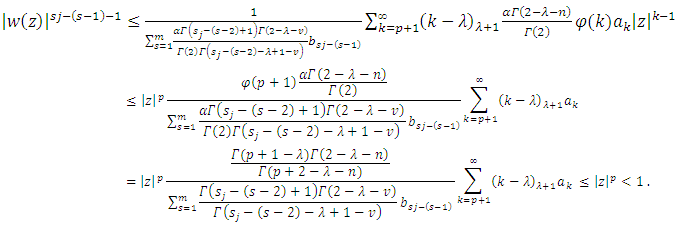 By means of the hypothesis (22) of theorem (3.6).Theorem (3.7): If
By means of the hypothesis (22) of theorem (3.6).Theorem (3.7): If 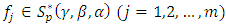 and
and 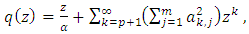
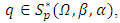 where
where 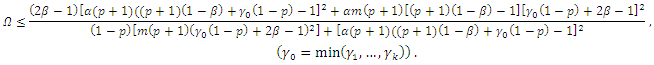
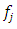 which is given by
which is given by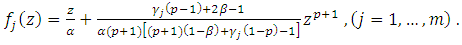
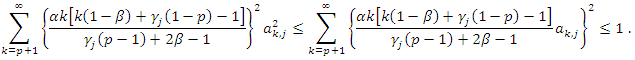 For
For 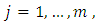 we have
we have 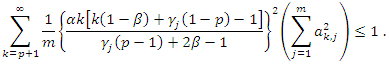 Note that, we have to find the largest
Note that, we have to find the largest  such that
such that 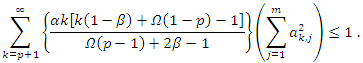 The above inequality is true if
The above inequality is true if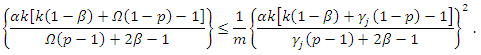 From the previous inequality, we obtain
From the previous inequality, we obtain 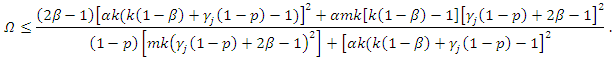 That is,
That is,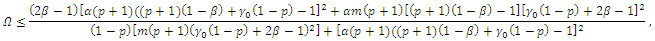
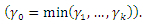
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML