-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2017; 7(3): 113-124
doi:10.5923/j.ajms.20170703.04

Generalization and Proof of the Littlewood Conjecture
Kaveh Mozafari
ExcellenSation Inc., Toronto, Ontario, Canada
Correspondence to: Kaveh Mozafari, ExcellenSation Inc., Toronto, Ontario, Canada.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The aim of this paper is to provide proof of the Littlewood conjecture (theorem). The Littlewood conjecture proposed by John Edensor Littlewood close to 90 years ago. There are numerous applications of the conjecture to this day; however, a complete proof over real number is yet to be provided. The conjecture proposes that the limit inferior (roughly speaking the lower bound of limit) of multiplication between an infinitely large number, n, and the distances between two real numbers each multiplied by n, from their closest integer approaches zero. This paper provides a proof of the Littlewood conjecture. The proof segregates the real numbers in two forms of rational and irrational numbers. All parts of the proof utilize the analytical approach of limit. Initially, a proof of rational numbers is provided. In consequent to such proof, the validity of the conjecture is revealed by the Archimedean's property of real number followed by squeeze theorems for all real numbers. After such claim, it would be evident that the Littlewood conjecture is a special form of a bigger limit inferior which approaches zero.
Keywords: Littlewood conjecture proof, Littlewood conjecture generalization, Diophantine approximation
Cite this paper: Kaveh Mozafari, Generalization and Proof of the Littlewood Conjecture, American Journal of Mathematics and Statistics, Vol. 7 No. 3, 2017, pp. 113-124. doi: 10.5923/j.ajms.20170703.04.
1. Introduction
- Littlewood Conjecture is an interesting conjecture in mathematics which was proposed by John Edensor Littlewood close to 90 years ago. The conjecture considered an open problem in mathematics since 2016. The presented paper proves the conjecture while it generalizes it to a theorem which states that limit inferior of multiplication of a finite number of real number's distance from the nearest integer is always zero. By limit inferior, we are referring to the lower bound of the limit upon its existence. For example limit inferior of cosine function for real value would be -1, which can be represented as follow.
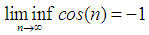 It suffices to say that since the value of the "n" and distance between two points are always non-negative values we can securely assume their multiplications would be at least zero. That is in the subsequent sections of the existing paper we would not investigate if negative values are possible solutions to the Littlewood conjecture.
It suffices to say that since the value of the "n" and distance between two points are always non-negative values we can securely assume their multiplications would be at least zero. That is in the subsequent sections of the existing paper we would not investigate if negative values are possible solutions to the Littlewood conjecture.2. Preliminaries
- Littlewood Conjecture states that
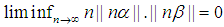 , where ||b|| for
, where ||b|| for 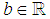 (set of all real numbers) means the distance of b from the closest integer while
(set of all real numbers) means the distance of b from the closest integer while 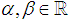 . Moreover
. Moreover 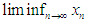 is defined as follow.
is defined as follow.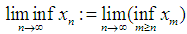 In the present paper the Littlewood conjecture is proven to be correct by first proving the conjecture for rational number and then extending it to all real numbers. At the end the conjecture is extended to cover more terms as follow.
In the present paper the Littlewood conjecture is proven to be correct by first proving the conjecture for rational number and then extending it to all real numbers. At the end the conjecture is extended to cover more terms as follow.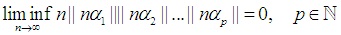 To get limit inferior, we need to realize where the lowest point may occur. It is evident that the function does not result in a negative value since each term is non-negative. Therefore, it is safe to assume the lowest possible value is zero. On the other side, we propose that with the correct choice of n values we always would get zeros from the function in a periodic manner that will be explained in the proceeding sections.
To get limit inferior, we need to realize where the lowest point may occur. It is evident that the function does not result in a negative value since each term is non-negative. Therefore, it is safe to assume the lowest possible value is zero. On the other side, we propose that with the correct choice of n values we always would get zeros from the function in a periodic manner that will be explained in the proceeding sections.3. Proof of Littlewood Conjecture
- Lemma 1.
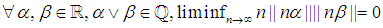 , where for
, where for  , we denote
, we denote  as the distance to the nearest integer.Proof. To provide the proof, we need to separate the proof into four main cases. Without loss of generality assume
as the distance to the nearest integer.Proof. To provide the proof, we need to separate the proof into four main cases. Without loss of generality assume  is rational. Therefore,
is rational. Therefore, 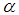 can be write as follow.
can be write as follow.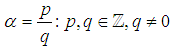 Where
Where 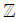 is the set of all integers.Case 1.
is the set of all integers.Case 1. 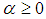 Now we try to write
Now we try to write 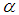 as mixed fraction.
as mixed fraction.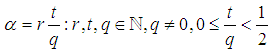 Note in such case the closest integer to
Note in such case the closest integer to 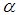 would be r
would be r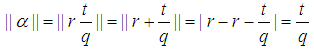 Also Note
Also Note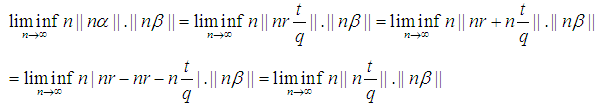 Without loss of generality take:
Without loss of generality take: 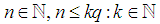
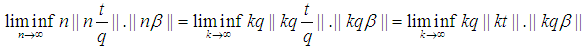 Note
Note 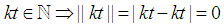 and
and 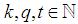 we need to prove for any
we need to prove for any 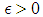 there exist an
there exist an 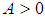 such for all
such for all 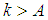 the
the 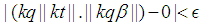 holds. Since
holds. Since 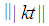 is an integer then
is an integer then 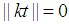 the following can be concluded.
the following can be concluded.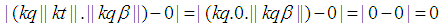 and
and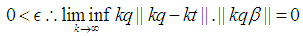 Therefore, for the presented case the proceeding statement is coorect.
Therefore, for the presented case the proceeding statement is coorect.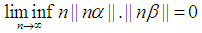 Case 2.
Case 2.  Now we try to write
Now we try to write  in mixed fraction format.
in mixed fraction format.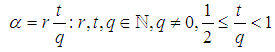 In the presented case, the closest integer to
In the presented case, the closest integer to 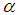 would be r+1
would be r+1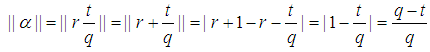 Also Note
Also Note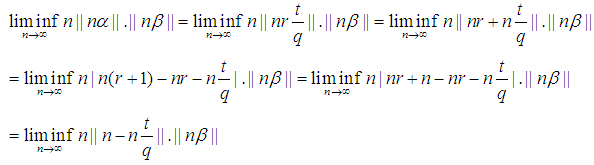 Without loss of generality take:
Without loss of generality take: 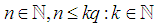
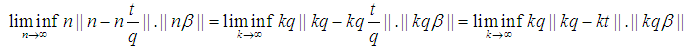 Note
Note 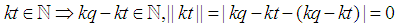 and
and 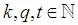 we need to prove for any
we need to prove for any 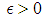 there exist an
there exist an 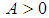 such for all
such for all 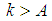 the
the 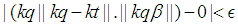 holds. Since
holds. Since 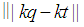 is an integer then
is an integer then 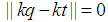 the following can be concluded.
the following can be concluded. and
and 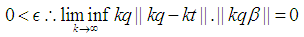 Therefore, for the presented case the proceeding statement is coorect.
Therefore, for the presented case the proceeding statement is coorect.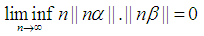 Case 3.
Case 3. 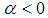 Now we try to write
Now we try to write 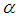 in mixed fraction.
in mixed fraction.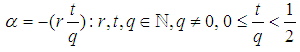 Note in such case the closest integer to
Note in such case the closest integer to 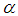 would be -r
would be -r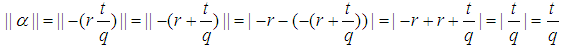 Also Note
Also Note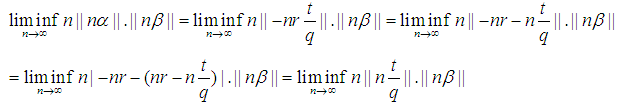 Without loss of generality take:
Without loss of generality take: 
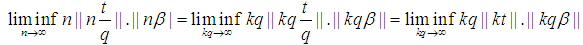 Note
Note 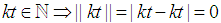 and
and 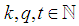 we need to prove for any
we need to prove for any 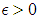 there exist an
there exist an 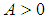 such for all
such for all 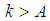 the
the 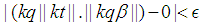 holds. Since
holds. Since 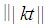 is an integer then
is an integer then 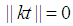 the following can be concluded.
the following can be concluded.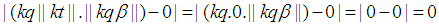 and
and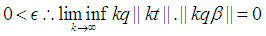 Therefore, for the presented case the proceeding statement is coorect.
Therefore, for the presented case the proceeding statement is coorect.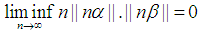 Case 4.
Case 4. 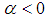 Now we try to write
Now we try to write 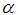 in mixed fraction.
in mixed fraction.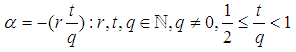 Note in such case the closest integer to
Note in such case the closest integer to 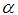 would be -(r+1)
would be -(r+1)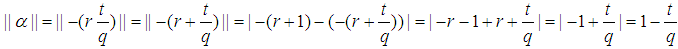 Also Note
Also Note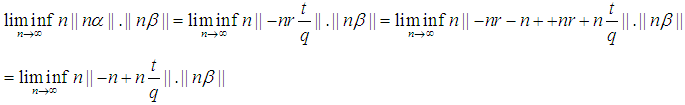 Without loss of generality take:
Without loss of generality take: 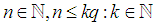
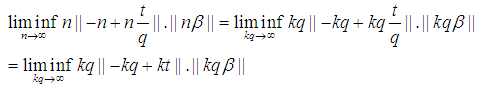 Note
Note 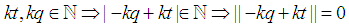 and
and 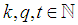 we need to prove for any
we need to prove for any 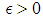 there exist an
there exist an 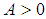 such for all
such for all 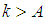 the
the 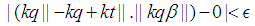 holds. Since is an integer then
holds. Since is an integer then 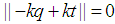 the following can be concluded.
the following can be concluded.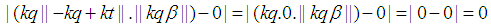 and
and 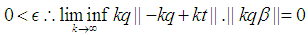 Therefore, for the presented case the proceeding statement is coorect.
Therefore, for the presented case the proceeding statement is coorect.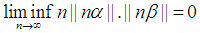 That is, we have shown the Littlewood conjecture holds for all rational number.Corollary 1.1. Given
That is, we have shown the Littlewood conjecture holds for all rational number.Corollary 1.1. Given 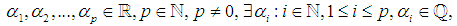 then we can conclude that
then we can conclude that 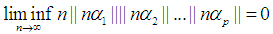 By Lemma 1. we know the
By Lemma 1. we know the 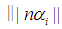 would be equal to zero. We need to prove for any
would be equal to zero. We need to prove for any  there exist an
there exist an 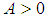 such for all
such for all 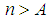 the
the 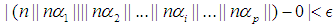 holds. Since
holds. Since 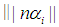 is an integer then
is an integer then 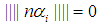 the following can be concluded.
the following can be concluded.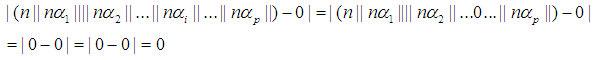 and
and 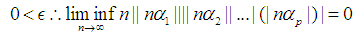 Hence, we can conclude the following for the case that at least one of
Hence, we can conclude the following for the case that at least one of 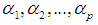 is a rational number.
is a rational number.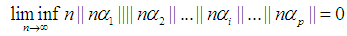 Lemma 2.
Lemma 2. 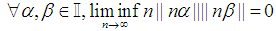 , where for
, where for 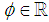 , we denote
, we denote 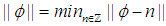 Proof. To provide the proof, we need to the matters into four main cases. Without loss of generality we proceed with proof with focusing on
Proof. To provide the proof, we need to the matters into four main cases. Without loss of generality we proceed with proof with focusing on 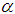 an arbitrary the irrational number
an arbitrary the irrational number 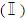 .Case 5.
.Case 5. 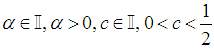 We can express
We can express 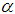 as follow.
as follow.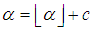 Where
Where 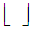 is the floor function.Note:
is the floor function.Note: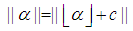 The closest integer to
The closest integer to 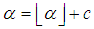 with the given constrains would be
with the given constrains would be 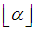
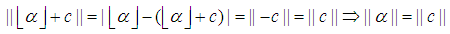
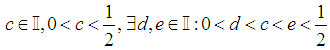 Without loss of generality assume
Without loss of generality assume 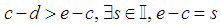 By Archimedes Axiom
By Archimedes Axiom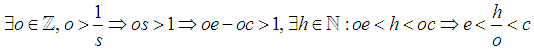 Where
Where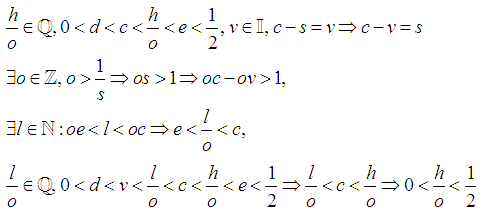 Assign
Assign 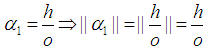 Note
Note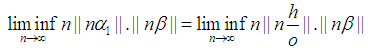 Without loss of generality take:
Without loss of generality take: 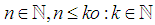
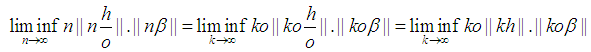 Note
Note 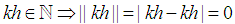 . We need to prove for any
. We need to prove for any 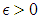 there exist an
there exist an 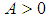 such for all
such for all 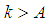 the
the 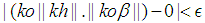 holds. Since
holds. Since 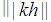 is an integer then
is an integer then 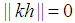 the following can be concluded.
the following can be concluded.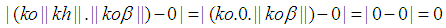 and
and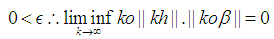 Now take
Now take 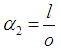
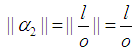 Also Note
Also Note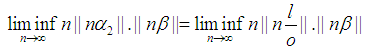 Without loss of generality take:
Without loss of generality take: 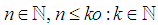
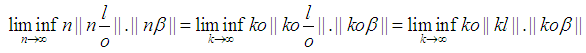 Note
Note 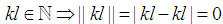 . We need to prove for any
. We need to prove for any 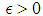 there exist an
there exist an 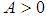 such for all
such for all 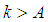 the
the 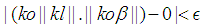 holds. Since
holds. Since 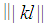 is an integer then
is an integer then 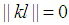 the following can be concluded.
the following can be concluded.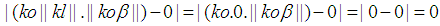 and
and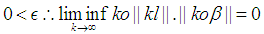 Note
Note 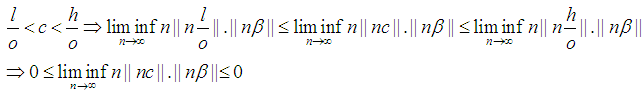 By Squeeze theorem
By Squeeze theorem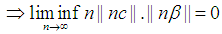 From
From 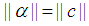
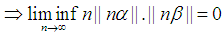 Case 6.
Case 6. 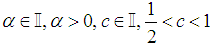 We can express
We can express 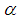 as follow.
as follow.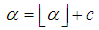 Note
Note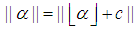 The closest integer to
The closest integer to 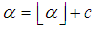 with the given constrains would be
with the given constrains would be 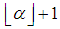
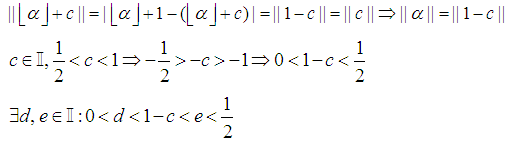 Without loss of generality assume
Without loss of generality assume 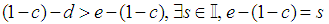 By Archimedes Axiom
By Archimedes Axiom 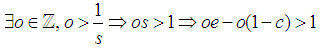
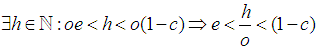 Where
Where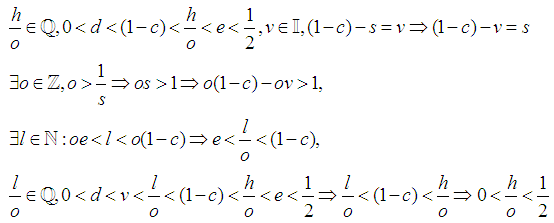 Assign
Assign 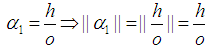 Note
Note 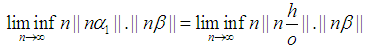 Without loss of generality take:
Without loss of generality take: 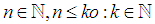
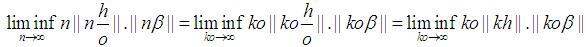 Note
Note 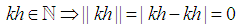 . We need to prove for any
. We need to prove for any 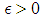 there exist an
there exist an 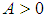 such for all
such for all 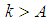 the
the 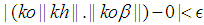 holds. Since
holds. Since 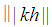 is an integer then
is an integer then 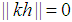 the following can be concluded.
the following can be concluded.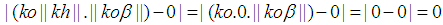 and
and 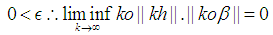 Now take
Now take 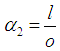
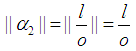 Also Note
Also Note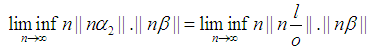 Without loss of generality take:
Without loss of generality take: 
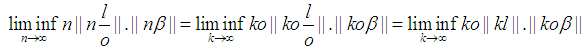 Note
Note 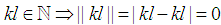 . We need to prove for any
. We need to prove for any 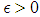 there exist an
there exist an 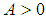 such for all
such for all 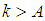 the
the 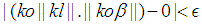 holds. Since
holds. Since 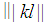 is an integer then
is an integer then 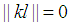 the following can be concluded.
the following can be concluded.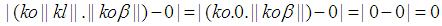 and
and 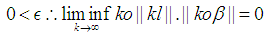 Note:
Note: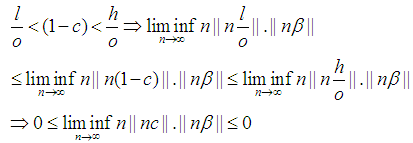 By Squeeze theorem
By Squeeze theorem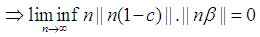 Since
Since 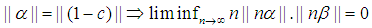 Case 7.
Case 7. 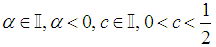 We can express
We can express 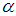 as follow.
as follow.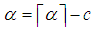 Where
Where 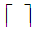 is the floor function.Note:
is the floor function.Note: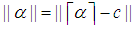 The closest integer to
The closest integer to 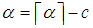 with the given constrains would be
with the given constrains would be 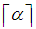
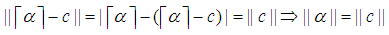
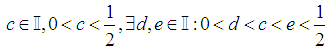 Without loss of generality take
Without loss of generality take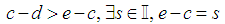 By Archimedes Axiom
By Archimedes Axiom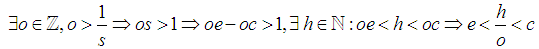 Where
Where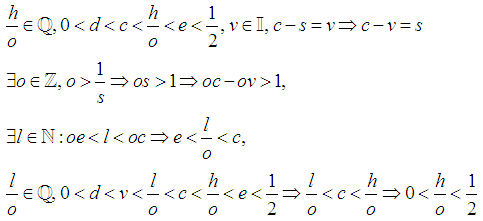 Assign
Assign 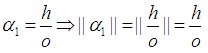 Note
Note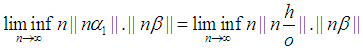 Without loss of generality take:
Without loss of generality take: 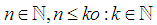
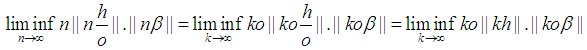 Note
Note 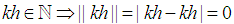 . We need to prove for any
. We need to prove for any  there exist an
there exist an 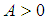 such for all
such for all 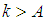 the
the 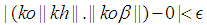 holds. Since
holds. Since 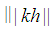 is an integer then
is an integer then 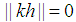 the following can be concluded.
the following can be concluded.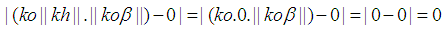 and
and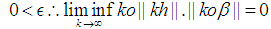 Take
Take 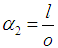
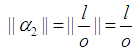 Also Note
Also Note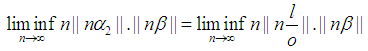 Without loss of generality take:
Without loss of generality take: 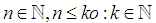
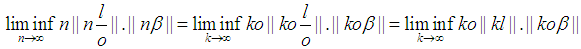 Note
Note 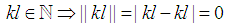 . We need to prove for any
. We need to prove for any 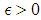 there exist an
there exist an 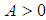 such for all
such for all 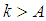 the
the 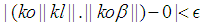 holds. Since
holds. Since 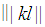 is an integer then
is an integer then 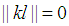 the following can be concluded.
the following can be concluded.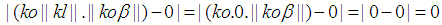 and
and 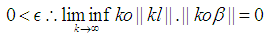 Note:
Note: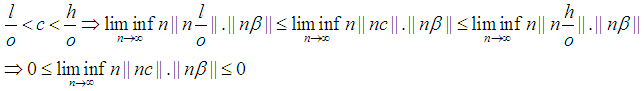 By Squeeze theorem
By Squeeze theorem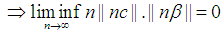 From
From 
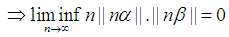 Case 8.
Case 8. 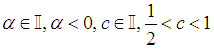 We can express
We can express 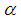 as follow.
as follow.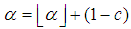 Note
Note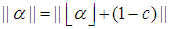 The closest integer to
The closest integer to 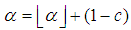 with the given constrains would be
with the given constrains would be 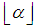
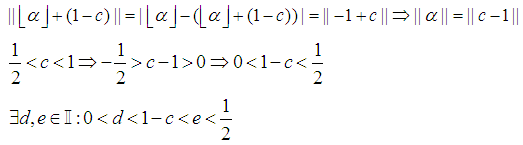 Without loss of generality
Without loss of generality 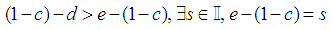 By Archimedes Axiom
By Archimedes Axiom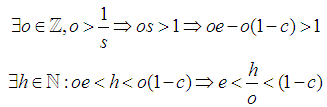 Where
Where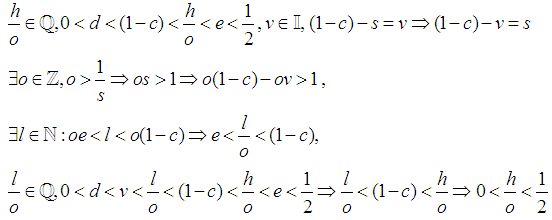 Assign
Assign 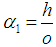
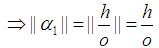 Note
Note 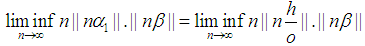 Without loss of generality
Without loss of generality 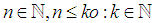
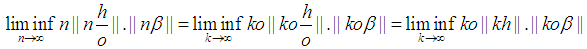 Note
Note 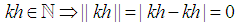 . We need to prove for any
. We need to prove for any 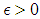 there exist an
there exist an 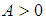 such for all
such for all 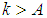 the
the 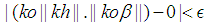 holds. Since
holds. Since 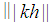 is an integer then
is an integer then 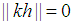 the following can be concluded.
the following can be concluded.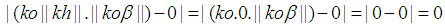 and
and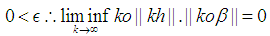 Now take
Now take 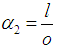
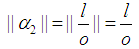 Also Note
Also Note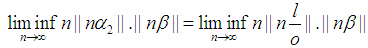 Without loss of generality take:
Without loss of generality take: 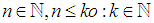
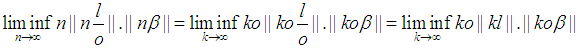 Note
Note 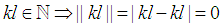 . We need to prove for any
. We need to prove for any  there exist an
there exist an 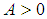 such for all
such for all 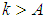 the
the 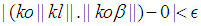 holds. Since
holds. Since 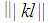 is an integer then
is an integer then 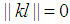 the following can be concluded.
the following can be concluded.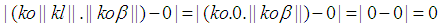 and
and 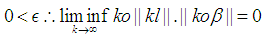 Note:
Note: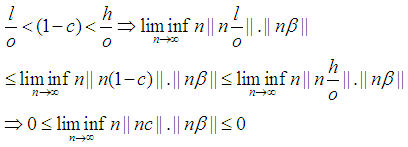 By Squeeze theorem
By Squeeze theorem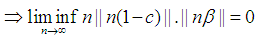 Since
Since 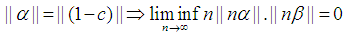 In all cases we have concluded the following.
In all cases we have concluded the following.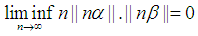 Therefore we can say the Little Conjecture holds for all real numbers.Corollary 2.1. Given
Therefore we can say the Little Conjecture holds for all real numbers.Corollary 2.1. Given 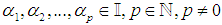 , Then we can conclude that
, Then we can conclude that 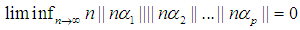 Without loss of generality, by Lemma 2 we have the following.
Without loss of generality, by Lemma 2 we have the following.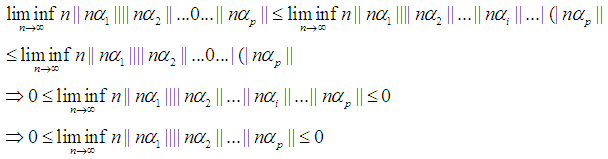 By Squeeze theorem
By Squeeze theorem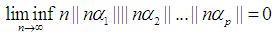
4. Generalization
- It suffices to focus on the generalized form of Littlewood conjecture based on the provided proof. Consequently, the following theorem is expectedly obtained.Theorem 3.
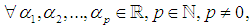
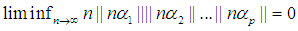 , where for
, where for 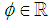 , we denote
, we denote 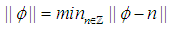 Proof. To prove the theorem we refer to the Corollary 1.1. and Corollary 2.1. which are resulted from Lemma 1. and Lemma 2. respectively. The two corollary contain all possibilities of
Proof. To prove the theorem we refer to the Corollary 1.1. and Corollary 2.1. which are resulted from Lemma 1. and Lemma 2. respectively. The two corollary contain all possibilities of 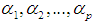 over the real numbers. Therefore we can conclude.
over the real numbers. Therefore we can conclude.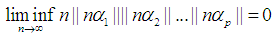 The possible applications of the theorem are beyond the scope of the presented paper, and hopefully, subsequent papers would cover portions of such claim.
The possible applications of the theorem are beyond the scope of the presented paper, and hopefully, subsequent papers would cover portions of such claim. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML