-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2017; 7(3): 108-112
doi:10.5923/j.ajms.20170703.03

Linear Transformation on Strongly Magic Squares
Neeradha. C. K.1, T. S. Sivakumar2, V. Madhukar Mallayya3
1Department of Science & Humanities, Mar Baselios College of Engineering & Technology, Trivandrum, India
2Department of Mathematics, Mar Ivanios College, Trivandrum, India
3Department of Mathematics, Mohandas College of Engineering & Technology, Trivandrum, India
Correspondence to: Neeradha. C. K., Department of Science & Humanities, Mar Baselios College of Engineering & Technology, Trivandrum, India.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A magic square is a square array of numbers where the rows, columns, diagonals and co-diagonals add up to the same number. Several studies on computational aspects of magic squares are being carried out recently revealing patterns, some of which have led to analytic insights, theorems or combinatorial results. Magic squares can be used for solving certain complicated and complex problems connected with the algebra and combinatorial geometry of polyhedra, polytopes. While magic squares are recreational on one hand they can be treated somewhat more seriously in higher mathematics on the other hand. This paper discuss about a well-known class of magic squares; the strongly magic square. The strongly magic square is a magic square with a stronger property that the sum of the entries of the sub-squares taken without any gaps between the rows or columns is also the magic constant. In this paper a generic definition for Strongly Magic Squares is given. The main objective of the paper is to define a function on strongly magic squares which can be established as a group homomorphism and isomorphism. The transition of a set of strongly magic squares to an abelian group can be seen in the paper. The paper deals with the formation of a vector space for the set of all strongly magic squares and particular types of strongly magic squares. The paper also sheds light on linear transformation on Strongly Magic Squares. The kernel of the mapping is also obtained.
Keywords: Magic Square, Strongly Magic Square, Homomorphism, Isomorphism, Linear transformation, Kernel
Cite this paper: Neeradha. C. K., T. S. Sivakumar, V. Madhukar Mallayya, Linear Transformation on Strongly Magic Squares, American Journal of Mathematics and Statistics, Vol. 7 No. 3, 2017, pp. 108-112. doi: 10.5923/j.ajms.20170703.03.
Article Outline
1. Introduction
- Magic squares generally fall into the realm of recreational mathematics (Pasles, 2008), (Pickover, 2002) however a few times in the past century and more recently, they have become the interest of more-serious mathematicians. Magic squares have spelt fascination to mankind throughout history and all across the globe. A normal magic square is a square array of consecutive numbers from 1…n^2 where the rows, columns, diagonals and co-diagonals add up to the same number. The constant sum is called magic constant or magic number. Along with the conditions of normal magic squares, strongly magic square of order 4 have a stronger property that the sum of the entries of the sub-squares taken without any gaps between the rows or columns is also the magic constant. The study on numerical properties of strongly magic squares of order 4 have been carried out by astrologer turned mathematician Padmakumar (Padmakumar, 1995). Another study carried out by Stanley [8] on magic Squares using the tools of Commutative Algebra which makes use of graded rings to define a hilbert series (Qimh Richey Xantcha, 2012). The homomorphic and isomorphic properties on semi magic squares has also studied recently (Sreeranjini, 2014). In this paper some advanced mathematical properties of the strongly magic squares are discussed.
2. Mathematical Preliminaries
2.1. Magic Square
- A magic square of order n over a field
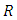 where
where 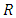 denotes the set of all real numbers is an nth order matrix
denotes the set of all real numbers is an nth order matrix 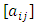 with entries in
with entries in 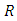 such that adhere to this paper in appearance as closely as possible.
such that adhere to this paper in appearance as closely as possible. 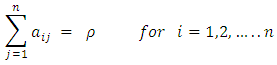 | (1) |
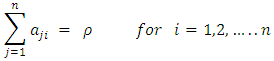 | (2) |
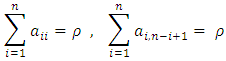 | (3) |
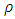 represents the magic constant (Small, 1988).
represents the magic constant (Small, 1988).2.2. Magic Constant
- The constant
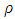 in the above definition is known as the magic constant or magic number. The magic constant of the magic square A is denoted as
in the above definition is known as the magic constant or magic number. The magic constant of the magic square A is denoted as 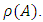 In the example given below the magic constant of A is 15 and B is 34.
In the example given below the magic constant of A is 15 and B is 34.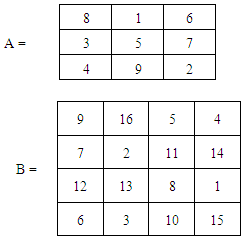
2.3. Strongly Magic Square (SMS): Generic Definition
- A strongly magic square over a field
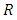 is a matrix
is a matrix 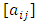 of order
of order 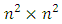 with entries in
with entries in 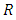 such that
such that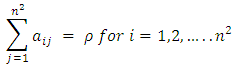 | (4) |
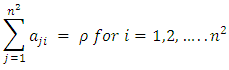 | (5) |
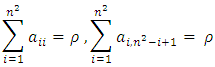 | (6) |
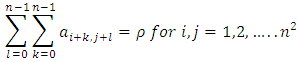 | (7) |
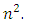 Equation (4) represents the row sum, equation (5) represents the column sum, equation (6) represents the diagonal & co-diagonal sum, equation (7) represents the
Equation (4) represents the row sum, equation (5) represents the column sum, equation (6) represents the diagonal & co-diagonal sum, equation (7) represents the 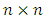 sub-square sum with no gaps in between the elements of rows or columns and is denoted as
sub-square sum with no gaps in between the elements of rows or columns and is denoted as 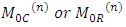 and
and 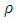 is the magic constant.Note: The
is the magic constant.Note: The 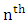 order sub-square sum with k column gaps or k row gaps is generally denoted as
order sub-square sum with k column gaps or k row gaps is generally denoted as 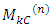 or
or 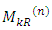 respectively.
respectively.2.4. Group Homomorphism
- A mapping
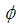 from a group
from a group 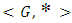 into a group
into a group 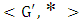 is a homomorphism of
is a homomorphism of 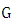 into
into 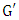 if
if 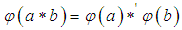 for all
for all 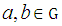 [9]
[9]2.5. Group Isomorphism
- A one to one onto homomorphism
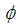 from a group
from a group 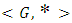 into a group
into a group 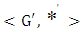 is defined as isomorphism (Fraleigh, 2003).
is defined as isomorphism (Fraleigh, 2003).2.6. A One to One and onto Mapping
- A function
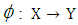 is one to one if
is one to one if 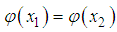 only when
only when 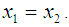 The function
The function 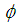 is onto of Y if the range of
is onto of Y if the range of 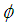 is Y.
is Y.2.7. Kernel of a Homomorphism
- If
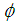 is a homomorphism of a group
is a homomorphism of a group 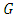 into
into 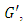 then the kernel of
then the kernel of 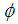 is denoted as
is denoted as 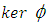 and is defined as
and is defined as 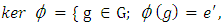 where
where 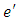 is the identity of
is the identity of 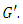
2.8. Linear Transformation
- Let
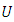 and
and 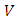 be two vector spaces over the same field
be two vector spaces over the same field 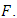 Then a mapping
Then a mapping 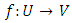 is called linear transformation of
is called linear transformation of 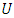 into
into 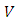 if
if 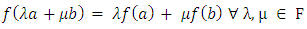 and
and 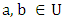 (Kenneth Hoffmann, 1971).
(Kenneth Hoffmann, 1971).2.9. Other Notations
- 1.
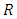 denotes the set of all real numbers.2.
denotes the set of all real numbers.2. 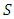 denote the set of all strongly magic squares of order
denote the set of all strongly magic squares of order 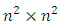 3.
3. 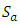 denote the set of all strongly magic squares of order
denote the set of all strongly magic squares of order 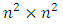 denote the set of all strongly magic squares of the form
denote the set of all strongly magic squares of the form 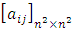 such that
such that 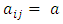 for every
for every 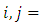
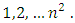 Here A is denoted as
Here A is denoted as 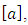 i.e. If
i.e. If 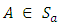 then
then 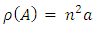 4.
4. 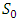 denote the set of all strongly magic squares of order
denote the set of all strongly magic squares of order 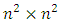 with magic constant 0, i.e. If
with magic constant 0, i.e. If 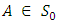 then
then 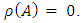
3. Propositions and Theorems
- Proposition 3.1If
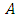 and
and 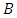 are two Strongly magic squares of order
are two Strongly magic squares of order 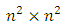 with
with 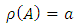 and
and 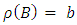 , then
, then 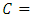
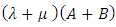 is also a Strongly magic square with magic constant
is also a Strongly magic square with magic constant 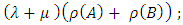 for every
for every 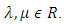 Proof:Let
Proof:Let 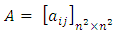 and
and 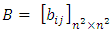 Then
Then 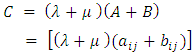 Sum of the ith row elements of
Sum of the ith row elements of 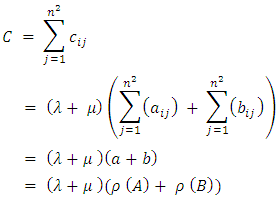 A similar computation holds for column sum, diagonals sum and sum of the
A similar computation holds for column sum, diagonals sum and sum of the  sub squares. From the above propositions the following results can be obtained by putting suitable values for
sub squares. From the above propositions the following results can be obtained by putting suitable values for  Results:If for every
Results:If for every 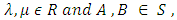
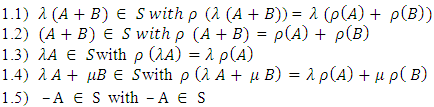 Theorem 3.2
Theorem 3.2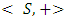 forms an abelian group. Proof:I. Closure property: if
forms an abelian group. Proof:I. Closure property: if 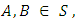 then
then 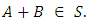 (from above result 1.2)II. Associativity: if
(from above result 1.2)II. Associativity: if 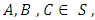 then
then 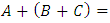
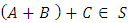 (Since matrix addition is associative.)III. Existence of Identity: There exists 0 matrix in
(Since matrix addition is associative.)III. Existence of Identity: There exists 0 matrix in 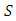 so that
so that 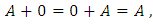 where 0 acts as the identity element.IV. Existence of additive inverse: For every
where 0 acts as the identity element.IV. Existence of additive inverse: For every 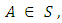 there exists
there exists 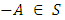 so that
so that 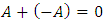 where
where 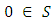 (from result 1.5).V. Commutativity: If
(from result 1.5).V. Commutativity: If 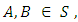 then
then 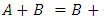
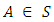 (Since matrix addition is commutative.)This completes the proof.Proposition 3.3
(Since matrix addition is commutative.)This completes the proof.Proposition 3.3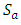 forms a subgroup of the abelian group
forms a subgroup of the abelian group 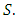 Proof:It is clear that
Proof:It is clear that 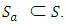 For
For 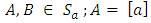 and
and 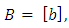 then clearly
then clearly 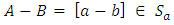 Thus
Thus 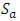 forms a subgroup of the abelian group
forms a subgroup of the abelian group 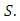 Proposition 3.4
Proposition 3.4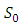 forms a subgroup of the abelian group
forms a subgroup of the abelian group 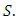 Proof:It is clear that
Proof:It is clear that 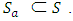 Take
Take 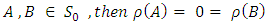 Now
Now 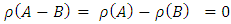 Therefore
Therefore 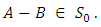 Thus
Thus 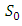 forms a subgroup of the abelian group
forms a subgroup of the abelian group 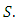 (Mallayya, Neeradha, 2016).Proposition 3.5For all
(Mallayya, Neeradha, 2016).Proposition 3.5For all 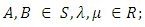
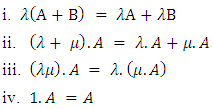 Proof:Since
Proof:Since 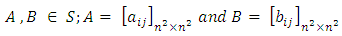
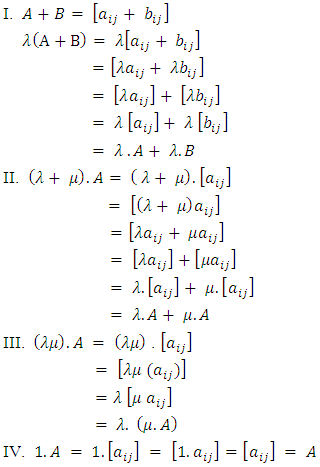 Theorem 3.6
Theorem 3.6 forms a vector space over the field of real numbers.Proof:It is an immediate consequence of Theorem 3.2 and Proposition 3.5Theorem 3.7
forms a vector space over the field of real numbers.Proof:It is an immediate consequence of Theorem 3.2 and Proposition 3.5Theorem 3.7 forms a vector space over the field of real numbers. Proof:Since
forms a vector space over the field of real numbers. Proof:Since  and
and  is a vector space over the field of real numbers
is a vector space over the field of real numbers 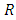 with respect to the addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication, it is enough to show that
with respect to the addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication, it is enough to show that 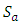 is a subspace of
is a subspace of 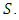 This can be verified by the fact; for every
This can be verified by the fact; for every 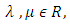 and
and 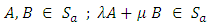
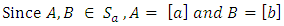
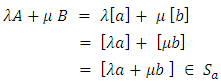 Theorem 3.8
Theorem 3.8 forms a vector space over the field of real numbers. Proof:Proceeding as in Proposition 3.7 it is enough to show thatfor every
forms a vector space over the field of real numbers. Proof:Proceeding as in Proposition 3.7 it is enough to show thatfor every 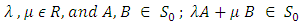 Since
Since 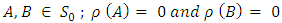 Now
Now 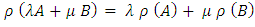 (From result 1.4)
(From result 1.4)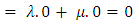 Thus
Thus 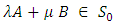 (Neeradha. C. K, V. Madhukar. Mallayya, 2016).Proposition 3.9The mapping
(Neeradha. C. K, V. Madhukar. Mallayya, 2016).Proposition 3.9The mapping 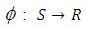 defined by
defined by 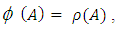
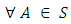 is a group homomorphism.Proof:Let
is a group homomorphism.Proof:Let 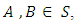 then
then 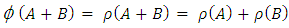 (By Result 1.2)
(By Result 1.2)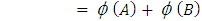 (Neeradha, Mallayya, 2016)Proposition 3.10The mapping
(Neeradha, Mallayya, 2016)Proposition 3.10The mapping 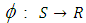 defined by
defined by 
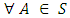 is a linear transformationProof:Let
is a linear transformationProof:Let 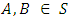
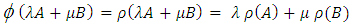 (By Result 1.4 and Theorem 3.6)
(By Result 1.4 and Theorem 3.6) 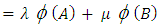 Proposition 3.11The mapping
Proposition 3.11The mapping 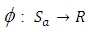 defined by
defined by 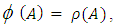
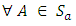 is a linear transformation.Proof:Let
is a linear transformation.Proof:Let 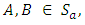 then
then 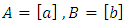 such that
such that  and
and 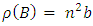 From Result 1.4 and Theorem 3.7
From Result 1.4 and Theorem 3.7 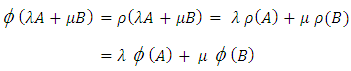 Hence
Hence  is a linear transformation.Proposition 3.12The mapping
is a linear transformation.Proposition 3.12The mapping 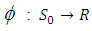 defined by
defined by 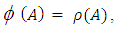
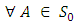 linear transformation.Let
linear transformation.Let 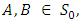 then
then 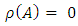 and
and 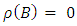
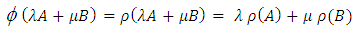 (By Result 1.4 and Theorem 3.8)
(By Result 1.4 and Theorem 3.8)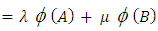 Hence
Hence 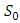 is a linear transformation.Proposition 3.13The kernel of the mapping
is a linear transformation.Proposition 3.13The kernel of the mapping 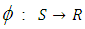 defined by
defined by 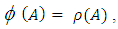
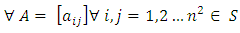 is Ker
is Ker 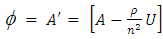 where
where 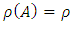 and
and 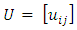 such that
such that 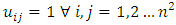 Proof:Let
Proof:Let 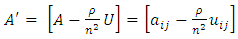
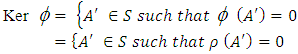 Now
Now 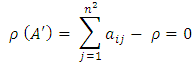 Therefore
Therefore 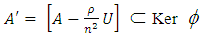 Now let
Now let 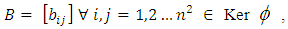 then
then 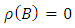 Clearly
Clearly 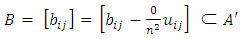 Therefore
Therefore 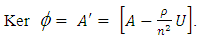 Theorem 3.14The mapping
Theorem 3.14The mapping 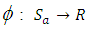 defined by
defined by 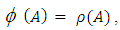
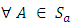 is a vector space isomorphism.Proof:Let
is a vector space isomorphism.Proof:Let 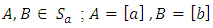 then
then 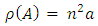 and
and 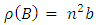 To show that
To show that 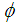 is 1-1
is 1-1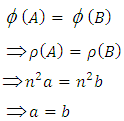 To show that
To show that 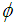 is ontoFor every
is ontoFor every 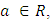 there exists
there exists 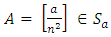 such that
such that 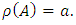 Since
Since 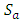 forms a vector space (from Theorem 3.7) and from the above shown results, the mapping
forms a vector space (from Theorem 3.7) and from the above shown results, the mapping 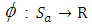 defined by
defined by 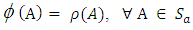 is a vector space isomorphism.
is a vector space isomorphism.4. Conclusions
- The study of strongly magic squares is an emerging innovative area in which mathematical analysis can be done. Here some advanced properties regarding strongly magic squares namely Abelian group structure, vector spaces, group homomorphism, group isomorphism, vector space isomorphism, linear transformation, kernel of transformation are described. Physical application of magic squares is still a new topic that needs to be explored more. Ollerenshaw and BrÈe (Ollerenshaw, 1999) have a patent for using most-perfect magic squares for cryptography, and Besslich (Besslich, 1983), (Besslich, Ph. W, 1983) has proposed using pan diagonal magic squares as dither matrices for image processing. Further studies are being carried out by the authors on the scope for further research and the application of Strongly Magic Squares on Diophantine equations, Moment of inertia, Electric Quadrapoles, Data hiding Schemes etc.
ACKNOWLEDGEMENTS
- We express sincere gratitude for the valuable suggestions given by Dr. Ramaswamy Iyer, Former Professor in Chemistry, Mar Ivanios College, Trivandrum, in preparing this paper.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML