Ndiyo Etop E.
Department of Mathematics, University of Uyo, Uyo, Nigeria
Correspondence to: Ndiyo Etop E., Department of Mathematics, University of Uyo, Uyo, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, the Schauder’s fixed point theorem is applied to establish an existence result for solution of second order impulsive differential inclusion. The findings show that there exists specific time at which the impulses effect of any dynamic evolutionary processes occur within a given interval.
Keywords:
Impulsive Differential Inclusions Existence, Evolutionary Process, Fixed Points, Galerkin’s Approximation
Cite this paper: Ndiyo Etop E., Existence Result for Solution of Second Order Impulsive Differential Inclusion to Dynamic Evolutionary Processes, American Journal of Mathematics and Statistics, Vol. 7 No. 2, 2017, pp. 89-92. doi: 10.5923/j.ajms.20170702.05.
1. Introduction
The dynamics of various evolutionary processes often undergo abrupt changes of state within intervals of continuous evolution. Over the years, differential equations had been used to model problems arising from physical phenomena and thereby bringing about solutions to such transformations. As at then, not much attention was given to physical, biological and economical processes, such issues like thresholds, bursting rhythms, optimal control models and pharmacokinetics which are processes known to exhibit abrupt changes at a given time-lag.In certain phenomenon, these changes are regarded as shocks, perturbations and natural disasters [1]. These perturbations because of its short term durations are rather better handled as having acted instantaneously in the form of impulses. Associated with this development, a theory of impulsive differential equations had been recently given attention [2-5].Researchers are now exploiting this idea of impulsive differential equations to handle other certain processes that involve hereditary issues such as population dynamics, ecology, chemical technology, biotechnology etc having greater functional analysis concept thus giving rise to functional differential equations [6, 7]. As an application of this theory, models for thresholds of malaria control when spraying occurs had been presented [8, 9].Despite the rapid attention to impulsive differential and partial differential equations and inclusions with fixed moments or fractional orders [4, 6, 2] cases for which the part governing the derivatives are not completely resolved.A dynamic process involving the derivative x’(t) of a state x(t) may be known only within a set S(t, x (t)) ⊂ 𝑹 formulated by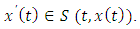 Differential inclusions arise more especially in models for control systems, game theory and biological systems.In this paper, the existence result for solution of dynamic evolutionary processes modeled using second order impulsive differential inclusions of the form
Differential inclusions arise more especially in models for control systems, game theory and biological systems.In this paper, the existence result for solution of dynamic evolutionary processes modeled using second order impulsive differential inclusions of the form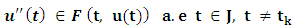 | (1.1) |
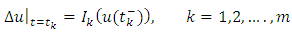 | (1.2) |
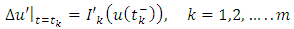 | (1.3) |
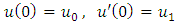 | (1.4) |
Where 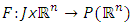 is multivalued map with compact values,
is multivalued map with compact values, 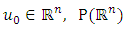 is the family of all subsets of
is the family of all subsets of 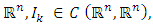
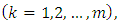
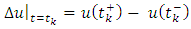 with
with 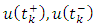 representing the right and left limits of u(t) at fixed moment
representing the right and left limits of u(t) at fixed moment 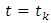 respectively, is established by applying the Schauder’s fixed point theorem.This paper is organized in three sections. In section two, some preliminaries and theorems are given. The main existence result is formulated and proved in section three. This paper further initiates the study of impulsive differential inclusions using Galerkin’s approximations.
respectively, is established by applying the Schauder’s fixed point theorem.This paper is organized in three sections. In section two, some preliminaries and theorems are given. The main existence result is formulated and proved in section three. This paper further initiates the study of impulsive differential inclusions using Galerkin’s approximations.
2. Preliminaries
In this section, notations, some basic definitions and some auxiliary results from multivalued analysis which are used in the sequel are presented and with some certain necessary assumptions.Let 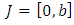 with
with 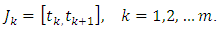 Consider the space of piece wise continuous functions defined by
Consider the space of piece wise continuous functions defined by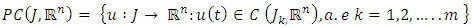 and the space of first order differentiable functions given by
and the space of first order differentiable functions given by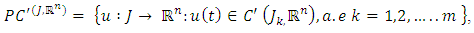 hold except for some
hold except for some 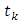 at which
at which 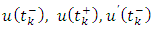 and
and 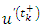 exist such that
exist such that 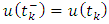 and
and 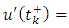
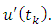 These sets of functions are Banach spaces with the norm:
These sets of functions are Banach spaces with the norm: 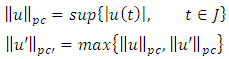 | (2.1) |
The space of all absolutely continuous functions are denoted by 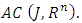 Definition 2.1: A function
Definition 2.1: A function 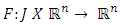 is said to beL’-caratheodory function if (i)
is said to beL’-caratheodory function if (i) 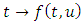 is measurable for each
is measurable for each 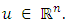 (ii)
(ii) 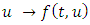 is continous for almost all
is continous for almost all 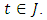 Definition 2.2: A multivalued map
Definition 2.2: A multivalued map 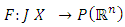 is said to be L’- caratheodory if (i)
is said to be L’- caratheodory if (i) 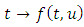 is measurable for each
is measurable for each 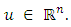 (ii)
(ii) 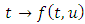 upper semicontinous on R for almost all
upper semicontinous on R for almost all 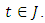 (iii) for each
(iii) for each 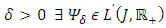 such that
such that 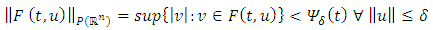 | (2.2) |
and t almost everywhere in 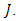 HypothesisLet ‘F’ be an
HypothesisLet ‘F’ be an 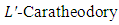 function, then H1: there exist constants
function, then H1: there exist constants 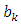 and
and 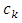 such that
such that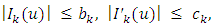
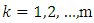 for each
for each 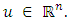 H2:
H2: 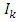 and
and 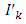 are Lipschitz continuous in that for
are Lipschitz continuous in that for 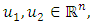
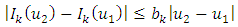 and
and 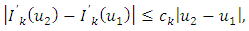
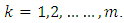 H3: there exist a constant
H3: there exist a constant 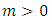 such that
such that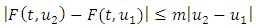 for each
for each 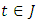 and
and 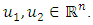 H4: there exist a continuous non-decreasing function
H4: there exist a continuous non-decreasing function 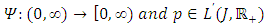 Such that
Such that 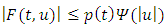 for
for 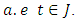 With
With 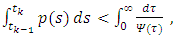
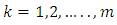 and
and 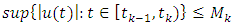 Theorem (2.1) (Schauder fixed point) [10, p 367]. Let Ω be a closed bounded and convex subset of the Banach space X and let
Theorem (2.1) (Schauder fixed point) [10, p 367]. Let Ω be a closed bounded and convex subset of the Banach space X and let 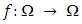 be continous and compact. Then f possesses at least one fixed point
be continous and compact. Then f possesses at least one fixed point 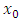 in
in 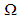 such that
such that 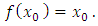 Lemma 2.1 [11] if
Lemma 2.1 [11] if 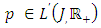 and
and 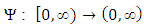 is non-decreasing with
is non-decreasing with 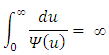 then the integral equation
then the integral equation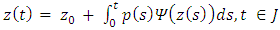 has for each
has for each 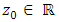 a unique solution z.If
a unique solution z.If 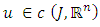 satisfies the integral in equality
satisfies the integral in equality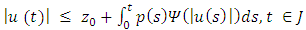 then
then 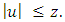
3. Main Result
Considering now the initial value problem of equations 1.1 – 1.4, our existence result concerns the a priori estimates on its possible solution.Definition 3.1:A given function 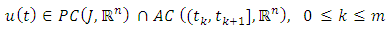 is called a solution of equation 1.1-1.4 if it satisfies the differential inclusion
is called a solution of equation 1.1-1.4 if it satisfies the differential inclusion 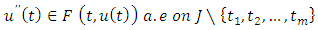 The Solution representation is given as
The Solution representation is given as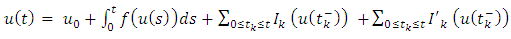 | (3.1) |
Lemma 3.1 Assume that the hypothesis H1-H4 are satisfied. Then the equation 1.1-1.4 has at least one solution.Proof: A solution to problem 1.1-1.4 is often assumed to be a fixed point of an operator of the form.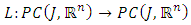 defined by
defined by 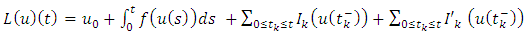 | (3.2) |
We show that L is a compact operator that is closed bounded and convex.Step 1: L is continuousLet 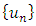 be a sequence such that
be a sequence such that 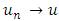 in
in 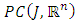 then
then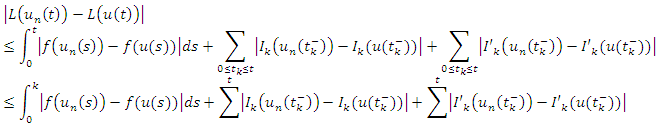 Since
Since 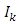 and
and 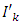 are continous and f is L’-Caratheodory, then
are continous and f is L’-Caratheodory, then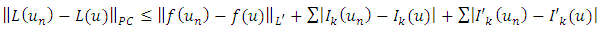 Hence
Hence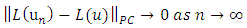 | (3.4) |
Step 2: L maps bounded sets into bounded set in 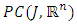 Let
Let 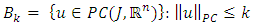 be a bounded set f
be a bounded set f 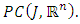 for each
for each 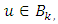 it is enough to show that there exist
it is enough to show that there exist 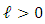 such that
such that 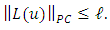 since
since 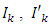 are continous and in particular Lipschitz’s continuous, we have that
are continous and in particular Lipschitz’s continuous, we have that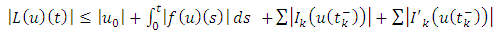 | (3.5) |
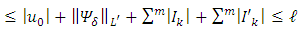 | (3.6) |
Step 3: L maps set into equicontinuous sets of the space 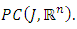 let
let 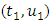 and
and 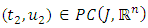 such that
such that 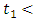
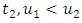 and
and  be a bounded set as defined above. Then
be a bounded set as defined above. Then 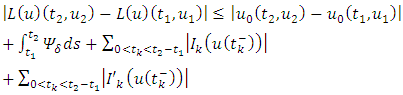 | (3.7) |
As 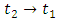 the right hand side of the inequality tends to zero
the right hand side of the inequality tends to zero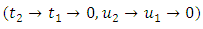 By applying the Arzela-Ascoli theorem it is clearly seen from the consequences of step 1- step 3 that L is compact and completely continuous. We state the result thus:The Existence TheoremSuppose that the lemma 3.1 and hypothesis H1-H4 are satisfied for
By applying the Arzela-Ascoli theorem it is clearly seen from the consequences of step 1- step 3 that L is compact and completely continuous. We state the result thus:The Existence TheoremSuppose that the lemma 3.1 and hypothesis H1-H4 are satisfied for 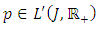 such that
such that 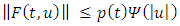
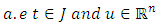 with
with 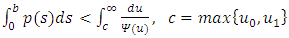
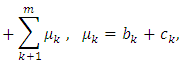 Then the impulsive differential inclusion 1.1-1.4 has at least a solution.Proof: since the operator L is compact, closed bounded and convex, by applying the Schauder’s fixed point theorem we consider the set
Then the impulsive differential inclusion 1.1-1.4 has at least a solution.Proof: since the operator L is compact, closed bounded and convex, by applying the Schauder’s fixed point theorem we consider the set 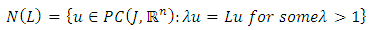 | (3.8) |
And we show that 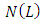 is bounded. Let
is bounded. Let 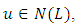 by definition we mean
by definition we mean 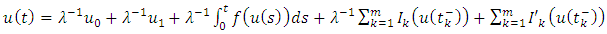 | (3.9) |
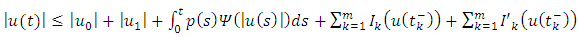 | (3.10) |
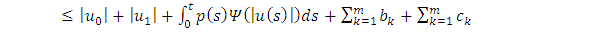 | (3.11) |
Let 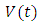 represent the right hand side of the inequality, then
represent the right hand side of the inequality, then 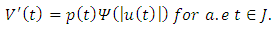 With
With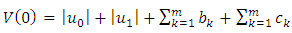 | (3.12) |
i.e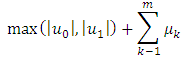 Since Ψ is non-decreasing function, we have that
Since Ψ is non-decreasing function, we have that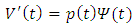 By theorem 1.4.2, p35 [1], we have that
By theorem 1.4.2, p35 [1], we have that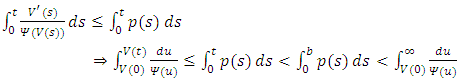 | (3.13) |
This equality indicates the existence of a constant 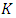 depending only on the functions
depending only on the functions 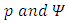 such that
such that 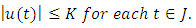 Hence
Hence 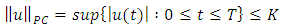 | (3.14) |
Thus  is bounded. We deduce therefore that
is bounded. We deduce therefore that 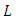 has a fixed point
has a fixed point 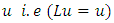 which is the solution.
which is the solution.
4. Conclusions
The Solution is considered at a point tk which is known and can be estimated. Thus, the solution to the problem exists by establishing or locating the point tk, where the solution representation is as given in 3.1. For further research, if the problem can be formulated in the finite dimensional space thus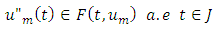 then applying Galerkin’s approximations of the solution and subsequent extension to the entire space, we assumed that the problem can be solved.
then applying Galerkin’s approximations of the solution and subsequent extension to the entire space, we assumed that the problem can be solved.
References
| [1] | V. Lakshmikantham, D. D. Bainov and P. S. Simeonov (1989): Theory of Impulsive Differential Equations (series in modern Applied maths vol. 6), World scientific, singapore. |
| [2] | A. M. Samoilenko and N.A Perestyuk (1995): Impulsive differential equations, World scientific, Singapore. |
| [3] | M. Benchohra, J. Henderson and S. Ntouyas (2006): Impulsive Differential Equations and Inclusions (contemporary maths and its application vol. 2) Hindawi publishing co-operation, New York. |
| [4] | M. Benchohra, B. A Slimnani (2009): Existence and Uniqueness of solutions to impulsive fractional differential equations. Elec. J. Diff. Eqn (2009) No. 10. |
| [5] | M. Benchohra and D. Seba (2011): Impulsive Partial hyperbolic fractional order diff. eqns in Banach s;paces. Jour. Of fractional calculus and Applications vol 1 (4):1-12. |
| [6] | M. Benchohra, J. Henderson and D. Seba (2008): Measure of non-compactness and fractional differential equations in Banach spaces. Common. Appl. Dual 12 (2008) no. 40; 419-428. |
| [7] | [M. Benchohra, J. Henderson, S. K. Ntouyas and A. ouahab (2008): Existence results for functional differential Equations of fractional order. J. maths Dual Appl 338 (2008) 1340-1350. |
| [8] | Mo’tassem AL-ARYDAH and Robert Smith? (2011): controlling malaria with indoor Residual spraying in spatially heterogeneous environments Aims Journal (To appear). |
| [9] | R.J. Smith and S.D Hove-musekwa (2008): Determining effective spraying periods to control malaria via indoor residual spraying in sub-saharan Africa. Journal of Applied maths and Decision sciences (2008) ID 45463. |
| [10] | Wloka J. (1987): Partial Differential Equation, University press, cambrigde. |
| [11] | S. Heikkila and V. Lakshmikantham (1994): Monotone iterative Techniques for Discontinous non-linear Differential Equality Monographs and Textbook in Pure and Applied maths vol. 181, marcel Dekker, New York. |



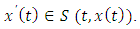 Differential inclusions arise more especially in models for control systems, game theory and biological systems.In this paper, the existence result for solution of dynamic evolutionary processes modeled using second order impulsive differential inclusions of the form
Differential inclusions arise more especially in models for control systems, game theory and biological systems.In this paper, the existence result for solution of dynamic evolutionary processes modeled using second order impulsive differential inclusions of the form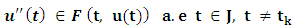
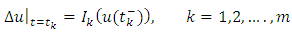
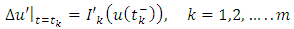
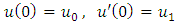
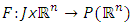 is multivalued map with compact values,
is multivalued map with compact values, 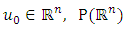 is the family of all subsets of
is the family of all subsets of 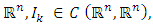
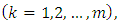
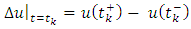 with
with 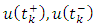 representing the right and left limits of u(t) at fixed moment
representing the right and left limits of u(t) at fixed moment 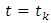 respectively, is established by applying the Schauder’s fixed point theorem.This paper is organized in three sections. In section two, some preliminaries and theorems are given. The main existence result is formulated and proved in section three. This paper further initiates the study of impulsive differential inclusions using Galerkin’s approximations.
respectively, is established by applying the Schauder’s fixed point theorem.This paper is organized in three sections. In section two, some preliminaries and theorems are given. The main existence result is formulated and proved in section three. This paper further initiates the study of impulsive differential inclusions using Galerkin’s approximations.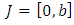 with
with 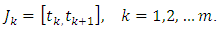 Consider the space of piece wise continuous functions defined by
Consider the space of piece wise continuous functions defined by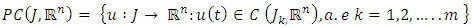 and the space of first order differentiable functions given by
and the space of first order differentiable functions given by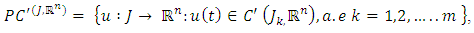 hold except for some
hold except for some 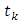 at which
at which 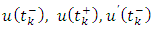 and
and 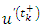 exist such that
exist such that 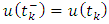 and
and 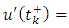
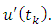 These sets of functions are Banach spaces with the norm:
These sets of functions are Banach spaces with the norm: 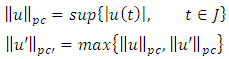
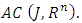 Definition 2.1: A function
Definition 2.1: A function 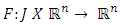 is said to beL’-caratheodory function if (i)
is said to beL’-caratheodory function if (i) 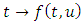 is measurable for each
is measurable for each 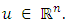 (ii)
(ii) 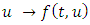 is continous for almost all
is continous for almost all 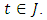 Definition 2.2: A multivalued map
Definition 2.2: A multivalued map 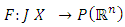 is said to be L’- caratheodory if (i)
is said to be L’- caratheodory if (i) 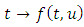 is measurable for each
is measurable for each 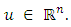 (ii)
(ii) 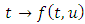 upper semicontinous on R for almost all
upper semicontinous on R for almost all 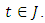 (iii) for each
(iii) for each 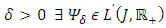 such that
such that 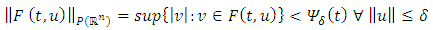
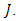 HypothesisLet ‘F’ be an
HypothesisLet ‘F’ be an 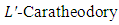 function, then H1: there exist constants
function, then H1: there exist constants 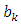 and
and 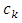 such that
such that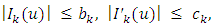
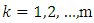 for each
for each 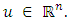 H2:
H2: 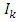 and
and 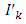 are Lipschitz continuous in that for
are Lipschitz continuous in that for 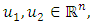
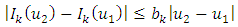 and
and 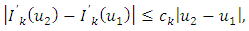
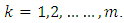 H3: there exist a constant
H3: there exist a constant 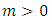 such that
such that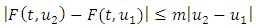 for each
for each 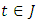 and
and 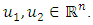 H4: there exist a continuous non-decreasing function
H4: there exist a continuous non-decreasing function 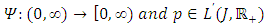 Such that
Such that 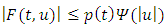 for
for 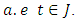 With
With 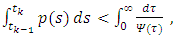
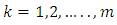 and
and 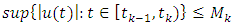 Theorem (2.1) (Schauder fixed point) [10, p 367]. Let Ω be a closed bounded and convex subset of the Banach space X and let
Theorem (2.1) (Schauder fixed point) [10, p 367]. Let Ω be a closed bounded and convex subset of the Banach space X and let 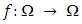 be continous and compact. Then f possesses at least one fixed point
be continous and compact. Then f possesses at least one fixed point 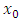 in
in 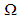 such that
such that 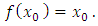 Lemma 2.1 [11] if
Lemma 2.1 [11] if 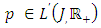 and
and 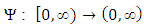 is non-decreasing with
is non-decreasing with 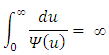 then the integral equation
then the integral equation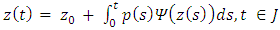 has for each
has for each 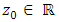 a unique solution z.If
a unique solution z.If 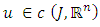 satisfies the integral in equality
satisfies the integral in equality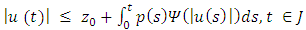 then
then 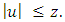
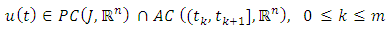 is called a solution of equation 1.1-1.4 if it satisfies the differential inclusion
is called a solution of equation 1.1-1.4 if it satisfies the differential inclusion 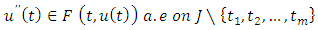 The Solution representation is given as
The Solution representation is given as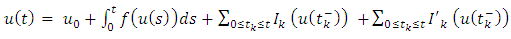
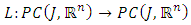 defined by
defined by 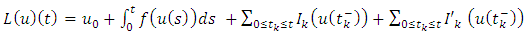
 be a sequence such that
be a sequence such that 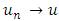 in
in 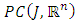 then
then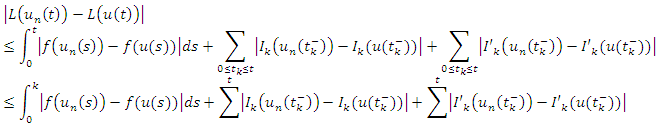 Since
Since 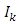 and
and 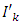 are continous and f is L’-Caratheodory, then
are continous and f is L’-Caratheodory, then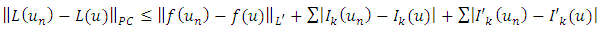 Hence
Hence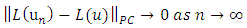
 Let
Let 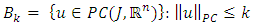 be a bounded set f
be a bounded set f 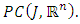 for each
for each 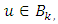 it is enough to show that there exist
it is enough to show that there exist 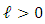 such that
such that 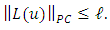 since
since 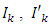 are continous and in particular Lipschitz’s continuous, we have that
are continous and in particular Lipschitz’s continuous, we have that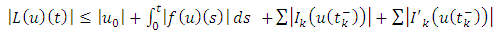
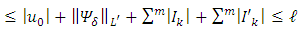
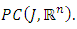 let
let 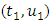 and
and 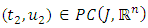 such that
such that 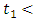
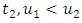 and
and 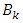 be a bounded set as defined above. Then
be a bounded set as defined above. Then 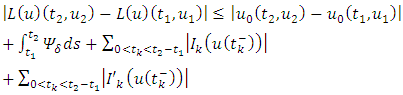
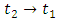 the right hand side of the inequality tends to zero
the right hand side of the inequality tends to zero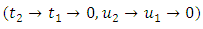 By applying the Arzela-Ascoli theorem it is clearly seen from the consequences of step 1- step 3 that L is compact and completely continuous. We state the result thus:The Existence TheoremSuppose that the lemma 3.1 and hypothesis H1-H4 are satisfied for
By applying the Arzela-Ascoli theorem it is clearly seen from the consequences of step 1- step 3 that L is compact and completely continuous. We state the result thus:The Existence TheoremSuppose that the lemma 3.1 and hypothesis H1-H4 are satisfied for 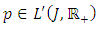 such that
such that 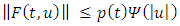
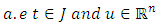 with
with 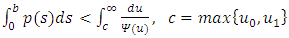
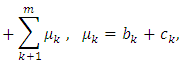 Then the impulsive differential inclusion 1.1-1.4 has at least a solution.Proof: since the operator L is compact, closed bounded and convex, by applying the Schauder’s fixed point theorem we consider the set
Then the impulsive differential inclusion 1.1-1.4 has at least a solution.Proof: since the operator L is compact, closed bounded and convex, by applying the Schauder’s fixed point theorem we consider the set 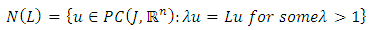
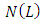 is bounded. Let
is bounded. Let 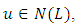 by definition we mean
by definition we mean 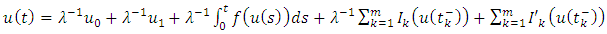
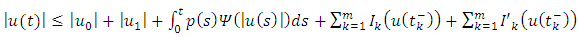
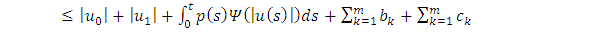
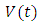 represent the right hand side of the inequality, then
represent the right hand side of the inequality, then 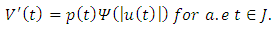 With
With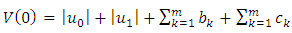
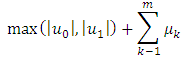 Since Ψ is non-decreasing function, we have that
Since Ψ is non-decreasing function, we have that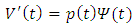 By theorem 1.4.2, p35 [1], we have that
By theorem 1.4.2, p35 [1], we have that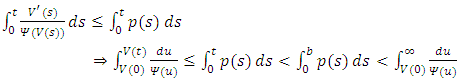
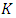 depending only on the functions
depending only on the functions  such that
such that 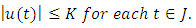 Hence
Hence 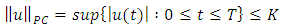
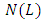 is bounded. We deduce therefore that
is bounded. We deduce therefore that  has a fixed point
has a fixed point 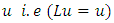 which is the solution.
which is the solution.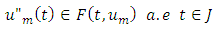 then applying Galerkin’s approximations of the solution and subsequent extension to the entire space, we assumed that the problem can be solved.
then applying Galerkin’s approximations of the solution and subsequent extension to the entire space, we assumed that the problem can be solved. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML