-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2017; 7(2): 71-77
doi:10.5923/j.ajms.20170702.03

Weighted Robust Lasso and Adaptive Elastic Net Method for Regularization and Variable Selection in Robust Regression with Optimal Scaling Transformations
Tarek M. Omara
Department of Statistics, Mathematics and Insurance, Faculty of Commerce, Kafrelsheikh University, Kafrelsheikh, Egypt
Correspondence to: Tarek M. Omara, Department of Statistics, Mathematics and Insurance, Faculty of Commerce, Kafrelsheikh University, Kafrelsheikh, Egypt.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, the weight least absolute deviation adaptive lasso optimal scaling method (WLAD-CATREG adaptive lasso) and weight least absolute deviation adaptive elastic net regression with optimal scaling method (WLAD-CATREG adoptive elastic net) will introduced, which is combined of weight least absolute deviation regression (WLAD-CATREG) and adaptive lasso (A-Lasso) or adaptive elastic net regression (A-Elastic net) with optimal scaling. Thus (WLAD-CATREG adoptive elastic net) method aim to automatically select variable, aspire to gropes effect and erase the bad effect of leverage points and outliers simultaneously, these aims cannot be achieved by (WLAD-CATREG), adaptive lasso regression (A-Lasso), weight robust adaptive lasso regression (WLAD-CATREG adoptive lasso), Weight least absolute deviation elastic net regression (WLAD-CATREG elastic net). Simulation study will be running to validated superiority of the (WLAD-CATREG adoptive Lasso) and (WLAD-CATREG adoptive elastic net).
Keywords: A-Lasso, A-Elastic net, WLAD-CATREG, LAD-adoptive lasso, WLAD-CATREG adoptive lasso, WLAD-CATREG adoptive elastic net
Cite this paper: Tarek M. Omara, Weighted Robust Lasso and Adaptive Elastic Net Method for Regularization and Variable Selection in Robust Regression with Optimal Scaling Transformations, American Journal of Mathematics and Statistics, Vol. 7 No. 2, 2017, pp. 71-77. doi: 10.5923/j.ajms.20170702.03.
Article Outline
1. Introduction
- In regression models, if the variables are categorical variables, the relation between independent and dependent variables will be nonlinear. In this case, we used optimal scaling to transforming categorical variables to numeric variables, thus regression model becomes linear. This transform is done in simultaneous with the estimate parameters. The ordinary least squirt (OLS) is common method for estimating regression model but it sensitively to the outliers. In the case of regression model with optimal scaling transformations the effects of outliers can be as yet large (Peter (1993)), thus robust regression is suitable alternative. The robust regression include several methods one of them least absolute deviation (LAD) regression method which used to deal with outliers. This method developed to deal with leverage point (outlier in independent variables) by use weights which effect only on leverage point. In this side, weight least absolute deviation (WLAD) regression method proposed by (Giloni et al., 2006a, b, Olcay 2011). The regression model possibly is suffered from variable select problem, thus lasso regression method (Tibshirani (1996)) is appropriate because it does shrinkage parameter and variable selection simultaneously. The same tuning parameter was used in lasso regression for all coefficient, so it suffered an palpable bias and not have the oracle properties. (Fan and Li (2001)), therefor adaptive lasso regression (A-Lasso) was used to allow several tuning parameters for several coefficients ((Zou (2006)), Hansheng et al. (2006)). To avoid outlier, adaptive lasso (A-Lasso) objective function been modified in to least absolute deviation adaptive lasso regression (LAD-adoptive lasso) which has oracle properties when we appropriately chosen tuning parameter (Hansheng et al. (2006) and Xu and Yin (2010)) and to avoid leverage points, (LAD-adoptive lasso) combined of weight least absolute deviation regression (WLAD) and adaptive lasso regression (A-lasso) (Olcay, 2011).The lasso regression has limitation when p » n, and if there is a group of highly correlated covariates, the lasso select one variable form the group, therefore (Zou and Hastie (2005)) introduce elastic net regression which basically combined penalty of ridge and lasso (L1, L2) and has not an oracle properties. The elastic net does shrinkage parameter, variable selection and aspire to group effect simultaneously. To improve the elastic net (Samiran, 2007) combined of the adaptive lasso and elastic net and get adaptive elastic net which have the oracle property when p » n. In this paper, for categorical regression model, we introduce new estimators (WLAD- CATREG adoptive elastic net) which considered appropriate way to deal with both leverage points and outliers, select variable and groping correlated variable simultaneously when p » n.
2. WLAD-CATREG Adoptive Lasso, WLAD-CATREG Adaptive Elastic Net
- Consider the categorical regression model (CATREG)
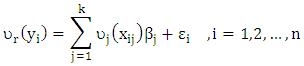 | (1) |
 is the discretized predictor variables,
is the discretized predictor variables,  is the function of transformation response variable,
is the function of transformation response variable, 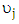 is the function of transform predictor variables,
is the function of transform predictor variables, 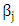 are the regression coefficients and
are the regression coefficients and 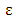 is independent random error. The form of the last transformation based on optical scaling, so in the case of numerical scaling level the result of CATREG is the same of standardized multiple linear regression (Anita and van (2007)). The (OLS) is the more commonly used for estimating the previous model. But this method is poorly when the model have outliers, thus many robust methods introduced. One important of the robust method called LpCATREG regression methods. Since
is independent random error. The form of the last transformation based on optical scaling, so in the case of numerical scaling level the result of CATREG is the same of standardized multiple linear regression (Anita and van (2007)). The (OLS) is the more commonly used for estimating the previous model. But this method is poorly when the model have outliers, thus many robust methods introduced. One important of the robust method called LpCATREG regression methods. Since 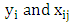 are standardized variables and if we fixed
are standardized variables and if we fixed 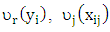 and
and 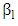 for all predictors l≠j then Lp is written as
for all predictors l≠j then Lp is written as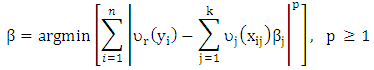 | (2) |
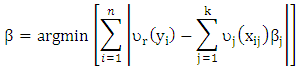 | (3) |
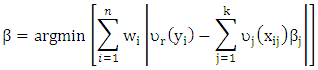 | (4) |
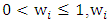 i=1,2,… ,n is the weights which will be chosen to breakdown leverage points. Chatterjee and Hadi, (1988) suggested weight depended of clean subset where
i=1,2,… ,n is the weights which will be chosen to breakdown leverage points. Chatterjee and Hadi, (1988) suggested weight depended of clean subset where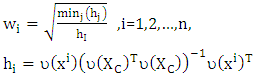
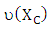 is clean subset,
is clean subset, 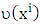 is the set of observation relative to clean subset. The discreet choice of weight lead to (WALD) estimator with fast computationally and high breakdown point. (Rousseeuw and Hubert (1997), (Olcay, 2011).) Used the robust distances (RD) to compute weights
is the set of observation relative to clean subset. The discreet choice of weight lead to (WALD) estimator with fast computationally and high breakdown point. (Rousseeuw and Hubert (1997), (Olcay, 2011).) Used the robust distances (RD) to compute weights 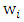 which defined as
which defined as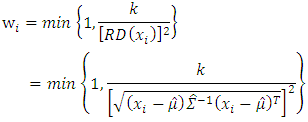 | (5) |
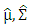 are location and scatter estimators. Since robust distances (RD) identify leverage points increasing, (RD) lead to decrease weights
are location and scatter estimators. Since robust distances (RD) identify leverage points increasing, (RD) lead to decrease weights 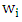 and thus leverage points corresponds to similar weights then it will be down weighted.(Tibshirani (1996)) introduce lasso regression to combines estimate and variable selection. The lasso regression depend on minimize least squirt regression with the L1 norm condition. An extinction lasso regression, (Anita and van (2007)) introduce lasso penalties with (CATREG)
and thus leverage points corresponds to similar weights then it will be down weighted.(Tibshirani (1996)) introduce lasso regression to combines estimate and variable selection. The lasso regression depend on minimize least squirt regression with the L1 norm condition. An extinction lasso regression, (Anita and van (2007)) introduce lasso penalties with (CATREG)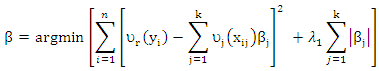 | (6) |
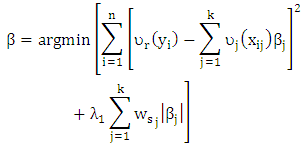 | (7) |
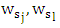 is two weight vector,
is two weight vector, 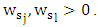 In order to reach oracle property, ((Zou (2006), Olcay (2011)) define the weight vector as
In order to reach oracle property, ((Zou (2006), Olcay (2011)) define the weight vector as 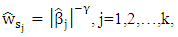 Where
Where 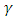 is a positive constant and
is a positive constant and 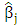 is an elastic net estimater of
is an elastic net estimater of 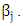 (Zou and Zhang (2009)) used the other formula for weight vector as
(Zou and Zhang (2009)) used the other formula for weight vector as 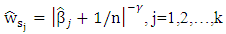 and (Wang et al (2007)) choose
and (Wang et al (2007)) choose  as
as 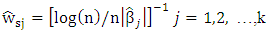 | (8) |
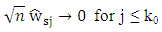 and
and 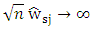 for j > k0 to avoid dividing zeros.Since least squirt errors sensitive to outliers, (Hansheng and Chenlei. (2006)), introduced least absolute deviation adaptive lasso regression (LAD-adoptive lasso). In this way, (Olcay (2011)) introduce weight least absolute deviation regression (WLAD) and adaptive lasso regression (A-lasso) to avoid leverage point add to the features of (LAD-adoptive lasso) which produce robust parameter with oracle property and select variables. The (WLAD-adoptive lasso) with (CATREG) (New) get as
for j > k0 to avoid dividing zeros.Since least squirt errors sensitive to outliers, (Hansheng and Chenlei. (2006)), introduced least absolute deviation adaptive lasso regression (LAD-adoptive lasso). In this way, (Olcay (2011)) introduce weight least absolute deviation regression (WLAD) and adaptive lasso regression (A-lasso) to avoid leverage point add to the features of (LAD-adoptive lasso) which produce robust parameter with oracle property and select variables. The (WLAD-adoptive lasso) with (CATREG) (New) get as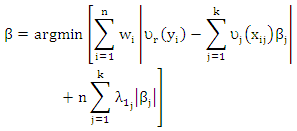 | (9) |
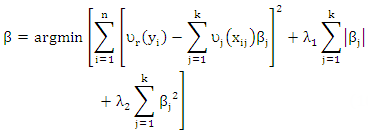 | (10) |
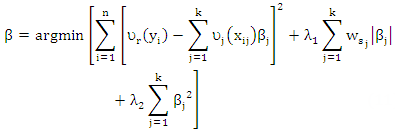 | (11) |
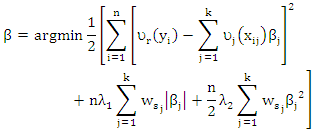 | (12) |
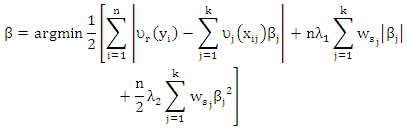 | (13) |
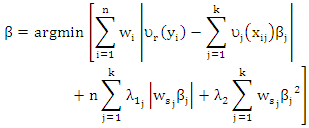 | (14) |
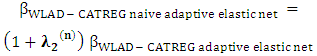 | (15) |
3. Algorithm
- To simplify (13), let
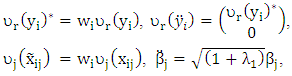 and define
and define 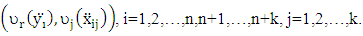 Where
Where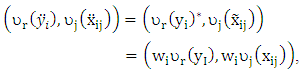
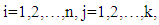
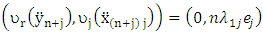
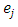 is a p-dimension vector with jth term equals one and all others equal to zero. We can rewrite (13) as a form of ridge as
is a p-dimension vector with jth term equals one and all others equal to zero. We can rewrite (13) as a form of ridge as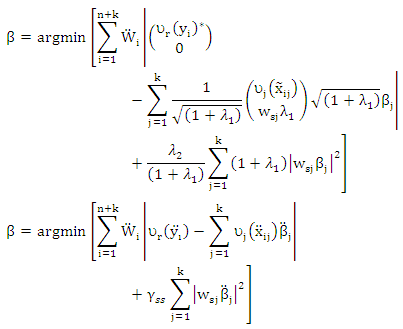 Where
Where 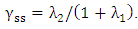 Define
Define 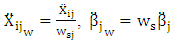 Then
Then 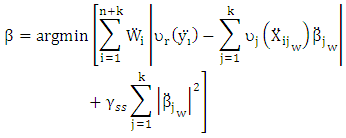 | (16) |
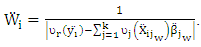 Before computing the WLAD-CATREG adaptive elastic net we must choose the weights
Before computing the WLAD-CATREG adaptive elastic net we must choose the weights 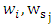 by use (and the tuning parameters
by use (and the tuning parameters 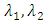 can be chosen Cross-validation (CV) on a two-dimensional but it would be computationally prohibitive (See Li and Jia (2010)).So that we fixed
can be chosen Cross-validation (CV) on a two-dimensional but it would be computationally prohibitive (See Li and Jia (2010)).So that we fixed 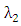 and we used five-fold Absolute Cross-validation (ACV) to select tuning parameter
and we used five-fold Absolute Cross-validation (ACV) to select tuning parameter 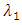 which avoided leverage point. The Absolute Cross-validation (ACV) defined as
which avoided leverage point. The Absolute Cross-validation (ACV) defined as 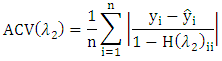 Where
Where 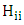 is hat matrix,
is hat matrix, 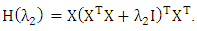 We chosen weights
We chosen weights 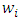 by the robust distances (RD) which defined as (5).We computation the WLAD-CATREG adaptive elastic net by development the algorithm:
by the robust distances (RD) which defined as (5).We computation the WLAD-CATREG adaptive elastic net by development the algorithm:
4. The Properties of Estimators
- In this section, we discuss the asymptotic properties of the WLAD-CATREG adaptive adaptive elastic net At the first, we rooting some convenience and definitions. We decompose the
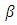 vector as
vector as decompose the predictor variables
decompose the predictor variables 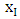 as
as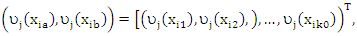
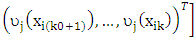 Defined
Defined 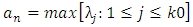 and
and 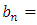
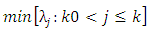 where
where 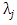 is a function of n. (Wang and Leng (2007)).Let
is a function of n. (Wang and Leng (2007)).Let 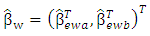 be identical WLAD-CATREG adoptive net elastic estimator. Consider the linear regression model (1) with independent and assume the following conditions:A1: The identically error with median zero and cumulative distribution function F which is positive and continues, A2: The covariance of predictor variables
be identical WLAD-CATREG adoptive net elastic estimator. Consider the linear regression model (1) with independent and assume the following conditions:A1: The identically error with median zero and cumulative distribution function F which is positive and continues, A2: The covariance of predictor variables 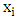 exists and positive definiteA3: W is n×n diagonal matrix with known positive value (wi ,i=1,2,...,n), max wi =O(1) and max wi-1 = O(1)
exists and positive definiteA3: W is n×n diagonal matrix with known positive value (wi ,i=1,2,...,n), max wi =O(1) and max wi-1 = O(1)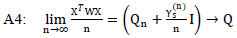 where Q is a positive definite.
where Q is a positive definite.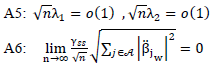 The assumes (A1, A3, A4) are the same assumes for Olcay (2011), the assume (A4) is the (A6) assume for (Zou and Zhang (2009)) and the assumes A1, A2 the same assume for (Pollard, 1991). Lemma (1): For the model (1), if it satisfies Assumptions A1: A6, then LAD-CATREG adaptive elastic net
The assumes (A1, A3, A4) are the same assumes for Olcay (2011), the assume (A4) is the (A6) assume for (Zou and Zhang (2009)) and the assumes A1, A2 the same assume for (Pollard, 1991). Lemma (1): For the model (1), if it satisfies Assumptions A1: A6, then LAD-CATREG adaptive elastic net 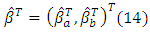 must satisfies the following:
must satisfies the following: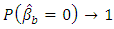
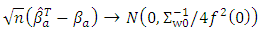 Proof lemma (1):Let
Proof lemma (1):Let 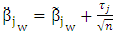 Then, we can rewrite (14) as
Then, we can rewrite (14) as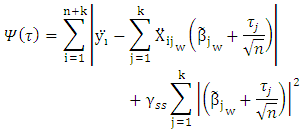
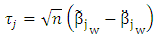
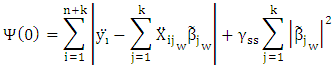
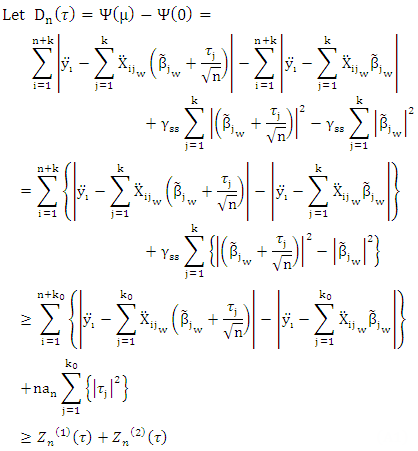 | (A1) |
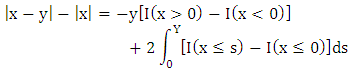 Using this equation, the first item at (A1)
Using this equation, the first item at (A1) 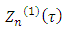 can be expressed as
can be expressed as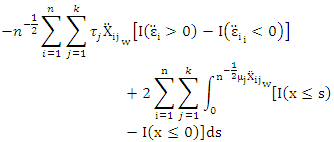 | (A2) |
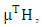 where
where 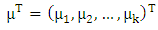 and H p-dimensional normal random vector with mean 0 and variance matrix
and H p-dimensional normal random vector with mean 0 and variance matrix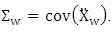 Since
Since 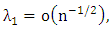
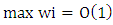 and
and 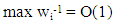 then
then 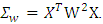 Follow from the proofs of lemma1 (Wang et al. (2007)), the second item converges to
Follow from the proofs of lemma1 (Wang et al. (2007)), the second item converges to 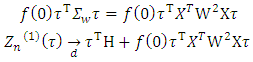 Since
Since 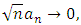 the second item at (A1)
the second item at (A1) 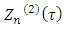 converges to 0 in probability.Then
converges to 0 in probability.Then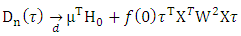 Where
Where 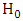 p-dimensional normal random vector with mean 0 and variance matrix
p-dimensional normal random vector with mean 0 and variance matrix 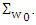 Follow from the proofs of lemma1 (Wang et al. (2007)).
Follow from the proofs of lemma1 (Wang et al. (2007)).5. The Simulation Study
- In this section, the performance of the WLAD-CATREG adaptive elastic net estimates are examined via the simulation. We simulate data sets from the true model
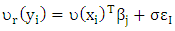 where
where 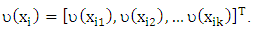 To ensure the situation of grouping variable, the simulated date consist of a training set, an independent validation set and an independent test set. In this simulate, we use the 50 simulated data sets each consisting of (30 training set/30 independent validation set /100 independent test set) observations and have 30 variables, 10 categorical variables each of them containing nine category and 20 numerical variables. The numerical variables generate
To ensure the situation of grouping variable, the simulated date consist of a training set, an independent validation set and an independent test set. In this simulate, we use the 50 simulated data sets each consisting of (30 training set/30 independent validation set /100 independent test set) observations and have 30 variables, 10 categorical variables each of them containing nine category and 20 numerical variables. The numerical variables generate 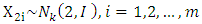 recalling to the model
recalling to the model 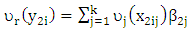 where
where 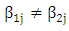 and the categorical variables generate by Bernoulli distribution with nine category. The correlation between pairs of variables
and the categorical variables generate by Bernoulli distribution with nine category. The correlation between pairs of variables 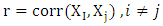 was taken (0.20, 0.60). We have used WLAD-CATREG-l algorithm to compute the LAD-adaptive lasso estimator and WLAD-CATREG adaptive lasso estimator and WLAD-CATREG-EN algorithm to compute the LAD-CATREG adaptive elastic net estimator and WLAD-CATREG adaptive elastic net estimator. To contaminate the data, we generated the contamination rate (ë= 20%, 40%). We will choose the place of outliers from observations on are works well. And the elastic net -CATREG methods select more variables than the lasso methods. In adding, the WLAD naïve adoptive elastic net-CATREG make improvements to a number of selected variables. categorical variable randomly and replacing the category on the variables by extreme values (such as 1 or 9) and will generate the outliers on numerical variable by
was taken (0.20, 0.60). We have used WLAD-CATREG-l algorithm to compute the LAD-adaptive lasso estimator and WLAD-CATREG adaptive lasso estimator and WLAD-CATREG-EN algorithm to compute the LAD-CATREG adaptive elastic net estimator and WLAD-CATREG adaptive elastic net estimator. To contaminate the data, we generated the contamination rate (ë= 20%, 40%). We will choose the place of outliers from observations on are works well. And the elastic net -CATREG methods select more variables than the lasso methods. In adding, the WLAD naïve adoptive elastic net-CATREG make improvements to a number of selected variables. categorical variable randomly and replacing the category on the variables by extreme values (such as 1 or 9) and will generate the outliers on numerical variable by 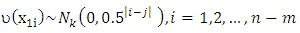 where
where 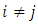 recalling to the model
recalling to the model 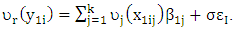 To ensure the achievement the normality of error with the possibility of the existence of outlier of y, we generate
To ensure the achievement the normality of error with the possibility of the existence of outlier of y, we generate 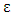 from t distribution with two degrees of freedoms
from t distribution with two degrees of freedoms 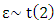 and set
and set 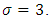 We let
We let and for the weight vector, we assume
and for the weight vector, we assume 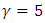 Since elastic parameters have two tuning parameters, we used 2-dimensional cross-validation. For this method, we use
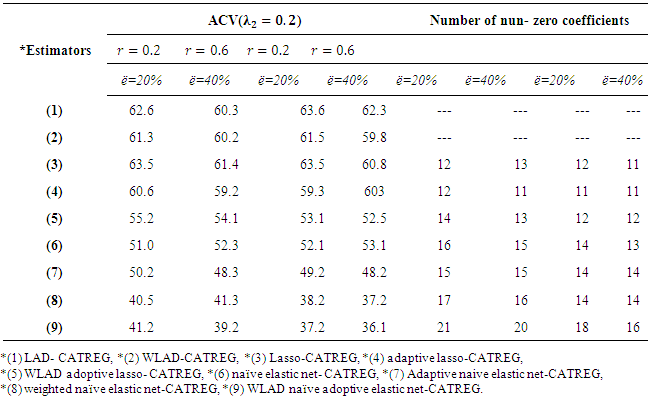
Since elastic parameters have two tuning parameters, we used 2-dimensional cross-validation. For this method, we use 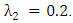 In Table (1), the WLAD-CATREG method has a poor performance especially at high level of correlation and lasso-CATREG has working poor at high level of outliers. Parallel, the weighted naïve elastic net-CATREG and WLAD naïve adoptive elastic net-CATREG method have a best performance. In all cases, elastic net methods are more improved than lasso methods and the weight was given to improve the estimate methods. When the level of correlation and the level of outliers are increase, the elastic estimators.
In Table (1), the WLAD-CATREG method has a poor performance especially at high level of correlation and lasso-CATREG has working poor at high level of outliers. Parallel, the weighted naïve elastic net-CATREG and WLAD naïve adoptive elastic net-CATREG method have a best performance. In all cases, elastic net methods are more improved than lasso methods and the weight was given to improve the estimate methods. When the level of correlation and the level of outliers are increase, the elastic estimators.
|
6. Conclusions
- We presented a new estimator for categorical regression model (CATREG) which takes into account effect the outliers, leverage point and variable select problem. The new criterion, Absolute Cross-validation (ACV) which use Cross-validation at robust form, was used for trade-off between estimators. The result for simulation study showed that, the weighted naïve elastic net-CATREG and the WLAD naïve adoptive elastic net-CATREG make improvements for the estimate.
References
| [1] | Peter, V. (1993), “M-estimators in multiple regression with optimal scaling”, Netherlands organization for scientific research, RR-92-10. |
| [2] | Giloni, A., Simonoff, J., Sengupta, B., (2006a), “Robust weighted LAD regression”, Computional Statistics & Data Analysis, Vol.50. |
| [3] | Giloni, A., Sengupta, B., Simonoff, J., (2006b), “A mathematical programming approach for improving the robustness of least sum of ansolute deviations regression”, Wiley InferScience doi, Vol.10. |
| [4] | Olcay A., (2011), "Weighted LAD-LASSO method for robust parameter estimation and variable selection in regression", Computational Statistics & Data Analysis, Vo.56. |
| [5] | Tibshirani, R. (1996), “Regression shrinkage and selection Via the lasso”, Journal of Royal Statistical Society B, Vo.58. |
| [6] | Fan, J., and Li, R., (2001), “Variable selection via nonconcave penalized likelihood and its oracle properties”, Journal of the American Statistical Association, Vo. 96. |
| [7] | Zou, H., (2006), “The adaptive Lasso and its oracle properties”, Journal of the American Statistical Association”, Vo. 101. |
| [8] | Hansheng W., Chenlei L., (2006), "A note on adaptive group lasso", Computational Statistics and Data Analysis, Vo.52. |
| [9] | Xu J., Yi Z., (2010), "Simultaneous estimation and variable selection in median regression using Lasso-type penalty", Annals of the institute of Statistical Mathematics, Vo.62. |
| [10] | Zou, H. and Hastie, T., (2005), “Regularization and variable selection via the elastic net”. Journal of the Royal Statistical Society, Series B, Vo.67. |
| [11] | Samiran G., (2007), "Adaptive Elastic Net: An Improvement of Elastic Net to achieve Oracle Properties", http://www.math.iupui.edu/research/preprint/2007/p07-01.pdf. |
| [12] | Anita J., Van d., (2007), "Prediction Accuracy and Stability of Regression with Optimal Scaling Transformations", https://www.researchgate.net/publication/28648961. |
| [13] | Rousseeuw p. and Leroy A., (1987), "Robust Regression and Outlier Detection", New York: John Wiley. |
| [14] | Ellis, S., Morgenthaler, S., (1992), "Leverage and break down in L1 regression", Journal of the American Statistical Association Vo. 87. |
| [15] | Chatterjee, S. and Hadi, A.S. (1988), Sensitivity Analysis in Linear Regression, Wiley, NewYork. |
| [16] | Rousseeuw p. and Hubert M., (1997), "Recent development in PROGRESS", http://win-www.uia.ac.be/u/statis. |
| [17] | Zou H., Zhang H. (2009), "On the adaptive elastic net with a diverging number of parameters", Institute of Mathematical Statistics, Vo.37, No.4. |
| [18] | Wang, H., Li, G., Jiang, G., (2007), "Robust regression shrinkage and consistent variable selection through the LAD-Lasso", Journal of Business & Economic Statistics, Vo.25. |
| [19] | Hong, D., Zhang, F., (2010), “Weighted elastic net model for mass spectrometry imaging processing. Mathematical modeling in the medical sciences”, Vo.5, No.3. |
| [20] | Li, J.-T. , Jia, Y.-M., (2010), "An Improved Elastic Net for Cancer Classification and Gene Selection", Acta Automatica Sinica, Vo.36, No.7. |
| [21] | Wang, H., Leng, C., (2007), "Unified lasso estimation by least squares approximation", Journal of the American Statistical Association, Vo.102. |
| [22] | Pollard, D. (1991), "Asymptotics for least absolute deviation regression estimators", Econometric Theory, Vo.7 . |
| [23] | Knight' K., (1998), "Limiting Distributions for L1 Regression Estimators under General Conditions. Annals of Statistics", Vo. 26, No.2. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML