Rama Shanker
Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea
Correspondence to: Rama Shanker, Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
A new one parameter continuous distribution named “Akshaya distribution” for modeling lifetime data from biomedical science and engineering has been proposed. Its mathematical and statistical properties including its shape, moments, hazard rate function, mean residual life function, stochastic ordering, mean deviations, and Bonferroni and Lorenz curves, have been presented. The conditions under which Akshaya distribution is over-dispersed, equi-dispersed and under-dispersed are discussed along with some other one parameter lifetime distributions. The maximum likelihood estimation and the method of moments have been discussed for estimating the parameter of the proposed distribution. Finally, a numerical example of real lifetime data has been presented to test the goodness of fit of the proposed distribution and the fit has been compared with other one parameter lifetime distributions.
Keywords:
Lifetime distribution, Moments, Index of dispersion, Hazard rate function, Mean residual life function, Stochastic ordering, Mean deviations, Bonferroni and Lorenz curves, Estimation of parameter, Goodness of fit
Cite this paper: Rama Shanker, Akshaya Distribution and Its Application, American Journal of Mathematics and Statistics, Vol. 7 No. 2, 2017, pp. 51-59. doi: 10.5923/j.ajms.20170702.01.
1. Introduction
The statistical analysis and modeling of lifetime data are essential in almost all applied sciences including, biomedical science, engineering, finance, and insurance, amongst others. The classical lifetime distributions namely exponential and Lindley (1958) distributions are popular in statistics for modeling lifetime data. But these two classical lifetime distributions are not suitable from theoretical and applied point of view. Shanker et al (2015) have done a critical and comparative study regarding the modeling of lifetime data using both exponential and Lindley distributions and found that there are several lifetime data where these classical lifetime distributions are not suitable due to their shapes, hazard rate functions and mean residual life functions, amongst others. Recently, a number of one parameter lifetime distributions have been introduced by Shanker (2015 a, 2015 b, 2016 a, 2016 b, 2016 c, 2016 d, 2016 e) namely Akash, Shanker, Amarendra, Aradhana, Sujatha, Devya and Shambhu. Although these lifetime distributions give better fit than the classical exponential and Lindley distributions, there are still some lifetime data where these distributions are not suitable due to their theoretical and applied point of view. In search for a new lifetime distribution, we have proposed a new lifetime distribution which is better than Akash, Shanker, Amarendra, Aradhana, Sujatha, Devya, Shambhu, Lindley and exponential distributions for modeling lifetime data by considering a four-component mixture of an exponential 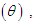 gamma
gamma 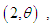 gamma
gamma 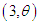 and gamma distributions with their mixing proportions
and gamma distributions with their mixing proportions 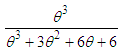 ,
, 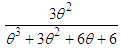 ,
, 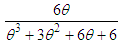 and
and 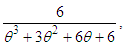 respectively. The probability density function (p.d.f.) of a new one parameter lifetime distribution can be introduced as
respectively. The probability density function (p.d.f.) of a new one parameter lifetime distribution can be introduced as 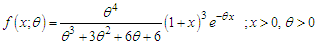 | (1.1) |
We would call this distribution, “Akshaya distribution”. The corresponding cumulative distribution function (c.d.f.) of (1.1) can be obtained as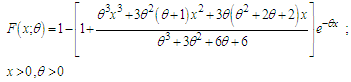 | (1.2) |
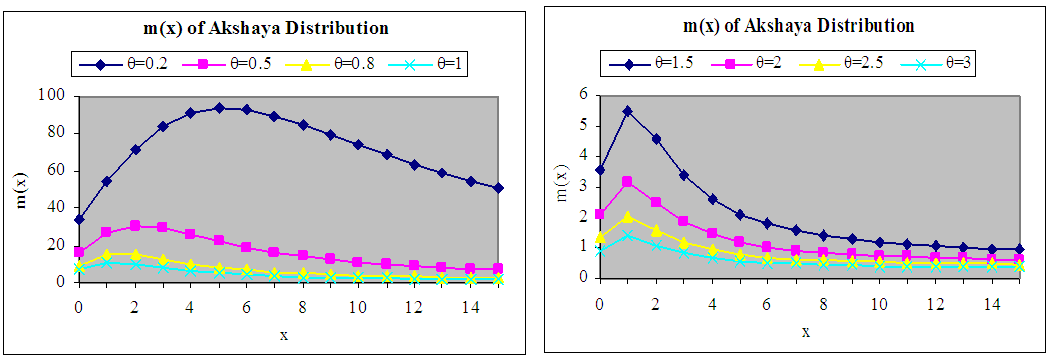
The graph of the p.d.f. and the c.d.f. of Akshaya distribution for different values of the parameter are shown in figures 1 and 2. | Figure 1. Graph of the pdf of Akshaya distribution for different values of the parameter θ |
 | Figure 2. Graph of the cdf of Akshaya distribution for different values of the parameter θ |
2. Moments and Related Measures
The moment generating function of Akshaya distribution (1.1) can be obtained as 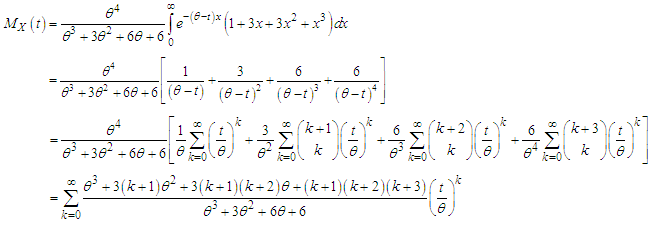 Thus the th moment about origin, as given by the coefficient of
Thus the th moment about origin, as given by the coefficient of 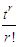 in
in 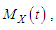 of Akshaya distributon (1.1) has been obtained as
of Akshaya distributon (1.1) has been obtained as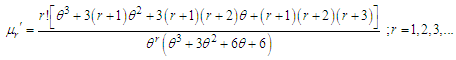 The first four moments about origin of Akshaya distribution (1.1) are obtained as
The first four moments about origin of Akshaya distribution (1.1) are obtained as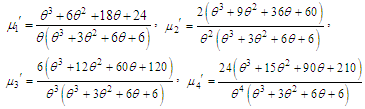 , Thus the moments about mean of the Akshaya distribution (1.1) are obtained as
, Thus the moments about mean of the Akshaya distribution (1.1) are obtained as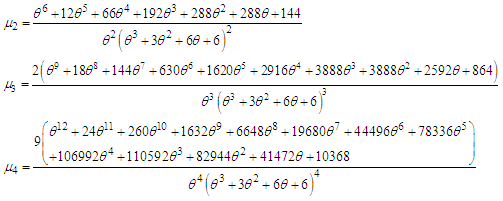 The coefficient of variation
The coefficient of variation 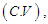 coefficient of skewness
coefficient of skewness  coefficient of kurtosis
coefficient of kurtosis 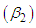 and index of dispersion
and index of dispersion 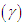 of Akshaya distribution (1.1) are thus obtained as
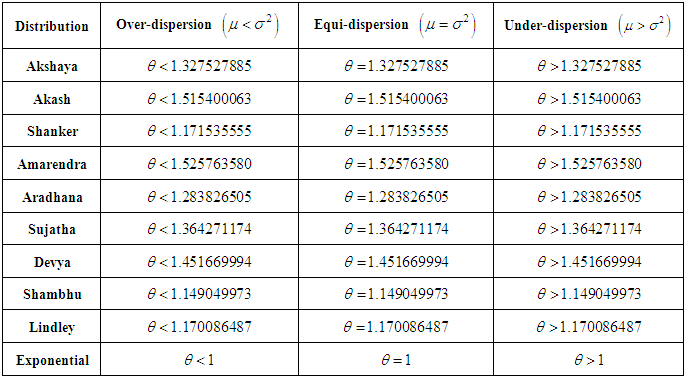
of Akshaya distribution (1.1) are thus obtained as The condition under which Akshaya distribution is over-dispersed, equi-dispersed, and under-dispersed has been studied along with condition under which Akash, Shanker, Amarendra, Aradhana, Sujatha, Devya, Shambhu, Lindley and exponential distributions are over-dispersed, equi-dispersed, and under-dispersed and are presented in table 1.
The condition under which Akshaya distribution is over-dispersed, equi-dispersed, and under-dispersed has been studied along with condition under which Akash, Shanker, Amarendra, Aradhana, Sujatha, Devya, Shambhu, Lindley and exponential distributions are over-dispersed, equi-dispersed, and under-dispersed and are presented in table 1.Table 1. Over-dispersion, equi-dispersion and under-dispersion of Akshaya, Akash, Shanker, Amarendra, Aradhana, Sujatha, Devya, Shambhu, Lindley and exponential distributions for parameter θ
 |
| |
|
3. Hazard Rate Function and Mean Residual Life Function
Let 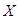 be a continuous random variable with p.d.f.
be a continuous random variable with p.d.f. 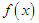 and c.d.f.
and c.d.f. 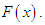 The hazard rate function (also known as the failure rate function) and the mean residual life function of
The hazard rate function (also known as the failure rate function) and the mean residual life function of 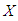 are respectively defined as
are respectively defined as 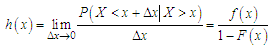 | (3.1) |
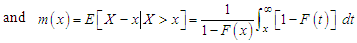 | (3.2) |
The corresponding hazard rate function, 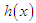 and the mean residual life function,
and the mean residual life function, 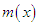 of the Akshaya distribution (1.1) are obtained as
of the Akshaya distribution (1.1) are obtained as 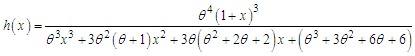 | (3.3) |
and 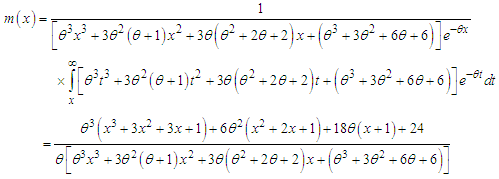 | (3.4) |
It can be easily seen that 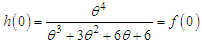 and
and 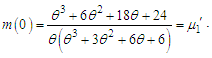 It is also obvious from the graphs of
It is also obvious from the graphs of 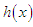 and
and 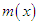 that
that 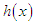 is an increasing function of
is an increasing function of 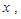 and
and 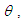 whereas
whereas 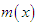 is firstly increasing and then decreasing function of
is firstly increasing and then decreasing function of 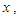 and
and 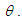 The graphs of the hazard rate function and mean residual life function of Akshaya distribution (1.1) are shown in figures 3 and 4.
The graphs of the hazard rate function and mean residual life function of Akshaya distribution (1.1) are shown in figures 3 and 4.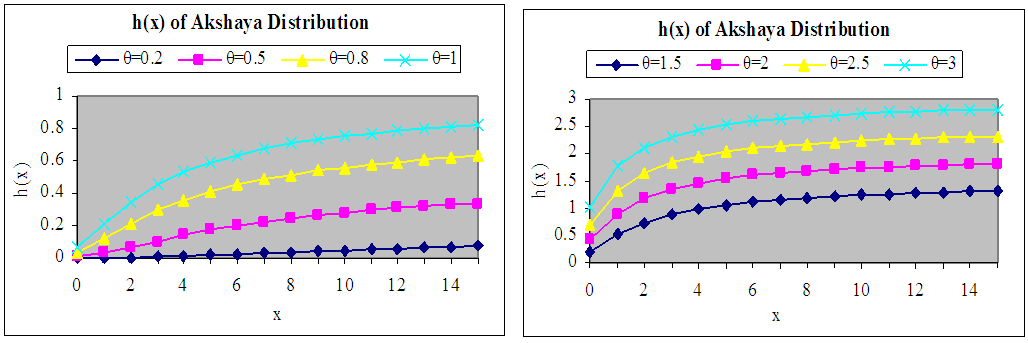 | Figure 3. Graph of hazard rate function of Akshaya distribution for varying values of parameter θ |
 | Figure 4. Graph of mean residual life function of Akshaya distribution for varying values of parameter θ |
4. Stochastic Orderings
Stochastic ordering of positive continuous random variable is an important tool for judging their comparative behavior. A random variable  is said to be smaller than a random variable
is said to be smaller than a random variable  in the (i) stochastic order
in the (i) stochastic order  if
if 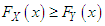 for all
for all 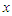 (ii) hazard rate order
(ii) hazard rate order 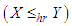 if
if 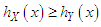 for all
for all 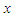 (iii) mean residual life order
(iii) mean residual life order 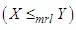 if
if 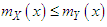 for all
for all 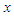 (iv) likelihood ratio order
(iv) likelihood ratio order 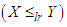 if
if 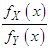 decreases in
decreases in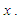 The following results due to Shaked and Shanthikumar (1994) are well known for establishing stochastic ordering of distributions
The following results due to Shaked and Shanthikumar (1994) are well known for establishing stochastic ordering of distributions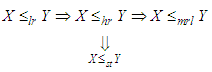 The Akshaya distribution is ordered with respect to the strongest ‘likelihood ratio’ ordering as shown in the following theorem:Theorem: Let
The Akshaya distribution is ordered with respect to the strongest ‘likelihood ratio’ ordering as shown in the following theorem:Theorem: Let 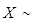 Akshaya distribution
Akshaya distribution 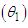 and
and 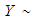 Akshaya distribution
Akshaya distribution 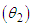 . If
. If 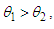 then
then 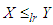 and hence
and hence 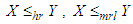 and
and 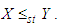 Proof: We have
Proof: We have 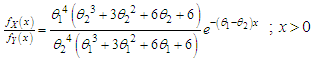 Now
Now 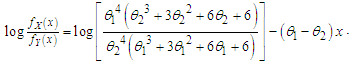 This gives
This gives 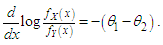 Thus for
Thus for 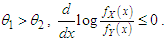 This means that
This means that 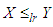 and hence
and hence 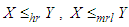 and
and 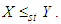
5. Mean Deviations about Mean and Median
The amount of scatter in a population is measured to some extent by the totality of deviations usually from their mean and median. These are known as the mean deviation about the mean and the mean deviation about the median and are defined as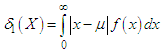 and
and 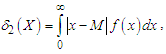 respectively, where
respectively, where 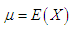 and
and 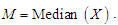 The measures
The measures 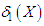 and
and 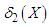 can be computed using the following simplified relationships
can be computed using the following simplified relationships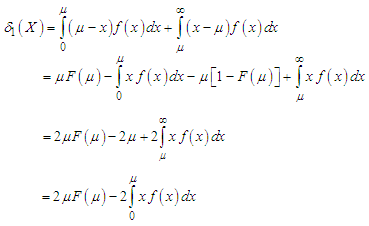 | (5.1) |
and 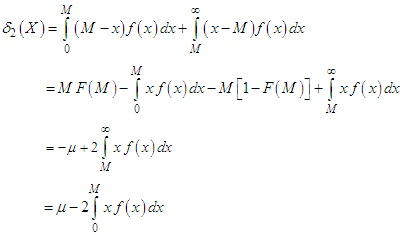 | (5.2) |
Using p.d.f. (1.1) and expression for the mean of Akshaya distribution, we get 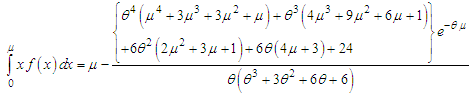 | (5.3) |
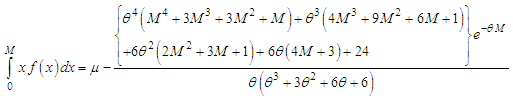 | (5.4) |
Using expressions (5.1), (5.2), (5.3) and (5.4), the mean deviation about mean 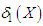 and the mean deviation about median
and the mean deviation about median 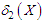 of Akshaya distribution (1.1), after a little algebraic simplification, are obtained as
of Akshaya distribution (1.1), after a little algebraic simplification, are obtained as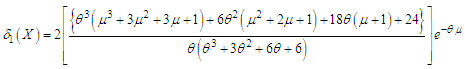 | (5.5) |
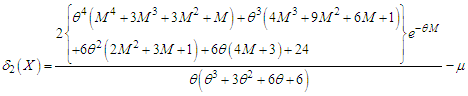 | (5.6) |
6. Bonferroni and Lorenz Curves
The Bonferroni and Lorenz curves (Bonferroni, 1930) and Bonferroni and Gini indices have applications not only in economics to study income and poverty, but also in other fields like reliability, demography, insurance and medicine. The Bonferroni and Lorenz curves are defined as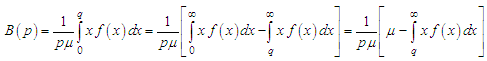 | (6.1) |
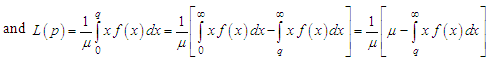 | (6.2) |
respectively or equivalently 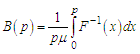 | (6.3) |
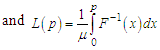 | (6.4) |
respectively, where 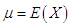 and
and 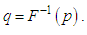 The Bonferroni and Gini indices are thus defined as
The Bonferroni and Gini indices are thus defined as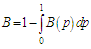 | (6.5) |
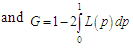 | (6.6) |
respectively.Using p.d.f. of Akshaya distribution (1.1), we get 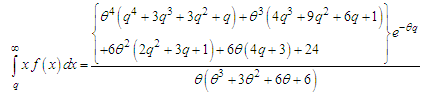 | (6.7) |
Now using equation (6.7) in (6.1) and (6.2), we get 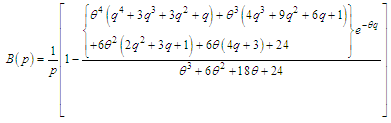 | (6.8) |
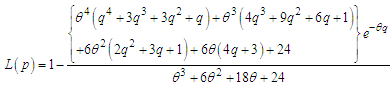 | (6.9) |
Now using equations (6.8) and (6.9) in (6.5) and (6.6), the Bonferroni and Gini indices of Akshaya distribution (1.1) are obtained as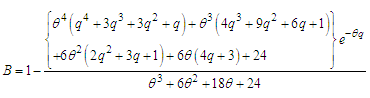 | (6.10) |
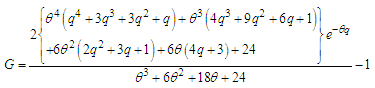 | (6.11) |
7. Estimation of Parameter
7.1. Maximum Likelihood Estimate (MLE)
Let 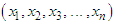 be a random sample from Akshaya distribution (1.1). The likelihood function,
be a random sample from Akshaya distribution (1.1). The likelihood function,  of Akshaya distribution is given by
of Akshaya distribution is given by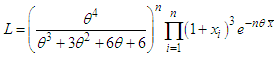 The natural log likelihood function is thus obtained as
The natural log likelihood function is thus obtained as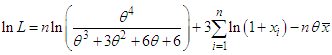 Now
Now 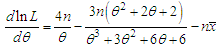 where
where 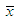 is the sample mean.The maximum likelihood estimate,
is the sample mean.The maximum likelihood estimate, 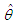 of
of 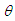 is the solution of the equation
is the solution of the equation 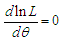 and so it can be obtained by solving the following fourth degree polynomial equation
and so it can be obtained by solving the following fourth degree polynomial equation 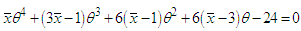 | (7.1.1) |
7.2. Method of Moment Estimate (MOME)
Equating the population mean of the Akshaya distribution to the corresponding sample mean, the MOME 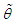 of
of 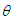 is same as given by equation (7.1.1)
is same as given by equation (7.1.1)
8. Applications and Goodness of Fit
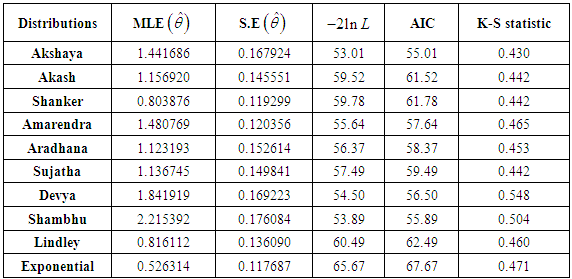
The Akshaya distribution has been fitted to a number of lifetime data set from biomedical science and engineering. In this section, we present the goodness of fit of Akshaya distribution to a real lifetime data and compare its goodness of fit with the one parameter Akash, Shanker, Amarendra, Aradhana, Sujatha, Devya, Shambhu, Lindley and exponential distributions.The data set represents the lifetime’s data relating to relief times (in minutes) of 20 patients receiving an analgesic and reported by Gross and Clark (1975, P. 105). The data are as follows:1.1, 1.4, 1.3, 1.7, 1.9, 1.8, 1.6, 2.2, 1.7, 2.7, 4.1, 1.8,1.5, 1.2, 1.4, 3.0, 1.7, 2.3, 1.6, 2.0 In order to compare lifetime distributions, 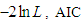 (Akaike Information Criterion) and K-S Statistics (Kolmogorov-Smirnov Statistics) for the above data set have been computed. The formulae for computing AIC and K-S Statistics are as follows:
(Akaike Information Criterion) and K-S Statistics (Kolmogorov-Smirnov Statistics) for the above data set have been computed. The formulae for computing AIC and K-S Statistics are as follows: 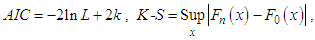 where
where 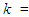 the number of parameters,
the number of parameters, 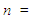 the sample size and
the sample size and 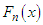 is the empirical distribution function. The best distribution is the distribution which corresponds to lower values of
is the empirical distribution function. The best distribution is the distribution which corresponds to lower values of 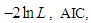 and K-S statistics. The
and K-S statistics. The 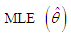 and standard error,
and standard error, 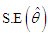 of
of 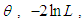 AIC and K-S Statistic of the fitted distributions are presented in the following table 2.
AIC and K-S Statistic of the fitted distributions are presented in the following table 2.Table 2.
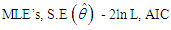 and K-S Statistics of the fitted distributions of the given data and K-S Statistics of the fitted distributions of the given data
 |
| |
|
It can be easily seen from above table that Akshaya distribution gives better fit than the fit given by Akash, Shanker, Amarendra, Aradhana, Sujatha, Devya, Shambhu, Lindley and exponential distributions and hence it can be considered as an important lifetime distribution over these lifetime distributions.
9. Conclusions
A new one parameter lifetime distribution named, “Akshaya distribution” has been suggested for modeling lifetime data from engineering and medical science. Its important mathematical and statistical properties including shape, moments, skewness, kurtosis, hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves have been discussed. The method of moments and the method of maximum likelihood estimation have also been discussed for estimating its parameter. Finally, the goodness of fit using K-S Statistics (Kolmogorov-Smirnov Statistics) for a real lifetime data have been presented to demonstrate its applicability over Akash, Shanker, Amarendra, Aradhana, Sujatha, Devya, Shambhu, Lindley and exponential distributions.
ACKNOWLEDGEMENTS
The author is grateful to the editor- in - chief and the anonymous reviewer for helpful comments which improved the quality of the paper.
References
| [1] | Bonferroni, C.E. (1930): Elementi di Statistca generale, Seeber, Firenze. |
| [2] | Gross, A.J. and Clark, V.A. (1975): Survival Distributions: Reliability Applications in the Biometrical Sciences, John Wiley, New York. |
| [3] | Lindley, D.V. (1958): Fiducial distributions and Bayes’ theorem, Journal of the Royal Statistical Society, Series B, 20, 102- 107. |
| [4] | Shaked, M. and Shanthikumar, J.G. (1994): Stochastic Orders and Their Applications, Academic Press, New York. |
| [5] | Shanker, R., Hagos, F, and Sujatha, S. (2015): On modeling of Lifetimes data using exponential and Lindley distributions, Biometrics & Biostatistics International Journal, 2 (5), 1-9. |
| [6] | Shanker, R. (2015 a): Akash distribution and its Applications, International Journal of Probability and Statistics, 4(3), 65 – 75. |
| [7] | Shanker, R. (2015 b): Shanker distribution and its Applications, International Journal of Statistics and Applications, 5(6), 338 – 348. |
| [8] | Shanker, R. (2016 a): Amarendra distribution and its Applications, American Journal of Mathematics and Statistics, 6(1), 44 – 56. |
| [9] | Shanker, R. (2016 b): Aradhana distribution and its Applications, International Journal of Statistics and Applications, 6(1), 23 – 34. |
| [10] | Shanker, R. (2016 c): Sujatha distribution and its Applications, Statistics in Transition-new series, 17(3), 1 – 20. |
| [11] | Shanker, R. (2016 d): Devya distribution and its Applications, International Journal of Statistics and Applications, 6(4), 189 – 202. |
| [12] | Shanker, R. (2016 e): Shambhu distribution and its Applications, International Journal of Probability and Statistics, 5(2), 48 -63. |


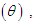 gamma
gamma  gamma
gamma 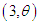 and gamma distributions with their mixing proportions
and gamma distributions with their mixing proportions 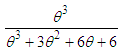 ,
, 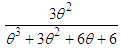 ,
, 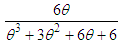 and
and 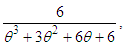 respectively. The probability density function (p.d.f.) of a new one parameter lifetime distribution can be introduced as
respectively. The probability density function (p.d.f.) of a new one parameter lifetime distribution can be introduced as 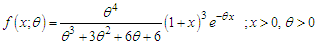
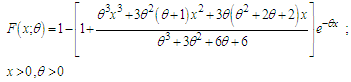


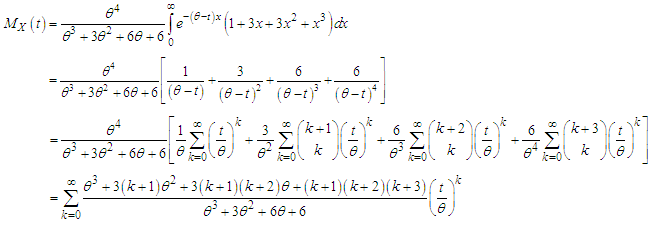 Thus the th moment about origin, as given by the coefficient of
Thus the th moment about origin, as given by the coefficient of 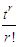 in
in 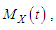 of Akshaya distributon (1.1) has been obtained as
of Akshaya distributon (1.1) has been obtained as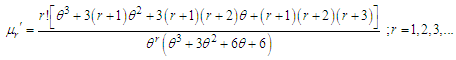 The first four moments about origin of Akshaya distribution (1.1) are obtained as
The first four moments about origin of Akshaya distribution (1.1) are obtained as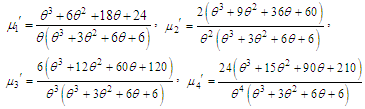 , Thus the moments about mean of the Akshaya distribution (1.1) are obtained as
, Thus the moments about mean of the Akshaya distribution (1.1) are obtained as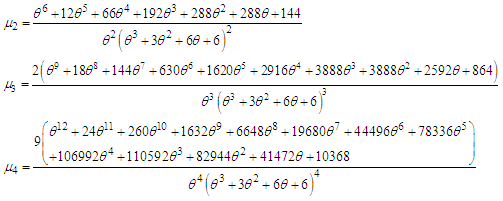 The coefficient of variation
The coefficient of variation 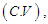 coefficient of skewness
coefficient of skewness 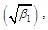 coefficient of kurtosis
coefficient of kurtosis 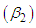 and index of dispersion
and index of dispersion 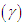 of Akshaya distribution (1.1) are thus obtained as
of Akshaya distribution (1.1) are thus obtained as The condition under which Akshaya distribution is over-dispersed, equi-dispersed, and under-dispersed has been studied along with condition under which Akash, Shanker, Amarendra, Aradhana, Sujatha, Devya, Shambhu, Lindley and exponential distributions are over-dispersed, equi-dispersed, and under-dispersed and are presented in table 1.
The condition under which Akshaya distribution is over-dispersed, equi-dispersed, and under-dispersed has been studied along with condition under which Akash, Shanker, Amarendra, Aradhana, Sujatha, Devya, Shambhu, Lindley and exponential distributions are over-dispersed, equi-dispersed, and under-dispersed and are presented in table 1.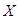 be a continuous random variable with p.d.f.
be a continuous random variable with p.d.f. 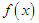 and c.d.f.
and c.d.f. 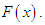 The hazard rate function (also known as the failure rate function) and the mean residual life function of
The hazard rate function (also known as the failure rate function) and the mean residual life function of 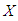 are respectively defined as
are respectively defined as 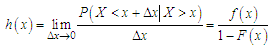
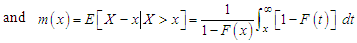
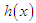 and the mean residual life function,
and the mean residual life function, 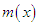 of the Akshaya distribution (1.1) are obtained as
of the Akshaya distribution (1.1) are obtained as 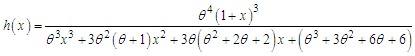
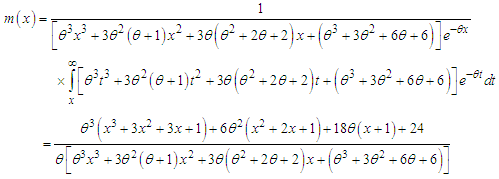
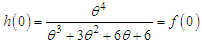 and
and 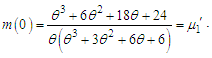 It is also obvious from the graphs of
It is also obvious from the graphs of  and
and  that
that  is an increasing function of
is an increasing function of 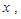 and
and 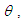 whereas
whereas 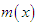 is firstly increasing and then decreasing function of
is firstly increasing and then decreasing function of 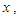 and
and 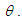 The graphs of the hazard rate function and mean residual life function of Akshaya distribution (1.1) are shown in figures 3 and 4.
The graphs of the hazard rate function and mean residual life function of Akshaya distribution (1.1) are shown in figures 3 and 4.

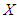 is said to be smaller than a random variable
is said to be smaller than a random variable 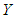 in the (i) stochastic order
in the (i) stochastic order 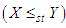 if
if 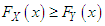 for all
for all 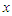 (ii) hazard rate order
(ii) hazard rate order 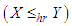 if
if 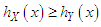 for all
for all 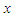 (iii) mean residual life order
(iii) mean residual life order 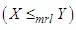 if
if 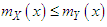 for all
for all 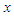 (iv) likelihood ratio order
(iv) likelihood ratio order 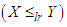 if
if 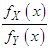 decreases in
decreases in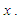 The following results due to Shaked and Shanthikumar (1994) are well known for establishing stochastic ordering of distributions
The following results due to Shaked and Shanthikumar (1994) are well known for establishing stochastic ordering of distributions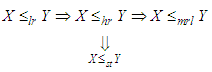 The Akshaya distribution is ordered with respect to the strongest ‘likelihood ratio’ ordering as shown in the following theorem:Theorem: Let
The Akshaya distribution is ordered with respect to the strongest ‘likelihood ratio’ ordering as shown in the following theorem:Theorem: Let 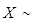 Akshaya distribution
Akshaya distribution 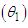 and
and 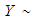 Akshaya distribution
Akshaya distribution 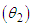 . If
. If 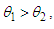 then
then 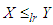 and hence
and hence 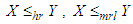 and
and 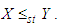 Proof: We have
Proof: We have 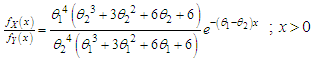 Now
Now 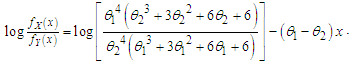 This gives
This gives 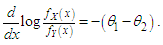 Thus for
Thus for 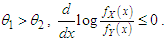 This means that
This means that 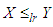 and hence
and hence 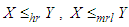 and
and 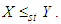
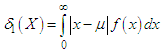 and
and 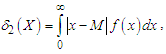 respectively, where
respectively, where  and
and  The measures
The measures  and
and 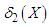 can be computed using the following simplified relationships
can be computed using the following simplified relationships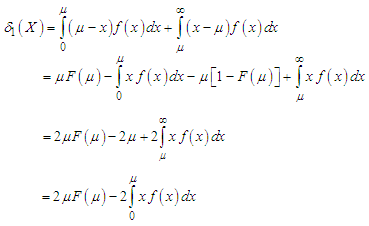
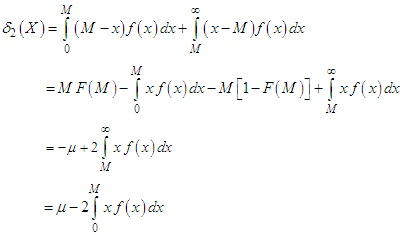
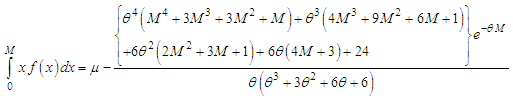
 and the mean deviation about median
and the mean deviation about median  of Akshaya distribution (1.1), after a little algebraic simplification, are obtained as
of Akshaya distribution (1.1), after a little algebraic simplification, are obtained as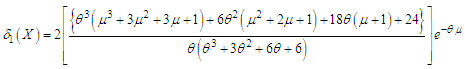
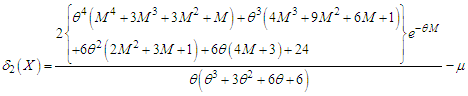
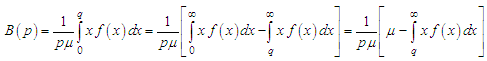
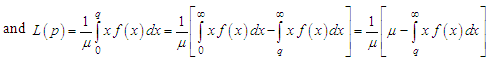
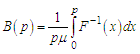
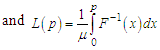
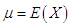 and
and 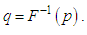 The Bonferroni and Gini indices are thus defined as
The Bonferroni and Gini indices are thus defined as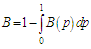
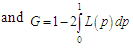
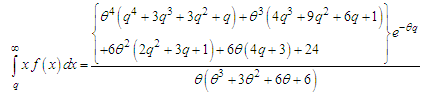
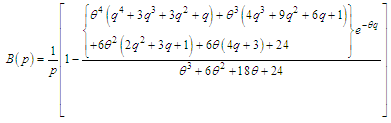
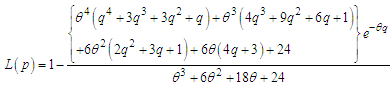
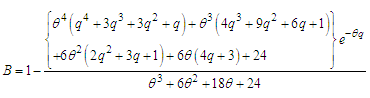
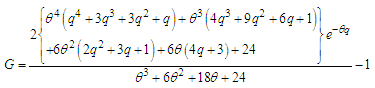
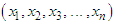 be a random sample from Akshaya distribution (1.1). The likelihood function,
be a random sample from Akshaya distribution (1.1). The likelihood function,  of Akshaya distribution is given by
of Akshaya distribution is given by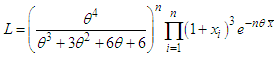 The natural log likelihood function is thus obtained as
The natural log likelihood function is thus obtained as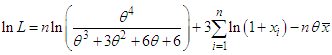 Now
Now 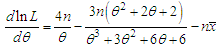 where
where  is the sample mean.The maximum likelihood estimate,
is the sample mean.The maximum likelihood estimate, 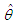 of
of 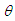 is the solution of the equation
is the solution of the equation 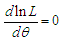 and so it can be obtained by solving the following fourth degree polynomial equation
and so it can be obtained by solving the following fourth degree polynomial equation 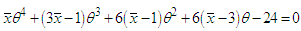
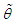 of
of 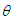 is same as given by equation (7.1.1)
is same as given by equation (7.1.1) 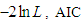 (Akaike Information Criterion) and K-S Statistics (Kolmogorov-Smirnov Statistics) for the above data set have been computed. The formulae for computing AIC and K-S Statistics are as follows:
(Akaike Information Criterion) and K-S Statistics (Kolmogorov-Smirnov Statistics) for the above data set have been computed. The formulae for computing AIC and K-S Statistics are as follows: 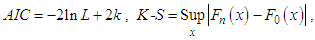 where
where 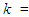 the number of parameters,
the number of parameters, 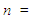 the sample size and
the sample size and 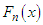 is the empirical distribution function. The best distribution is the distribution which corresponds to lower values of
is the empirical distribution function. The best distribution is the distribution which corresponds to lower values of 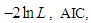 and K-S statistics. The
and K-S statistics. The 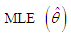 and standard error,
and standard error, 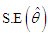 of
of 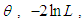 AIC and K-S Statistic of the fitted distributions are presented in the following table 2.
AIC and K-S Statistic of the fitted distributions are presented in the following table 2. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
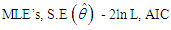 and K-S Statistics of the fitted distributions of the given data
and K-S Statistics of the fitted distributions of the given data