-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2017; 7(1): 38-43
doi:10.5923/j.ajms.20170701.06

Conharmonically Flat Vaisman-Gray Manifold
Habeeb M. Abood, Yasir A. Abdulameer
Department of Mathematics, College of Education for Pure Sciences, Basra University, Basra, Iraq
Correspondence to: Habeeb M. Abood, Department of Mathematics, College of Education for Pure Sciences, Basra University, Basra, Iraq.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper is devoted to study some geometrical properties of conharmonic curvature tensor of Vaisman-Gray manifold. In particular, we have found the necessary and sufficient condition that flat conharmonic Vaisman-Gray manifold is an Einstein manifold.
Keywords: Almost Hermitian Manifold, Vaisman-Gray manifold, Conharmonic tensor
Cite this paper: Habeeb M. Abood, Yasir A. Abdulameer, Conharmonically Flat Vaisman-Gray Manifold, American Journal of Mathematics and Statistics, Vol. 7 No. 1, 2017, pp. 38-43. doi: 10.5923/j.ajms.20170701.06.
1. Introduction
- One of the representative work of differential geometry is an almost Hermitian structure. Gray and Hervalla [1] found that the action of the unitary group
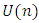 on the space of all tensors of type (3,0) decomposed this space into sixteen classes. The conditions that determined each one of these classes belongs to the type of almost Hermitian structure have been identified. These conditions were formulated by using the method of Kozel's operator [2]. The Russian researcher Kirichenko found an interesting method to study the different classes of almost Hermitian manifold. This method depending on the space of the principal fiber bundle of all complex frames of manifold
on the space of all tensors of type (3,0) decomposed this space into sixteen classes. The conditions that determined each one of these classes belongs to the type of almost Hermitian structure have been identified. These conditions were formulated by using the method of Kozel's operator [2]. The Russian researcher Kirichenko found an interesting method to study the different classes of almost Hermitian manifold. This method depending on the space of the principal fiber bundle of all complex frames of manifold 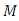 with structure group is the unitary group
with structure group is the unitary group 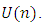 This space is called an adjoined
This space is called an adjoined 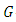 -structure space, more details about this space can be found in [3-6].One of the most important classes of almost Hermitian structures is denoted by
-structure space, more details about this space can be found in [3-6].One of the most important classes of almost Hermitian structures is denoted by 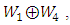 where
where 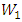 and
and 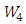 respectively denoted to the nearly
respectively denoted to the nearly 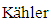 manifold and local conformal
manifold and local conformal 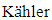 manifold.A harmonic function is a function whose Laplacian vanishes. Related to this fact, Y. Ishi [7] has studied conharmonic transformation which is a conformal transformation that preserves the harmonicity of a certain function. Agaoka, et al. [8] studied the twisted product manifold with vanishing conharmonic curvature tensor. Agaoka, et al. [9] studied the fibred Riemannian space with flat conharmonic curvature tensor, in particular, they proved that a conharmonically flat manifold is locally the product manifold of two spaces of constant curvature tensor with constant scalar curvatures. Siddiqui and Ahsan [10] gave an interesting application when they studied the conharmonic curvature tensor on the four dimensional space-time that satisfy the Einstein field equations. Abood and Lafta [11] studied the conharmonic curvature tensor of nearly
manifold.A harmonic function is a function whose Laplacian vanishes. Related to this fact, Y. Ishi [7] has studied conharmonic transformation which is a conformal transformation that preserves the harmonicity of a certain function. Agaoka, et al. [8] studied the twisted product manifold with vanishing conharmonic curvature tensor. Agaoka, et al. [9] studied the fibred Riemannian space with flat conharmonic curvature tensor, in particular, they proved that a conharmonically flat manifold is locally the product manifold of two spaces of constant curvature tensor with constant scalar curvatures. Siddiqui and Ahsan [10] gave an interesting application when they studied the conharmonic curvature tensor on the four dimensional space-time that satisfy the Einstein field equations. Abood and Lafta [11] studied the conharmonic curvature tensor of nearly 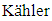 and almost
and almost 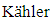 manifolds. The present work devoted to study the flatness of conharmonic curvature tensor of Vaisman-Gray manifold by using the methodology of an adjoined
manifolds. The present work devoted to study the flatness of conharmonic curvature tensor of Vaisman-Gray manifold by using the methodology of an adjoined 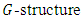 space.
space.2. Preliminaries
- Suppose that
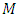 is
is 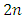 -dimensional smooth manifold,
-dimensional smooth manifold, 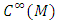 is a set of all smooth functions on
is a set of all smooth functions on 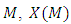 is the module of smooth vector fields on
is the module of smooth vector fields on 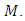 An almost Hermitian manifold
An almost Hermitian manifold 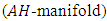 is the set
is the set 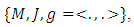 where
where 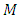 is a smooth manifold, and
is a smooth manifold, and 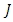 is an almost complex structure, and
is an almost complex structure, and 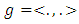 is a Riemannian metric, such that
is a Riemannian metric, such that 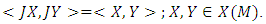 Suppose that
Suppose that 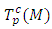 is the complexification of tangent space
is the complexification of tangent space 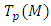 at the point
at the point 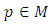 and
and 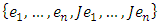 is a real adapted basis of
is a real adapted basis of 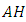 -manifold. Then in the module
-manifold. Then in the module 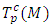 there exists a basis given by
there exists a basis given by 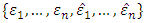 which is called adapted basis, where,
which is called adapted basis, where, 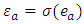 and
and 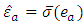 and
and 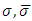 are two endomorphisms in the module
are two endomorphisms in the module 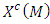 which are defined by
which are defined by 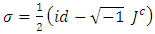 and
and 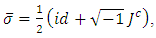 such that,
such that, 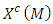 and
and 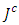 are the complexifications of
are the complexifications of 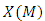 and
and 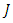 respectively. The corresponding frame of this basis is
respectively. The corresponding frame of this basis is 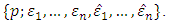 Suppose that the indexes
Suppose that the indexes 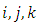 and
and 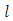 are in the range
are in the range  and the indexes
and the indexes 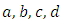 and
and 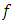 are in the range
are in the range 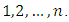 And
And 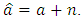 The
The 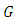 -structure space is the principal fiber bundle of all complex frames of manifold
-structure space is the principal fiber bundle of all complex frames of manifold 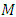 with structure group is the unitary group
with structure group is the unitary group 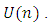 This space is called an adjoined
This space is called an adjoined 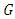 -structure space.In the adjoined
-structure space.In the adjoined 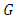 -structure space, the components matrices of complex structure
-structure space, the components matrices of complex structure 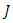 and Riemannian metric
and Riemannian metric 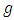 are given by the following:
are given by the following: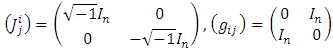 | (2.1) |
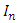 is the identity matrix of order
is the identity matrix of order 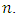 Definition 2.1 [12] The Riemannian curvature tensor
Definition 2.1 [12] The Riemannian curvature tensor 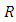 of a smooth manifold
of a smooth manifold 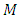 is an 4-covariant tensor
is an 4-covariant tensor 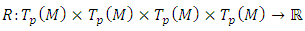 which is defined by:
which is defined by: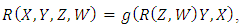 where
where 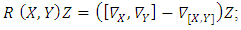
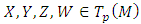 and satisfies the following properties:
and satisfies the following properties: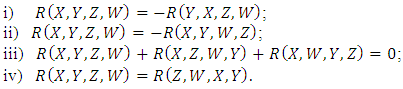 Definition 2.2 [13] The Ricci tensor is a tensor of type (2,0) which is defined as follows:
Definition 2.2 [13] The Ricci tensor is a tensor of type (2,0) which is defined as follows: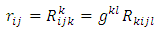 Definition 2.3 [7] The conharmonic tensor of an
Definition 2.3 [7] The conharmonic tensor of an  -manifold is a tensor
-manifold is a tensor  of type (4,0) which is defined as the form:
of type (4,0) which is defined as the form: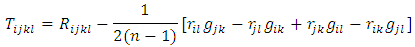 where
where 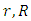 and
and 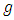 are respectively Ricci tensor, Riemannian curvature tensor and Riemannian metric. Similar to the properties of Riemannian curvature tensor, the conharmonic tensor has the following properties:
are respectively Ricci tensor, Riemannian curvature tensor and Riemannian metric. Similar to the properties of Riemannian curvature tensor, the conharmonic tensor has the following properties: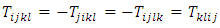 Definition 2.4. An
Definition 2.4. An 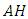 -manifold is called a conharmonically flat if the conharmonic tensor vanishes.Definition 2.5 [14] In the adjoined
-manifold is called a conharmonically flat if the conharmonic tensor vanishes.Definition 2.5 [14] In the adjoined 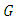 -structure space, an
-structure space, an 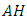 -manifold
-manifold 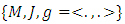 is called a Vaisman-Gray manifold
is called a Vaisman-Gray manifold 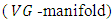 if
if 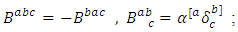 is called a locally conformal
is called a locally conformal 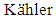 manifold
manifold 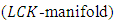 if
if 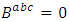 and
and 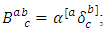 and is called a nearly
and is called a nearly  manifold
manifold  if
if 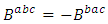 and
and 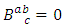 , where
, where 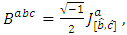
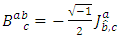 and
and 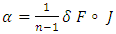 is a Lie form;
is a Lie form; 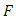 is a
is a 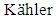 form which is defined by
form which is defined by 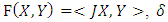 is a coderivative and
is a coderivative and 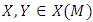 and the bracket [ ] denote to the antisymmetric operation.Theorem 2.6 [15] In the adjoined
and the bracket [ ] denote to the antisymmetric operation.Theorem 2.6 [15] In the adjoined 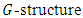 space, the components of Riemannian curvature tensor of
space, the components of Riemannian curvature tensor of 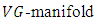 are given by the following forms:
are given by the following forms: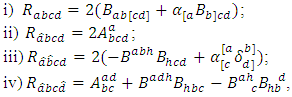 where,
where, 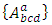 are some functions on adjoined
are some functions on adjoined 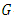 - structure space and
- structure space and 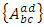 are system of fuctions in the adjoined
are system of fuctions in the adjoined 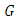 -structure space which are symmetric by the lower and upper indices which are called components of holomorphic sectional curvature tensor.and
-structure space which are symmetric by the lower and upper indices which are called components of holomorphic sectional curvature tensor.and 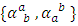 are the components of the covariant differential structure tensor of first and second type and
are the components of the covariant differential structure tensor of first and second type and 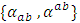 are the components of the Lee form on adjoint
are the components of the Lee form on adjoint  -structure space such that:
-structure space such that: 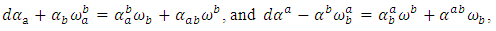 where,
where, 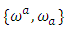 are the components of mixture form,
are the components of mixture form, 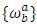 are the components of Riema-nnian connection of metric
are the components of Riema-nnian connection of metric 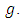 The other components of Riemannian curvature tensor
The other components of Riemannian curvature tensor 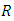 can be obtained by the property of symmetry for
can be obtained by the property of symmetry for 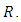 There are three special classes of almost Hermitian manifold depending on the components of the Riemannian curvature tensor. Their conditions are embodied in the following definition:Definition 2.7. [16] In the adjoined
There are three special classes of almost Hermitian manifold depending on the components of the Riemannian curvature tensor. Their conditions are embodied in the following definition:Definition 2.7. [16] In the adjoined 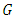 -structure space, an
-structure space, an 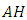 -manifold is a manifold of class:1)
-manifold is a manifold of class:1) 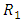 if and only if,
if and only if, 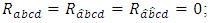 2)
2) 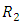 if and only if,
if and only if, 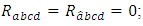 3)
3) 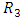
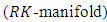 if and only if,
if and only if, 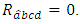 It easy to see that
It easy to see that 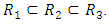 Theorem 2.8 [15] In the adjoined
Theorem 2.8 [15] In the adjoined 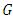 -structure space, the components of Ricci tensor of
-structure space, the components of Ricci tensor of 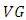 -manifold are given by the following forms:
-manifold are given by the following forms: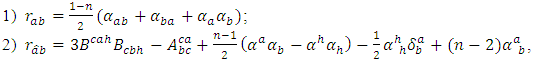 and the others are conjugate to the above components. Definition 2.9 [17] A Riemannian manifold is called an Einstein manifold, if the Ricci tensor satisfies the equation
and the others are conjugate to the above components. Definition 2.9 [17] A Riemannian manifold is called an Einstein manifold, if the Ricci tensor satisfies the equation 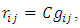 where,
where, 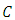 is an Einstein constant.Definition 2.10 [18] An
is an Einstein constant.Definition 2.10 [18] An 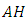 -manifold has
-manifold has 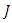 -invariant Ricci tensor, if
-invariant Ricci tensor, if 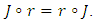 The following Lemma gives a fact about Ricci tensor in the adjoined
The following Lemma gives a fact about Ricci tensor in the adjoined 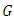 -structure space.Lemma 2.11 [16] An
-structure space.Lemma 2.11 [16] An 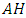 -manifold has
-manifold has 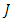 -invariant Ricci tensor if and only if, we have
-invariant Ricci tensor if and only if, we have 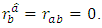 Definition 2.12 [3] Define two endomorphisms on
Definition 2.12 [3] Define two endomorphisms on 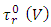 as follows:i) Symmetric mapping Sym:
as follows:i) Symmetric mapping Sym: 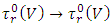 by:
by: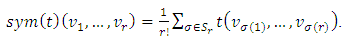 ii) Antisymmetric mapping Alt:
ii) Antisymmetric mapping Alt: 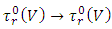 by:
by: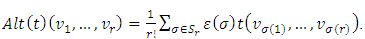 The symbols ( ) and [ ] are usually used to denote the symmetric and antisymmetric respectively.
The symbols ( ) and [ ] are usually used to denote the symmetric and antisymmetric respectively. 3. Main Results
- Theorem 3.1. In the adjoined
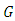 -structure space, the components of conharmonic tensor of
-structure space, the components of conharmonic tensor of 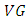 -manifold are given by the following forms:
-manifold are given by the following forms: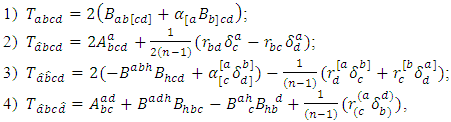 and the others are conjugate to the above components.Proof:1) Put
and the others are conjugate to the above components.Proof:1) Put 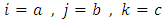 and
and 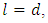 we have
we have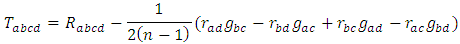 According to the equation (2.1) we deduce that
According to the equation (2.1) we deduce that 2) Put
2) Put 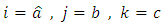 and
and 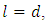 we get
we get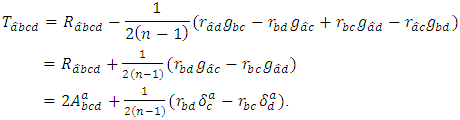 3) Put
3) Put 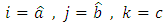 and
and 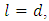 it follows that
it follows that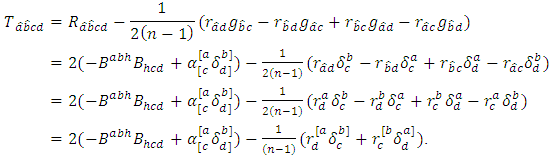 4) Put
4) Put 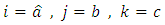 and
and 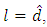 we obtain
we obtain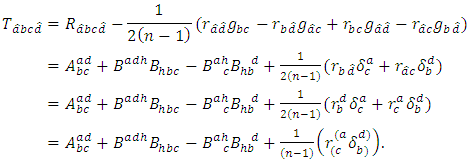 Definition 3.2. In the adjoined
Definition 3.2. In the adjoined  -structure space, an almost Hermitian manifold is a manifold of class:
-structure space, an almost Hermitian manifold is a manifold of class: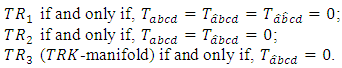 We call
We call 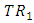 a conharmonic para
a conharmonic para  manifold.Theorem 3.3. Let
manifold.Theorem 3.3. Let  be a
be a 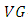 -manifold of class
-manifold of class 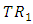 with
with 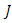 -invariant Ricci tensor, then
-invariant Ricci tensor, then 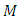 is a manifold of class
is a manifold of class 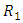 if and only if,
if and only if, 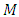 is a manifold of flat Ricci tensor.Proof:To prove
is a manifold of flat Ricci tensor.Proof:To prove 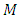 is a manifold of class
is a manifold of class 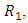 we must prove that
we must prove that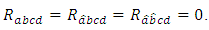 Let
Let 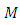 be a manifold of class
be a manifold of class 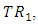 according to definition 3.2, we have
according to definition 3.2, we have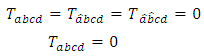 | (3.1) |
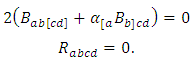 | (3.2) |
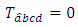 According to theorems 2.6 and 3.1, we deduce
According to theorems 2.6 and 3.1, we deduce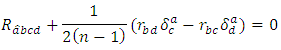 Since,
Since, 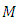 has
has 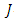 -invariant Ricci tensor, then
-invariant Ricci tensor, then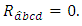 | (3.3) |
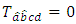 By using theorems 2.6 and 3.1, we have
By using theorems 2.6 and 3.1, we have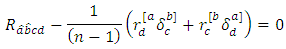 Suppose that
Suppose that 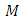 is a manifold of flat Ricci tensor, then
is a manifold of flat Ricci tensor, then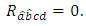 | (3.4) |
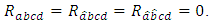 Conversely, by using the equation (3.1), we have
Conversely, by using the equation (3.1), we have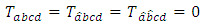 By using theorem 3.1, it follows that
By using theorem 3.1, it follows that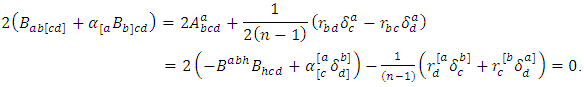 Let
Let 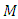 be a manifold of class
be a manifold of class 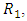 then, according to theorem 2.6 and definition 2.7, we obtain
then, according to theorem 2.6 and definition 2.7, we obtain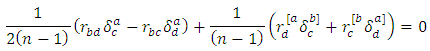 Symmetrizing by the indexes
Symmetrizing by the indexes 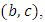 we get
we get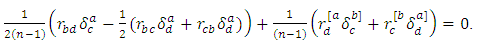 Antisymmetrizing by the indexes
Antisymmetrizing by the indexes 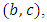 we have
we have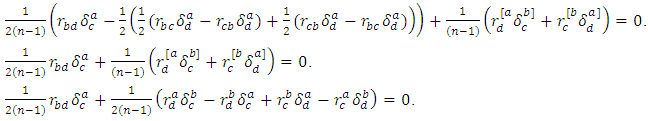 Symmetrizing by the indexes
Symmetrizing by the indexes 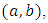 we deduce
we deduce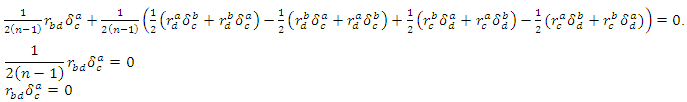 Contracting by the indexes
Contracting by the indexes 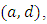 we have
we have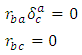 Since
Since 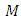 has
has 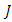 -invariant Ricci tensor, then
-invariant Ricci tensor, then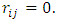 Theorem 3.4. Suppose that
Theorem 3.4. Suppose that 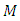 is
is 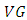 -manifold of class
-manifold of class 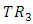 with
with 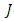 -invariant Ricci tensor, then
-invariant Ricci tensor, then 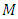 is a manifold of class
is a manifold of class 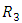 if and only if,
if and only if, 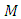 is a manifold of flat Ricci tensor.Proof:Suppose that
is a manifold of flat Ricci tensor.Proof:Suppose that 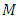 is a manifold of class
is a manifold of class 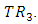 According to definition 3.2., we have
According to definition 3.2., we have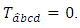 By using the Theorem 3.1, we deduce
By using the Theorem 3.1, we deduce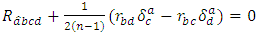 | (3.5) |
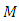 be a manifold of class
be a manifold of class 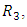 then
then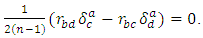 Symmetrizing by the indexes
Symmetrizing by the indexes 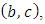 we get
we get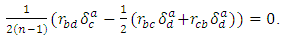 Antisymmetrizing by the indexes
Antisymmetrizing by the indexes 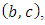 we have
we have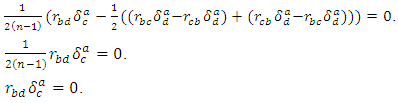 Contracting by the indexes
Contracting by the indexes 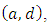 it follows that
it follows that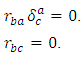 Since
Since  has
has 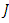 -invariant Ricci tensor, then
-invariant Ricci tensor, then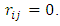 Conversely, by using the equation (3.5), we have
Conversely, by using the equation (3.5), we have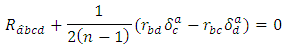 Suppose that
Suppose that 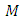 is a manifold of flat Ricci tensor, then
is a manifold of flat Ricci tensor, then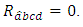 Therefore,
Therefore,  is a manifold of class
is a manifold of class  The following theorem gives the necessary and sufficient condition in which an
The following theorem gives the necessary and sufficient condition in which an 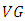 -manifold is an Einstein manifold. Theorem 3.5. Suppose that
-manifold is an Einstein manifold. Theorem 3.5. Suppose that 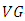 is conharmonically flat
is conharmonically flat  -manifold with
-manifold with 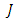 -invariant Ricci tenor. Then the necessary and sufficient condition that
-invariant Ricci tenor. Then the necessary and sufficient condition that 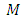 an Einstein manifold, is
an Einstein manifold, is 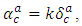 where
where 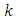 is a constant.Proof:Let
is a constant.Proof:Let 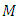 be a conharmonically flat
be a conharmonically flat 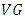 -manifold. According to the definition 2.4 and theorem 3.1, we have
-manifold. According to the definition 2.4 and theorem 3.1, we have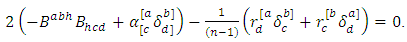 Contracting by the indexes
Contracting by the indexes 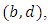 it follows that
it follows that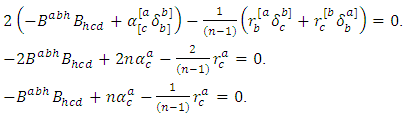 Symmetrizing by the indexes
Symmetrizing by the indexes 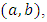 we deduce
we deduce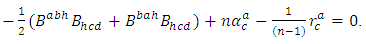 Antisymmetrizing by the indexes
Antisymmetrizing by the indexes 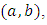 it follows that
it follows that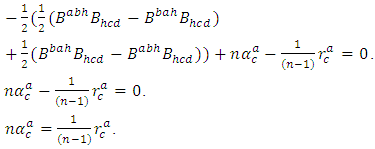 | (3.6) |
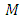 be an Einstein manifold, then
be an Einstein manifold, then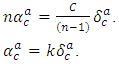 Conversely, by using the equation (3.6), we have
Conversely, by using the equation (3.6), we have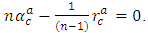 Since,
Since, 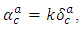 we deduce
we deduce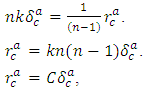 where,
where, 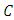 represent an Einstein constant.Since
represent an Einstein constant.Since 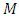 has
has 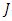 -invariant Ricci tensor. Therefore,
-invariant Ricci tensor. Therefore, 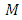 is an Einstein manifold.
is an Einstein manifold.4. Conclusions
- The present work is devoted to study the flatness of conharmonic curvature tensor of Vaisman-Gray manifold. We found out an interesting application in theoretical physics. In particular, we found the necessary and sufficient condition that a conharmonically flat Vaisman-Gray manifold is an Einstein manifold.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML