1. Introduction

A regular polygon is any geometric plane figure bound by three or more equal straight lines and possessing equal internal angles [1, 2]. Plane figures as the equilateral triangles, squares, pentagons, hexagons etc are the lower families. The constructions of regular polygons demands special methods because the majority of their respective base (or external) angles are not readily achieved by ordinary construction and bisection of angles. Even with the introduction of equipartition of plane angles [3], most of the angles of the polygons with many sides are tedious to construct because the base angles get larger and close as the number of sides increase.

Currently there are many procedures for constructing regular polygons. Each method usually is for a family. Any regular polygon can be constructed using its base (or external) angle; this is the age long procedure and it is hampered by the difficulty in constructing some of these base or external angles. Other methods via use of advanced mathematical calculations have been applied in the construction of the odd number sided regular polygons such as the pentagon (5-gon) and heptadecagon (17-gon) [4]. A list of novel procedures for the lower families from equilateral triangle (trigon) to regular nonagon (9-gon) are also available [5].

Most of the established procedures construct regular polygons whose sides are to be measured [6, 7], but a number of the methods construct regular polygons of predetermined side lengths [5].

As mentioned above, majority of the methods of constructing regular polygons are tailored to particular family. A regular polygon family consists of regular polygons that differ in side lengths only. A question arises whether there can be a general method that is applicable to the construction of any of the polygon family? The answer is yes because there is a method describing the construction of regular polygons on same base [6] which is termed the “two triangle rule”. This assumes that regular polygons drawn on a common base with their centres lying on the perpendicular bisector of the common base have their centres equally separated. This constant distance (separation) between neighboring centres when added to the centre of any regular polygon along the perpendicular bisector gives the centre for the next regular polygon.

For the benefit of the reader, the constant distance between centres is obtained by drawing one of the congruent isosceles triangles of a 4-gon (congruent isosceles triangles of a regular polygon have their common apex at the centre of the polygon figure 1; an equilateral triangle is a special isosceles triangle) and that of a 6-gon on a common base AB, figure 2. The bisection of ac (a is the apical point of triangle aAB and also the centre of 4-gon and c the apex of triangle cAB and also the centre of 6-gon) gives point b the apex of triangle bAB and also the centre of 5-gon. The addition of the length ab or bc to c gives point d the centre of a regular 7-gon. Other polygon centres can be obtained by adding appropriate integers of ab or bc to a chosen centre.

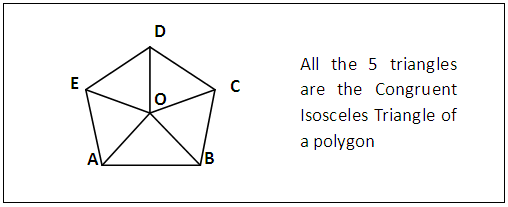Figure 1. Illustration of Congruent Isosceles Triangle of a polygon with a Regular Pentagon

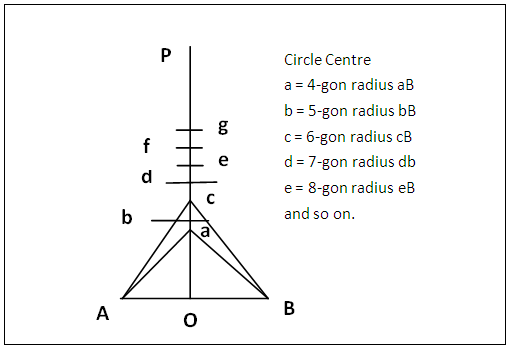Figure 2. The “two-triangle rule” general method for constructing regular Polygons

There is no proof to this assumption except that the method gives the expected result. However the method suggests that it is possible to generate a general method for the construction of any regular polygon of predetermined side length. There is therefore the need to seek for a general method with mathematical support for the construction of any regular polygon of predetermined side length. This paper presents this general method that constructs any regular polygon starting from a square (a regular polygon) of same side as the regular polygon.

2. Methodology

In the descriptions that follow, a circle with centre O and radius OA is denoted as circle O of radius OA. Any polygon here after mentioned is a regular polygon.

2.1. Constructing any Regular Polygon from a Given Square BRST

(a). Draw the square BRST and let the diagonals intersect at O, figure 3. Produce RB upwards.

(b). Elsewhere mark out the distance OB (half the distance of the diagonal of the square) as TY on a straight line and tetrasect it into TU = UV = VX = XY. On RB produced, from B as centre and with radius TU mark equal intercepts BC = CD = DE = EF = FG = GH = HI = IJ and so on to the polygon of interest as indicated in figure 3 under ‘Radius’.

(c). To construct a pentagon for example, figure 4, a circle of radius OC (OC from figure 3) is drawn and its circumference partitioned with radius BR (the side of the given square) to give ABCDE as the pentagon, figure 4.

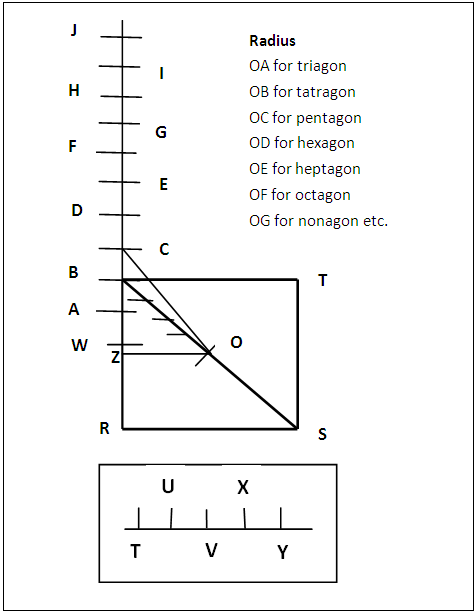Figure 3. Constructing any Polygon through a Square: determination of radius of each circle

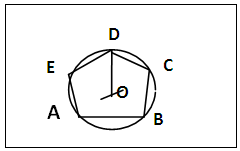Figure 4. 5-gon by Square Method

2.2. The Case of the Triagon

From figure 3, the addition of TU (one quarter of OB) starts from point B the point for tetragon upwards. If this quarter of OB is marked from B down, point A is obtained. The circumference of circle O of radius OA sectored with BR (the side of the square) gives a triagon.

2.3. What Figure is Obtained for Point W that is one Quarter of OB (i.e. TU) below A?

Circle O of radius OW sectored with BR gives a straight line (the diameter of that particular circle), figure 3.

2.4. Application of the Square Method of Polygon Construction in the Construction of any Regular Polygon Angle (Illustrated with the Base Angle of a Heptagon)

This method can be used to construct any base/external angle of a regular polygon as follows.

(a) Construct a square ABCD of choice producing the side BA upwards, figure 5. Determine the midpoint O of its diagonal and tetrasect OA into OG = GH = HJ = JA. Draw the perpendicular bisector EF of the sides AB and CD producing both ways.

(b). Centre A and radius AG cut BA produced at K, K is heptagon centre. Join KO. ∠KOE is half the base angle of a 7-gon.

(c). At point O on EF and on the side KO transfer ∠KOE by the routine method to get ∠LOE which is twice ∠KOE and is the required heptagon base angle. Automatically ∠LOF is the external angle of the heptagon.

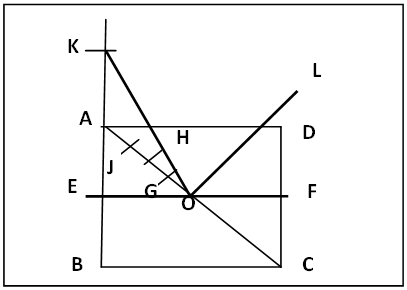Figure 5. Polygon Base Angle Construction illustrated with that of heptagon

2.5. Inscribing any Polygon in a Given Circle

While a circle can circumscribe any given regular polygon, not all polygons can be inscribed in a given circle. A few can be inscribed directly in a given circle as shown below, others require the application of other methods.

2.5.1. Inscribing a Regular Polygon e.g. 3- and 6-gon in a Given Circle using the Radius of the Given Circle

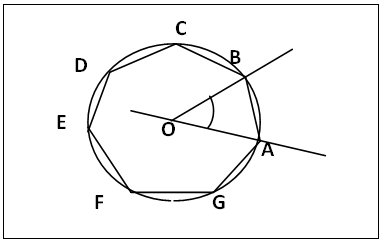
(a). Draw the given circle O with radius OA, figure 6.

(b). Starting from point A, with radius OA cut the circumference of the circle equally at B, C, D, E and F. (c)(i). For a regular 3-gon, join AC, CE and EA as the 3-gon (dotted lines) inscribed in the given circle. (ii). For 6-gon, join points AB, BC, CD, DE, EF and FA to obtain the 6-gon inscribed in the given circle.

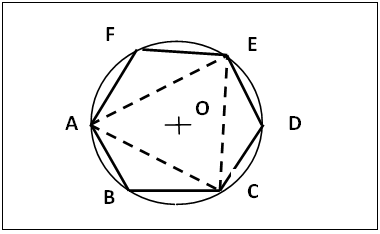Figure 6. Inscribing a 3- and a 6-gon in a Circle

2.5.2. Inscribing a Regular Polygon e.g. 4- and 8-gon in a Given Circle using the External Angle of the Polygon if it is Easily Obtained by Construction

(a). Draw the given circle O with centre O and radius OA, figure 7. Draw four diameters AE, BF, CG and DH of the circle inclined to one another at 45°.

(b). For a regular 4-gon, join AC, CE, EG and GA to get regular 4-gon (dotted lines) inscribed in the given circle. For a regular 8-gon, join AB, BC, CD, DE, EF, FG, GH and HA to get regular 8-gon inscribed in the given circle.

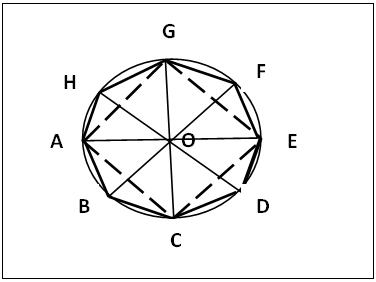Figure 7. Inscribing a 4- and 8-gon in a given Circle

2.5.3. Application of the Square Method of Polygon Construction in Inscribing any Polygon (7-gon say) in a Given Circle

(a). Draw a square ABCD of choice, figure 8a, and tetrasect half the diagonal OD into OP = PQ = QR = RD. Produce AD upwards. Centre D and with appropriate integral units of quarter of DO that correspond to the polygon (DP for heptagon, see figure 8a) as radius cut AD produced at E say for heptagon.

(b). Centre O and radius OE draw the inner circle O, figure 8b. Equally sector this circle into seven with the square side AB as radius and producing the radial lines OP, OQ, OR, OS, OT, OU, OU and OV outwards, figure 8(b).

(c). Centre O and radius that of the given circle swing the given circle that cuts the radial lines at A, B, C, D, E, F and G. Join these points to form the inscribed polygon (heptagon) in the given circle, the outer circle.

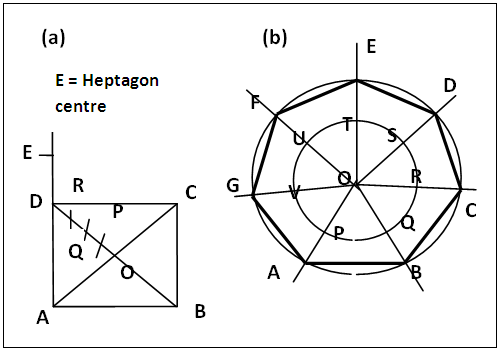Figure 8. IIIustrating Inscription of a Polygon in a given Circle applying the Square Method of constructing Polygons

Alternatively

(a). Draw the given circle, elsewhere construct the base angle of the polygon family, section 2.4. figure 5, and copy the external angle LOF figure 5 to the centre of the given circle as ∠AOB figure 9.

(b). Partition the circumference of the circle with radius AB into AB = BC = CD = DE= EF = FG = GA, figure 9. Join the points to get the inscribed polygon (heptagon in this case) ABCDEFG.

Figure 9. Use of external Angle via Square Method in inscribing a polygon in a given Circle

3. Result and Discussion

3.1. The Two-Triangle Rule

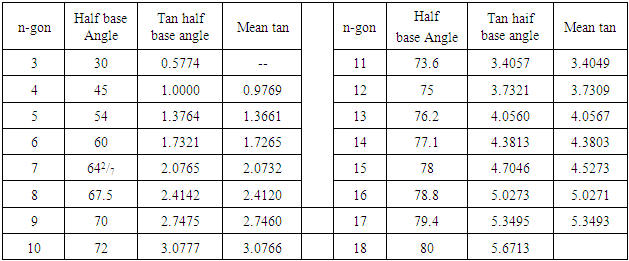
The Two-Triangle rule [6] used the respective congruent triangles of 4- and 6-gons with their respective apexes as the respective polygon centres to derive the required increment, figure 2, by constructing a right angled isosceles triangle AaB (with apex a) and an equilateral triangle AcB with apex c. The midpoint b of ac is the centre of a regular 5-gon and ab = bc is the required increment. Hence c + ab = d and d + ab = e and so on. The basis for this could be that as tanƟ is opposite side divided by the adjacent side in general, with constant base (adjacent side), the tangent of an angle varies directly as the opposite side. Therefore, the length of opposite side will be directly proportional to the tangent of the half base angle of neighboring polygons and the difference in length will be constant.

Again the isosceles triangles of each polygon have their respective apical points at the respective centres of the 4-gon and 6-gon. The base angles of each isosceles triangle are respectively half the base angle of the respective polygon. That is ∠aAB is half the base angle of a 4-gon and ∠cAB is half the base angle of a 6-gon, figure 2. Taking the tangents of the half base angles of regular polygons at constant adjacent side showed that the tangents of the half base angle of any of the polygons is the mean of those of its immediate neighbors, see Table 1. From this observation, if x, y and z respectively stand for the tangents of half base angles of three direct polygon neighbors with increasing number of side, it means that y = (x + z)/2 or 2y = x + z. Hence y – x = z – y. This shows that at constant base the centres of regular polygons are of same distance apart, this is a second proof of the two triangle rule.

Table 1. Tangents of half Base Angles (°) of some regular Polygons

3.2. Polygon Construction via the Square

This procedure emanated from an article in which a regular octagon was development from a given square [5].

In that article [5], the distance OB (i.e. half the diagonal of the square) added to point B on RB produced as in figure 3 generated a regular octagon. That is point F in figure 3 generated a regular octagon. An attempt to know what figure is generated by adding another intercept of OB to point F opened up this general method, because when this was made, point J for a regular dodecagon (12-gon) was obtained. Further addition of OB to point J gave point N (not indicated) for a regular hexadecagon (16-gon). It then means that the addition of OB to point B on the produced side of the square will generate the fourth higher member of regular polygon from the point of addition and the addition of a quarter of OB will give the regular polygon next to the polygon generated by that point of addition. Referring to figure 3, addition of a quarter of OB gives point C. Point C is the centre for regular pentagon. Thus this general method of constructing any regular polygon via the use of a square of same side length emerged. This method uses a square to generate regular polygons of same side as the square. This new method does not need to construct any angle of any of the polygons for its operation except 90° which is needed in the construction of the generating square. This reduces errors and is an added advantage.

3.3. Angle Construction by the Square Method

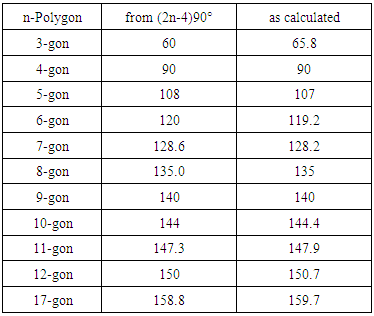
As the centre of any regular polygon can be easily located by the square method, and half the isosceles triangle of the regular polygon drawn, the base angle of any regular polygon can be constructed. by merely drawing the appropriate square, tetrasecting half of its diagonal (or dividing the diagonal into eight equal parts) and adding up the appropriate quarters of OB to point B, figure 3 to obtain the point along RB produced that gives the centre of the polygon. This centre joined to the midpoint of the diagonal and midpoint of the appropriate side of the square give half the base angle of the polygon. So one needs only to draw the square with its diagonal and not the “grid” in figure 3 in order to construct the base angle of any regular polygon. As an example, figure 5, to construct the base angle of a regular heptagon (7-gon), half base angle is constructed and doubled. That is tanEOK = EK/EO. But EK = EA + AK, EO = EA = a/2 and AK = 3(a√2)/8 where a is the side of the square. Hence tanEOK = [a/2 + 3(a√2)/8]/a/2 = 1 + 0.75√2 = 2.0607. Angle EOK = 64.1° Base angle of heptagon is 2(64.1°) = 128.2°, compare with 128.6° in table 2. By similar calculations other base angles of some regular polygons are obtained as displayed in the Table 2. Therefore regular polygon construction by the use of a square opens up an easy way for constructing any angle of a regular polygon (excepting regular triagon). The use of the square method in constructing angles of regular polygons confirms and stands as a typical example of an earlier statement [5] that there exists other methods of constructing the angles of regular polygons not yet explored. This method also provides a third proof for the “two triangle rule” since the centres of the polygons are of equal intercepts along the perpendicular bisector of the common base.

Table 2. Base Angles of regular Polygons

3.4. Inscribing any Polygon in a Given Circle

Inscribing a regular polygon in a given circle is possible when the side of the regular polygon is equal to the radius of the circle or is derivable from the radius. This is the case with 3- and 6-gons. Also if the external angle of the polygon is readily derived by construction (here multiple bisection) of the angle of revolution at the centre of the circle, the polygon is easily inscribed as in the case of in 4- and 8-gons.

In section 2.5.3, figure 8a, the application of the square method for constructing regular polygons in the inscription of a polygon in a given circle is like enlarging or shrinking a working polygon to the required size. The working polygon is first constructed by the square method and is then enlarged or shrunk to be inscribed in a given circle.

The alternative route, figure 8b is possible because the external angle of any regular polygon can now be easily constructed (as shown in section 2.4, figure 5).

The difficulty in inscribing a polygon in a given circle is that only one member of a family with particular side length will fit in the given circle. The determination of this particular member is provided by each of these two procedures. The alternative method that uses the external angle inscribes the required polygon directly in the given circle bypassing the use of an intermediate working polygon.

3.5. Similarity/Difference of the “Two Triangle Rule” to this Square Method

Both procedures use the isosceles triangle formed by joining the ends of the base of each regular polygon to the centre of the polygon to construct the polygon. This is an adaptation of the age-old method. As the polygons have a common base, their centres will lie on the perpendicular bisector of the common base. For each polygon, the centre of the circumscribing circle will be at the centre of each polygon and is located along the perpendicular bisector of the common side. The radius of each respective circle is the straight line from the respective polygon centre to the edge of the common side.

The difference in the two methods is that the two triangle rule constructs the square and the hexagon to obtain the increment to be added while the square method uses only the square and works out the increment (distance between polygon centers along the perpendicular bisector of the common base) as a quarter of half the diagonal of the square in use. The square method constructs the exact half base angle of any regular polygon with no averaging. Also the square method is easy to manipulate and has more applications than the two triangle rule.

3.6. The case of the Triagon in the two Methods and Point W (figure 3) in the Square Method

Though the triagon can be constructed by any of the two methods, the mean of the tangents of half base angles of 3-gon and 5-gon in table 2 gives the value for 4-gon only to one decimal place. In the square method, the calculation of half the base angle of a 3-gon as detailed in section 3.3 does not give the expected result, Table 2. There is no ready explanation to any of these discrepancies or observations.

The addition of a quarter of OB to point A down ward, figure 3, gave point W. Circle O with radius OW sectored with BR gave the diameter of that same circle which shows that there is no other polygon below triagon in the polygon series.

4. Conclusions

The square method of constructing regular polygons offers a general procedure for constructing any regular polygon by using a square of same side as the regular polygon. This method not only proved that on a common base, the centres of neighboring regular polygons differ by a constant distance, thus strengthening the two triangle rule, it also confirmed an earlier statement [5] that the square (and the equilateral triangle) play important role in the construction of regular polygons. This square method offers a convenient procedure for constructing the base/external angle of any regular polygon. Some other angles above 90 can also be constructed by joining the midpoint of any neighboring points along RB produced to point O, figure 3, and their values calculated. The application of the square method of constructing regular polygons makes it possible to inscribe any regular polygon in a given circle. Again the square method proves that the triagon is the first polygon in the series of regular polygons. These are welcome developments.