Fagbamigbe AF, Adebowale AS, Bamgboye EA
Department of Epidemiology and Medical Statistics, Faculty of Public Health, College of Medicine, University of Ibadan, Ibadan, Nigeria
Correspondence to: Fagbamigbe AF, Department of Epidemiology and Medical Statistics, Faculty of Public Health, College of Medicine, University of Ibadan, Ibadan, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Bivariate censored data occur in follow-up studies of events that can result in two different outcomes. Many studies have explored methods for inference about the marginal recurrence times of these outcomes. However, very few have focused on the dependence structures between their occurrences or recurrence times especially when these outcomes are censored as evidence in the current study. This theoretical and empirical study used simulated data to monitor and validate the survival analysis model for measuring association between recurrence times of bivariate censored outcomes. Bivariate outcomes would naturally fall into one of four possibilities: only the first, only the second, none or both conditions occurring with different and distinct likelihoods. Using predetermined correlation coefficients, n=100000 bivariate standardized binormal data were simulated. The simulated data were then subjected to different censoring chances while contributions of the likelihoods of the four possibilities were examined and Maximum Likelihood Estimate (MLE) of the association parameter determined. For the data simulated at 50% censoring, MLE of the association parameter tended to zero as the predetermined correlation coefficients fell from +1.0 to -1.0. However, at 0% censoring, the MLE were approximates of the predetermined correlation coefficients. The developed model was robust as the model responded adequately to the dynamics of the predetermined correlation and censoring conditions. The model would be appropriate in studying associations between two censored survival times.
Keywords:
Bivariate Censored outcomes, Maximum likelihood estimates, Censoring, Simulation
Cite this paper: Fagbamigbe AF, Adebowale AS, Bamgboye EA, A Survival Analysis Model for Measuring Association between Bivariate Censored Outcomes: Validation Using Mathematical Simulation, American Journal of Mathematics and Statistics, Vol. 7 No. 1, 2017, pp. 7-14. doi: 10.5923/j.ajms.20170701.02.
1. Introduction
Bivariate censored data arise in the study of a phenomenon with two possible outcomes in which the time before occurrence or recurrence of the event of interest may be the same or differ in the two outcomes [1]. Literature is replete on studies involving such phenomenon. Amongst are the diabetic retinopathy study [2], the Australian twins study [3], the Danish twin register [4] and a ventilation tube study for otitis media patients [5]. Sometimes, it is of interest to determine the possible associations between the times of occurrence of these events especially if both were subjected to censoring. Although, previous studies in bivariate survival analysis have focused mainly on methods for inference about the marginal survival times, very few have investigated dependence structures between bivariate outcomes [6-10]. Our objective is to validate a model for determining the dependence structure of the timing of the bivariate outcomes of interest with the view of providing insight into whether occurrence of one of the outcomes depends on the other or not.In some biomedical applications of survival analysis techniques, researchers are often interested in the dependence relationship between the lifetimes of two variables in an individual. For example, the analysis of data on lifetimes of twins has been used by geneticists as a tool for assessing genetic effect on mortality [11]. Also, in the studies of HIV/AIDS, the dependence between the time from HIV infection to full blown AIDS and the time from full blown AIDS to death may reveal useful information about the evolution of the disease process.The study of associations among bivariate and multivariate outcomes becomes a necessity in scientific research because dependence between two random variables is completely described by their bivariate distribution. The well-known standard methods could be used to make inferences when a bivariate distribution has a simple form but constraints usually surface when the form is a bit complex. However, based on some standardized assumptions, one may alternatively create bivariate distributions thereby restricting the use of the standard methods [12-16]. These limitations occur very often when working with bivariate discrete distributions and in most cases they allow only for positive dependence or must have marginal distributions of a given form [17].Researches in multivariate survival analysis had largely concentrated on non-parametric estimation of the survival functions [8, 9, 18]. Deviation from the multivariate survival analysis is the estimation of bivariate survival function which has information about the dependence structure. However, there have been constraints on this bivariate analysis because the dependence structure is hard to visualize due to the discreteness nature of the developed method of estimating the survival functions till date [16].The study on the estimation of Kendal’s τ under censoring showed that censoring is a common phenomenon in analysis of lifetime data and it is essential that estimates of τ be available for bivariate censored data [19]. However, few results for this fundamental problem have appeared in literature. Several estimators of  under censoring have been proposed [12, 13, 20, 21], but none of the estimators is consistent when the true value of τ is not equal to zero, that is, when the marginal(s) are dependent [14]. The bias of these estimators increases as the degree of dependence increases. They had expressed τ as an integral of the bivariate survival function. Adopting the ideas presented in an early study, [22], a natural way to estimate
under censoring have been proposed [12, 13, 20, 21], but none of the estimators is consistent when the true value of τ is not equal to zero, that is, when the marginal(s) are dependent [14]. The bias of these estimators increases as the degree of dependence increases. They had expressed τ as an integral of the bivariate survival function. Adopting the ideas presented in an early study, [22], a natural way to estimate 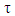 is to plug a suitable bivariate survival estimator into the integral form that defines
is to plug a suitable bivariate survival estimator into the integral form that defines  [19].Interval censoring was used in a previous study that assessed the association between bivariate current status data [23] rather than right censoring used in our study. Wang and colleague proposed a method for measuring correlations in the presence of interval censored data. The Wang et al approach was adopted in the study of characterization of the correlation between ages at entry into Breast and Pubic Hair development among teenagers [24]. Interval censoring occurs in a survival data situation when its univariate setting is considered and one is interested in a fatigue time variable T which is never observed, but can only be determined to lie below or above a random monitoring or censoring time C; where C and T are assumed to be independent [25]. The use of conditional Kendall’s τ for estimating association among bivariate interval censored data has been proposed in a recent study [14]. Similarly, Lakhal et al developed an IPCW estimator for Kendall’s
[19].Interval censoring was used in a previous study that assessed the association between bivariate current status data [23] rather than right censoring used in our study. Wang and colleague proposed a method for measuring correlations in the presence of interval censored data. The Wang et al approach was adopted in the study of characterization of the correlation between ages at entry into Breast and Pubic Hair development among teenagers [24]. Interval censoring occurs in a survival data situation when its univariate setting is considered and one is interested in a fatigue time variable T which is never observed, but can only be determined to lie below or above a random monitoring or censoring time C; where C and T are assumed to be independent [25]. The use of conditional Kendall’s τ for estimating association among bivariate interval censored data has been proposed in a recent study [14]. Similarly, Lakhal et al developed an IPCW estimator for Kendall’s 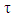 under bivariate censoring [13]. Until now, copula models are main methods used in estimating association between bivariate censored data [26] but there has been criticism against the method. Arkady et al observed that the approach is elegant and may be effective, but added that the methods sometimes prove to be insufficient depending on the type of association between the paired observations [27]. The source of this insufficiency, apparently, is the problem of dimensionality, where a two-variate survival function
under bivariate censoring [13]. Until now, copula models are main methods used in estimating association between bivariate censored data [26] but there has been criticism against the method. Arkady et al observed that the approach is elegant and may be effective, but added that the methods sometimes prove to be insufficient depending on the type of association between the paired observations [27]. The source of this insufficiency, apparently, is the problem of dimensionality, where a two-variate survival function 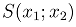 was used in order to model the behavior of three-variate joint first-life and last-survivor functions. The over reliance of copula models on Bayesian techniques by using prior distributions at the second stage in copula models makes the method difficult to use. Hence, the development of the parametric modelling of association between bivariate censored outcomes by Fagbamigbe et al [28]. The parametric model was a simpler model than the copula models and it relied less on Bayesian techniques. The study developed an alternative model for determining existence and measuring association between bivariate censored outcomes. The study illustrated the application of the model using censored outcomes of recurrences of kidney infections among people with kidney failure in North England. The authors of the study found that positive and significant associations existed between recurrence times in kidney infection and was optimized at +0.2868 [28].The present study is primarily aimed at monitoring the procedures of the model
was used in order to model the behavior of three-variate joint first-life and last-survivor functions. The over reliance of copula models on Bayesian techniques by using prior distributions at the second stage in copula models makes the method difficult to use. Hence, the development of the parametric modelling of association between bivariate censored outcomes by Fagbamigbe et al [28]. The parametric model was a simpler model than the copula models and it relied less on Bayesian techniques. The study developed an alternative model for determining existence and measuring association between bivariate censored outcomes. The study illustrated the application of the model using censored outcomes of recurrences of kidney infections among people with kidney failure in North England. The authors of the study found that positive and significant associations existed between recurrence times in kidney infection and was optimized at +0.2868 [28].The present study is primarily aimed at monitoring the procedures of the model 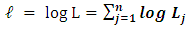 which was earlier developed to determine the possible associations between bivariate outcome using data generated via statistical simulations and to highlight dimensions that were not addressed in our previous study. Unlike the previous study that applied a real lifetime data to the method the current study used simulated that under certain conditions. Our major focus was validation of the procedures of the model using a set of predetermined correlation coefficients at 0% censoring (when all events are presumed to be observed) and 50% censoring (when all events have equal chances of being served or not).
which was earlier developed to determine the possible associations between bivariate outcome using data generated via statistical simulations and to highlight dimensions that were not addressed in our previous study. Unlike the previous study that applied a real lifetime data to the method the current study used simulated that under certain conditions. Our major focus was validation of the procedures of the model using a set of predetermined correlation coefficients at 0% censoring (when all events are presumed to be observed) and 50% censoring (when all events have equal chances of being served or not).
2. Methods
2.1. The Model
Literature suggested that in bivariate survival analysis, two outcomes (observations) occur in any follow up study [6, 23, 28]. A particular case or individual followed over time may have neither of the two events of interest, (a good outcome), one or the other, or both (a bad outcome). The likelihoods corresponding to the four different categories are expressed individually as H1(x, y) which involves a situation when the two outcomes, say X and Y are both observed during the follow up. However, the survival (observational) time of the two outcomes may not be the same. Let H2(x,y) denote the likelihood of the situation where the first lifetime is observed (X) and second lifetime (Y) is censored at C2, while H3(x,y) denote the likelihood of the situation where the first lifetime (X) is censored at C1and second lifetime (Y) is observed. H4(x,y) denotes the fourth possible situation whereby neither of the events of interest took place but the survival time was rather censored, so let H4(x, y) denote the likelihood of the situation where the two lifetimes X and Y are censored at C1 and C2 respectively. The censoring time C1 and C2 may or may not be the same.Such that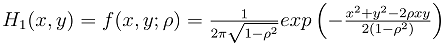 | (1) |
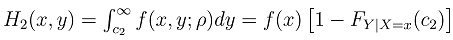 | (2) |
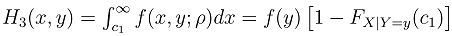 | (3) |
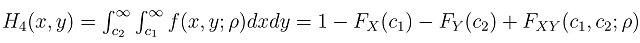 | (4) |
where,C1= the censoring time for the first outcomeC2= the censoring time for the second outcomeFX (c1) is the normal cumulative distribution function of X at c1Fy (c2) is the normal cumulative distribution function of Y at c2FX|Y=y(c1) is the marginal distribution function of X at c1 given YFY|X=x(c2) is the marginal distribution function of Y at c2 given XFX,Y(c1,c2;ρ) is the bivariate cumulative distribution function of X and Y at c1 and c2 respectively with correlation ρ.We then used normal multivariate distribution estimators (pnorm, dnorm, pnorm, pmvnorm and dmvnorm) in R-statistical software to integrate and determine the necessary functions following the principle for likelihood estimation. The choice of normalization at this stage is due to its robustness and it has been used earlier in similar process [15, 24].Adapted from reports of Betensky et al [15], Christensen et al [24] used maximum likelihood approach to estimate the correlation between ages at occurrence of two distinct observed events, with modifications to accommodate the interval censored nature of the available data. Betensky et al had applied multiple implementation technique on the estimated bivariate distribution so as to replace the set of undefined bivariate failure times [15]. We adapted the methodology as well but with modifications to suit right censored data. Considering a pair of event times, defined as X for the first event and Y for the second, they have a joint probability density distribution  . The corresponding cumulative distribution function of the paired variables,
. The corresponding cumulative distribution function of the paired variables, 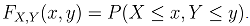 If X and Y follow a bivariate normal distribution,
If X and Y follow a bivariate normal distribution, 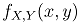 takes the form in equation 5.
takes the form in equation 5.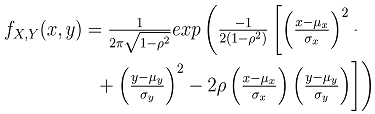 | (5) |
whereas  could be expressed as
could be expressed as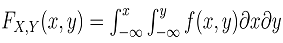 | (6) |
The resulting likelihood for the four possible scenarios is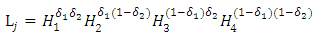 | (7) |
where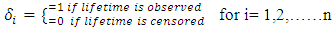 | (8) |
n is number of observationsThen, the logarithm of 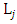 gives
gives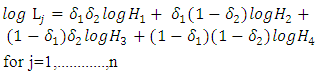 | (9) |
where n is number of observationsThen, the overall likelihood model to be maximized is thus 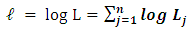 | (10) |
Previous studies [14, 15, 19, 29] have used similar procedures. Further documentation can be found in an earlier study [28].
2.2. Simulation Study
We carried out a simulation study so as to assess the performance of the suggested estimator in a finite sample. Using R statistical software, we simulated sets of n=100,000 standardized binormal random variables -(x, y) ~ mvn(0, 1; 0, 1) as a proxy for normalized failure times with a set of predetermined correlation coefficients (ρ) from -1.0 to +1.0 where mvn is a package in the statistical software for simulating multivariate random variable with a specified mean (in this case “0”) and standard deviation (in this case “1”). A recent study has explored several methods of normalizing a censored bivariate data [16]. Each simulated data were in turn assigned to two different censoring conditions. Under the first condition, each bivariate simulated data was randomly assigned censoring index with equal chances (50%) so that each has either index “1” or “0” for “observed” or “censored” observations respectively. However, under the second condition (0% censoring chances), none of the data in the two marginals of the simulated data were censored, that is they were all assigned “0” censoring index. Under this condition, we assumed that all events were observed. We then applied the simulated data with their respective censoring index to the model  in equations 10 to obtain the Maximum Likelihood Estimation (MLE) of association parameter for each of the simulated bivariate data under the two conditions been considered. To ensure the reliability and validity of the simulated failure time data, we computed its theoretical correlation coefficient using Pearson’s product moment correlation methods. Hessian matrix was used in computing the standard error of the maximum likelihood estimations. The idea of simulation is very intuitive and has been used in literature and also in a recent study to estimate conditional Kendall’s tau for bivariate interval censored data. The study considered two different censoring levels: high right and moderate right censoring rates and set τ = 0.0; 0.3; 0.5; 0.7 where, τ = 0 implies the pairs of events are not dependent [14].
in equations 10 to obtain the Maximum Likelihood Estimation (MLE) of association parameter for each of the simulated bivariate data under the two conditions been considered. To ensure the reliability and validity of the simulated failure time data, we computed its theoretical correlation coefficient using Pearson’s product moment correlation methods. Hessian matrix was used in computing the standard error of the maximum likelihood estimations. The idea of simulation is very intuitive and has been used in literature and also in a recent study to estimate conditional Kendall’s tau for bivariate interval censored data. The study considered two different censoring levels: high right and moderate right censoring rates and set τ = 0.0; 0.3; 0.5; 0.7 where, τ = 0 implies the pairs of events are not dependent [14].
3. Results
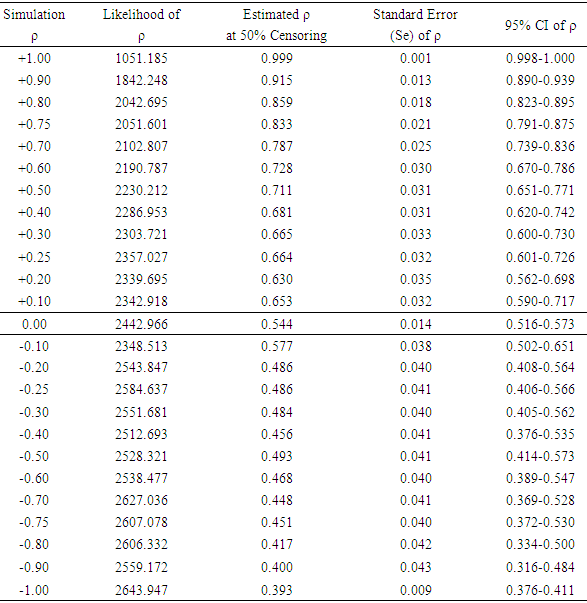
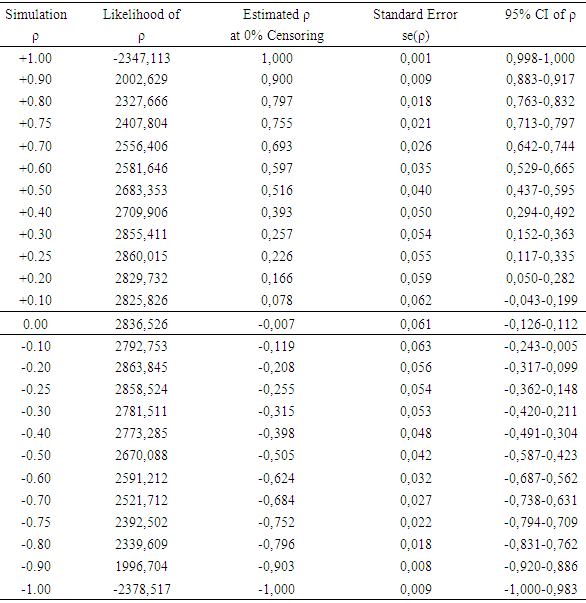
At 50% censoring, the bivariate data simulated using predetermined correlation coefficient of 1.00, has maximum likelihood of 1051.185 and maximized correlation estimate of 0.999. At predetermined correlation coefficients of 0.5, 0.0, -0.5 and -1.00; the maximum likelihood and the estimate of the association were (2230.212 and 0.711), (2442.966 and 0.544), (2528.321 and 0.493) and (2643.947 and 0.393) respectively. The standard errors of the estimated ρ were lower at the tails of the predefined correlation coefficients than around the zero.With 0% censoring, the simulated bivariate censored data had a maximum likelihood of -2347.113 which produced an estimate (ρ) of 0.999 for the association parameter. At predetermined correlation coefficients of 0.5, 0.0, -0.5 and 1.00, the maximum likelihoods and the estimated association parameters were (2683.353 and 0.516), (2836.526 and -0.007), (2591.212 -0.505) and (2670.088 and -0.999) respectively as shown in Table 2 and Figure 1.Table 1. Estimated association parameters of bivariate simulated data under different predetermined correlation coefficient at 50% censoring
 |
| |
|
Table 2. Estimated association parameters of bivariate simulated data under different predetermined correlation coefficient at 0% censoring
 |
| |
|
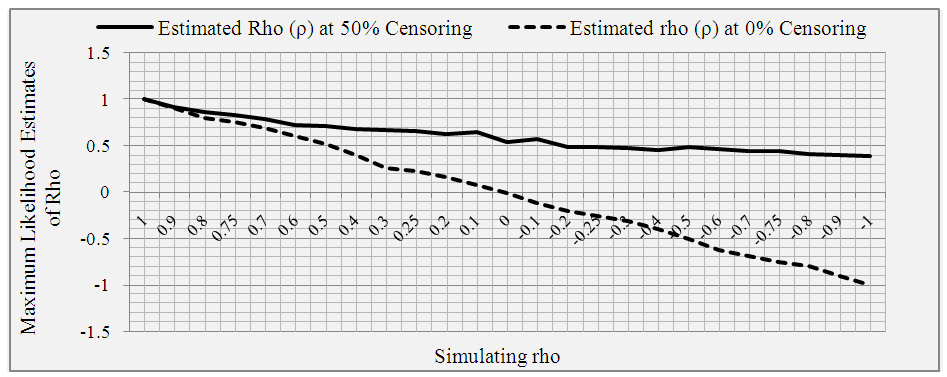 | Figure 1. The maximum likelihood estimates of the association parameters of bivariate simulated data at predetermined correlation coefficient at 0% and 50% censoring |
4. Discussion
Using simulated bivariate censored data at sets of predetermined correlation coefficients, we monitored the process and validated the model earlier developed [28]. We found that the model responded to the dictates of the inherent censoring structures and the nature of dependency between the paired set of failure times. Under 50% censoring, the maximum likelihood estimates of the association parameter tended towards zero as the predetermined correlation coefficients fell from +1.00 to -1.00 but at 0% censoring the estimates were approximate of the respective simulation correlation coefficients. In an earlier study where the model was applied, the authors found that association existed between recurrence times of infections of kidney among human subjects in North East England and the association was maximized at 0.2676 [28].In an attempt to check the procedure of the model and also to validate the model, the present study used the simulation approach to obtain standardized bivariate censored data under a set of predetermined correlation coefficients and various censoring conditions. We found an interesting trend about the estimated correlation coefficient of the simulated bivariate censored data at 50% censoring; as the predetermined correlation coefficients fell from +1.00 through 0.00 to -1.00, the maximum likelihood estimates of the association parameter of the bivariate censored data tended to zero but did not go below zero.The model produced different outcomes under the two censoring conditions. In the situation where all simulated data were presumed to be observed (0% censoring), the maximum likelihood estimates were approximate of the predetermined correlation coefficients. These finding suggested that the model worked well beside been robust. In the absence of censoring, one would expect the same (or at least an approximate) correlation coefficient between the paired data irrespective of the method used in estimating the association parameter. So, the fact that the model returned an approximate estimate as the simulation predetermined correlation coefficient indicated a good performance of the model.It was also observed during the check of the procedure that positive maximum likelihood estimates were returned even when the predetermined correlation coefficients were negative (-0.1 to -1.0) in the case of 50% censoring. One possibility for this is that each variable were subjected to 50% censoring- that is each variable were given equal chances of been censored. Although 50% censoring is a valid censoring chance, this might be different in a real life scenario. This could have been influenced by the random assignment of the censoring chances. The maximum likelihood estimates could have been negative if the proportion of the censored data were quite higher than the proportion of observed data used for the check of the model procedure.The observed positive maximum likelihood estimates at 50% censoring could also be attributed to the fact that a pair of bivariate data is mostly obtained from a single individual or related individuals, which suggest a form of dependency. For example, a study of association between the periods of time when newly born twins will live before been infected with a particular disease requires a follow-up study of twins who are naturally related. So there is high chance of dependency between the paired observation times. Furthermore, previous studies in similar settings produced similar results. In a study of characterization of the correlation between ages at entry into Breast and Pubic Hair development [24] using interval censoring approach for measuring correlations in the presence of interval censored data [23], ascertained that the likelihood was maximized at correlation (ρ) = 0.503 to 0.506.We observed that the MLE of the correlation between bivariate survival times could have been under or overestimated as the censoring proportion increased. This is quite plausible, theoretically accuracy of MLE decreases as censoring proportion gets larger [30, 31]. This may not be the case if proportion of participants censored was lower than the 50% used in this study. One way to avoid such bias is to have large sample size with a relatively long follow-up time.
5. Conclusions
The model developed previously by in Fagbamigbe et al [28] gave a satisfactory result under the two different censoring conditions. The model will work in an assessment of associations in occurrence or recurrence of diseases in both clinical and public health sciences as well as other fields of study where the occurrence of bivariate censored outcomes is imminent. The procedures of the model can also be applied to bivariate current status data. This is achievable by censoring the data, transforming the survival time and running the model using the syntax in the appendix. Using the method demonstrated in this study, research is on-going on its application to measurement of association between recurrence times of mania and depression among people undergoing psychiatric treatment of bipolar disorder. In similar vein, this method can be employed in a wide range of field including medicine, biology, epidemiology, economics and demography specifically in the study of mortality by age. For example, it can be used in studying association between times it take twins to get married or develop a particular disease or characteristics of interest.
ACKNOWLEDGEMENTS
The authors acknowledge the efforts and supports enjoyed from the Department of Epidemiology and Medical Statistics, University of Ibadan, Nigeria.
Appendix

References
| [1] | Alejandro QF: Copula Functions and Bivariate Distributions for Survival Analysis: An Application to Political Survival. 2008. |
| [2] | Diabetic Retinopathy Study Research Group: Diabetic retinopathy study. Investig Ophthalmol Vis Sci 1981, 21:149–226. |
| [3] | Duffy DL, Martin NJ, Matthews GD: Appendectomy in Australian twins. Am J Hum Genet 1995, 47:590–2. |
| [4] | Hauge M, Harvald B, Fischer M, Jensen K, Gotlieb JN, Reabild J, Shapiro R, Videbech T: The Danish twin register. Acta Genet Medicae Gemillologiae 1968, 17:315–334. |
| [5] | Le CT, Lindgren BR: Duration of ventilating tubes_ a test for comparing two clustered samples of censored data. Biometrics 1996, 52:328–334. |
| [6] | Dabrowska DM, Zhang Z, Duy DL: Graphical Comparisons of Bivariate Survival Functions With an Application to Twin Studies. Ann l’institut Henri Poincar Probab Stat 1995, 31:545–597. |
| [7] | Dabrowska DM, Doksum K, J. S: Graphical comparison of cumulative hazards for two populations. Biometrika 1989, 76:763–773. |
| [8] | Pruitt RC: On negative mass assigned by the bivariate Kaplan Meier esti-mator. Ann Stat 1991, 19:443–553. |
| [9] | Prentice RL, Cai J: Covariance and survival function estimation using censored multivariate failure time data. Biometrika 1992, 79:495–512. |
| [10] | Ghosh D: Semiparametric inferences for association with semi-competing risks data. Stat Med 2005, 24 (October 2004):1–12. |
| [11] | Hougaard P, Harvald B, Holm N V.: Assessment of Dependence in the Life Times of Twins. In Survival Analysis: State of the Art. Kluwer Academic Publisher; 1992. |
| [12] | Oakes D: A concordance test for independence in the presence of censoring. Biometrics 1982, 38:451–455. |
| [13] | Lakhal L, Rivest L, Beaudoin D: IPCW Estimator for Kendall ’ s Tau under Bivariate Censoring IPCW Estimator for Kendall ’ s Tau under Bivariate Censoring. Int J Biostat 2009, 5:1–22. |
| [14] | Kim Y: Estimation of Conditional Kendall’s Tau for Bivariate Interval Censored Data. Commun Stat Appl Methods 2015, 22:599–604. |
| [15] | Betensky RA, Finkelstein DM: A non-parametric maximum likelihood estimator for bivariate interval censored data. StatMed 1999, 18:3089–3100. |
| [16] | Li Y, Prentice RL, Lin X: Semiparametric Maximum Likelihood Estimation in Normal Transformation Models for Bivariate Survival Data. Biometrics 2008, 95:947–960. |
| [17] | Trivedi PKZ, David M: Copula modeling: An introduction for practitioners. Found Trends Econom 2005, 1:1–6. |
| [18] | Dabrowska DM: Kaplan-Meier estimate on the plane. Ann Stat 1988, 16:1475–1489. |
| [19] | Wang W, Wells M: Estimation of Kendall’s tau under censoring. Stat Sin 2000, 10:1199–1125. |
| [20] | Brown BW, Hollander M, Korwar RM: Nonparametric tests of independence for censored data, with applications to heart transplant studies. Reliab Biometry 1974, 13:33–36. |
| [21] | Weier DR, Basu AP: An investigation of Kendalls t modified for censored data with applications. J Stat Plann Inference 1980, 4:381–390. |
| [22] | Von Mises R: On the asymptotic distribution of differentiable statistical func-tions. Ann Math Stat 1947, 18:309–348. |
| [23] | Wang W, Adam Ding A: On assessing the association for bivariate current status data. Biometrika 2000, 87:879–893. |
| [24] | Christensen KY, Maisonet M, Rubin C, Flanders WD, Drews-Botsch C, Dominguez C, McGeehin M, Marcusab M: Characterization of the Correlation Between Ages at Entry Into Breast and Pubic Hair Development. Ann Epidemiol 2010, 20:405–408. |
| [25] | Groeneboom P, WellNer JA: Information Bounds and Non-Parametric Maximum Likelihood Estimation. Boston: Birkhauser; 1992. |
| [26] | Wang A: Goodness-of-Fit Tests for Archimedean Copula Models. Stat Sin 2010, 20:441–453. |
| [27] | Arkady S, Heekyung Y: Bayesian Estimation of Joint Survival Functions in Life Insurance. In ISBA 2000; 2001:1000–1004. |
| [28] | Fagbamigbe AF, Adebowale AS: A model for measuring association between bivariate censored outcomes. J Mod Math Stat 2010, 4:127 –136. |
| [29] | Bogaerts K, Lesaffre E: Estimating local and global measures of association for bivariate interval censored data with a smooth estimate of density. Stat Med 2008, 27:5941–59. |
| [30] | Kotz S: Process Capability Indices. New York: Chapman and Hall; 1993. |
| [31] | European Food Safety Authority (EFSA): Management of left-censored data in dietary exposure assessment of chemical substances. EFSA J 2010, 8:15–57. |



 under censoring have been proposed [12, 13, 20, 21], but none of the estimators is consistent when the true value of τ is not equal to zero, that is, when the marginal(s) are dependent [14]. The bias of these estimators increases as the degree of dependence increases. They had expressed τ as an integral of the bivariate survival function. Adopting the ideas presented in an early study, [22], a natural way to estimate
under censoring have been proposed [12, 13, 20, 21], but none of the estimators is consistent when the true value of τ is not equal to zero, that is, when the marginal(s) are dependent [14]. The bias of these estimators increases as the degree of dependence increases. They had expressed τ as an integral of the bivariate survival function. Adopting the ideas presented in an early study, [22], a natural way to estimate 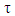 is to plug a suitable bivariate survival estimator into the integral form that defines
is to plug a suitable bivariate survival estimator into the integral form that defines  [19].Interval censoring was used in a previous study that assessed the association between bivariate current status data [23] rather than right censoring used in our study. Wang and colleague proposed a method for measuring correlations in the presence of interval censored data. The Wang et al approach was adopted in the study of characterization of the correlation between ages at entry into Breast and Pubic Hair development among teenagers [24]. Interval censoring occurs in a survival data situation when its univariate setting is considered and one is interested in a fatigue time variable T which is never observed, but can only be determined to lie below or above a random monitoring or censoring time C; where C and T are assumed to be independent [25]. The use of conditional Kendall’s τ for estimating association among bivariate interval censored data has been proposed in a recent study [14]. Similarly, Lakhal et al developed an IPCW estimator for Kendall’s
[19].Interval censoring was used in a previous study that assessed the association between bivariate current status data [23] rather than right censoring used in our study. Wang and colleague proposed a method for measuring correlations in the presence of interval censored data. The Wang et al approach was adopted in the study of characterization of the correlation between ages at entry into Breast and Pubic Hair development among teenagers [24]. Interval censoring occurs in a survival data situation when its univariate setting is considered and one is interested in a fatigue time variable T which is never observed, but can only be determined to lie below or above a random monitoring or censoring time C; where C and T are assumed to be independent [25]. The use of conditional Kendall’s τ for estimating association among bivariate interval censored data has been proposed in a recent study [14]. Similarly, Lakhal et al developed an IPCW estimator for Kendall’s 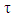 under bivariate censoring [13]. Until now, copula models are main methods used in estimating association between bivariate censored data [26] but there has been criticism against the method. Arkady et al observed that the approach is elegant and may be effective, but added that the methods sometimes prove to be insufficient depending on the type of association between the paired observations [27]. The source of this insufficiency, apparently, is the problem of dimensionality, where a two-variate survival function
under bivariate censoring [13]. Until now, copula models are main methods used in estimating association between bivariate censored data [26] but there has been criticism against the method. Arkady et al observed that the approach is elegant and may be effective, but added that the methods sometimes prove to be insufficient depending on the type of association between the paired observations [27]. The source of this insufficiency, apparently, is the problem of dimensionality, where a two-variate survival function 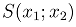 was used in order to model the behavior of three-variate joint first-life and last-survivor functions. The over reliance of copula models on Bayesian techniques by using prior distributions at the second stage in copula models makes the method difficult to use. Hence, the development of the parametric modelling of association between bivariate censored outcomes by Fagbamigbe et al [28]. The parametric model was a simpler model than the copula models and it relied less on Bayesian techniques. The study developed an alternative model for determining existence and measuring association between bivariate censored outcomes. The study illustrated the application of the model using censored outcomes of recurrences of kidney infections among people with kidney failure in North England. The authors of the study found that positive and significant associations existed between recurrence times in kidney infection and was optimized at +0.2868 [28].The present study is primarily aimed at monitoring the procedures of the model
was used in order to model the behavior of three-variate joint first-life and last-survivor functions. The over reliance of copula models on Bayesian techniques by using prior distributions at the second stage in copula models makes the method difficult to use. Hence, the development of the parametric modelling of association between bivariate censored outcomes by Fagbamigbe et al [28]. The parametric model was a simpler model than the copula models and it relied less on Bayesian techniques. The study developed an alternative model for determining existence and measuring association between bivariate censored outcomes. The study illustrated the application of the model using censored outcomes of recurrences of kidney infections among people with kidney failure in North England. The authors of the study found that positive and significant associations existed between recurrence times in kidney infection and was optimized at +0.2868 [28].The present study is primarily aimed at monitoring the procedures of the model 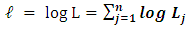 which was earlier developed to determine the possible associations between bivariate outcome using data generated via statistical simulations and to highlight dimensions that were not addressed in our previous study. Unlike the previous study that applied a real lifetime data to the method the current study used simulated that under certain conditions. Our major focus was validation of the procedures of the model using a set of predetermined correlation coefficients at 0% censoring (when all events are presumed to be observed) and 50% censoring (when all events have equal chances of being served or not).
which was earlier developed to determine the possible associations between bivariate outcome using data generated via statistical simulations and to highlight dimensions that were not addressed in our previous study. Unlike the previous study that applied a real lifetime data to the method the current study used simulated that under certain conditions. Our major focus was validation of the procedures of the model using a set of predetermined correlation coefficients at 0% censoring (when all events are presumed to be observed) and 50% censoring (when all events have equal chances of being served or not). 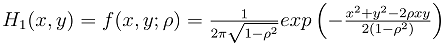
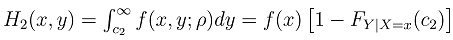
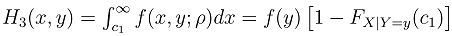
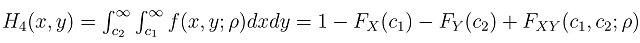
 . The corresponding cumulative distribution function of the paired variables,
. The corresponding cumulative distribution function of the paired variables, 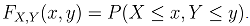 If X and Y follow a bivariate normal distribution,
If X and Y follow a bivariate normal distribution, 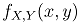 takes the form in equation 5.
takes the form in equation 5.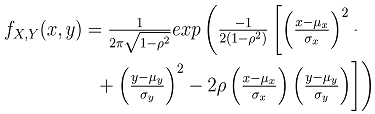
 could be expressed as
could be expressed as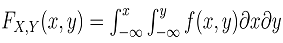
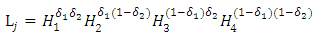
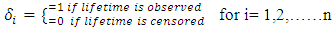
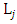 gives
gives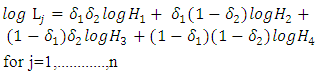
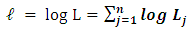
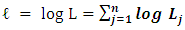 in equations 10 to obtain the Maximum Likelihood Estimation (MLE) of association parameter for each of the simulated bivariate data under the two conditions been considered. To ensure the reliability and validity of the simulated failure time data, we computed its theoretical correlation coefficient using Pearson’s product moment correlation methods. Hessian matrix was used in computing the standard error of the maximum likelihood estimations. The idea of simulation is very intuitive and has been used in literature and also in a recent study to estimate conditional Kendall’s tau for bivariate interval censored data. The study considered two different censoring levels: high right and moderate right censoring rates and set τ = 0.0; 0.3; 0.5; 0.7 where, τ = 0 implies the pairs of events are not dependent [14].
in equations 10 to obtain the Maximum Likelihood Estimation (MLE) of association parameter for each of the simulated bivariate data under the two conditions been considered. To ensure the reliability and validity of the simulated failure time data, we computed its theoretical correlation coefficient using Pearson’s product moment correlation methods. Hessian matrix was used in computing the standard error of the maximum likelihood estimations. The idea of simulation is very intuitive and has been used in literature and also in a recent study to estimate conditional Kendall’s tau for bivariate interval censored data. The study considered two different censoring levels: high right and moderate right censoring rates and set τ = 0.0; 0.3; 0.5; 0.7 where, τ = 0 implies the pairs of events are not dependent [14]. 

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
