Ohochuku N. Stephen
Department of Chemistry, Faculty of Natural and Applied Sciences, Ignatius Ajuru University of Education, Port Harcourt, Nigeria
Correspondence to: Ohochuku N. Stephen, Department of Chemistry, Faculty of Natural and Applied Sciences, Ignatius Ajuru University of Education, Port Harcourt, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The introduction of regular polygons and their constructions have always involved the regular hexagons and regular octagons. The introductory constructions of regular hexagons are by the use of circles partitioned into six equal sectors using the radius of the circle while the case of octagons use the sectoring of circles into eight equal sectors. After this the constructions of the various classes of regular polygons are delved into using either the base angle or external angle or other intricate method peculiar to the particular polygon family. This paper introduces new methods of constructing each family of regular polygon from 3-gon to 9-gon (three sided to nine sided polygons), that are suitable for introductory classes. The methods listed for each family of regular polygon are so simple as to arouse interest in polygon constructions by other methods. The methods presented here for use in introductory lessons though simple also pass as standard methods for the construction of the particular family of regular polygon.
Keywords:
Polygon Introductory construction methods
Cite this paper: Ohochuku N. Stephen, Methods of Constructing Regular Polygons Suitable for Introductory Lessons, American Journal of Mathematics and Statistics, Vol. 6 No. 6, 2016, pp. 242-250. doi: 10.5923/j.ajms.20160606.04.
Article Outline
- 1. Introduction
- 2. Methodology
- 2.2. Construction of a Regular “Triagon” (Equilateral Triangle) of Side AB
- 2.2.1. Construction of a Regular “Triagon” (Equilateral Triangle) of Side AB by Direct Method, Figure 2
- 2.2.2. Construction of a Regular Triagon (Equilateral Triangle) the Circle Sector Method, Figure 3
- 2.2.3. Construction of a Regular Triagon (Equilateral Triangle) the Intersecting Circle Method, Figure 4
- 2.3. Construction of a regular Tetragon (Square)
- 2.3.1. Construction of a Regular Tetragon (Square) of Side AB by the Intersecting Circle Method, Figure 5a
- 2.3.2. Construction of a Square via Quadrant Method, Figure 6
- 2.3.3. Tetragon via a Given Isosceles Right Angled Triangle ABC, Figure 7
- 2.4. Construction of a Regular Pentagon
- 2.4.1. From an Equilateral Triangle of Same Side. The Triagon/Circle Method, Figure 8
- 2.4.2. Regular Pentagon from Intersecting Three Collinear Circles, Figure 8a
- 2.5. Construction of Regular Hexagon of Known Side AB
- 2.5.1. Hexagon from Any Equilateral Triangle through Perpendicular Side or Angle Bisectors, Figure 9
- 2.5.2. Hexagon from an Equilateral Triangle of Same Side AB by Enlargement Procedure, Figure 10
- 2.5.3. Developing a Hexagon from Intersecting Circles with Centres at the Apexes of an Equilateral Triangle, Figure 11
- 2.6. Regular Heptagon
- 2.6.1. Development from a Triagon by the Multi Circle Procedure, Figure 12
- 2.6.2. Regular Heptagon from a Triagon by the multi Circle Procedure, Alternative Procedure, Figure 13
- 2.7. Octagon. Development of a Regular Octagon from a Square of Same Side AB
- 2.7.1. Developing a Regular Octagon from a Square of same Side via Produced Sides, Figure 14
- 2.7.2. Developing a Regular Octagon from a Square of same Side via Produced Bisectors of Sides and Internal Angles, Figure 15
- 2.7.3. Regular Octagon from regular Triagon, Figure 16
- 2.8. Regular Nonagon
- 3. Results and Discussion
- 3.1. The Triagon Constructions
- 3.2. The Tetragon Construction
- 3.3. The Pentagons
- 3.4. The Hexagons
- 3.5. The Heptagon
- 3.6. The Octagons
- 3.7. The Nonagons.
- 3.8. General Comments on the Methods
- 3.8.1. The importance of Equilateral Triangle in Polygon Construction
- 3.8.2. Additional Observations
- 3.8.3. Angle Constructions
- 4. Conclusions
1. Introduction
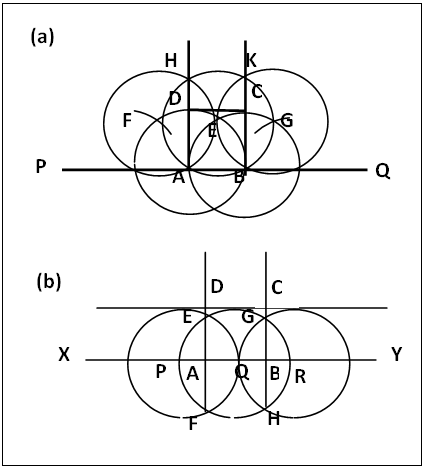
As a general definition, a polygon is defined as any geometric figure bound by three or more sides; and a regular polygon is the polygon with equal sides and equal base/external base angles [1-3]. Equilateral triangles and squares qualify as regular polygons not only by the above definition but by the fact that they also obey the rules governing the regular polygons. In some text books [1], regular polygons are presented as starting from the pentagons but in this article as in other works [2-5], regular polygons start with the equilateral triangles and the squares. These two families (the equilateral triangles and the squares) play important role in this work. From the definition, geometric plane figures bound by closed straight lines as sides are polygons; triangles and quadrilaterals form the junior families. Introductory lessons on regular polygons and their constructions are commonly demonstrated mainly with regular hexagons [2], because regular hexagons can readily be constructed by simple methods that are within the scope of elementary plane geometry, figure 1. Regular octagon is at times also used because its external base angle is readily constructed by the division of a circle into eight equal sectors as in the case of regular hexagon that is constructed by regular polygon constructions are illustrated by using their division of a circle into six equal sectors, figure 1. Other usual methods of construction that involve angle constructions and transfer of angles. Moreover many regular polygons have base/external angles difficult to construct; though there are now simple and easy methods [6] of constructing any angle. Even with these, the use of the new methods requires constructing the angles and copying it to the required place of need as a means of decongesting the work space. All these can put fear into the learner. It is needful therefore to seek for other ways of introducing the construction of the families of polygons, especially of the lower families that are always used in lessons, with simple methods which can also create interest in constructions in plane geometry.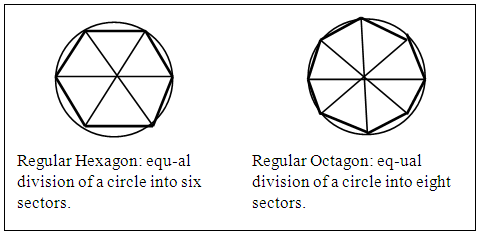 | Figure 1. Illustrations of polygon construction |
The methods so devised should also be authentic procedures for constructing the regular polygons illustrated and require only the basic knowledge in plane geometry. This is the main objective of this paper. The methods proposed here can initiate interest in the neophyte in the construction of regular polygons before the level where the use of advanced practices is needed. These simple methods devoid of special constructions and copying of angles that congest the work space with construction lines are reported hereunder.
2. Methodology
2.1. As Stated above, the Regular Polygons Start with the Equilateral Triangle through the Square, Pentagon, Hexagon, Heptagon, Octagon to Higher Members. Any method for constructing a regular polygon is acceptable but more useful is when the method constructs a regular polygon of known side length from the onset. The methods reported here under achieve the purpose. Circles play important role in the constructions that follow; therefore to simplify the naming of circles, a circle identified as circle A is the circle with centre A. From here on a named polygon or polygon means the regular type.
2.2. Construction of a Regular “Triagon” (Equilateral Triangle) of Side AB
2.2.1. Construction of a Regular “Triagon” (Equilateral Triangle) of Side AB by Direct Method, Figure 2
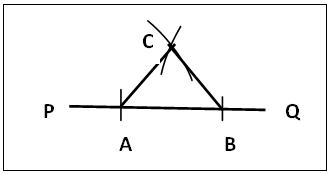 | Figure 2. Construction of a regular Triagon (Equilateral Triangle) direct method |
(a). Near the centre of a straight line PQ mark out the distance AB, figure 2.(b). A as centre and radius AB swing an arc above AB.(c). B as centre and same radius cut the arc at C. Join AC and BC. The figure ABC is the triagon (equilateral triangle).
2.2.2. Construction of a Regular Triagon (Equilateral Triangle) the Circle Sector Method, Figure 3
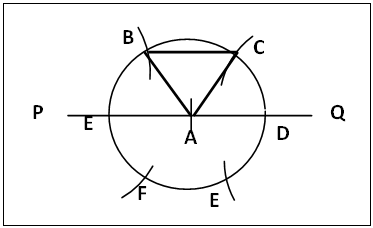 | Figure 3. Construction of a regular Triagon (Equilateral Triangle): the Circle Sector method |
(a). On a straight line PQ mark a point A. Centre A radius AB draw circle A that cuts PQ at D and E. (b). Centre E and radius AB cut circle A at B and F; centre D same radius cut circle A at C and E. Join AB, BC and AC to get the triagon ABC.
2.2.3. Construction of a Regular Triagon (Equilateral Triangle) the Intersecting Circle Method, Figure 4
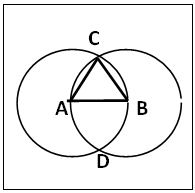 | Figure 4. Construction of a regular Triagon (Equilateral Triangle) the intersecting Circle Method |
(a). Draw the side AB of the triagon ABC, figure 4. Centre A radius AB draw circle A; centre B same radius draw circle B to intersect with circle A at C and D. Join AC and BC to get the triagon ABC.
2.3. Construction of a regular Tetragon (Square)
2.3.1. Construction of a Regular Tetragon (Square) of Side AB by the Intersecting Circle Method, Figure 5a
 | Figure 5. Construction of a Square of side AB: the intersecting Circle Method |
(a). Near the centre of PQ mark out AB. Centre A, radius AB, draw circle A; centre B, same radius draw circle B intersecting with circle A at E above AB; centre E same radius draw circle E cutting circle A at F and circle B at G.(b). Centre F same radius cut circle E at H; centre G and same radius cut circle E at K. Join AH to cut circle A at D; join BK to cut circle B at C. Join DC. ABCD is the tetragon (square). Alternatively, on a straight line XY mark PQ = QR. PQ = AB, figure 5b.(a). Centre P, radius PQ draw circle P; centre R, same radius, draw circle R; centre Q, same radius draw circle Q that cuts circle P at E and F and circle R at G and H. Join FE and HG producing each line up and each intersecting with XY at A and B respectively.(b). Centre A, same radius cut FE produced at D, centre B, same radius cut HG produced at C. Join CD. ABCD is the square.
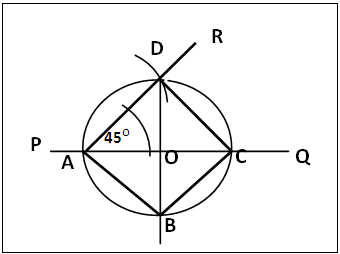
2.3.2. Construction of a Square via Quadrant Method, Figure 6
 | Figure 6. Square Construction via Quadrant Method |
(a). At point A on a straight line PQ, construct ∠RAQ = 45°, figure 6. (b). Centre A and convenient radius AB cut AR at D. Produce downwards the perpendicular from D to O on PQ.(c). Centre O and radius AO draw circle O that cuts PQ at C and DO produced at B. Join AB, BC and CD. ABCD is the tetragon.
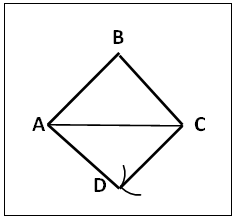
2.3.3. Tetragon via a Given Isosceles Right Angled Triangle ABC, Figure 7
 | Figure 7. Square Construction via congruent right angled Isosceles Triangles Method |
(a). Draw the isosceles right angled Triangle ACB with the base (the longer side AC) horizontal.(b). Centre A radius AB swing an arc below AC; centre C same radius cut the arc at D. Join AD and DC to get the square ABCD.
2.4. Construction of a Regular Pentagon
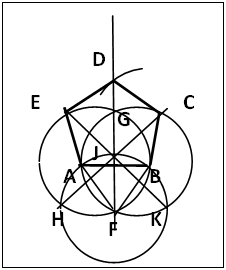
2.4.1. From an Equilateral Triangle of Same Side. The Triagon/Circle Method, Figure 8
 | Figure 8. Pentagon Construction. The Triagon/Circle Method |
(a). Draw the equilateral triangle ABF with apex F vertically below AB, figure 8. Centre A and radius AB draw circle A; centre B, same radius, draw circle B that intersects with circle A at F and G; join FG producing upwards. Centre F, same radius draw circle F that cuts circle A at H, FG at J and circle B at K.(b). Join KJ producing to cut circle A at E; join HJ producing to cut circle B at C. Join AE and BC.(c). Centre C, same radius cut FG produced at D; join CD and DE. The pentagon is ABCDE.
2.4.2. Regular Pentagon from Intersecting Three Collinear Circles, Figure 8a
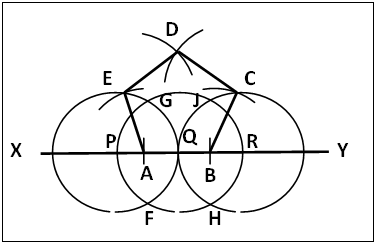 | Figure 8a. Regular Pentagon from intersecting three collinear Circles |
(a). On XY mark equal intercepts PQ = QR.(b). Centre P radius PQ draw circle P; centre R same radius draw circle R; centre Q same radius draw circle Q that cuts circle A at F and G and circle R at H and J.(c). Let the common chord FG (not drawn) of circles P and Q cut XY at A and the common chord HJ (not drawn) of circles Q and R cut XY at B; centre A same radius PQ cut circle P at E; centre B same radius cut circle R at C. Join AE and BC.(d) Centre C same radius swing arc above circle Q. Centre E same radius cut this arc above circle Q at D. Join CD and DE. ABCDE is a regular pentagon.
2.5. Construction of Regular Hexagon of Known Side AB
2.5.1. Hexagon from Any Equilateral Triangle through Perpendicular Side or Angle Bisectors, Figure 9
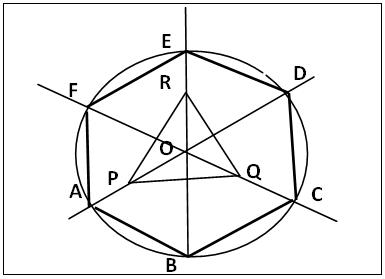 | Figure 9. Hexagon from any Triagon by Angle or Perpendicular side bisector Method |
(a). Draw any equilateral triangle PQR, figure 9; let the perpendicular (or angular) bisectors of PQ and QR (or ∠P and ∠Q) meet at O. Join RO producing all the three bisectors both ways.(b). Centre O and radius AB (side of hexagon) draw circle O that cuts the bisectors at A, (A is on OP produced), B, C, D, E and F in anticlockwise direction. Join ABCDEF as the regular hexagon.
2.5.2. Hexagon from an Equilateral Triangle of Same Side AB by Enlargement Procedure, Figure 10
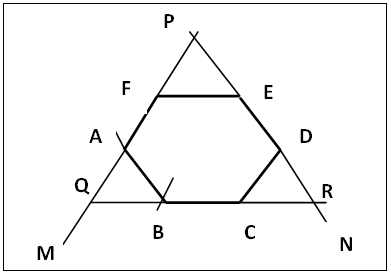 | Figure 10. Hexagon from Triagon of same side via Enlargement Procedure |
(a). Draw the given equilateral triangle PFE (ΔPFE = ΔABC given) extending PF to M and PE to N, figure 10.(b). Centre F, radius PF cut PM at A; centre A, same radius cut PM at Q; centre E, same radius cut PN at D; centre D, same radius cut PN at R. Join QR. Centre A same radius cut QR at B and centre D same radius cut RQ at C.(c). Join AB and CD. ABCDEF is the regular hexagon.
2.5.3. Developing a Hexagon from Intersecting Circles with Centres at the Apexes of an Equilateral Triangle, Figure 11
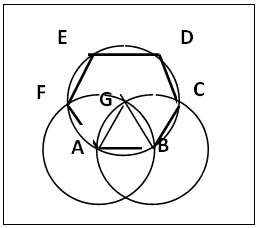 | Figure 11. Developing a Hexagon from intersecting circles with centres at the apexes of an equilateral Triangle |
(a). Draw the equilateral (triagon) ABG, figure 11. Centre A radius AB draw circle A; centre B same radius draw circle B and centre G same radius draw circle G that cuts circle A at F and circle B at C.(b). Centre F same radius cut circle G at E and centre C, same radius cut circle G at D. Join BC, CD, DE, EF and FA. ABCDEF is the hexagon.
2.6. Regular Heptagon
2.6.1. Development from a Triagon by the Multi Circle Procedure, Figure 12
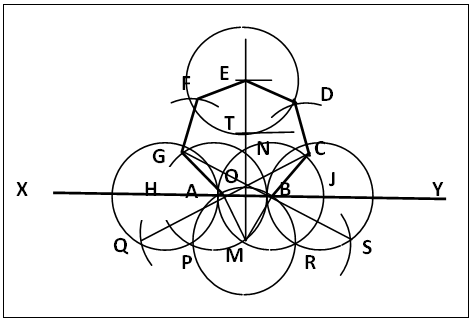 | Figure 12. Regular Heptagon via a Triagon |
(a). Near the middle of a straight line XY, draw a triagon ABM, figure 12, with vertex M vertically below AB. Centre A, radius AB draw circle A that cuts XY at H; centre B same radius draw circle B that cuts XY at J and also circle A at M and N, join MN producing upwards.(b). Centre M, same radius draw circle M that cuts circle A at P; circle B at R and MN at O. (c). Centre H same radius draw circle H; centre P same radius cut circle H at Q. (d). Centre J same radius draw circle J; centre R same radius cut circle J at S.(e). Join QO producing to cut circle B at C; join SO producing to cut circle A at G. Join BC and AG.(f). Centre O same radius cut MN produced at T, centre T and same radius cut MN produced again at E.(g). Centre E same radius draw circle E. Centre G same radius cut circle E at F, centre C and same radius cut circle E at D. Join GF, FE, ED and DC. ABCDEFG is the regular heptagon side AB, via triagon multi intersecting circles procedure, figure 11.
2.6.2. Regular Heptagon from a Triagon by the multi Circle Procedure, Alternative Procedure, Figure 13
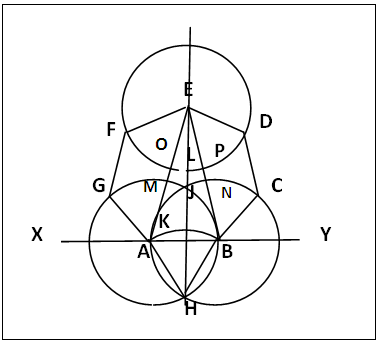 | Figure 13. Heptagon from a Triagon; Alternative Procedure |
(a). Draw the triagon ABH producing AB both ways to X and Y. Centre A, radius AB draw circle A; centre B, same radius draw circle B that cuts circle A at H and J. Join HJ producing upwards.(b). Centre H , same radius cut HJ produced at K; centre K, same radius cut equal intercepts along HJ produced at L and E. Join AE and EB that cut circle A at M and circle B at N respectively.(c). Centre E, same radius, draw circle E that cuts AE at O and BE at P respectively. Centre O, same radius cut circle A at G; centre P, same radius, cut circle B at C.(d). Centre M, same radius cut circle E at F; centre N, same radius cut circle E at D. Join BC, CD, DE, EF, FG and GA to form the regular 7-gon.
2.7. Octagon. Development of a Regular Octagon from a Square of Same Side AB
2.7.1. Developing a Regular Octagon from a Square of same Side via Produced Sides, Figure 14
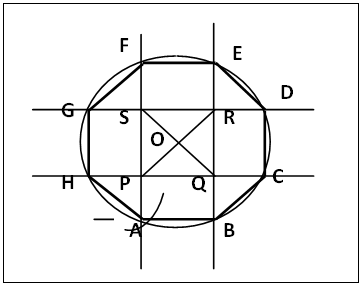 | Figure 14. Development of a regular Octagon of same Side AB as a given Square via produced Sides |
(a). Draw the square PQRS with PQ equals AB (given) producing the sides both ways, figure 14. Let O be the intersection of the diagonals.(b). Centre P radius PO cut SP produced at A. Centre O radius OA draw circle O that cuts the produced sides at points A, B, C, D, E, F, G and H (anticlockwise direction). Join adjacent points to get a regular octagon of side AB.
2.7.2. Developing a Regular Octagon from a Square of same Side via Produced Bisectors of Sides and Internal Angles, Figure 15
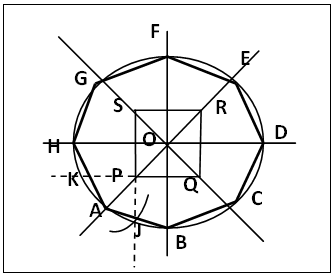 | Figure 15. Development of a regular Octagon of same Side AB as a given Square via produced bisectors of internal Angles and Sides |
(a). Draw the square PQRS with PQ equals AB (given), figure 15.Draw the perpendicular bisectors of the sides and the angular bisectors of the angles producing each bisector both ways. Let O be the intersection of these bisectors. Produce SP and QP.(b). Centre P radius PO cut SP produced at J. Centre O radius OJ draw circle O that cuts RP produced at A and the produced lines at points J, B, C, D, E, F, G, H and K (anticlockwise direction). Join adjacent points (excluding K and J) to get a regular octagon ABCDEFG of side AB.
2.7.3. Regular Octagon from regular Triagon, Figure 16
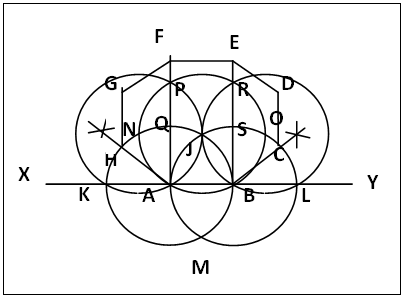 | Figure 16. Regular octagon from Triagon |
A regular octagon can be constructed from regular triagon as follows. (a). Draw the regular triagon ABJ with horizontal base AB and vertex J vertically above AB. Produce AB both ways to XY respectively. Note points A, B, and J stand for the triagon.Centre A, radius AB, draw circle A that cuts XY at K near X. Centre B, same radius draw circle B that cuts XY at L and circle A at M and J.Centre J, same radius, draw circle J that cuts circle A at N and circle B at O.Centre N, same radius, draw circle N that cuts circle J at P. Join AP that cuts circle A at Q; produce AP upwards.Centre O, same radius, draw circle O that cuts circle J at R. Join BR that cuts circle B at S; produce BR upwards.(b). With points K and P as centres and same radius bisect ∠PAK and let the bisector cut circle A at H. Join AH.With points S and L as centres and same radius bisect ∠SBL and let the bisector cut circle B at C. Join BC.(c). Centre H, same radius, swing an arc above H; centre Q, same radius, cut arc at G. Join HG.Centre C, same radius, swing an arc above C; centre S, same radius, cut arc at D. Join CD.Centre G, same radius, cut AP produced at F; join FG.Centre D, same radius, cut BR produced at E; join DE. ABCDEFGH is a regular octagon.
2.8. Regular Nonagon
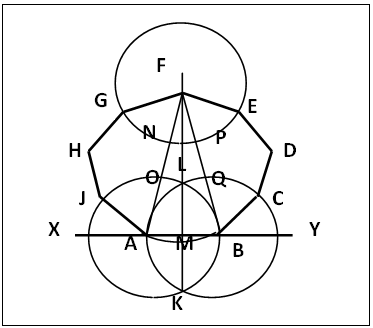 | Figure 17. Regular Nonagon |
(a) Draw a straight line XY and mark AB given, figure 17.(b). Centre A and radius AB draw circle A; Centre B, same radius, draw circle B that cuts circle A at K and L. Join KL producing upwards. Centre L, same radius cut LK at M.(c). Centre M, radius 3AB cut KL produced at F. Centre F, radius AB, draw circle F. Join FA that cuts circle F at N and circle A at O. Join FB that cuts circle F at P and circle B at Q.(d). Centre N, radius AB cut circle F at G, join FG; centre O, same radius cut circle A at J. Join AJ.Centre P, same radius AB, cut circle F at E, join EF; centre Q, same adius cut circle B at C, join BC. (e). Centre G, same radius AB swing an arc below G, centre J, same radius cut the arc at H. Join GH and HJ. Centre E same radius swing an arc below E, centre C, same radius cut this arc at D. Join DC and DE. ABCDEFGHJ is the regular nonagon.
3. Results and Discussion
3.1. The Triagon Constructions
The triagon construction in section 2.2.1 figure 2 is the normal method in vogue. The sides are equal because they are constructed with equal radius and the internal angles are equal each being 60°. Note: any adjacent points on the circumference can be joined and also to the circle’s centre to get the triagon.The circle sector method (section 2.2.2 figure 3) relies on the fact that the radius of a circle divides the circle into six equal sectors. Each sector has its straight sides equal to the radius of the circle. The chord of the sector is equal to the radius of the circle.In the intersecting circle method, section 2.2.3 figure 4, which is used as introductory construction of a regular triagon [5]. the two circles have and share common radii. The other sides are the same equal radii of equal circles. So the triangle is equilateral. Note: The procedure is the same as the direct method; in the direct method only the relevant arcs of the circles of this section 2.2.3 are shown.
3.2. The Tetragon Construction
In section, 2.3.1, tetragon construction by intersecting circles, figure 5a, circles F, E and G are of equal radius and collinear and circle E intersects with circles F and G at H and K respectively and they are a radius apart, HA is parallel to KB, both being perpendicular to AB and a radius apart (since AB is a common radius to all the circles). AD is equal and parallel to BC, so DC is tangential to circles A and B ands also equal and parallel to AB. Thus AB = BC = AD = DC and internal angles equals 90° each, hence ABCD is a square. In figure 5b, A and B are midpoints of PQ and QR, so AB = PQ. AD ǁ BC both are perpendicular to XY and AD = DC (same radius). So ABCD is a square. The above method, especially figure 5b is a fast and convenient way to construct a square without errors.In section 2.3.2 figure 6, each quadrant has a quadrant right angle isosceles triangle e.g. ΔAOD and any two neighbouring quadrants forming a semicircle house a right angled isosceles triangle e.g. Δ ACD right angled at D, with AC ( diameter) as the longer side and with equal chords as the other two sides. Combination of ΔADC with its congruent triangle ΔABC (in the other semicircle) sharing common base AC by the process described in section 2.3.2 gives a square ABCD. The construction of square ABCD could have been shortened after step (a) by using centre A with radius AD to swing arc that cuts AR at D and extended below PQ; centre D with same radius cut PQ at C; centre C, same radius cut the arc below PQ at B. Joining AB, BC and CD will give the required square. The former procedure is adopted for clarity in a lesson in the use of quadrant for square construction and also to eliminate any confusion with the procedure in section 2.3.3 that is similar.In section 2.3.3, figure 7, isosceles right angle triangle has two equal sides with included right angle. Two such congruent triangles sharing the common longer base form a square.
3.3. The Pentagons
There are two methods of constructing regular pentagons: by the use of external/internal base angle or by development from a regular triagon [4], (equilateral triangle). These methods are not simple as to be used as a demonstrative method. With the introduction of section 2.4.2 the construction of regular pentagon can now be demonstrated. The construction utilizes circles of same radius to construct the regular pentagon from an equilateral triangle of same side so the sides of the pentagon constructed are equal to that of the triagon. The construction of the internal angle CBA (of a regular pentagon) using the line HJC is not an orthodox method though it gives the expected result. Figure 8a section 2.4.2 shows a new and simple pentagon construction. Points A and B are the midpoints of PQ and QR respectively, so AB is equal to the radius of any of the circles. The regular triagon-circle procedure presents an interesting practice. Worthy of mention is the construction of regular pentagon by a procedure derived by the application of advanced algebra on polygon construction [5]. The procedure though simple does not construct a regular pentagon of predetermined side length, so it is not reported or included here.
3.4. The Hexagons
The regular hexagon has many simple and convenient methods suitable for introductory lessons apart from the method of dividing the circumference of a circle by its radius (figure 1). Regular hexagons can be constructed from any of the methods utilizing the equilateral triangle as shown above in sections 2.5.1 to 2.5.3 including the sectoring of a circle into six equal parts using the circle’s radius to obtain the hexagon in figure 1.The hexagon from the angular or perpendicular side bisectors of a triagon (section 2.5.1) has same side as the sector triangle; OA = OB (radii of same circle), each angle at O is 60°, so each base angle in triangle OAB is 60°, therefore ∠ABO is equilateral with OA = OB = AB = side of sector equilateral triangle. The radius of the circle O (as is the case in the method of equal sectoring of a circle into six parts figure 1) determines the side length of the hexagon. In the enlarged equilateral triangle, section 2.5.2, each of the small triangles, PFE say, is equilateral. FE = FA by construction, so ABCDEF is a regular hexagon of given side. This method and the sectioning of a circle into six equal sectors are suitable for regular hexagons with very short sides. In section 2.5.3, the use of three circle system with the equilateral triangle is similar to the illustration shown in figure 1; the apex G of the equilateral triangle in figure 11 locates the centre of the circle in figure 1, the points of intersections A, B, C and F on circle G are the apexes of the hexagon while AB is the length of each side of the hexagon in figure 11. AB (the side of the triagon) is the radius of each of the circles in figure 11.
3.5. The Heptagon
Before now, regular heptagon is not demonstrated because of the difficulty in constructing it from its external or internal angle. The method described in section 2.6.2, figure 13, is new and can be used as a demonstrative construction. Again the construction of the external angle CBY (of a regular heptagon) using the line QOC, figure 12, is not an orthodox method though it gives the expected result. However it appears that point J (figure 8) which is the same as point O in figure 12 is a useful point in the construction of odd numbered regular polygons by the triagon-circle procedure. This point, K figure 13 in section 2.6.2, is used in the alternative procedure for heptagon construction. The regular triagon-circle procedure here presents an interesting practice as in the case of pentagon.
3.6. The Octagons
Apart from the method of sectoring the circle into eight equal parts, shown in figure 1, there are other methods that can be used to teach the construction of regular octagons. These methods involve construction of various angles which this article tries to put to the barest minimal use. On account of this, the method of the reducing a square to a regular octagon in Blakey [7], by cutting off calculated equal lengths from each apex of the square is excluded from this report just as others in the same category because the polygon side length is to be measured or calculated. The introduction of these other new methods simplifies the matter.In section 2.7.1 figure 14 (octagon from tetragon via produced sides of tetragon), OP = PA = PH by construction; AB2 = PQ2 = 2OP2 = 2PH2 = HA2. Hence AB = HA = PQ.Section 2.7.2, (figure 15), uses produced diagonals and perpendicular side bisectors to develop the regular octagon. The square is partitioned into eight equal parts (sectors) by the bisecting lines; the circle with O as centre and radius OJ is divided into eight equal sectors as in the tetragon. Circle O cuts QP produced at K, PJ = PK, sector KOJ (lines OK and OJ not shown) = sector AOB (same radii and sector angle 45°). So KJ = AB. But AB = PQ (by construction or ΔKPJ ≡ ΔPOQ SAS). Hence KJ = PQ = AB. Note: if the squares in figures 14 and 15 are the same, the octagons constructed are the same.In section 2.7.3, figure 16, the octagon is constructed a triagon with circle assisted procedure. This method has many circles and so may be confusing, but it shows that the n-gons from n = 3 to 9 which are treated here can be constructed from a regular trigon/circle assisted method.
3.7. The Nonagons.
Section 2.8, figure 17, constructs a regular 9-gon (nonagon) by the triagon/circle procedure, a method commonly used in this work. This new method of nonagon construction is included because the few illustrative examples in the construction of polygons usually stops with octagon, the last most readily constructed polygons. The procedure is straight forward and can be used.
3.8. General Comments on the Methods
The aim of this paper is to present simple methods of constructing the lower members of polygons in introductory instruction classes. Such methods should be devoid of constructions and or copying of angles which congest the work plane and should also give polygon with known side length. The methods displayed here satisfy these purposes.
3.8.1. The importance of Equilateral Triangle in Polygon Construction
Earlier in the introduction, it was stated that the equilateral triangle plays important role in polygon constructions. Going through the method presented here for each polygon family, all can be developed from regular triagons with circle assisted constructions. One obvious observation is that polygon with even number of sides, the triagon used in the triagom cum circle procedure, is the one the apex is vertically above the horizontal base while with polygons with odd number of sides the triagon used has its apex vertically below the horizontal base. There are actually two regular triagons sharing common base (the base of the polygon under construction) formed by two intersecting circles (a constant in all the constructions by this method), the vertically opposite apexes of these two triagons with common base are the point of intersections of the two circles. It then appears that the equilateral triangle is a basic element in the construction of any regular polygon, when coupled with circles of same radii. The regular tetragon (square) is also an important element in the construction of regular 8-gon, sections 2.7.1 figure 14 and section 2.7.2 figure 15. A regular 6-gon can also be developed from a regular tetragon (square) of same side length. A square is drawn. The midpoint O of the diagonal as centre and the side of the square as the radius circle O is drawn. Equal sectoring of the circumference of circle O with its radius gives points along the circumference as apexes of a regular 6-gon. The method is similar to equal division of a circle into six sectors figure 1 in the introduction section with the square providing the centre and radius of the circle and hence the side of the hexagon. Another aspect of the triagon-circle procedure is the use of constant radius (the side of the triagon) all through the construction. This makes the construction easy once the required centres can be correctly identified.
3.8.2. Additional Observations
Additional observations useful to the learner includes the following: the line passing through the points of intersections of two circles is perpendicular to the line of centres; if the two circles share common radius the line through the intersecting points is the perpendicular bisector of the line of centres e.g. line GF in section 2.4.1 figure 8 and can be used in section 2.5.1, figure 9 to get the angle or side bisectors of the triagon; but for the congestion of the work space, only relevant arcs are shown. In general, any arc drawn in a construction is part of a circle (the general work horse/facilitator in plane geometric constructions) with known centre.
3.8.3. Angle Constructions
One main difficulty in regular polygon construction is the inability to construct most of the base or external base angle. Hitherto such angles are copied from the protractor until the emergence of methods for the equipartition of angles into any number of parts [6]. Sections 2.4.1 and 2.4.2 introduce two respective methods of constructing ∠72 (external angle of a regular pentagon) and section 2.5.3 figure 12 shows a modification of section 2.4.1 for the construction of 513/7o (the external angle of a regular heptagon). These methods suggest the existence of other methods of constructing the angles of some of these polygons and which have not been investigated.
4. Conclusions
For introductory teaching on regular polygons there are enough simple constructions. These new methods as detailed in sections 2.2.2, 2.3.1, 2.3.2, 2.3.3, 2.4.2, 2.5.1, 2.5.2, 2.5.3, 2.6.1, 2.6.2, 2.7.1, 2.7.2, 2.7.3 and 2.8 are new methods that can be added to any existing procedures used for illustrative constructions. An instructor can choose from the lot of methods listed. These methods though simple they are equally standard procedures applicable to each polygon class. For beginners with preliminary skill in geometric constructions, these constructions will not only be readily assimilated but will also arouse more interest to spur them to higher methods of constructions in this field.
References
| [1] | Bamiro O A, Elekwa I, Okolie Onyedinma A C B, Okorie O O, and Anyabolu I C. 1985. Introductory Technology for Schools and Colleges. Evans Brothers (Nigeria Publishers) Ltd, Jericho Road, Ibadan, Nigeria, p14. |
| [2] | Macrea M F, Kalejaiye A O, Chima Z I, Garba G U, Channon J B, MacLeish Smith A, and Head H C. 2008. New General Mathematics for senior Secondary Schools UBE Edition. Pearson Educational Ltd, Edinburh Gate, Harlow, Essex CM 20 2EJ, England, p9. |
| [3] | Bailey, Day, FREY, Howard, Hutchens, Mclain, Moore-Harris, Olt, Pelfrey, Prie, Vielhaber, and Willard. Mathematics: Applications and Concepts Course 2. Florida Edition, fl.msmaths.net McGraw Hill Glencoe. New York. Chapter 10-7 pp446-447. |
| [4] | Comparative Education Study and Adaptation Centre, CESAC. 1986. Introductory Technology for Junior Secondary Schools Text book 2, p16. |
| [5] | Dynamics of Polygons.org Construction of Regular Polygons. |
| [6] | Ohochuku, N. S. 2015. Equipartition of Plane Geometric Angles into any Number of Parts. Journal of Applied Mathematics, 5(4). Pp84 – 87. http://journal.sapub.org/am. |
| [7] | Blakey, J. Intermediate Mathematics. Cleaver-Hume Press Ltd. Kesington London. 1960, 2nd edition, p186. |





















 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML