-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2016; 6(6): 238-241
doi:10.5923/j.ajms.20160606.03

Elementary Proofs of the Jordan Decomposition Theorem for Niloptent Matrices
Mohamed Kobeissi, Bilal Chebaro
Larifa Laboratory, Faculty of Sciences, Lebanese University of Beirut, Lebanon
Correspondence to: Mohamed Kobeissi, Larifa Laboratory, Faculty of Sciences, Lebanese University of Beirut, Lebanon.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper we use elementary concepts of linear algebra to show that a nilpotent matrix is similar to a Jordan matrix.
Keywords: Jordan decomposition, Nilpotent matrices
Cite this paper: Mohamed Kobeissi, Bilal Chebaro, Elementary Proofs of the Jordan Decomposition Theorem for Niloptent Matrices, American Journal of Mathematics and Statistics, Vol. 6 No. 6, 2016, pp. 238-241. doi: 10.5923/j.ajms.20160606.03.
Article Outline
1. Introduction
- The Jordan decomposition theorem for nilpotent matrices is treated in simple way. While the result is known, the interest of our proofs lies in their simplicity. Note that the usual proofs are mostly based on module theory and/or quotient spaces. Definition 1 A nilpotent Jordan block of size n, denoted
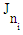 , is a square matrix of the form:
, is a square matrix of the form:  Definition 2 A nilpotent Jordan matrix is a block diagonal matrix of the form:
Definition 2 A nilpotent Jordan matrix is a block diagonal matrix of the form: 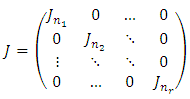 where each
where each 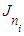 is a nilpotent Jordan block.Theorem 1 Let E be a vector space over a field K, of finite dimension n, and f a linear operator on E, nilpotent of index p. There exists some basis B, in which the matrix representing f in B is a Jordan matrix. Theorem 1 can be expressed in matrix form as follows: Theorem 2 Every nilpotent
is a nilpotent Jordan block.Theorem 1 Let E be a vector space over a field K, of finite dimension n, and f a linear operator on E, nilpotent of index p. There exists some basis B, in which the matrix representing f in B is a Jordan matrix. Theorem 1 can be expressed in matrix form as follows: Theorem 2 Every nilpotent 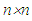 matrix N of index p is similar to an
matrix N of index p is similar to an 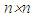 Jordan matrix J in which the size of the largest Jordan block is
Jordan matrix J in which the size of the largest Jordan block is 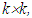 where k is the rank of N. A. Galperin and Z. Waksman [1] used elementary concepts to show that
where k is the rank of N. A. Galperin and Z. Waksman [1] used elementary concepts to show that 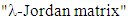 is similar to Jordan matrix. Gohberg and Goldberg [2] gave an algorithm that builds Jordan form of an operator A on an n-dimensional space if the Jordan form restricted to an n1 dimensional invariant subspace is known. In what follows, we give two proofs of theorem 2. The first by using elementary operations on matrices, and the second by using a decomposition of E into direct sums of subspaces.
is similar to Jordan matrix. Gohberg and Goldberg [2] gave an algorithm that builds Jordan form of an operator A on an n-dimensional space if the Jordan form restricted to an n1 dimensional invariant subspace is known. In what follows, we give two proofs of theorem 2. The first by using elementary operations on matrices, and the second by using a decomposition of E into direct sums of subspaces.2. Method 1 - Elementary Operations
- We shall prove theorem 2 by induction. The following two lemmas are first proved: Lemma 1 There exists a matrix A representing f having the following form:
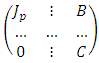 Proof 1 As f is nilpotent of index p, there exists
Proof 1 As f is nilpotent of index p, there exists 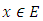 such that
such that 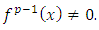 The family
The family 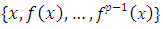 is then linearly independent
is then linearly independent 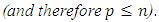 Suppose the contrary, then there exist constants
Suppose the contrary, then there exist constants 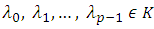 not all zero such that
not all zero such that 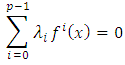 Now let
Now let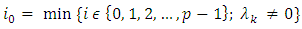 therefore
therefore 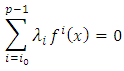 and
and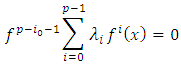 i.e.
i.e. 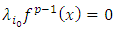 and
and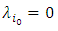 , which is a contradiction By the incomplete basis theorem, there exist vectors
, which is a contradiction By the incomplete basis theorem, there exist vectors 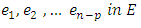 such that the family
such that the family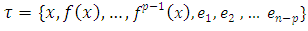 spans E. The matrix
spans E. The matrix 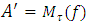 representing f in that basis has the needed property.The lemma 2 below is the key to prove our theorem. We shall prove (again in two ways!) that the bloc matrix B found in lemma 1 is in fact the zero matrix. Lemma 2 There exists a matrix representing f having the form:
representing f in that basis has the needed property.The lemma 2 below is the key to prove our theorem. We shall prove (again in two ways!) that the bloc matrix B found in lemma 1 is in fact the zero matrix. Lemma 2 There exists a matrix representing f having the form:  Proof 2 method 1: The first proof is based on elementary matrix calculations. For this let the triangular matrix
Proof 2 method 1: The first proof is based on elementary matrix calculations. For this let the triangular matrix 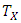 defined as follows:
defined as follows: 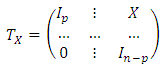 We can easily check that
We can easily check that 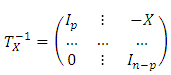 Define the matrix A' by
Define the matrix A' by 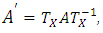 clearly:
clearly: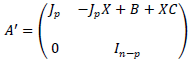 Let
Let 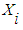 and
and 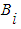 be the i-th rows of X and B respectively, then
be the i-th rows of X and B respectively, then 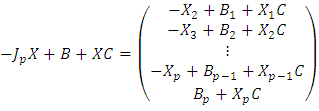 Now choose
Now choose 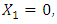 and for
and for 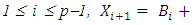
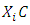 , we obtain a matrix A' , similar to A , of the form
, we obtain a matrix A' , similar to A , of the form 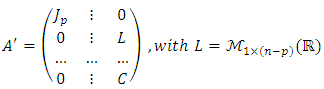 A simple calculation yields:
A simple calculation yields: 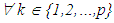
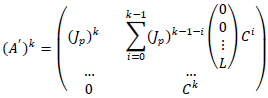 As
As 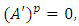 then
then 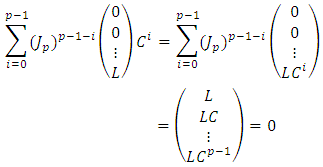 Therefore L=0, and hence
Therefore L=0, and hence 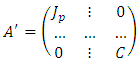 method 2: Let
method 2: Let 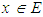 such that the family
such that the family 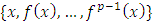 is linearly independent. Complete the basis of E by vectors
is linearly independent. Complete the basis of E by vectors 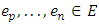 i.e. the family
i.e. the family 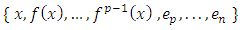 is basis of E. Let x be in E, then
is basis of E. Let x be in E, then 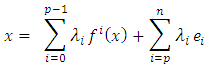 And define the linear operator:
And define the linear operator: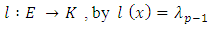 We now state and prove the following three properties about the linear form l: • property 1: The family
We now state and prove the following three properties about the linear form l: • property 1: The family 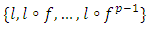 is linearly independent in
is linearly independent in 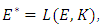 the dual of ESuppose the contrary, then there exist scalars
the dual of ESuppose the contrary, then there exist scalars 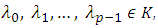 not all zeros, with
not all zeros, with 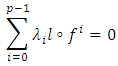 Denote
Denote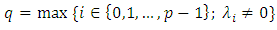 then
then 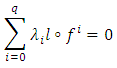 and
and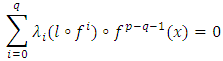 implies that
implies that 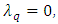 which contradicts our hypothesisDenote now
which contradicts our hypothesisDenote now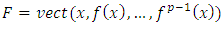
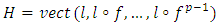 and let G be the set of all
and let G be the set of all 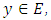 such that
such that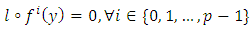 • property 2: The subspace G of E is stable by f- for all
• property 2: The subspace G of E is stable by f- for all 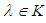 and all
and all 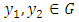 , and
, and 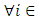
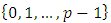 ; we have
; we have 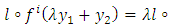
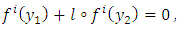 then
then 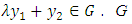 is therefore a subspace of E- If
is therefore a subspace of E- If 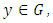 then
then 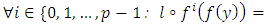
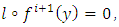 and
and 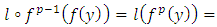
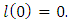 Therefore,
Therefore, 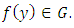 And finally, • property 3:
And finally, • property 3: 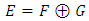 - If
- If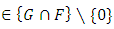 , then there exist
, then there exist 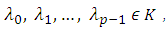 not all zeros, such that
not all zeros, such that 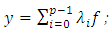 by letting
by letting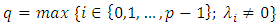 then
then 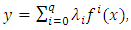 and
and 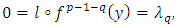 which contradicts the hypothesis- Let
which contradicts the hypothesis- Let 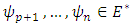 such that
such that 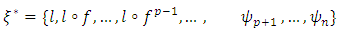 is a basis of
is a basis of 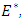 and let
and let 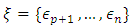 be a basis of E whose dual basis is
be a basis of E whose dual basis is 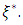
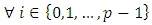 , and
, and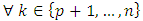 ;
; 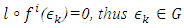 - If
- If 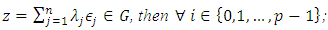
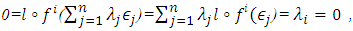 hence
hence 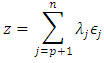 Thus
Thus 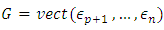 hence
hence 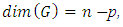 and Consequently
and Consequently 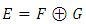 Is it now simple to see that the matrix representing f in the basis
Is it now simple to see that the matrix representing f in the basis 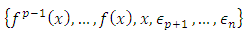 of
of 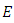 is of the form:
is of the form:  The first proof of our theorem can now be completed. For
The first proof of our theorem can now be completed. For 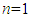 and
and 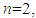 the result is obvious; Assume the result holds up to
the result is obvious; Assume the result holds up to 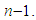 By lemma 2, there exists an invertible matrix
By lemma 2, there exists an invertible matrix 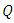 such that
such that 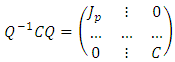 By the induction hypothesis, the exists an invertible matrix P such that
By the induction hypothesis, the exists an invertible matrix P such that 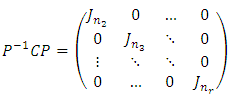 Let n1=p, and then
Let n1=p, and then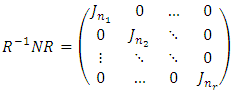 this completes the proof.
this completes the proof.3. Method 2 - Decomposition of E into Direct Sums
- The second proof was suggested by Rached Mneimné [4] during my visit to the department of Mathematics at Université Diderot in April 2015. The following theorem is on the decomposition of E into direct. Theorem 3 Let E be a vector space over a field K, of finite dimension n, and f is a linear operator on E, nilpotent of index p. There exists
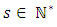 and subspaces
and subspaces 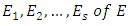 such that: a)
such that: a) 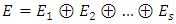 b)
b) 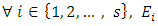 is stable by fc) the operator
is stable by fc) the operator 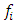 , restriction of
, restriction of 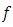 over
over 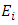 , is nilpotent of index
, is nilpotent of index 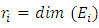 Proof 3 The proof is by induction. It is obviously true for
Proof 3 The proof is by induction. It is obviously true for 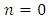 and
and 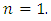 Now suppose that the result holds up to
Now suppose that the result holds up to 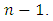 As f is nilpotent, then
As f is nilpotent, then  and then by the induction hypothesis, there exists
and then by the induction hypothesis, there exists 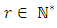 and subspaces
and subspaces 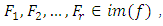 such that:a)
such that:a) 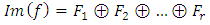 b)
b) 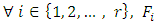 is stable by fc) the operator
is stable by fc) the operator 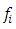 , restriction of
, restriction of 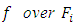 , is nilpotent of index
, is nilpotent of index 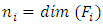 As
As 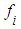 is nilpotent of order
is nilpotent of order 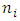 , then by lemma 1, there exists
, then by lemma 1, there exists 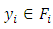 such that
such that 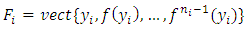 Moreover
Moreover 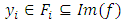 , then there exists
, then there exists 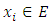 such that
such that 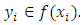 Denote
Denote 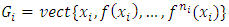 and
and 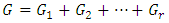 Six properties for the subspaces
Six properties for the subspaces 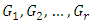 are stated and proved: 1.
are stated and proved: 1. 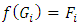 In fact, if
In fact, if 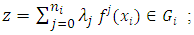 then
then 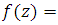
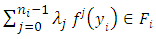 and
and 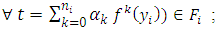
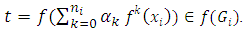 Thus
Thus 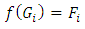 2.
2. 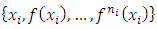 is a basis of
is a basis of 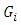 If
If 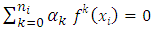 , then
, then 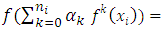
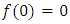 i.e.
i.e. 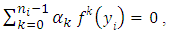 and as the family
and as the family 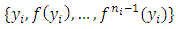 is linearly independent, then
is linearly independent, then 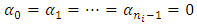 and
and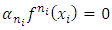 , and
, and 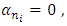 Therefore
Therefore 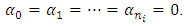 3.
3. 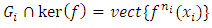
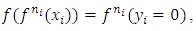 then
then 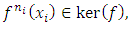 and
and 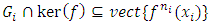 if
if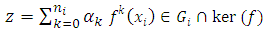 , then
, then 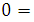
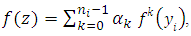 and
and 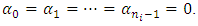 Therefore
Therefore 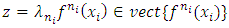 4.
4. 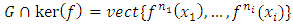 Let
Let 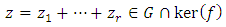 with
with 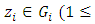
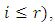 then
then 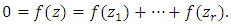 As
As 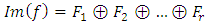 and
and 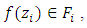 then
then 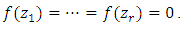 By the previous property, there exists
By the previous property, there exists 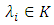 such that
such that 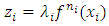 , and
, and 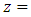
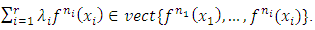 Therefore
Therefore 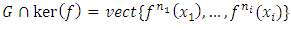 5.
5. 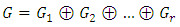 If
If 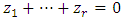 with
with 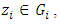 then by the previous property
then by the previous property 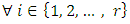 there exists
there exists 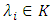 such that
such that 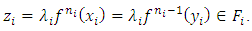 As the subspaces
As the subspaces 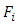 are in direct sum, then
are in direct sum, then 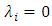 and
and 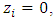 therefore
therefore 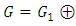
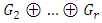 6.
6. 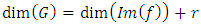
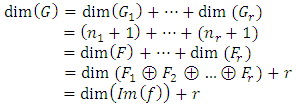 The proof of theorem 3 can now be completed as follows: Let now H be a complement of
The proof of theorem 3 can now be completed as follows: Let now H be a complement of 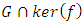 in
in 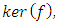 then:
then: 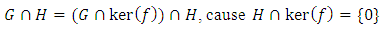 | (1) |
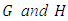 are in direct sum, and:
are in direct sum, and: 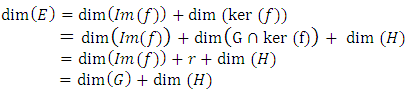 Therefore,
Therefore, 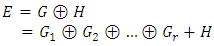 And
And 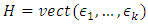 with
with  is a basis of H.The second proof of theorem can be obtained. We can now check that the matrix representing
is a basis of H.The second proof of theorem can be obtained. We can now check that the matrix representing 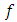 in the basis is:
in the basis is: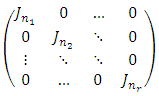
ACKNOWLEDGEMENTS
- The authors are thankful to Salim Kobeissi, Professeur aggregé at Université Pierre Mendès France, Grenoble II, and to Rached Mneimné, Associate Professor at Université Diderot, Paris 7, for their valuable comments.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML