1. Introduction

In the past it is recorded that the population of Bangladesh has had grown at an increasing rate up until 1975. Since then the Government of Bangladesh adopted various policies to control its fast growing population. Policies for example, family planning, educating people, participation of females in the payroll, and a condition on the age at first marriage (year 18 for female and 20 for mate) are in action at present. Bangladesh is a poor country it always depends on foreign aid and donation form received from donor agencies, e.g., IMF, WB, Asian Development Bank (ADB), United Nation Fund for Population Association (UNFPA) and many other smaller donors. These donor countries always put condition to increase the gross domestic product (GDP) per head keeping the inflation at a tolerable level. The government has no option other than those stated above to control its population growth at a manageable level to maintain a healthy per capita GDP. There is another alternative to increase the GDP per person by increasing the domestic product keeping the population at a low level.

Islam and Ali (2004a) reported that natural increase of population of Bangladesh is decreasing from 1974 to 1998. In Bangladesh, Islam and Ali (2004b) showed that intrinsic growth rate for female population is starting to reduce from the period 1961-1974. Islam (2012a) observed that intrinsic growth rate for male population is starting to reduce from the period of 1961-1974 up to the period of 1991-2001.

To reduce the population growth for Bangladesh a forecast model is proposed in this paper. The proposed autoregressive time trend forecast model predicts the population growth from 2004 to through 2043.

This paper is organized as follows. In section 2 data and sources of data and variables of interest are discussed. Section 3 presents the model and the methodology. Empirical results of the forecasts and the forecast model adequacy are given in section 4. Section 5 concludes the paper.

2. Data, Sources of Data and the Variable

Annual data on Bangladesh population from 1965 to 2003 has been taken from the DX-Data base available in the Computer Lab of the School of Business of James Cook University, Australia (provided by Dr. A. B. M. Rabiul Alam Beg while he was visiting the department of Statistics of Rajshahi University, Bangladesh for his sabbatical assignment). The population is measured in thousands. To find out the population growth rate this paper considers the continuously compounded rule as 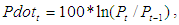where and 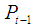are the population at time t and time t - 1 respectively.

3. The Model and the Methodology

Initially a linear time trend model 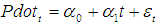for was fitted with a little success. This linear time trend model is then updated by including autoregressive terms up to lag 2. The following autoregressive time trend model for forecasting population growth is considered in this paper.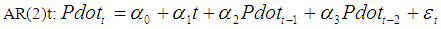

(1)

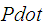Where is defined as above, 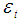is a random error term with mean zero and constant (unknown) variance. 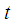is the linear time trend term, 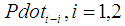are the lag dependent variables included in (1). 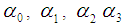, are the parameters to be estimated along with the unknown error variance.

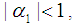
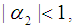
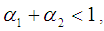
Since this is an autoregressive model we require the condition on the estimated parameters should be 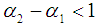for stability of the model.

For model validation, the cross validation predictive power (CVPP) denoted, 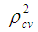is computed by

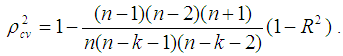Where n is the number of cases, k is the number of regressors in the model, and R² is the coefficient of determination of the model. The shrinkage of the model is equal to the absolute value of 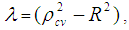(Steven, 1996). Closer the value of λ to zero, better is the prediction. It is noted that this technique was also used as model validation technique (Islam, 2005; 2007a; 2007b; 2008; 2011; 2012b; 2012c; 2013; 2014; Islam and Beg, 2009; 2010; Islam & Hossain, 2013a; 2013b; 2014a; 2014b; Hossain & Islam, 2013; Islam et al., 2013; 2014; Hossain et al., 2015; Islam & Hossain, 2015; Islam & Hoque, 2015).

Model (1) is estimated by the ordinary least squares (OLS) method using SHAZAM. The empirical results with discussion are given in section 4.

4. Empirical Results and Discussion of the Results

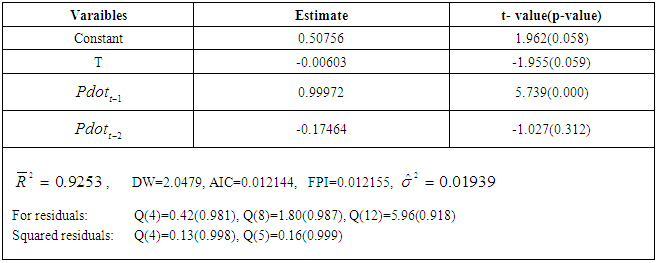
The OLS estimated parameters of the model (1) are reported in the following Table-1.

Table 1. Parameter estimates and other statistics of model (1)

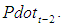The estimated coefficients of model (1) are all significant at 10% level except The 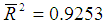indicates that approximately 93% of the total variation in is explained by the explanatory variables of the model. Akaike’s information criterion (AIC), Akaike’s final prediction error (FPE) and estimated error variance are all small. These values are useful for model’s prediction performance.

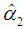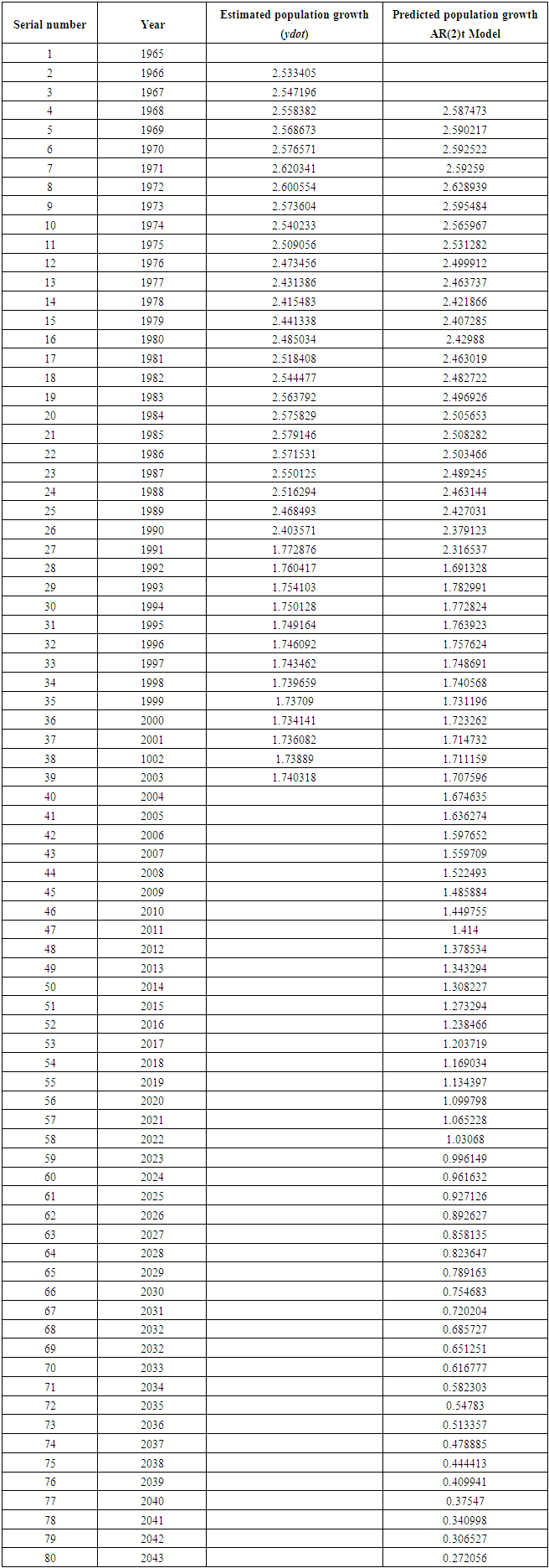
Although the estimate is statistically significant at the conventional level, its value is close to one. In that case Dickey-Fuller unit root test (Dickey & Fuller, 1978, 1981) could not distinguish between the unit root and near unit root. Eventually Dickey-Fuller test concludes that the series is nonstationary. However, the Ljung-Box (1978) Q-statistics pass the model adequacy test. Moreover, the condition of the stability of the AR(2)t process is satisfied. Furthermore, the low values of 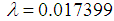indicates that the fitted model provides better predictions for the future years. Consequently, one can adopt this model for forecasting purpose. The forecasts based on the estimated model (1) and the observed population growth values are given in table 2. A graph shows the downward movement of the population growth for the years 1965 to 2043.

Table 2. The Observed and the predicted growth rate of the population of Bangladesh

In table 2 population growth for the observed data from year 1986 shows a decreasing trend in population growth within the sample. The predicted population growth by the AR(2)t model of this paper shows a decreasing trend from year 1986 to 2043 throughout. This is consistent with the observed trend in population growth from 1986 to 2003.

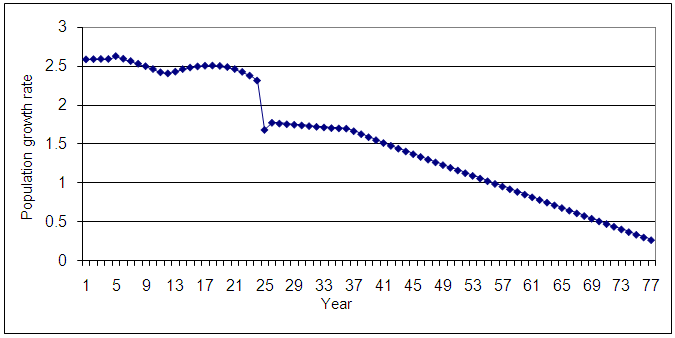Figure 1. Predicted population growth rate of Bangladesh for the years 1968-2043 indexed by 1, 2……,77

5. Conclusions

In predicting the population growth of Bangladesh for the years 1965 to 2043 we have adopted an autoregressive with time trend model for the observed growth rate. The estimated autoregressive parameters satisfy the stability conditions. Furthermore, based on the Q statistics, 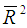and t-test values this model is found to be adequate for forecasting the population growth of Bangladesh. The shrinkage parameter λ also produces a small value indicating that the performance of the prediction model is reliable. This model can be used for various policy decisions purpose.