R. K. Ansah 1, R. K. Boadi 2, W. Obeng-Denteh 2, A. Y. Omari-Sasu 2
1Department of Mathematics and Statistics, UENR, Sunyani, Ghana
2Department of Mathematics, KNUST, Kumasi, Ghana
Correspondence to: R. K. Ansah , Department of Mathematics and Statistics, UENR, Sunyani, Ghana.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The Birch and Swinnerton-Dyer Conjecture is a well known mathematics problem in the area of Elliptic Curve. One of the crowning moments is the paper by Andrew Wiles which is difficult to understand let alone to appreciate the conjecture. This paper surveys the background of the conjecture treating the ranks of the elliptic curves over the field of rational numbers. Then we present major results like the theorems of Mordell and Mazur leading us to the current state of the conjecture.
Keywords:
Elliptic curve, Birch and Swinnerton-Dyer Conjecture, Additive abelian group, Mordell theorem
Cite this paper: R. K. Ansah , R. K. Boadi , W. Obeng-Denteh , A. Y. Omari-Sasu , Review of the Birch and Swinnerton-Dyer Conjecture, American Journal of Mathematics and Statistics, Vol. 6 No. 4, 2016, pp. 182-189. doi: 10.5923/j.ajms.20160604.07.
1. Introduction
L. J. Mordell began his famous paper with the words “Mathematicians have been familiar with very few questions for so long a period with so little accomplished in the way of general results, as that of finding the rational points on elliptic curves" [1]. Elliptic curves have a lot of applications, this because it possible to take two Points on the curve and generate a third point. In fact, we will show that by defining an addition operation and introducing an extra point called the point of infinity, the points on an elliptic curve form an additive abelian group [12]. There are still a number of significant open questions specific to the theory of elliptic curves themselves, such as the conjecture of Birch and Swinnerton-Dyer which would give a much more precise description of the beautiful arithmetic that exists for points on elliptic curves [14].
2. The Algebra and Geometry of Elliptic Curves
Elliptic curves are functions defined by equation of the form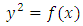 | (1) |
 has no multiple roots. The cubic equation
has no multiple roots. The cubic equation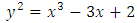 does not define an elliptic curve, because
does not define an elliptic curve, because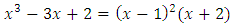 has 1 as a multiple root. Similarly
has 1 as a multiple root. Similarly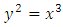 is not an elliptic curve, but
is not an elliptic curve, but is an elliptic curve.The general form of an elliptic curve is given below
is an elliptic curve.The general form of an elliptic curve is given below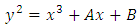 | (2) |
Where 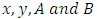 belong to a specified field such as
belong to a specified field such as 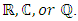 General we use
General we use 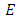 to represent an elliptic curve. If we wish to consider points in a field
to represent an elliptic curve. If we wish to consider points in a field 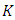 we write
we write 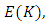 which is defined as below.
which is defined as below.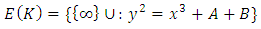 | (3) |
2.1. We can Use Geometry to Make the Points of an Elliptic Curve into a Group
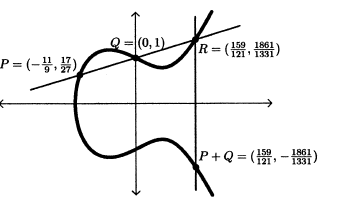
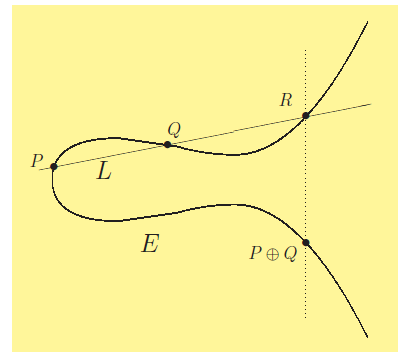 | Figure 1. P + Q |
2.2. Properties of "Addition" on Elliptic Curve
The addition law on an Elliptic curve has the following properties: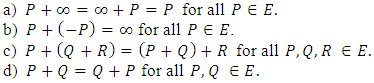 In other words, the addition law + makes the points of E into a commutative group. [11]
In other words, the addition law + makes the points of E into a commutative group. [11]
2.3. The Addition Operation is Summarized below
Let E be an elliptic curve defined by 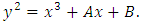 Let
Let 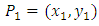 and
and  be points on
be points on 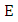 with
with 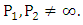 We the define
We the define 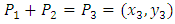 as follows 1. If
as follows 1. If 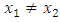 then
then 
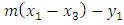 where
where 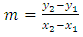 .2. If
.2. If 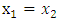 but
but  then
then 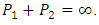 3. If
3. If 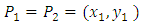 and
and 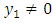 then
then 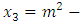
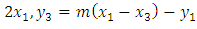 where
where 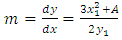 .4. If
.4. If 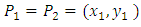 and
and 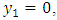 then
then 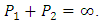 Also we define
Also we define 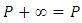 for all points
for all points 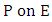 [12].
[12].
2.3.1. Example 1
Let E be the curve 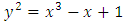 and suppose we know the point
and suppose we know the point 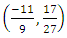 and
and 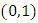 lies on the curve. To find another point on. In the notation of elliptic curve addition we have:
lies on the curve. To find another point on. In the notation of elliptic curve addition we have: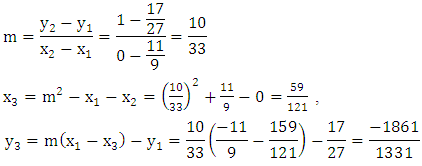
 | Figure 2. y2 - x + 1 and its addition law |
2.3.2. Example 2
The set 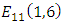 is the set of integers
is the set of integers 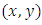 that satisfy
that satisfy 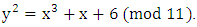 We can see that
We can see that 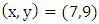 is the set as
is the set as 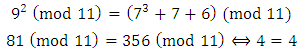 To find all the points in
To find all the points in 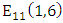 we find all the possible values
we find all the possible values 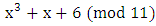 and then see what values of
and then see what values of 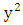 will match. There are 11 choices of
will match. There are 11 choices of  the integers
the integers  Subbing these values in turn into the cubic and reducing modulo 11 will give us the possible values of
Subbing these values in turn into the cubic and reducing modulo 11 will give us the possible values of 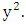
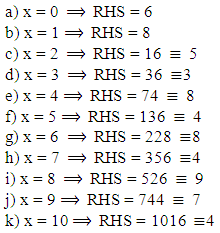 So we can see that the possible values of
So we can see that the possible values of  cannot be 0, 1, 2 or 10.Next examine the 10 possible values of
cannot be 0, 1, 2 or 10.Next examine the 10 possible values of 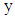 and identify which values of
and identify which values of  they could be paired with to give a point on the curve.
they could be paired with to give a point on the curve.
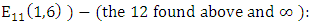
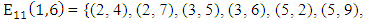
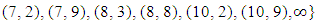
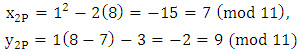 So in
So in 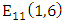 we find
we find 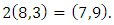
3. Elliptic Curves over Finite Fields
Let 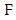 be a finite field and
be a finite field and  an elliptic curve defined over
an elliptic curve defined over  Since there are only a finite number of pairs
Since there are only a finite number of pairs 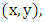 with
with 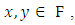 the group
the group 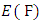 must itself be finite. In this section. We discuss the basic theory of elliptic curves over finite fields and also we will state Hasse’s theorem which gives a bound of the size of the group defined by
must itself be finite. In this section. We discuss the basic theory of elliptic curves over finite fields and also we will state Hasse’s theorem which gives a bound of the size of the group defined by 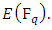 We also look at methods to find the order of a point in
We also look at methods to find the order of a point in  [12].
[12].
3.1. Example 4
Let 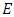 be thr curve
be thr curve 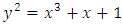 over
over 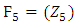
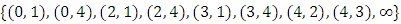
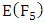 has order 9.
has order 9. 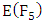 is cyclic and generated by (0,1).
is cyclic and generated by (0,1).
3.2. Methods to determine the order of 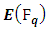
Hasse’s theorem gave bounds for the group of points on an elliptic curve over a finite field. In this section we discuss methods for determining the group order exactly. Suppose we have an elliptic curve defined over a finite field 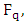 we can determine the order of
we can determine the order of 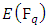 by listing the points. We can then determine the order of
by listing the points. We can then determine the order of 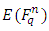 for all
for all 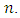 [12]
[12]
3.2.1. Theorem 1
Let 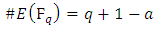 write
write 
 then for all
then for all 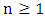
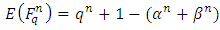 | (4) |
3.3. Example 3
Let 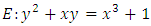 be an elliptic curve
be an elliptic curve 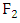 satisfies
satisfies 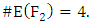 Therefore
Therefore 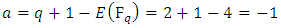 and we obtain the polynomial
and we obtain the polynomial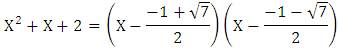
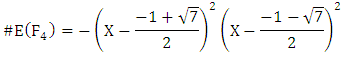 We could compute the last expression directly, but better use the recurrence relation
We could compute the last expression directly, but better use the recurrence relation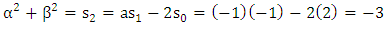 So,
So, 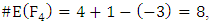 (as we calculated when listing points).
(as we calculated when listing points).
3.4. Legendre Symbol
To make a list of all the points on 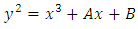 over a finite field, we listed every possible value of
over a finite field, we listed every possible value of 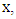 and then found the square roots,
and then found the square roots,  of
of 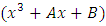 if they existed. This procedure will be the basis for a simple point counting algorithm.The Legendre symbol we can generalize this to a finite field
if they existed. This procedure will be the basis for a simple point counting algorithm.The Legendre symbol we can generalize this to a finite field 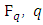 odd, by defining for
odd, by defining for 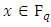
 We can now give a more accurate solution to the number of points on
We can now give a more accurate solution to the number of points on 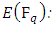
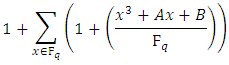
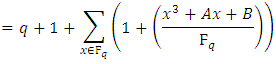
3.4.1. Theorem 2
Let E be an elliptic curve 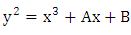 over
over 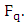 Then
Then 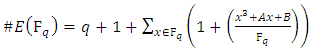 | (5) |
Proof.Consider a point  There are points on
There are points on 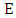 with
with  coodinate
coodinate 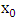 if
if 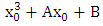 is a non-zero square in
is a non-zero square in 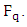 There is one such point if it is zero, and no such points if it is square It follows that the number of points in
There is one such point if it is zero, and no such points if it is square It follows that the number of points in 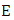 with
with 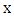 coordinate
coordinate 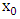 is
is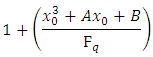 So to find the order of
So to find the order of 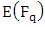 we must sum over all
we must sum over all 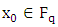 and add 1 for the point at infinity:
and add 1 for the point at infinity: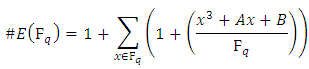
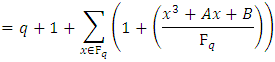
3.5. Example 5
Let  be the curve
be the curve 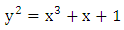 over
over 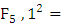
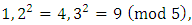
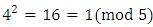 So the non-zero squares modulo 5 are 1 and 4.
So the non-zero squares modulo 5 are 1 and 4.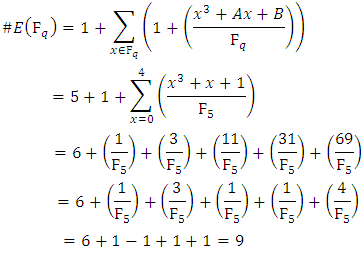
3.6. Theorem 3 (Hasse’s Theorem)
Let E be an elliptic curve over the finite field 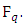 Then the order of
Then the order of 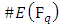 satisfies the following inequality.
satisfies the following inequality.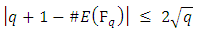
3.7. The Frobenius Endomorphism
The Frobenius Map is the function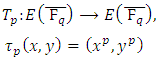 | (4) |
The quality 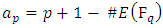 is called the Trace of Frobenius. [16]What are rational solutions? This question is even more difficult in general. If the degree of the equation is higher than three, little is known. If the degree is exactly three, we have essentially an elliptic curve. [17]
is called the Trace of Frobenius. [16]What are rational solutions? This question is even more difficult in general. If the degree of the equation is higher than three, little is known. If the degree is exactly three, we have essentially an elliptic curve. [17]
3.8. Theorem 4 (Henri Poincare’s Theorem, 1901)
Let 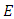 be an elliptic curve defined over a field
be an elliptic curve defined over a field 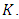 Then
Then  is an abelian group under +.
is an abelian group under +.
4. Conjecture 1 (Henri Poincare’s Conjecture, 1901)
Let 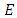 be an elliptic curve. Then
be an elliptic curve. Then 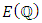 is finitely generated Mordell gave a good partial answer in 1923 (based on a conjecture of Henri Poincare in 1901), known as Mordell’s Theorem. This result states that the group
is finitely generated Mordell gave a good partial answer in 1923 (based on a conjecture of Henri Poincare in 1901), known as Mordell’s Theorem. This result states that the group 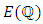 of rational points on an elliptic curve is "finitely generated". This means that, if there are any rational solutions, then they can all be determined from a certain finite subset of them.Unfortunately, there are two things that Mordell’s result does not do. First, it provides no way to tell whether any rational points exist (other than the "point at infinity"). Second, it does not provide an "effective" means (i.e. an algorithm) for finding a set of generators for the group of rational points. In some cases Mordell’s methods are able to do this. And it has been conjectured, but not yet proven, that the methods will work in all cases. There is a general theorem about finitely generated abelian groups such as
of rational points on an elliptic curve is "finitely generated". This means that, if there are any rational solutions, then they can all be determined from a certain finite subset of them.Unfortunately, there are two things that Mordell’s result does not do. First, it provides no way to tell whether any rational points exist (other than the "point at infinity"). Second, it does not provide an "effective" means (i.e. an algorithm) for finding a set of generators for the group of rational points. In some cases Mordell’s methods are able to do this. And it has been conjectured, but not yet proven, that the methods will work in all cases. There is a general theorem about finitely generated abelian groups such as 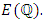 It states that any finitely generated abelian group is the "direct sum" of the subgroup consisting of elements of finite order and zero or more copies of the additive group
It states that any finitely generated abelian group is the "direct sum" of the subgroup consisting of elements of finite order and zero or more copies of the additive group 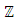 of integers. [14]
of integers. [14]
4.1. Theorem 5 (Mordell Theorem)
If E is an elliptic curve over 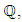 then the commutative group
then the commutative group 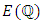 is finitely generated.By Mordell’s theorem we can write
is finitely generated.By Mordell’s theorem we can write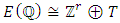 Where
Where 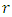 is a nonnegative integer and
is a nonnegative integer and 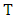 is the Torsion subgroup of elements of finite order in
is the Torsion subgroup of elements of finite order in 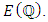 This subgroup is called the torsion subgroup of
This subgroup is called the torsion subgroup of 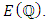 The integer
The integer 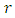 is called the rank of
is called the rank of 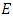 and is written
and is written 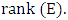 Determining
Determining 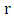 theoretically and in practice is currently the main problem of arithmetic elliptic curve theory. As it happens, much more is known about the torsion part of the group
theoretically and in practice is currently the main problem of arithmetic elliptic curve theory. As it happens, much more is known about the torsion part of the group 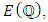 denoted by
denoted by 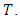 A theorem due to Elisabeth Lutz and Trygve Nagell in the 1930’s showed how to compute
A theorem due to Elisabeth Lutz and Trygve Nagell in the 1930’s showed how to compute 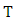 in any particular case. [1]
in any particular case. [1]
4.2. Torsion Subgroups
The torsion subgroup is "well-understood". First, there is an effective algorithm to determine 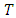 given
given 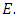
4.2.1. Theorem 6 (Nagell-Lutz)
Let 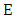 be the elliptic curve
be the elliptic curve 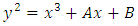 . If
. If 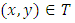 and Then
and Then 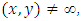 then1.
then1. 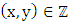 2. either
2. either 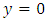 or
or 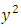 divides
divides 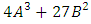
4.2.2. Corollary 1
Let  bean elliptic curve defined over
bean elliptic curve defined over 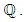 Then the torsion subgroup
Then the torsion subgroup 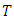 is finite.Proof: Suppose
is finite.Proof: Suppose 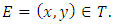 By Lutz-Nagell,
By Lutz-Nagell,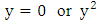 divides
divides 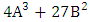 so there are only finitely many possibilities for
so there are only finitely many possibilities for 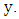 Fixing
Fixing 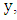 there are at most 3 solutions to
there are at most 3 solutions to  in
in  thus
thus 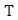 is finite group.
is finite group.
4.2.3. Example 6
Let 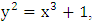 then Torsion subgroup
then Torsion subgroup 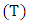 are1) (-1, 0) has order 22) (0,±1) has order 33) (2,±3) has order 6
are1) (-1, 0) has order 22) (0,±1) has order 33) (2,±3) has order 6
4.2.4. Theorem 7 (Mazur Theorem)
If E is an elliptic curve, then T is one of the following 15 groups: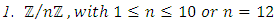
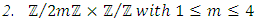
 | Figure 3. Examples of torsion subgroups of elliptic curves [9] |
Each of the groups in Theorem 6 occurs infinitely often as the torsion subgroup of an elliptic curve over 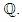
4.3. Ranks
The rank of an elliptic curve is a measure of the size of the set of rational points. There is no analogue of Theorems 12 or 14 for ranks:Ÿ there is no known algorithm guaranteed to determine rank of  Ÿ it is not known exactly which integers can occur as the rank of an elliptic curve. [1]
Ÿ it is not known exactly which integers can occur as the rank of an elliptic curve. [1]
4.4. Reduction of an Elliptic Curve Modulo p
Let 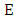 be an elliptic curve given by an equation
be an elliptic curve given by an equation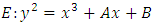 with
with 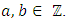 We can reduce the coefficients of
We can reduce the coefficients of 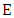 modulo a prime
modulo a prime  to get an elliptic curve
to get an elliptic curve 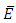 with coefficients in
with coefficients in 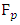
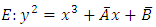 With
With 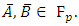 However, remember we must check that
However, remember we must check that 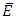 is not singular, which means that we need the discriminant
is not singular, which means that we need the discriminant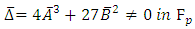 We say that E has Good Reduction at p if p does not divide the discriminant
We say that E has Good Reduction at p if p does not divide the discriminant 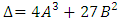 and we say that
and we say that 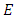 has Bad Reduction at
has Bad Reduction at 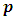 if p does divide the discriminant.
if p does divide the discriminant.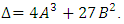 When we talk about reduction modulo
When we talk about reduction modulo 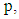 we will generally assume that we have good reduction at
we will generally assume that we have good reduction at 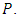 [13]
[13]
4.5. The Reduction Modulo p Homomorphism
It is hard to overstate the importance of reduction modulo p. A first indication is:
4.6. Theorem 8
If 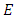 has good reduction, then the reduction modulo
has good reduction, then the reduction modulo 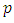 map
map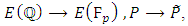 is a group homomorphism.
is a group homomorphism.
4.7. Example 6
Let 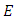 be the elliptic curve
be the elliptic curve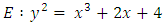 Some points in are
Some points in are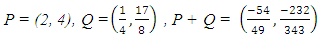 The reduction modulo 11 map
The reduction modulo 11 map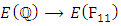
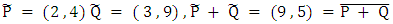
5. The Birch and Swinnerton-Dyer Conjecture
Fix an elliptic curve 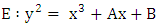 over
over  For every prime number
For every prime number  not dividing the discriminant.
not dividing the discriminant.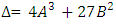 of
of 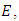 we can reduce
we can reduce 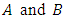 modulo
modulo 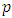 and view
and view  as an elliptic curve over the finite field
as an elliptic curve over the finite field 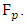 Reduction modulo
Reduction modulo 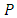 induces a group homomorphism.
induces a group homomorphism. 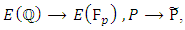 The idea of Birch and Swinnerton-Dyer was that the large
The idea of Birch and Swinnerton-Dyer was that the large 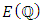 is, the larger
is, the larger 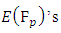 should be "on average" as
should be "on average" as 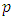 varies. The size of can be measured by rank of
varies. The size of can be measured by rank of 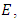 but how can one measure the average size of the
but how can one measure the average size of the  [1]
[1]
5.1. What does 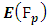 look like?
look like?
The group 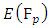 is obviously a finite group. Indeed, it clearly has no more than
is obviously a finite group. Indeed, it clearly has no more than 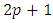 points. For each
points. For each 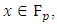 there is a "50% chance" that the value of
there is a "50% chance" that the value of 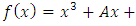
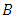 is a square in
is a square in 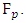 And if
And if 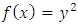 is a square, then we (usually) get two points
is a square, then we (usually) get two points  in
in 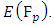 Plus there’s the point at infinity
Plus there’s the point at infinity  Thus we might expect to contain approximately [13]
Thus we might expect to contain approximately [13]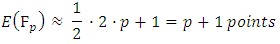 A famous theorem of Hasse makes this precise.
A famous theorem of Hasse makes this precise.
5.2. Theorem 9 (Hasse’s Theorem)
Let 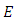 be an elliptic curve
be an elliptic curve 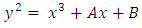 with
with 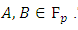 Then
Then For every prime number p not dividing
For every prime number p not dividing  Let
Let 
5.2.1. Numerical experiments of the Birch and Swinnerton-Dyer
To test their idea, in the 1950’s Birch and Swinnerton-Dyer computed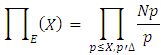 as
as 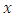 grows, for certain elliptic curves
grows, for certain elliptic curves 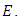 Figure 2 shows the behaviour of
Figure 2 shows the behaviour of 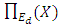 for
for 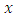 up to about
up to about 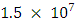 for five different curves
for five different curves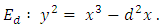 The horizontal axis is
The horizontal axis is  and the vertical axis is
and the vertical axis is 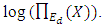 From their data Birch and Swinnerton-Dyer were led to conjecture that
From their data Birch and Swinnerton-Dyer were led to conjecture that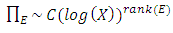 | (5) |
As 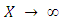 for some constant
for some constant 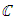 depending only on
depending only on 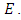 (Note that this relation is consistent with the data in Figure 2. if the axes were to scale, then the slopes of the lines would be the ranks of the curves.) The function
(Note that this relation is consistent with the data in Figure 2. if the axes were to scale, then the slopes of the lines would be the ranks of the curves.) The function 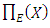 does not behave very nicely and therefore is difficult to work with. Birch and Swinnerton-Dyer stated a related conjecture, using the L-function of E in place of
does not behave very nicely and therefore is difficult to work with. Birch and Swinnerton-Dyer stated a related conjecture, using the L-function of E in place of 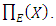 [1]
[1]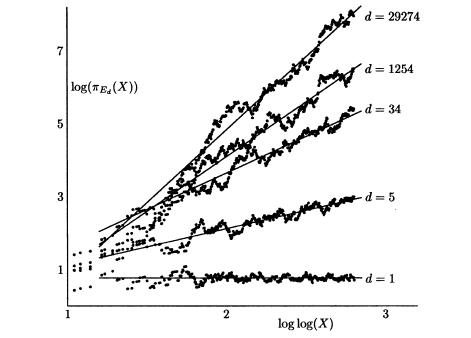 | Figure 4. Birch and swinnerton-Dyer data for 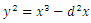 |
5.3. The L-Series of an Elliptic Curve
Let 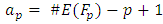 Analogous to the Euler factors of the Riemann zeta function, we define the local L-factor of E to be
Analogous to the Euler factors of the Riemann zeta function, we define the local L-factor of E to be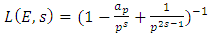 | (6) |
The variable s is a complex variable 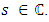 When evaluating its value at
When evaluating its value at 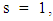 we retrieve the arithmetic information at
we retrieve the arithmetic information at 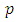
 | (7) |
Notice that each point in 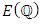 reduces to a point in
reduces to a point in 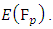 So when
So when 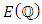 then
then 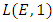 tends to be small. Birch and Swinnerton-Dyer observed that if
tends to be small. Birch and Swinnerton-Dyer observed that if 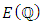 is infinite, then the reduction of the points in
is infinite, then the reduction of the points in  tend to make
tend to make 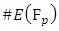 large than usual. So they conjectured Birch and Swinnerton-Dyer did numerical experiments and suggested
large than usual. So they conjectured Birch and Swinnerton-Dyer did numerical experiments and suggested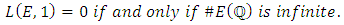 The L-function of
The L-function of 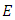 is defined to be the product of all local
is defined to be the product of all local 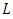
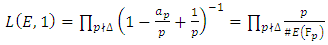 | (8) |
So intuitively the rank of 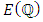 will correspond to the value of L(E, s) at s=1: the larger r is, the "smaller" L(E, 1) is. However, the value of L (E, s) at s = 1 does not make sense since the product of L (E, s) only converges when R(s) > 3/2.Nevertheless, if L(E, s) can be continued to an analytic function on the whole of
will correspond to the value of L(E, s) at s=1: the larger r is, the "smaller" L(E, 1) is. However, the value of L (E, s) at s = 1 does not make sense since the product of L (E, s) only converges when R(s) > 3/2.Nevertheless, if L(E, s) can be continued to an analytic function on the whole of 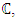 it may be reasonable to believe that the behavior of L(E, s) at s = 1 contains the arithmetic information of the rank of
it may be reasonable to believe that the behavior of L(E, s) at s = 1 contains the arithmetic information of the rank of 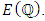 A deep theorem of Wiles et al., which many consider the crowning achievement of 1990s number theory, implies that L(E, s) can be analytically continued to an analytic function on all
A deep theorem of Wiles et al., which many consider the crowning achievement of 1990s number theory, implies that L(E, s) can be analytically continued to an analytic function on all 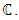 This implies that L(E, s) has a Taylor series expansion about s = 1. [12]
This implies that L(E, s) has a Taylor series expansion about s = 1. [12]
5.4. Theorem 10 (Wiles’ Theorem)
The function L(E, s) extends to an analytic function on all of 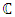 and satisfies a function equation
and satisfies a function equation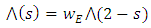 | (9) |
where 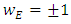 and
and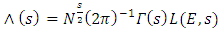 | (10) |
for some positive 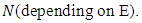
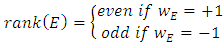 Where
Where 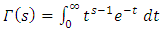
5.5. Taylor expansion of L(E,s) about s = 1
 with
with  the analytic rank
the analytic rank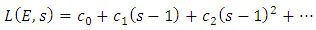 Define the analytic rank
Define the analytic rank  of E to be the order of vanishing of L (E, s) as s = 1. [5]The famous Birch and Swinnerton-Dyer conjecture asserts that Birch and Swinnerton-Dyer conjecture.
of E to be the order of vanishing of L (E, s) as s = 1. [5]The famous Birch and Swinnerton-Dyer conjecture asserts that Birch and Swinnerton-Dyer conjecture.
5.6. Conjecture 1
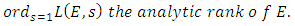 The Birch and Swinnerton-Dyer Conjecture can then be stated simply as: for any elliptic curve
The Birch and Swinnerton-Dyer Conjecture can then be stated simply as: for any elliptic curve 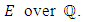 Then the algebraic and analytic ranks of E are the same. Goldfeld also proved the following surprising result, which says in particular that, the connection between
Then the algebraic and analytic ranks of E are the same. Goldfeld also proved the following surprising result, which says in particular that, the connection between  and
and 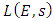 is off by a factor of
is off by a factor of 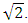 [17]
[17]
5.7. Theorem 11. (Goldfled Theorem)
Suppose  where
where  with constants
with constants  and
and 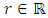 . Then
. Then 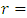
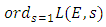 and
and 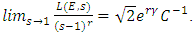 Where
Where  Euler’s constant. In particular, if r = 0 then
Euler’s constant. In particular, if r = 0 then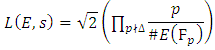 The lines
The lines  figure 2 were calculated using equation 5, Theorem 11, and the full Birch and Swinnerton-Dyer Conjecture to determine
figure 2 were calculated using equation 5, Theorem 11, and the full Birch and Swinnerton-Dyer Conjecture to determine 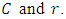
5.8. Theorem 12
Suppose 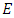 is an elliptic curve over
is an elliptic curve over 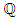 and that
and that 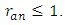 Then the algebraic and analytic ranks of E are the same.A quote from William A. Stein:In 2000, Conjecture 1 was declared a million dollar millennium prize problem by the Clay Mathematics Institute, which motivated even more work, conferences, etc., on the conjecture. Since then, to the best of my knowledge, not a single new result directly about Conjecture 1 has been proved. The class of curves for which we know the conjecture is still the set of curves over
Then the algebraic and analytic ranks of E are the same.A quote from William A. Stein:In 2000, Conjecture 1 was declared a million dollar millennium prize problem by the Clay Mathematics Institute, which motivated even more work, conferences, etc., on the conjecture. Since then, to the best of my knowledge, not a single new result directly about Conjecture 1 has been proved. The class of curves for which we know the conjecture is still the set of curves over  with
with 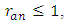 along with a finite set of individual curves on which further computer calculations have been performed (by Cremona, Watkins, myself, and others)."A new idea is needed".Nick Katz on BSD, at a 2001 Arizona Winter School.The following theorem, a combination of work of Kolyvagin, Gross and Zagier, and others, is the best result to date in the direction of the Birch and Swinnerton-Dyer Conjecture. [17]
along with a finite set of individual curves on which further computer calculations have been performed (by Cremona, Watkins, myself, and others)."A new idea is needed".Nick Katz on BSD, at a 2001 Arizona Winter School.The following theorem, a combination of work of Kolyvagin, Gross and Zagier, and others, is the best result to date in the direction of the Birch and Swinnerton-Dyer Conjecture. [17]
5.9. Theorem 13 (Gross-Zagier, Kolyvagin Theorem)
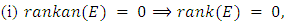
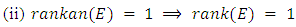 Assertion (i) can be rephrase as
Assertion (i) can be rephrase as 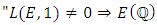 is finite”Assertion (ii) can be rephrase as
is finite”Assertion (ii) can be rephrase as 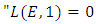 and
and 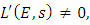 then r = 1, and there is an efficient method for calculating
then r = 1, and there is an efficient method for calculating 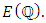 The case
The case 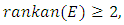 remains completely open problem.
remains completely open problem.
5.9.1. Example 23
If 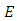 is the curve
is the curve  then
then 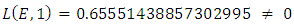 Thus theorem 22 (i) shows that
Thus theorem 22 (i) shows that 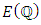 is finite.The sign
is finite.The sign 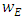 in the functional equation for
in the functional equation for 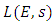 determines the parity of
determines the parity of 
 The Birch and Swinnerton-Dyer Conjecture predicts in particular that rank(E) and rankan(E) have the same parity, so the following is a consequence of the Birch and Swinnerton-Dyer Conjecture.
The Birch and Swinnerton-Dyer Conjecture predicts in particular that rank(E) and rankan(E) have the same parity, so the following is a consequence of the Birch and Swinnerton-Dyer Conjecture.
5.10. Conjecture 2. (Parity Conjecture)
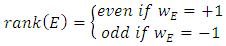 To explain the recent progress concerning the Parity Conjecture, we need to introduce the Tate-Shafarevich group and the Selmer group. The Tate-Shafarevich group
To explain the recent progress concerning the Parity Conjecture, we need to introduce the Tate-Shafarevich group and the Selmer group. The Tate-Shafarevich group 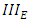 is a torsion group that measures the failure of the Hasse’s Principle for curves that is principal homogeneous spaces for
is a torsion group that measures the failure of the Hasse’s Principle for curves that is principal homogeneous spaces for 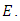
5.11. Conjecture 3 (Birch and Swinnerton-Dyer)
Let 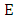 be an elliptic curve over
be an elliptic curve over  of rank
of rank 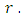 Then
Then 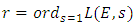 and
and And another quote from Bertolini-Darmon (2001):"The following question stands as the ultimate challenge concerning the Birch and Swinnerton-Dyer conjecture for elliptic curves over
And another quote from Bertolini-Darmon (2001):"The following question stands as the ultimate challenge concerning the Birch and Swinnerton-Dyer conjecture for elliptic curves over 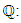 Provide evidence for the Birch and Swinnerton-Dyer conjecture in cases where
Provide evidence for the Birch and Swinnerton-Dyer conjecture in cases where 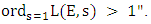 [17]
[17]
6. Conclusions
In conclusion, although there has been little success in the last fifty years in finding the number of rational points on an elliptic curve, there are still almost no methods for finding such points. It is to be hoped that a proof of the Birch and Swinnerton-Dyer conjecture will give some insight on the number of rational points on an elliptic curve.
ACKNOWLEDGEMENTS
The authors thank the staff at the Mathematics Department of Kwame Nkrumah University of Science and Technology for their support and kindness during the period this paper was written.
References
| [1] | R. Karl and S. Alice. Rank of Elliptic Curves. American Mathematical Society Pages 455474 S 0273-0979(02) 00952-7, 2002, Vol.39, No.4. http://dx.doi.org/10.1090/s0273-0979-02-00952-7. |
| [2] | J. H. Silverman. The Arithmetic of Elliptic Curves. New York: Springer, 2009. Print. http://dx.doi.org/10.1007/978-0-387-09494-6. |
| [3] | J. Coates, A. Wiles. On the conjecture of Birch and Swinnerton-Dyer. Swinnerton-Dyer, Invent. Math. 1977, 39, 223-251 http://dx.doi.org/10.1007/bf01402975. |
| [4] | B. Gross, D. Zagier .Heegner Points and Derivatives of L-series. n vent. Math. 84, 1986, pp. 225-320 http://dx.doi.org/10.1007/bf01388809. |
| [5] | J. Cremona. Algorithms for Modular Elliptic Curves, Cambridge: Cambridge University Press. 1992 http://dx.doi.org/10.2307/3618360 |
| [6] | L. Washington. Number Theory and Cryptography. Chapman and Hall/CRC, 2003. An introduction to elliptic curves and ECC at an advanced undergraduate/beginning graduate level. http://dx.doi.org/10.5860/choice.41-4097. |
| [7] | J. Conway. Functions of One Complex Variable I. Springer, 1986. ISBN 0-387-90328-3. http://dx.doi.org/10.1007/978-1-4612-6313-5. |
| [8] | Alozano, Examples of torsion subgroups of elliptic curves [Online]. Available: 2013-02-02. From http:// www.planetmath.org. |
| [9] | A. Wiles, the Birch and Swinnerton-Dyer conjecture. [Online]. Available http://www.claymath.org/prize problems/birchsd.htm. |
| [10] | J. B. Fraleigh. A first course in abstract algebra. 5th edition, Addison- Wesley. 1994 http://dx.doi.org/10.2307/3617251. |
| [11] | J. H. Silverman. The arithmetic of elliptic curves. Graduate Texts in Mathematics, 106.Springer-Verlag, New York, 1986. [The number theory of elliptic curves at a level suitable for advanced graduate students.]. http://dx.doi.org/10.1007/978-1-4757-1920-8. |
| [12] | M. England, Elliptic curve cryptography. Heriot-Watt University. Summer 2006. |
| [13] | J. H. Silverman, An Introduction to the Theory of Elliptic Curves. Summer School on Computational Number Theory and Applications to Cryptography University of Wyoming June 19 -July 7. |
| [14] | C. Daney.Elliptic Curves and Modular Forms. Retrieved 2015-01-13 from http://www.openquestions.com/oq-main.htm,2002. |
| [15] | Z. DeStefano,. 2010. On the Torsion Subgroup of an Elliptic Curve Retrieved 2015-02-13 from http://www math.nyu.edu/degree/undergrad/ug research/presentation2.pdf, S.U.R.E Presentation. |
| [16] | E. H. Goins, Why Should I Care About Elliptic Curves Department of Mathematics, Purdue University MAA Math Fest, and Retrieved 2015-01-13 from http://www.math.buffalo.edu/mad/PEEPS/blackwell david.htlm. |
| [17] | W. Stein. The Birch and Swinnerton-Dyer Conjecture, a Computational Approach. Retrieved 2015-01-13 from http://www.wstein.org/books/modform/stein-modform.pdf. |



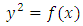
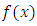 has no multiple roots. The cubic equation
has no multiple roots. The cubic equation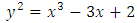 does not define an elliptic curve, because
does not define an elliptic curve, because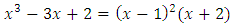 has 1 as a multiple root. Similarly
has 1 as a multiple root. Similarly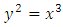 is not an elliptic curve, but
is not an elliptic curve, but is an elliptic curve.The general form of an elliptic curve is given below
is an elliptic curve.The general form of an elliptic curve is given below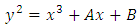
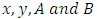 belong to a specified field such as
belong to a specified field such as 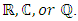 General we use
General we use 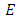 to represent an elliptic curve. If we wish to consider points in a field
to represent an elliptic curve. If we wish to consider points in a field 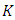 we write
we write 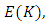 which is defined as below.
which is defined as below.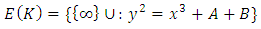
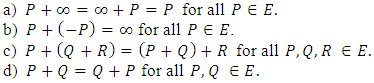 In other words, the addition law + makes the points of E into a commutative group. [11]
In other words, the addition law + makes the points of E into a commutative group. [11]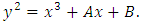 Let
Let 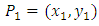 and
and  be points on
be points on 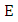 with
with 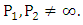 We the define
We the define 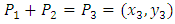 as follows 1. If
as follows 1. If 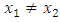 then
then 
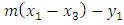 where
where 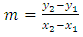 .2. If
.2. If 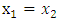 but
but  then
then 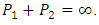 3. If
3. If 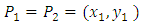 and
and 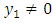 then
then 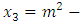
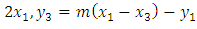 where
where 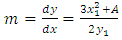 .4. If
.4. If 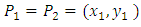 and
and 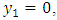 then
then 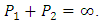 Also we define
Also we define 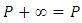 for all points
for all points 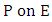 [12].
[12].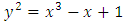 and suppose we know the point
and suppose we know the point 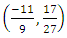 and
and 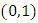 lies on the curve. To find another point on. In the notation of elliptic curve addition we have:
lies on the curve. To find another point on. In the notation of elliptic curve addition we have: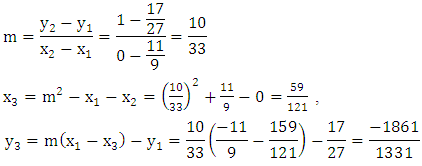

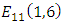 is the set of integers
is the set of integers 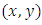 that satisfy
that satisfy 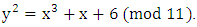 We can see that
We can see that 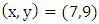 is the set as
is the set as 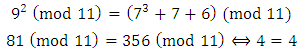 To find all the points in
To find all the points in 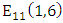 we find all the possible values
we find all the possible values 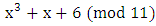 and then see what values of
and then see what values of 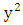 will match. There are 11 choices of
will match. There are 11 choices of  the integers
the integers  Subbing these values in turn into the cubic and reducing modulo 11 will give us the possible values of
Subbing these values in turn into the cubic and reducing modulo 11 will give us the possible values of 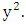
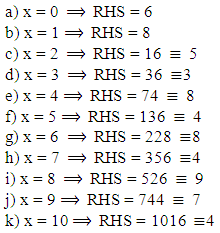 So we can see that the possible values of
So we can see that the possible values of  cannot be 0, 1, 2 or 10.Next examine the 10 possible values of
cannot be 0, 1, 2 or 10.Next examine the 10 possible values of 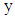 and identify which values of
and identify which values of  they could be paired with to give a point on the curve.
they could be paired with to give a point on the curve.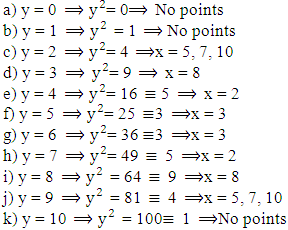
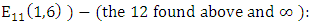
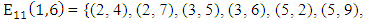
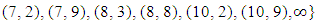
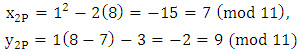 So in
So in  we find
we find 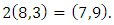
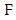 be a finite field and
be a finite field and 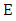 an elliptic curve defined over
an elliptic curve defined over  Since there are only a finite number of pairs
Since there are only a finite number of pairs 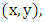 with
with 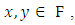 the group
the group 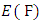 must itself be finite. In this section. We discuss the basic theory of elliptic curves over finite fields and also we will state Hasse’s theorem which gives a bound of the size of the group defined by
must itself be finite. In this section. We discuss the basic theory of elliptic curves over finite fields and also we will state Hasse’s theorem which gives a bound of the size of the group defined by 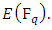 We also look at methods to find the order of a point in
We also look at methods to find the order of a point in  [12].
[12].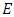 be thr curve
be thr curve 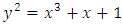 over
over 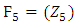
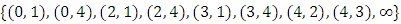
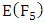 has order 9.
has order 9. 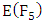 is cyclic and generated by (0,1).
is cyclic and generated by (0,1).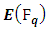
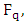 we can determine the order of
we can determine the order of 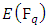 by listing the points. We can then determine the order of
by listing the points. We can then determine the order of 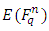 for all
for all 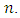 [12]
[12]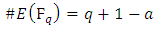 write
write 
 then for all
then for all 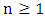
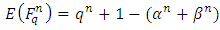
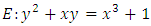 be an elliptic curve
be an elliptic curve 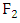 satisfies
satisfies 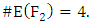 Therefore
Therefore 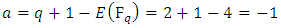 and we obtain the polynomial
and we obtain the polynomial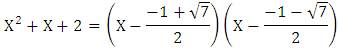
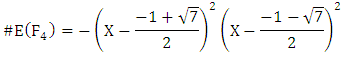 We could compute the last expression directly, but better use the recurrence relation
We could compute the last expression directly, but better use the recurrence relation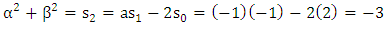 So,
So, 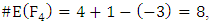 (as we calculated when listing points).
(as we calculated when listing points).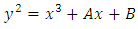 over a finite field, we listed every possible value of
over a finite field, we listed every possible value of 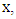 and then found the square roots,
and then found the square roots,  of
of 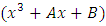 if they existed. This procedure will be the basis for a simple point counting algorithm.The Legendre symbol we can generalize this to a finite field
if they existed. This procedure will be the basis for a simple point counting algorithm.The Legendre symbol we can generalize this to a finite field 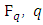 odd, by defining for
odd, by defining for 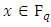
 We can now give a more accurate solution to the number of points on
We can now give a more accurate solution to the number of points on 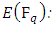
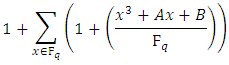
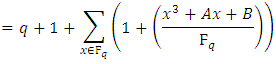
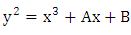 over
over  Then
Then 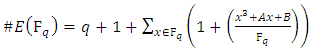
 There are points on
There are points on  with
with  coodinate
coodinate 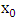 if
if 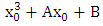 is a non-zero square in
is a non-zero square in 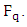 There is one such point if it is zero, and no such points if it is square It follows that the number of points in
There is one such point if it is zero, and no such points if it is square It follows that the number of points in 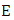 with
with 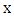 coordinate
coordinate 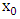 is
is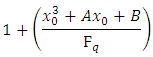 So to find the order of
So to find the order of 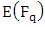 we must sum over all
we must sum over all 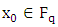 and add 1 for the point at infinity:
and add 1 for the point at infinity: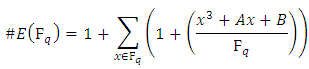
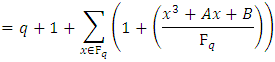
 be the curve
be the curve 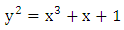 over
over 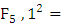
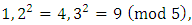
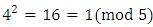 So the non-zero squares modulo 5 are 1 and 4.
So the non-zero squares modulo 5 are 1 and 4.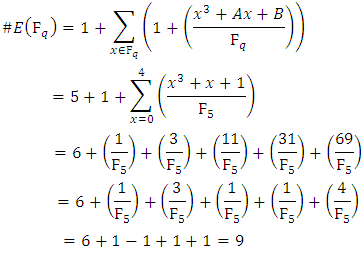
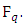 Then the order of
Then the order of 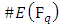 satisfies the following inequality.
satisfies the following inequality.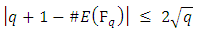
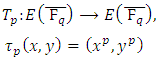
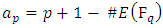 is called the Trace of Frobenius. [16]What are rational solutions? This question is even more difficult in general. If the degree of the equation is higher than three, little is known. If the degree is exactly three, we have essentially an elliptic curve. [17]
is called the Trace of Frobenius. [16]What are rational solutions? This question is even more difficult in general. If the degree of the equation is higher than three, little is known. If the degree is exactly three, we have essentially an elliptic curve. [17]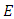 be an elliptic curve defined over a field
be an elliptic curve defined over a field 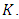 Then
Then  is an abelian group under +.
is an abelian group under +.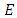 be an elliptic curve. Then
be an elliptic curve. Then 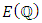 is finitely generated Mordell gave a good partial answer in 1923 (based on a conjecture of Henri Poincare in 1901), known as Mordell’s Theorem. This result states that the group
is finitely generated Mordell gave a good partial answer in 1923 (based on a conjecture of Henri Poincare in 1901), known as Mordell’s Theorem. This result states that the group 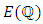 of rational points on an elliptic curve is "finitely generated". This means that, if there are any rational solutions, then they can all be determined from a certain finite subset of them.Unfortunately, there are two things that Mordell’s result does not do. First, it provides no way to tell whether any rational points exist (other than the "point at infinity"). Second, it does not provide an "effective" means (i.e. an algorithm) for finding a set of generators for the group of rational points. In some cases Mordell’s methods are able to do this. And it has been conjectured, but not yet proven, that the methods will work in all cases. There is a general theorem about finitely generated abelian groups such as
of rational points on an elliptic curve is "finitely generated". This means that, if there are any rational solutions, then they can all be determined from a certain finite subset of them.Unfortunately, there are two things that Mordell’s result does not do. First, it provides no way to tell whether any rational points exist (other than the "point at infinity"). Second, it does not provide an "effective" means (i.e. an algorithm) for finding a set of generators for the group of rational points. In some cases Mordell’s methods are able to do this. And it has been conjectured, but not yet proven, that the methods will work in all cases. There is a general theorem about finitely generated abelian groups such as 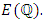 It states that any finitely generated abelian group is the "direct sum" of the subgroup consisting of elements of finite order and zero or more copies of the additive group
It states that any finitely generated abelian group is the "direct sum" of the subgroup consisting of elements of finite order and zero or more copies of the additive group 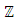 of integers. [14]
of integers. [14]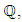 then the commutative group
then the commutative group 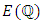 is finitely generated.By Mordell’s theorem we can write
is finitely generated.By Mordell’s theorem we can write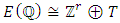 Where
Where 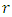 is a nonnegative integer and
is a nonnegative integer and 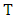 is the Torsion subgroup of elements of finite order in
is the Torsion subgroup of elements of finite order in 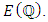 This subgroup is called the torsion subgroup of
This subgroup is called the torsion subgroup of 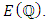 The integer
The integer 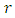 is called the rank of
is called the rank of 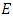 and is written
and is written 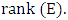 Determining
Determining 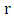 theoretically and in practice is currently the main problem of arithmetic elliptic curve theory. As it happens, much more is known about the torsion part of the group
theoretically and in practice is currently the main problem of arithmetic elliptic curve theory. As it happens, much more is known about the torsion part of the group 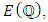 denoted by
denoted by 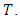 A theorem due to Elisabeth Lutz and Trygve Nagell in the 1930’s showed how to compute
A theorem due to Elisabeth Lutz and Trygve Nagell in the 1930’s showed how to compute 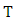 in any particular case. [1]
in any particular case. [1]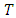 given
given 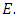
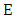 be the elliptic curve
be the elliptic curve 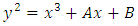 . If
. If 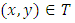 and Then
and Then  then1.
then1. 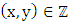 2. either
2. either 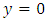 or
or 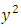 divides
divides 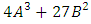
 bean elliptic curve defined over
bean elliptic curve defined over  Then the torsion subgroup
Then the torsion subgroup 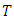 is finite.Proof: Suppose
is finite.Proof: Suppose 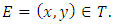 By Lutz-Nagell,
By Lutz-Nagell,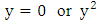 divides
divides 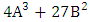 so there are only finitely many possibilities for
so there are only finitely many possibilities for 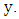 Fixing
Fixing 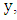 there are at most 3 solutions to
there are at most 3 solutions to  in
in  thus
thus 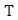 is finite group.
is finite group. 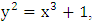 then Torsion subgroup
then Torsion subgroup  are1) (-1, 0) has order 22) (0,±1) has order 33) (2,±3) has order 6
are1) (-1, 0) has order 22) (0,±1) has order 33) (2,±3) has order 6

 Ÿ it is not known exactly which integers can occur as the rank of an elliptic curve. [1]
Ÿ it is not known exactly which integers can occur as the rank of an elliptic curve. [1] be an elliptic curve given by an equation
be an elliptic curve given by an equation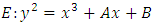 with
with 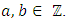 We can reduce the coefficients of
We can reduce the coefficients of 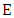 modulo a prime
modulo a prime  to get an elliptic curve
to get an elliptic curve 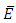 with coefficients in
with coefficients in 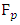
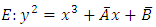 With
With 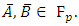 However, remember we must check that
However, remember we must check that 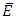 is not singular, which means that we need the discriminant
is not singular, which means that we need the discriminant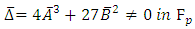 We say that E has Good Reduction at p if p does not divide the discriminant
We say that E has Good Reduction at p if p does not divide the discriminant 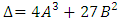 and we say that
and we say that 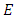 has Bad Reduction at
has Bad Reduction at 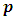 if p does divide the discriminant.
if p does divide the discriminant.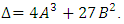 When we talk about reduction modulo
When we talk about reduction modulo 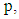 we will generally assume that we have good reduction at
we will generally assume that we have good reduction at 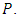 [13]
[13]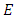 has good reduction, then the reduction modulo
has good reduction, then the reduction modulo 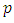 map
map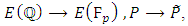 is a group homomorphism.
is a group homomorphism.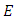 be the elliptic curve
be the elliptic curve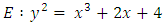 Some points in are
Some points in are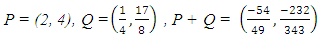 The reduction modulo 11 map
The reduction modulo 11 map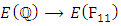
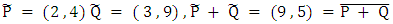
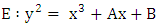 over
over 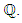 For every prime number
For every prime number 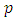 not dividing the discriminant.
not dividing the discriminant.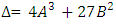 of
of 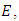 we can reduce
we can reduce 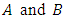 modulo
modulo 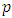 and view
and view  as an elliptic curve over the finite field
as an elliptic curve over the finite field 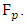 Reduction modulo
Reduction modulo 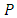 induces a group homomorphism.
induces a group homomorphism. 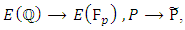 The idea of Birch and Swinnerton-Dyer was that the large
The idea of Birch and Swinnerton-Dyer was that the large 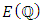 is, the larger
is, the larger 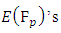 should be "on average" as
should be "on average" as 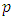 varies. The size of can be measured by rank of
varies. The size of can be measured by rank of 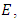 but how can one measure the average size of the
but how can one measure the average size of the  [1]
[1]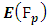 look like?
look like?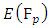 is obviously a finite group. Indeed, it clearly has no more than
is obviously a finite group. Indeed, it clearly has no more than 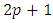 points. For each
points. For each 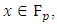 there is a "50% chance" that the value of
there is a "50% chance" that the value of 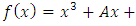
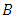 is a square in
is a square in 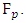 And if
And if 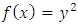 is a square, then we (usually) get two points
is a square, then we (usually) get two points  in
in 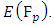 Plus there’s the point at infinity
Plus there’s the point at infinity  Thus we might expect to contain approximately [13]
Thus we might expect to contain approximately [13]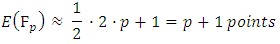 A famous theorem of Hasse makes this precise.
A famous theorem of Hasse makes this precise.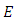 be an elliptic curve
be an elliptic curve 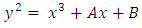 with
with 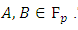 Then
Then For every prime number p not dividing
For every prime number p not dividing  Let
Let 
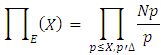 as
as 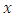 grows, for certain elliptic curves
grows, for certain elliptic curves 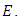 Figure 2 shows the behaviour of
Figure 2 shows the behaviour of 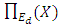 for
for 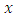 up to about
up to about 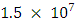 for five different curves
for five different curves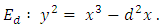 The horizontal axis is
The horizontal axis is 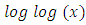 and the vertical axis is
and the vertical axis is 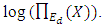 From their data Birch and Swinnerton-Dyer were led to conjecture that
From their data Birch and Swinnerton-Dyer were led to conjecture that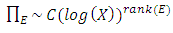
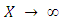 for some constant
for some constant 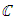 depending only on
depending only on 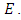 (Note that this relation is consistent with the data in Figure 2. if the axes were to scale, then the slopes of the lines would be the ranks of the curves.) The function
(Note that this relation is consistent with the data in Figure 2. if the axes were to scale, then the slopes of the lines would be the ranks of the curves.) The function 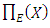 does not behave very nicely and therefore is difficult to work with. Birch and Swinnerton-Dyer stated a related conjecture, using the L-function of E in place of
does not behave very nicely and therefore is difficult to work with. Birch and Swinnerton-Dyer stated a related conjecture, using the L-function of E in place of 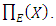 [1]
[1]
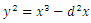
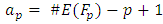 Analogous to the Euler factors of the Riemann zeta function, we define the local L-factor of E to be
Analogous to the Euler factors of the Riemann zeta function, we define the local L-factor of E to be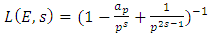
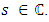 When evaluating its value at
When evaluating its value at 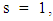 we retrieve the arithmetic information at
we retrieve the arithmetic information at 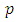

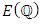 reduces to a point in
reduces to a point in 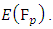 So when
So when 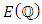 then
then 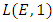 tends to be small. Birch and Swinnerton-Dyer observed that if
tends to be small. Birch and Swinnerton-Dyer observed that if 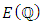 is infinite, then the reduction of the points in
is infinite, then the reduction of the points in  tend to make
tend to make 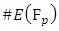 large than usual. So they conjectured Birch and Swinnerton-Dyer did numerical experiments and suggested
large than usual. So they conjectured Birch and Swinnerton-Dyer did numerical experiments and suggested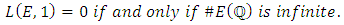 The L-function of
The L-function of 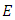 is defined to be the product of all local
is defined to be the product of all local 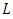
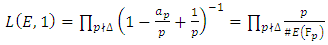
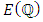 will correspond to the value of L(E, s) at s=1: the larger r is, the "smaller" L(E, 1) is. However, the value of L (E, s) at s = 1 does not make sense since the product of L (E, s) only converges when R(s) > 3/2.Nevertheless, if L(E, s) can be continued to an analytic function on the whole of
will correspond to the value of L(E, s) at s=1: the larger r is, the "smaller" L(E, 1) is. However, the value of L (E, s) at s = 1 does not make sense since the product of L (E, s) only converges when R(s) > 3/2.Nevertheless, if L(E, s) can be continued to an analytic function on the whole of 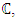 it may be reasonable to believe that the behavior of L(E, s) at s = 1 contains the arithmetic information of the rank of
it may be reasonable to believe that the behavior of L(E, s) at s = 1 contains the arithmetic information of the rank of 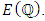 A deep theorem of Wiles et al., which many consider the crowning achievement of 1990s number theory, implies that L(E, s) can be analytically continued to an analytic function on all
A deep theorem of Wiles et al., which many consider the crowning achievement of 1990s number theory, implies that L(E, s) can be analytically continued to an analytic function on all 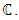 This implies that L(E, s) has a Taylor series expansion about s = 1. [12]
This implies that L(E, s) has a Taylor series expansion about s = 1. [12] and satisfies a function equation
and satisfies a function equation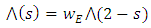
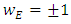 and
and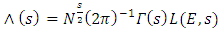
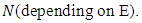
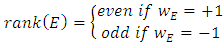 Where
Where 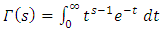
 with
with  the analytic rank
the analytic rank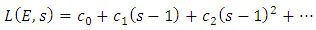 Define the analytic rank
Define the analytic rank 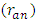 of E to be the order of vanishing of L (E, s) as s = 1. [5]The famous Birch and Swinnerton-Dyer conjecture asserts that Birch and Swinnerton-Dyer conjecture.
of E to be the order of vanishing of L (E, s) as s = 1. [5]The famous Birch and Swinnerton-Dyer conjecture asserts that Birch and Swinnerton-Dyer conjecture.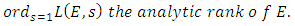 The Birch and Swinnerton-Dyer Conjecture can then be stated simply as: for any elliptic curve
The Birch and Swinnerton-Dyer Conjecture can then be stated simply as: for any elliptic curve 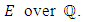 Then the algebraic and analytic ranks of E are the same. Goldfeld also proved the following surprising result, which says in particular that, the connection between
Then the algebraic and analytic ranks of E are the same. Goldfeld also proved the following surprising result, which says in particular that, the connection between  and
and 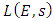 is off by a factor of
is off by a factor of 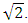 [17]
[17]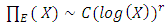 where
where 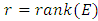 with constants
with constants 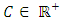 and
and 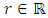 . Then
. Then 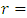
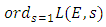 and
and 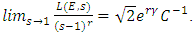 Where
Where  Euler’s constant. In particular, if r = 0 then
Euler’s constant. In particular, if r = 0 then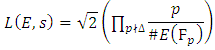 The lines
The lines  figure 2 were calculated using equation 5, Theorem 11, and the full Birch and Swinnerton-Dyer Conjecture to determine
figure 2 were calculated using equation 5, Theorem 11, and the full Birch and Swinnerton-Dyer Conjecture to determine 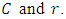
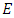 is an elliptic curve over
is an elliptic curve over  and that
and that 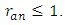 Then the algebraic and analytic ranks of E are the same.A quote from William A. Stein:In 2000, Conjecture 1 was declared a million dollar millennium prize problem by the Clay Mathematics Institute, which motivated even more work, conferences, etc., on the conjecture. Since then, to the best of my knowledge, not a single new result directly about Conjecture 1 has been proved. The class of curves for which we know the conjecture is still the set of curves over
Then the algebraic and analytic ranks of E are the same.A quote from William A. Stein:In 2000, Conjecture 1 was declared a million dollar millennium prize problem by the Clay Mathematics Institute, which motivated even more work, conferences, etc., on the conjecture. Since then, to the best of my knowledge, not a single new result directly about Conjecture 1 has been proved. The class of curves for which we know the conjecture is still the set of curves over  with
with 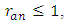 along with a finite set of individual curves on which further computer calculations have been performed (by Cremona, Watkins, myself, and others)."A new idea is needed".Nick Katz on BSD, at a 2001 Arizona Winter School.The following theorem, a combination of work of Kolyvagin, Gross and Zagier, and others, is the best result to date in the direction of the Birch and Swinnerton-Dyer Conjecture. [17]
along with a finite set of individual curves on which further computer calculations have been performed (by Cremona, Watkins, myself, and others)."A new idea is needed".Nick Katz on BSD, at a 2001 Arizona Winter School.The following theorem, a combination of work of Kolyvagin, Gross and Zagier, and others, is the best result to date in the direction of the Birch and Swinnerton-Dyer Conjecture. [17]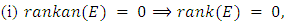
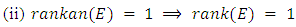 Assertion (i) can be rephrase as
Assertion (i) can be rephrase as 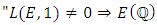 is finite”Assertion (ii) can be rephrase as
is finite”Assertion (ii) can be rephrase as 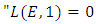 and
and 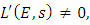 then r = 1, and there is an efficient method for calculating
then r = 1, and there is an efficient method for calculating 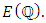 The case
The case 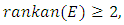 remains completely open problem.
remains completely open problem.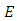 is the curve
is the curve  then
then 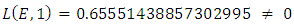 Thus theorem 22 (i) shows that
Thus theorem 22 (i) shows that 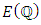 is finite.The sign
is finite.The sign 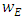 in the functional equation for
in the functional equation for 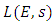 determines the parity of
determines the parity of 
 The Birch and Swinnerton-Dyer Conjecture predicts in particular that rank(E) and rankan(E) have the same parity, so the following is a consequence of the Birch and Swinnerton-Dyer Conjecture.
The Birch and Swinnerton-Dyer Conjecture predicts in particular that rank(E) and rankan(E) have the same parity, so the following is a consequence of the Birch and Swinnerton-Dyer Conjecture.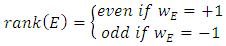 To explain the recent progress concerning the Parity Conjecture, we need to introduce the Tate-Shafarevich group and the Selmer group. The Tate-Shafarevich group
To explain the recent progress concerning the Parity Conjecture, we need to introduce the Tate-Shafarevich group and the Selmer group. The Tate-Shafarevich group  is a torsion group that measures the failure of the Hasse’s Principle for curves that is principal homogeneous spaces for
is a torsion group that measures the failure of the Hasse’s Principle for curves that is principal homogeneous spaces for 
 be an elliptic curve over
be an elliptic curve over 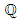 of rank
of rank 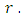 Then
Then 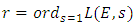 and
and And another quote from Bertolini-Darmon (2001):"The following question stands as the ultimate challenge concerning the Birch and Swinnerton-Dyer conjecture for elliptic curves over
And another quote from Bertolini-Darmon (2001):"The following question stands as the ultimate challenge concerning the Birch and Swinnerton-Dyer conjecture for elliptic curves over 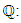 Provide evidence for the Birch and Swinnerton-Dyer conjecture in cases where
Provide evidence for the Birch and Swinnerton-Dyer conjecture in cases where 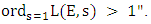 [17]
[17] Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML