Alkreemawi Walaa Khazal1, 2, Wang Xiang Jun1
1School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan, China
2Department of Mathematics, College of Science, Basra University, Basra, Iraq
Correspondence to: Alkreemawi Walaa Khazal, School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan, China.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
A stochastic differential equation (SDE) defines N independent stochastic processes The drift term depends on the random variable
The drift term depends on the random variable  . The distribution of the random effect
. The distribution of the random effect 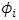 depends on unknown parameters, which are to be estimated from continuous observation of the processes
depends on unknown parameters, which are to be estimated from continuous observation of the processes 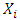 . When the drift term is defined linearly on the random effect
. When the drift term is defined linearly on the random effect 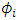 (additive random effect) and
(additive random effect) and 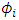 has a Gaussian mixture distribution, we obtain an expression of the exact likelihood. When the number of components is known, we prove the consistency of the maximum likelihood estimators
has a Gaussian mixture distribution, we obtain an expression of the exact likelihood. When the number of components is known, we prove the consistency of the maximum likelihood estimators 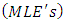 . The convergence of the EM algorithm described when the algorithm is used to compute
. The convergence of the EM algorithm described when the algorithm is used to compute 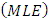 .
.
Keywords:
Maximum likelihood estimator, Mixed effects stochastic differential equations, Consistency, EM algorithm, Mixture distribution
Cite this paper: Alkreemawi Walaa Khazal, Wang Xiang Jun, Consistency of Estimators in Mixtures of Stochastic Differential Equations with Additive Random Effects, American Journal of Mathematics and Statistics, Vol. 6 No. 4, 2016, pp. 162-169. doi: 10.5923/j.ajms.20160604.04.
1. Introduction
A mixture model (MM) is beneficial for modeling data as output from one of several groups, clusters, or classes; the groups (clusters, classes) might be different from each other, but the observations within the same group are similar to each other. In this paper, we concentrate on the classification problem of longitudinal data modeled by a stochastic differential equation (SDE) with random effects that have a mixture of Gaussian distributions. Some researchers state that the classes are known, whereas other researchers state the opposite. Arribas-Gil et al. [1] and references therein assumed that the classes are known and deal with classification drawbacks of longitudinal data by using random effects models or mixed-effects models. Their aim is to establish a classification rule of longitudinal profiles (curves) into a number that enables dissimilar classes to predict the class of a new individual. Celeux et al. [6] and Delattre et al. [9] assumed that the numbers of classes are unknown. Celeux et al. [6] used maximum likelihood with the EM algorithm to estimate the random effects within a mixture of linear regression models that include random effects (see, Dempster, A. et. al. [10]), and they used Bayesian information criterion (BIC) to select the number of components. Delattreet al. [9] used maximum likelihood to estimate the random effects in SDE with multiplicative random effect in the drift and diffusion terms without random effects with the EM algorithm (Dempster, A. et. al. [10]). They also used BIC to select the number of components. Delattre et al. [9] studied SDEs with the following form: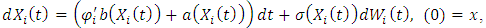 | (1) |
where  are
are 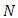 independent Wiener processes,
independent Wiener processes,  are
are 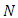 independently and identically distributed
independently and identically distributed  random variables. The processes
random variables. The processes 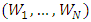 are also independent on random variables
are also independent on random variables 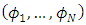 , and
, and 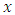 is a known real value. The drift function
is a known real value. The drift function 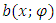 is a known function defined on
is a known function defined on  and the functions
and the functions 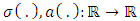 . Each process
. Each process  represents an individual, and the random variable
represents an individual, and the random variable  represents the random effect of individual i.Delattre et al. [2] considered the special case (multiple case) where
represents the random effect of individual i.Delattre et al. [2] considered the special case (multiple case) where 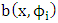 is linear in
is linear in 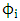 ; in other words,
; in other words,  , where
, where 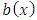 is a known real function, and
is a known real function, and 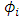 has a Gaussian mixture distribution.Here, we consider functional data modeled by a SDE with drift term
has a Gaussian mixture distribution.Here, we consider functional data modeled by a SDE with drift term 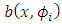 depending on random effects where
depending on random effects where  is linear in random effects
is linear in random effects  (addition case),
(addition case),  and diffusion term without random effects. We consider continuous observations
and diffusion term without random effects. We consider continuous observations 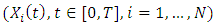 with a given
with a given 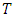 . Here,
. Here,  are unknown parameters in the distribution of
are unknown parameters in the distribution of  from the
from the 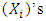 which will be estimated, but the estimation is not straightforward. Generally, the exact likelihood is not explicit. Maximum likelihood estimation in SDE with random effects has been studied in a few papers (Ditlevsen and De Gaetano, 2005 [11]; Donnet and Samson, 2008 [12]; Delattre et al. (2013) [8]; Alkreemawi et al. ([2], [3]); Alsukaini et al. ([4], [5]). In this paper, we assume that the random variables
which will be estimated, but the estimation is not straightforward. Generally, the exact likelihood is not explicit. Maximum likelihood estimation in SDE with random effects has been studied in a few papers (Ditlevsen and De Gaetano, 2005 [11]; Donnet and Samson, 2008 [12]; Delattre et al. (2013) [8]; Alkreemawi et al. ([2], [3]); Alsukaini et al. ([4], [5]). In this paper, we assume that the random variables 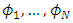 have a common distribution with density
have a common distribution with density 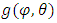 for all
for all 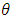 , which is given by a mixture of Gaussian distributions; this mixture distribution models the classes. We aim to estimate unknown parameters and study the proportions.
, which is given by a mixture of Gaussian distributions; this mixture distribution models the classes. We aim to estimate unknown parameters and study the proportions. 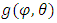 is a density with respect to a dominant measure on
is a density with respect to a dominant measure on  , where
, where 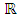 is the real line, and
is the real line, and  is the dimension.
is the dimension. with
with 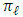 as the proportions of the mixture
as the proportions of the mixture  ,
, 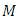 as the number of components in the mixture, and
as the number of components in the mixture, and 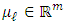 and
and 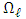 a
a 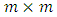 as an invertible covariance matrix. Let
as an invertible covariance matrix. Let 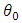 denote the true value of the parameter. M is the number of components and is known.
denote the true value of the parameter. M is the number of components and is known. 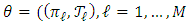 is set for the unknown parameters to be estimated. Our aim is to find estimators of the parameters
is set for the unknown parameters to be estimated. Our aim is to find estimators of the parameters  of the density of the random effects from the observations
of the density of the random effects from the observations 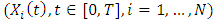 . We focus on an additional case of linear random effects
. We focus on an additional case of linear random effects  in the drift term
in the drift term  . In addition, we prove and explain that the observations concerning exact likelihood are explicit. With M as the number of known components, we discuss the convergence of the EM algorithm, and the consistency of the exact maximum likelihood estimator is proven. The rest of this paper is organized as follows: Section 2 contains the notation and assumptions, and we present the formula of the exact likelihood. In Section 3, we describe the EM algorithm and discuss its convergence. In Section 4, the consistency of the exact maximum likelihood estimator is proved when the number of components is known.
. In addition, we prove and explain that the observations concerning exact likelihood are explicit. With M as the number of known components, we discuss the convergence of the EM algorithm, and the consistency of the exact maximum likelihood estimator is proven. The rest of this paper is organized as follows: Section 2 contains the notation and assumptions, and we present the formula of the exact likelihood. In Section 3, we describe the EM algorithm and discuss its convergence. In Section 4, the consistency of the exact maximum likelihood estimator is proved when the number of components is known.
2. Notations and Assumptions
Consider the stochastic processes 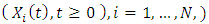 , which are defined by (1). The processes
, which are defined by (1). The processes 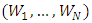 and the random variables
and the random variables 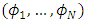 are defined on the probability space
are defined on the probability space  . We use the assumptions (H1, H2, and H3) in Delattre et al. [9]. Consider the filtration
. We use the assumptions (H1, H2, and H3) in Delattre et al. [9]. Consider the filtration  defined by
defined by 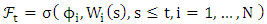 .H1. The functions
.H1. The functions 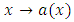 and
and 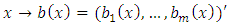 are Lipschitz continuous on
are Lipschitz continuous on  and
and 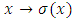 is Hölder continuous with exponent
is Hölder continuous with exponent 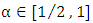 on
on 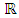 .By (H1), for
.By (H1), for 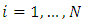 , for all
, for all 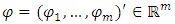 , the stochastic differential equation
, the stochastic differential equation 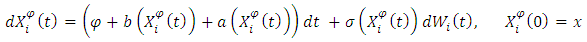 | (2) |
admits a unique solution process 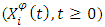 adapted to the filtration
adapted to the filtration 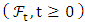 , Moreover, the stochastic differential equation (1) admits a unique strong solution adapted to
, Moreover, the stochastic differential equation (1) admits a unique strong solution adapted to 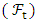 such that the joint process
such that the joint process 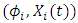 is strong Markov and the conditional distribution of
is strong Markov and the conditional distribution of  given
given 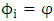 is identical to the distribution of (2). (1) shows that the Markov property of
is identical to the distribution of (2). (1) shows that the Markov property of 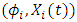 is straightforward as the two-dimensional SDE
is straightforward as the two-dimensional SDE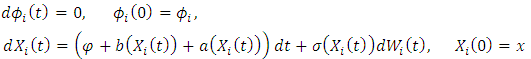 The processes
The processes 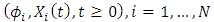 are
are 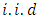 (see Delattre et al. [8]; Genon-Catalot and Larédo [13], Alkreemawi et al. [2], [3]; Alsukaini et al. [4], [5]). To derive the likelihood function of our observations, under (H1), we introduce the distribution
(see Delattre et al. [8]; Genon-Catalot and Larédo [13], Alkreemawi et al. [2], [3]; Alsukaini et al. [4], [5]). To derive the likelihood function of our observations, under (H1), we introduce the distribution 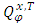 on
on 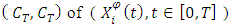 given by (2), where
given by (2), where 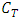 denotes the space of real continuous functions
denotes the space of real continuous functions 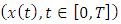 defined on
defined on 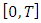 endowed with the
endowed with the 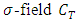 associated with the topology of uniform convergence on
associated with the topology of uniform convergence on 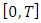 . On
. On 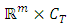 , let
, let 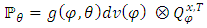 denote the joint distribution of
denote the joint distribution of 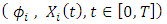 , and let
, and let  denote the marginal distribution of
denote the marginal distribution of  on
on  . Also, we denote
. Also, we denote  ,
,  (resp.
(resp. 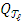 ) the distribution
) the distribution  of
of 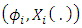 where
where 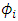 has a distribution
has a distribution 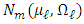 (resp. of
(resp. of 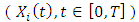 ), with these notations
), with these notations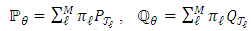 | (3) |
H2. For all  ,
, We denote by
We denote by 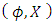 , with
, with 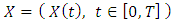 , which is the canonical process of
, which is the canonical process of  . Under (H1)–(H2), based on Theorem 7.19 p. 294 in [14], the distributions
. Under (H1)–(H2), based on Theorem 7.19 p. 294 in [14], the distributions 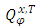 and
and 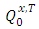 are equivalent. Through an analog approach of [9], the following results are used:
are equivalent. Through an analog approach of [9], the following results are used: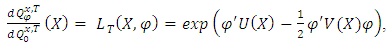 where
where  is the vector, and
is the vector, and 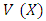 is the
is the 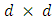 matrix
matrix 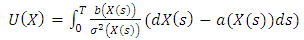 | (4) |
and  is the
is the 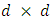 matrix
matrix 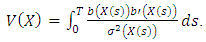 | (5) |
Thus, the density of 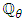 (the distribution of
(the distribution of 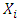 on
on 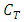 ) with respect to
) with respect to 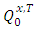 is obtained as follows:
is obtained as follows: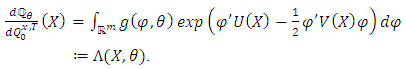 | (6) |
The exact likelihood of  is
is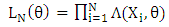 | (7) |
Thus, for our situation (addition situation) of drift where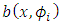 is linear in
is linear in 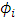 ,
, 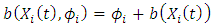 , we have
, we have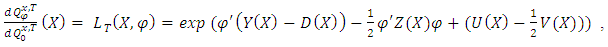 and,
and, 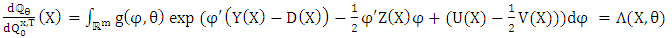 | (8) |
where 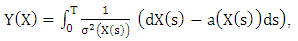 | (9) |
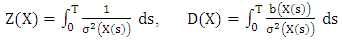 | (10) |
We have to consider distributions for 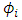 such that the integral (8) can obtain a tractable formula for the exact likelihood. This is the case when
such that the integral (8) can obtain a tractable formula for the exact likelihood. This is the case when 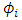 has a Gaussian distribution and the drift term
has a Gaussian distribution and the drift term 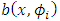 is linear in
is linear in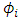 ,
, 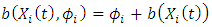 (addition situation), as shown in Alkreemawi et al. [2]. This is also the case for the larger class of Gaussian mixtures. The required assumption is defined as follows:H3. The matrix
(addition situation), as shown in Alkreemawi et al. [2]. This is also the case for the larger class of Gaussian mixtures. The required assumption is defined as follows:H3. The matrix 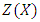 is positive definite
is positive definite 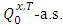 and
and 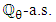 for all
for all 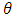 .(H3) is not true when the functions
.(H3) is not true when the functions  and
and 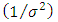 are not linearly independent. Thus, (H3) can ensure a well-defined dimension of the vector
are not linearly independent. Thus, (H3) can ensure a well-defined dimension of the vector 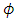 .Proposition 2.1. Assume that
.Proposition 2.1. Assume that  is a Gaussian mixture distribution, and set
is a Gaussian mixture distribution, and set 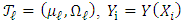 ,
,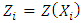 ,
,  ,
, 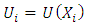 ,
, 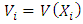 . Under (H3), the matrices
. Under (H3), the matrices  are invertible
are invertible 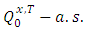 and
and 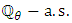 for all
for all  . By setting
. By setting 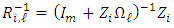 , we obtain,
, we obtain, 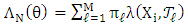 | (11) |
where 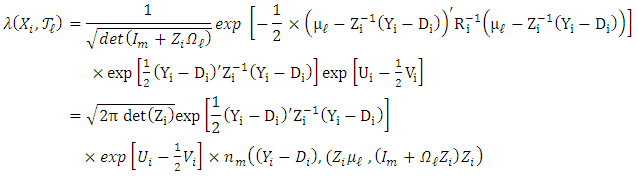 | (12) |
Here, 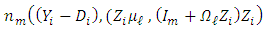 denotes the Gaussian density with mean
denotes the Gaussian density with mean 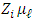 and covariance matrix
and covariance matrix  .Alkreemawi et al. [2] considered the formula for
.Alkreemawi et al. [2] considered the formula for 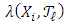 (Proposition 3.1.1 and Lemma 4.2). The exact likelihood (7) is explicit. Hence, we can study the asymptotic properties of the exact MLE, which can be computed by using the EM algorithm instead of maximizing the likelihood.
(Proposition 3.1.1 and Lemma 4.2). The exact likelihood (7) is explicit. Hence, we can study the asymptotic properties of the exact MLE, which can be computed by using the EM algorithm instead of maximizing the likelihood.
3. Estimation Algorithm
In the situation of mixtures distributions with number of components M, M is known, rather than of solving the likelihood equation, we use the EM algorithm to find a stationary point of the log-likelihood. A Gaussian mixture model (GMM) is helpful for modeling 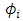 by using a mixture of distributions, which means that the population of individuals is grouped in M clusters. Formally, for the individual i, we (may) introduce a random variable
by using a mixture of distributions, which means that the population of individuals is grouped in M clusters. Formally, for the individual i, we (may) introduce a random variable 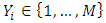 , with
, with  and
and 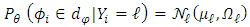 . We assume that
. We assume that 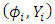 are
are 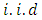 and
and 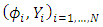 independent of
independent of  . The concept of the EM algorithm was presented in Dempster et al. [10] which considered the data
. The concept of the EM algorithm was presented in Dempster et al. [10] which considered the data 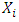 as incomplete and introduced the unobserved variables
as incomplete and introduced the unobserved variables  . Simply, in the algorithm, we can consider random variables
. Simply, in the algorithm, we can consider random variables  where
where 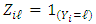 , for
, for 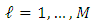 ; such values indicate that the density component drives the equation of subject i. For the complete data
; such values indicate that the density component drives the equation of subject i. For the complete data 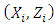 , the logarithm likelihood function is explicitly given by
, the logarithm likelihood function is explicitly given by 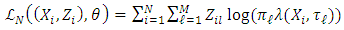 | (13) |
The EM algorithm is an iterative method in which the iteration alternates between performing an expectation (E) step, which is the computation of where
where 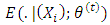 is the conditional expectation given
is the conditional expectation given  computed with the distribution of the complete data under the value
computed with the distribution of the complete data under the value 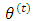 of the parameter, and the maximization (M) step computes parameters that maximize the expected log-likelihood found on the (E) step
of the parameter, and the maximization (M) step computes parameters that maximize the expected log-likelihood found on the (E) step 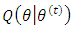 . In the (E) step, we compute
. In the (E) step, we compute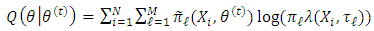 where
where  is the posterior probability
is the posterior probability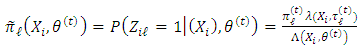 | (14) |
In the EM algorithm, at iteration n, we want to maximize 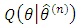 with respect to
with respect to 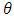 , where
, where 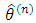 is the current value of parameter
is the current value of parameter  . We can maximize the terms that contain
. We can maximize the terms that contain 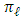 and
and 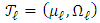 separately. We introduce one Lagrange multiplier
separately. We introduce one Lagrange multiplier 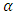 to maximize with respect to
to maximize with respect to  with the constraint
with the constraint  and solve the following equation:
and solve the following equation: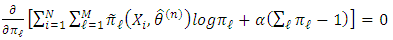 And the classical solution:
And the classical solution: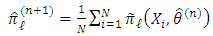 Then, we maximize
Then, we maximize 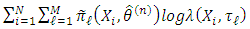 , where the derivatives can be computed with respect to the components of
, where the derivatives can be computed with respect to the components of 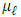 and
and 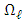 by using some results from matrix algebra. When taking the log of
by using some results from matrix algebra. When taking the log of 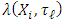 , substituting it into
, substituting it into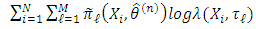 , and taking the derivative w.r.t.
, and taking the derivative w.r.t. 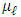 , we have
, we have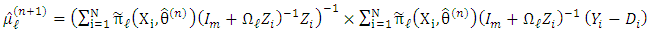 | (15) |
When the 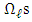 are known and when the
are known and when the  are unknown, the maximum likelihood estimators of the parameters are given by the system.Proposition 3.1 The sequence
are unknown, the maximum likelihood estimators of the parameters are given by the system.Proposition 3.1 The sequence  generated by the EM algorithm converges to a stationary point of the likelihood.Proof. We prove the convergence for
generated by the EM algorithm converges to a stationary point of the likelihood.Proof. We prove the convergence for  to avoid cumbersome details. We employ the results obtained by McLachlan and Krishnan [15]. As the following conditions are given:
to avoid cumbersome details. We employ the results obtained by McLachlan and Krishnan [15]. As the following conditions are given:  Conditions 3, 4, 5, and 6 are verified by the regularity of the likelihood (see Proposition 4.2). In a standard Gaussian mixture, condition 2 is usually unverified (see McLachlan and Krishnan [15]. However, here, one has the following result (see (12)):
Conditions 3, 4, 5, and 6 are verified by the regularity of the likelihood (see Proposition 4.2). In a standard Gaussian mixture, condition 2 is usually unverified (see McLachlan and Krishnan [15]. However, here, one has the following result (see (12)): Where
Where  . Therefore, the formula of
. Therefore, the formula of 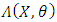 is a mixture of Gaussian distributions that consist of variances all bounded from below. This finding reveals condition 2.
is a mixture of Gaussian distributions that consist of variances all bounded from below. This finding reveals condition 2.
4. Asymptotic Properties of MLE
This section aims to investigate theoretically the consistency and asymptotic normality of the exact maximum likelihood estimator of 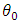 when we assume that the number of components M is known. For simplicity’s sake, we consider only the case
when we assume that the number of components M is known. For simplicity’s sake, we consider only the case  . The parameter set
. The parameter set 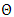 is given by
is given by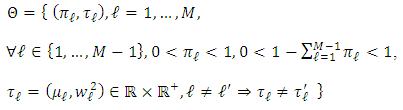 Now, we set
Now, we set 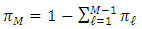 , but only
, but only 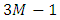 parameters need to be estimated. When necessary in notations, we set
parameters need to be estimated. When necessary in notations, we set 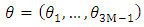 . The MLE is defined as any solution of
. The MLE is defined as any solution of where
where  is defined by (7)–(11). To prove the identifiability property, the following assumption is required as in Alkreemawi et al. [2]:(H4) Either the function
is defined by (7)–(11). To prove the identifiability property, the following assumption is required as in Alkreemawi et al. [2]:(H4) Either the function  is constant or not constant, and under
is constant or not constant, and under 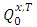 , the random variable
, the random variable 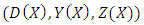 admits a density
admits a density 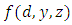 with respect to the Lebesgue measure on
with respect to the Lebesgue measure on 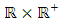 , which is jointly continuous and positive on an open ball of
, which is jointly continuous and positive on an open ball of 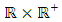 .When
.When 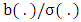 is constant, this case is simple. For instance, let
is constant, this case is simple. For instance, let 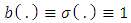 . Then,
. Then, 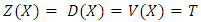 is deterministic, and under
is deterministic, and under 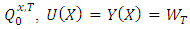 . Under
. Under is a mixture of Gaussian distributions with means
is a mixture of Gaussian distributions with means 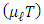 , variances
, variances 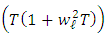 , and proportions
, and proportions 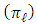 .The case where
.The case where 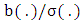 is not constant. Under smoothness assumptions on functions
is not constant. Under smoothness assumptions on functions  , assumption (H4) will be accomplished by using Malliavin calculus tools (see Alkreemawi et al. [2]). As mixture distributions are utilized, the identifiability of the entire parameter
, assumption (H4) will be accomplished by using Malliavin calculus tools (see Alkreemawi et al. [2]). As mixture distributions are utilized, the identifiability of the entire parameter  can only be obtained in the following concept:
can only be obtained in the following concept: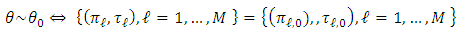 | (16) |
Now, we can prove the following:Proposition 4.1. Under (H1)-(H2)-(H4), 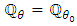 implies that
implies that  .Proof. First, when
.Proof. First, when 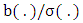 is not constant, we consider two parameters
is not constant, we consider two parameters 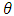 and
and 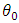 , and aim to prove that
, and aim to prove that  implies
implies  . As
. As 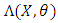 and
and 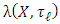 depend on
depend on 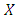 only through the statistics
only through the statistics 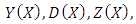
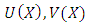 with a slight abuse of notation, we set
with a slight abuse of notation, we set 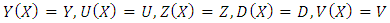 and
and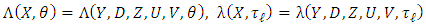 | (17) |
Under (H4), 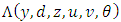 is the density of the distribution of
is the density of the distribution of  under
under 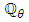 with respect to the density of
with respect to the density of 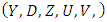 under
under  and
and 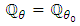 implies
implies  a.e., hence, everywhere on
a.e., hence, everywhere on  by the continuity assumption. We deduce that the following equality holds for all
by the continuity assumption. We deduce that the following equality holds for all 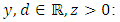
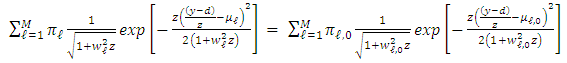 Let us set
Let us set and
and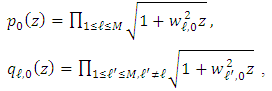 We note that
We note that  . Thus, such quantities do not depend on
. Thus, such quantities do not depend on 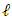 . After reducing to the same denominator, we obtain
. After reducing to the same denominator, we obtain The right-hand side is a function of
The right-hand side is a function of 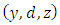 , whereas the left-hand side is a function of z only. This approach is possible only if
, whereas the left-hand side is a function of z only. This approach is possible only if 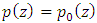 for all
for all  . Therefore,
. Therefore, 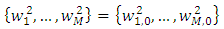 | (18) |
and the equality of the variances can be obtained by reordering the terms if required. Then, we have for 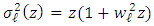 and a fixed z,
and a fixed z,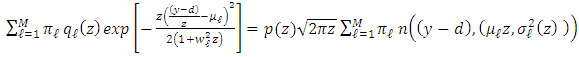 | (19) |
Here,  indicates the Gaussian density with mean m and variance
indicates the Gaussian density with mean m and variance  . Analogously, by using the equality (18),
. Analogously, by using the equality (18),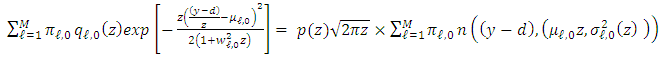 For all fixed
For all fixed 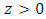 , we therefore have for all
, we therefore have for all 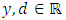 ,
, 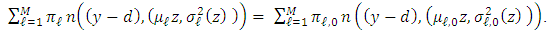 Herein, the equality of two mixtures of Gaussian distributions with proportions
Herein, the equality of two mixtures of Gaussian distributions with proportions 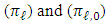 , expectations
, expectations  and
and 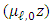 , and the same set of known variances
, and the same set of known variances 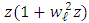 are given. From the identifiability of Gaussian mixtures, we have the equality
are given. From the identifiability of Gaussian mixtures, we have the equality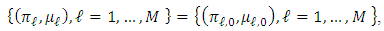 and thus,
and thus, 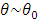 .Second, when
.Second, when  is constant, for instance, let
is constant, for instance, let 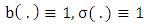 . As noted above, under
. As noted above, under 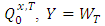 and
and 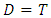 . Therefore,
. Therefore, 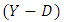 is a Gaussian distribution. Under
is a Gaussian distribution. Under  ,
,  has density
has density 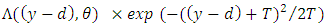 w. r. t. the Lebesgue measure on
w. r. t. the Lebesgue measure on 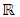 . Specifically, the mixture of Gaussian densities can also be deduced based on the identifiability property of Gaussian mixtures.Proposition 4.2. Let
. Specifically, the mixture of Gaussian densities can also be deduced based on the identifiability property of Gaussian mixtures.Proposition 4.2. Let  denote the expectation under
denote the expectation under 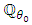 . The function
. The function  is
is 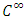 on
on  and
and 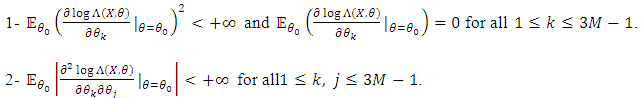
 for all
for all 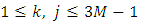 .The Fisher information matrix can be defined as
.The Fisher information matrix can be defined as 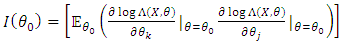 for all
for all 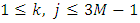 . Proof. We use results proved in Alkreemawi el al. [2] (Section 3.1, Lemma 3.1.1, Proposition 3.1.2) to prove this proposition. For all
. Proof. We use results proved in Alkreemawi el al. [2] (Section 3.1, Lemma 3.1.1, Proposition 3.1.2) to prove this proposition. For all 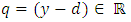 and all
and all  ,
,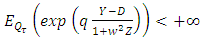
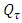 is the distribution of
is the distribution of 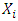 when
when 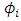 has a Gaussian distribution with parameters
has a Gaussian distribution with parameters 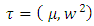 . This idea implies that
. This idea implies that 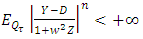 for all
for all  . Let
. Let The random variable that has moments of any order under
The random variable that has moments of any order under  is bounded, and the following relations hold:
is bounded, and the following relations hold: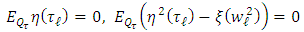 | (20) |
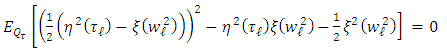 | (21) |
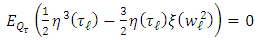 | (22) |
All derivatives of  are well defined. For
are well defined. For  , we have
, we have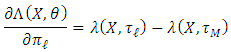 As for all
As for all 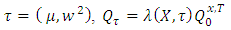 , the random variable above is
, the random variable above is 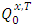 -integrable and
-integrable and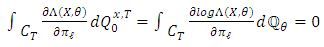 Moreover, as
Moreover, as 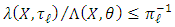 , we have
, we have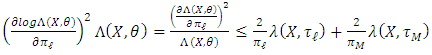 Therefore,
Therefore, 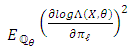
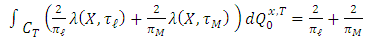 Higher order derivatives of
Higher order derivatives of 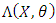 with respect to the
with respect to the 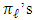 are nul:
are nul: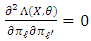 Now we find the derivatives with respect to the parameters
Now we find the derivatives with respect to the parameters 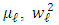 . We have:
. We have: 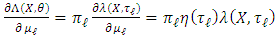 We know that:
We know that: 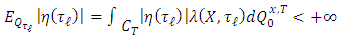
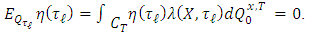 Consequently,
Consequently,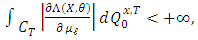
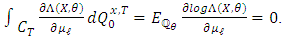 Now,
Now,  Thus,
Thus,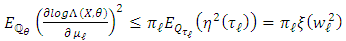 Next, we have
Next, we have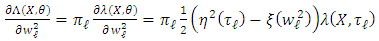 Again, we know that this random variable is
Again, we know that this random variable is  -integrable with nul integral, thereby obtaining
-integrable with nul integral, thereby obtaining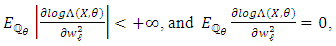 Moreover,
Moreover,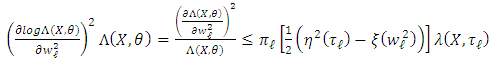 This finding implies that
This finding implies that Now we look at second-order derivatives. The successive derivatives with respect to
Now we look at second-order derivatives. The successive derivatives with respect to 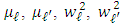 with
with 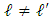 are nul. We obtain
are nul. We obtain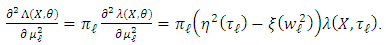 This random variable is integrable with respect to
This random variable is integrable with respect to  with the nul integral. Thus,
with the nul integral. Thus,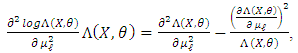 We find that this random variable is integrable with respect to
We find that this random variable is integrable with respect to  , and computing the integral obtains
, and computing the integral obtains 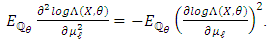 Next,
Next,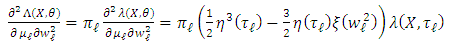
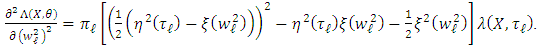 Thus, we conclude the proof analogously using (21) and (22).Proposition 4.3. Assume that
Thus, we conclude the proof analogously using (21) and (22).Proposition 4.3. Assume that 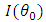 is invertible and (H1)–(H2). Then, an estimator
is invertible and (H1)–(H2). Then, an estimator 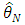 solves the likelihood estimating equation
solves the likelihood estimating equation  with a probability tending to 1 and
with a probability tending to 1 and 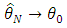 in probability.Proof. For weak consistency following the standard steps, the uniformity condition needs to be proven. We prove that An open convex subset
in probability.Proof. For weak consistency following the standard steps, the uniformity condition needs to be proven. We prove that An open convex subset 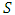 of
of  exists, which contains
exists, which contains  and functions
and functions 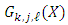 such that, on S,
such that, on S,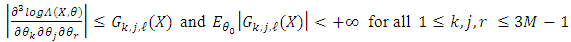 .
.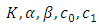 are set as positive numbers such that
are set as positive numbers such that 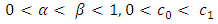 , and
, and 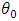 is assumed to belong to
is assumed to belong to  where
where  . We have to study
. We have to study 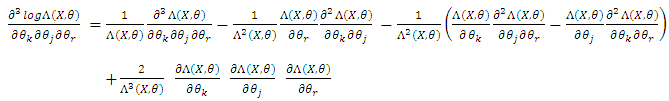 Therefore, we have, for
Therefore, we have, for 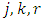 distinct indexes
distinct indexes As
As  ,
, We use
We use 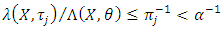 again to bound the other third-order derivatives. Then, in the derivatives, random variables appear
again to bound the other third-order derivatives. Then, in the derivatives, random variables appear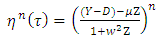 for different values of n. We now bound
for different values of n. We now bound 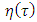 by an r. v. independent of
by an r. v. independent of  and have moments of any order under
and have moments of any order under 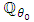 . We have
. We have Thus,
Thus,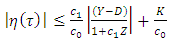 Now, in the same method
Now, in the same method 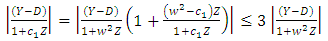 For all
For all 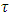 , this finding implies that
, this finding implies that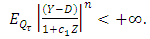 Consequently,
Consequently, The proof of Proposition 4.3 is complete.
The proof of Proposition 4.3 is complete.
5. Conclusions
In stochastic differential equations based random effects model framework. We considered the addition case in the drift where 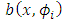 is linear in
is linear in  , where
, where  has a mixture of Gaussian. We obtain an expression of the exact likelihood. When the number of components is known, we prove the consistency of the maximum likelihood estimators (MLEs). Properties of the EM algorithm are described when the algorithm is used to compute MLE.
has a mixture of Gaussian. We obtain an expression of the exact likelihood. When the number of components is known, we prove the consistency of the maximum likelihood estimators (MLEs). Properties of the EM algorithm are described when the algorithm is used to compute MLE.
ACKNOWLEDGEMENTS
The Author is grateful to Dr. Wang Xiang jun of School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan, Hubei, 430074 P.R. China. Also, to Mr. Alsukaini M. S. of the department of Mathematics, College of Science, Basra University, Basra, Iraq for their constructive comments.
References
| [1] | Arribas-Gil, A., De la Cruz, R., Lebarbier, E. and Meza, C. (2015). Classification of longitudinal data through a semiparametric mixed-effects model based on lasso-type estimators. Biometrics 71, 333–343. |
| [2] | Alkreemawi W. K., Alsukaini M. S. and Wang X. J. “On Parameters Estimation in Stochastic Differential Equations with Additive Random Effects,” Journal of Advances in Mathematics, Vol. 11, no.3, 5018 – 5028, 2015. |
| [3] | Alkreemawi W. K., Alsukaini M. S. and Wang X. J. “Asymptotic Properties of MLE in Stochastic Differential Equations with Random Effects in the Drift Coefficient,” International Journal of Engineering, Science and Mathematics (IJESM), Vol. 5, Issue. 1, 1 – 14, 2016. |
| [4] | Alsukaini M. S., Alkreemawi W. K. and Wang X. J., “Asymptotic Properties of MLE in Stochastic Differential Equations with Random Effects in the Diffusion Coefficient,” International Journal of Contemporary Mathematical Sciences, Vol. 10, no. 6, 275 – 286, 2015. |
| [5] | Alsukaini M. S., Alkreemawi W. K. and Wang X. J., “ Maximum likelihood Estimation for Stochastic Differential Equations with two Random Effects in the Diffusion Coefficient,” Journal of Advances in Mathematics, Vol. 11, no.10, 5697 – 5704, 2016. |
| [6] | Celeux, G., Martin, O. and Lavergne, C. (2005). Mixture of linear mixed models application to repeated data clustering. Statistical Modelling 5, 243–267. |
| [7] | Comte, F., Genon-Catalot, V. and Samson, A. (2013). Nonparametric estimation for stochastic differential equations with random effects. Stoch. Proc. Appl. 123, 2522–2551. |
| [8] | Delattre M., Genon Catalot V. and Samson A., “Maximum Likelihood Estimation for Stochastic Differential Equations with Random Effects,” Scandinavian Journal of Statistics, 40, 322-343, 2013. |
| [9] | Delattre M., Genon Catalot V. and Samson A., “Mixtures of stochastic differential equations with random effects: application to data clustering,” Journal of statistical planning and inference, Publication MAP5-2015-36. |
| [10] | Dempster, A., Laird, N. and Rubin, D. (1977). Maximum likelihood from incomplete data via the EM algorithm. Jr. R. Stat. Soc. B 39, 1–38. |
| [11] | Ditlevsen, S. and De Gaetano, A. (2005). Stochastic vs. deterministic uptake of dodecanedioic acid by isolated rat livers. Bull. Math. Biol. 67, 547–561. |
| [12] | Donnet, S. and Samson, A. (2008). Parametric infer ence for mixed models defined by stochastic differential equations. ESAIM P&S 12, 196–218. |
| [13] | Genon-Catalot, V. and Larédo, C. (2015). Estimation for stochastic differential equations with mixed effects. Hal-00807258 V2. |
| [14] | Lipster, R. and Shiryaev, A. (2001). Statistics of random processes I: general theory. Springer. |
| [15] | McLachlan, G. and Krishnan, T. (2008). The EM Algorithm and Extensions. |


 The drift term depends on the random variable
The drift term depends on the random variable  . The distribution of the random effect
. The distribution of the random effect 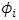 depends on unknown parameters, which are to be estimated from continuous observation of the processes
depends on unknown parameters, which are to be estimated from continuous observation of the processes 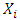 . When the drift term is defined linearly on the random effect
. When the drift term is defined linearly on the random effect 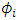 (additive random effect) and
(additive random effect) and 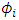 has a Gaussian mixture distribution, we obtain an expression of the exact likelihood. When the number of components is known, we prove the consistency of the maximum likelihood estimators
has a Gaussian mixture distribution, we obtain an expression of the exact likelihood. When the number of components is known, we prove the consistency of the maximum likelihood estimators 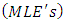 . The convergence of the EM algorithm described when the algorithm is used to compute
. The convergence of the EM algorithm described when the algorithm is used to compute 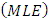 .
.
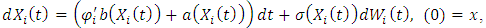
 are
are  independent Wiener processes,
independent Wiener processes,  are
are 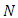 independently and identically distributed
independently and identically distributed  random variables. The processes
random variables. The processes 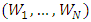 are also independent on random variables
are also independent on random variables 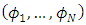 , and
, and 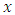 is a known real value. The drift function
is a known real value. The drift function 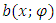 is a known function defined on
is a known function defined on  and the functions
and the functions 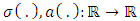 . Each process
. Each process  represents an individual, and the random variable
represents an individual, and the random variable  represents the random effect of individual i.Delattre et al. [2] considered the special case (multiple case) where
represents the random effect of individual i.Delattre et al. [2] considered the special case (multiple case) where 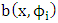 is linear in
is linear in 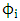 ; in other words,
; in other words,  , where
, where 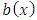 is a known real function, and
is a known real function, and 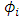 has a Gaussian mixture distribution.Here, we consider functional data modeled by a SDE with drift term
has a Gaussian mixture distribution.Here, we consider functional data modeled by a SDE with drift term 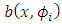 depending on random effects where
depending on random effects where  is linear in random effects
is linear in random effects  (addition case),
(addition case),  and diffusion term without random effects. We consider continuous observations
and diffusion term without random effects. We consider continuous observations 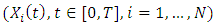 with a given
with a given 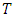 . Here,
. Here,  are unknown parameters in the distribution of
are unknown parameters in the distribution of  from the
from the 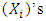 which will be estimated, but the estimation is not straightforward. Generally, the exact likelihood is not explicit. Maximum likelihood estimation in SDE with random effects has been studied in a few papers (Ditlevsen and De Gaetano, 2005 [11]; Donnet and Samson, 2008 [12]; Delattre et al. (2013) [8]; Alkreemawi et al. ([2], [3]); Alsukaini et al. ([4], [5]). In this paper, we assume that the random variables
which will be estimated, but the estimation is not straightforward. Generally, the exact likelihood is not explicit. Maximum likelihood estimation in SDE with random effects has been studied in a few papers (Ditlevsen and De Gaetano, 2005 [11]; Donnet and Samson, 2008 [12]; Delattre et al. (2013) [8]; Alkreemawi et al. ([2], [3]); Alsukaini et al. ([4], [5]). In this paper, we assume that the random variables 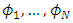 have a common distribution with density
have a common distribution with density 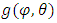 for all
for all 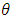 , which is given by a mixture of Gaussian distributions; this mixture distribution models the classes. We aim to estimate unknown parameters and study the proportions.
, which is given by a mixture of Gaussian distributions; this mixture distribution models the classes. We aim to estimate unknown parameters and study the proportions. 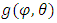 is a density with respect to a dominant measure on
is a density with respect to a dominant measure on  , where
, where 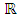 is the real line, and
is the real line, and  is the dimension.
is the dimension. with
with 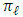 as the proportions of the mixture
as the proportions of the mixture  ,
, 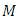 as the number of components in the mixture, and
as the number of components in the mixture, and 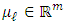 and
and 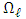 a
a 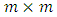 as an invertible covariance matrix. Let
as an invertible covariance matrix. Let 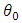 denote the true value of the parameter. M is the number of components and is known.
denote the true value of the parameter. M is the number of components and is known. 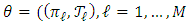 is set for the unknown parameters to be estimated. Our aim is to find estimators of the parameters
is set for the unknown parameters to be estimated. Our aim is to find estimators of the parameters  of the density of the random effects from the observations
of the density of the random effects from the observations 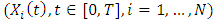 . We focus on an additional case of linear random effects
. We focus on an additional case of linear random effects  in the drift term
in the drift term  . In addition, we prove and explain that the observations concerning exact likelihood are explicit. With M as the number of known components, we discuss the convergence of the EM algorithm, and the consistency of the exact maximum likelihood estimator is proven. The rest of this paper is organized as follows: Section 2 contains the notation and assumptions, and we present the formula of the exact likelihood. In Section 3, we describe the EM algorithm and discuss its convergence. In Section 4, the consistency of the exact maximum likelihood estimator is proved when the number of components is known.
. In addition, we prove and explain that the observations concerning exact likelihood are explicit. With M as the number of known components, we discuss the convergence of the EM algorithm, and the consistency of the exact maximum likelihood estimator is proven. The rest of this paper is organized as follows: Section 2 contains the notation and assumptions, and we present the formula of the exact likelihood. In Section 3, we describe the EM algorithm and discuss its convergence. In Section 4, the consistency of the exact maximum likelihood estimator is proved when the number of components is known.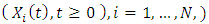 , which are defined by (1). The processes
, which are defined by (1). The processes 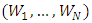 and the random variables
and the random variables 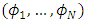 are defined on the probability space
are defined on the probability space  . We use the assumptions (H1, H2, and H3) in Delattre et al. [9]. Consider the filtration
. We use the assumptions (H1, H2, and H3) in Delattre et al. [9]. Consider the filtration  defined by
defined by 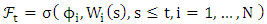 .H1. The functions
.H1. The functions 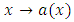 and
and 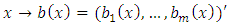 are Lipschitz continuous on
are Lipschitz continuous on  and
and 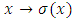 is Hölder continuous with exponent
is Hölder continuous with exponent 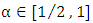 on
on 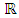 .By (H1), for
.By (H1), for 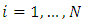 , for all
, for all 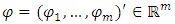 , the stochastic differential equation
, the stochastic differential equation 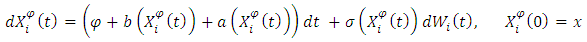
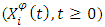 adapted to the filtration
adapted to the filtration 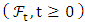 , Moreover, the stochastic differential equation (1) admits a unique strong solution adapted to
, Moreover, the stochastic differential equation (1) admits a unique strong solution adapted to 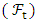 such that the joint process
such that the joint process 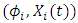 is strong Markov and the conditional distribution of
is strong Markov and the conditional distribution of  given
given 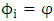 is identical to the distribution of (2). (1) shows that the Markov property of
is identical to the distribution of (2). (1) shows that the Markov property of 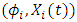 is straightforward as the two-dimensional SDE
is straightforward as the two-dimensional SDE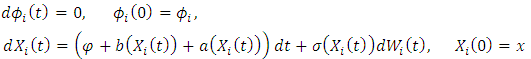 The processes
The processes 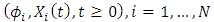 are
are 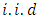 (see Delattre et al. [8]; Genon-Catalot and Larédo [13], Alkreemawi et al. [2], [3]; Alsukaini et al. [4], [5]). To derive the likelihood function of our observations, under (H1), we introduce the distribution
(see Delattre et al. [8]; Genon-Catalot and Larédo [13], Alkreemawi et al. [2], [3]; Alsukaini et al. [4], [5]). To derive the likelihood function of our observations, under (H1), we introduce the distribution 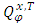 on
on 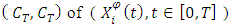 given by (2), where
given by (2), where 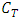 denotes the space of real continuous functions
denotes the space of real continuous functions 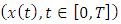 defined on
defined on 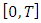 endowed with the
endowed with the 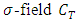 associated with the topology of uniform convergence on
associated with the topology of uniform convergence on 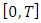 . On
. On 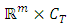 , let
, let 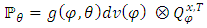 denote the joint distribution of
denote the joint distribution of 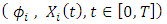 , and let
, and let  denote the marginal distribution of
denote the marginal distribution of  on
on  . Also, we denote
. Also, we denote  ,
,  (resp.
(resp. 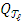 ) the distribution
) the distribution  of
of 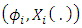 where
where 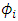 has a distribution
has a distribution 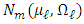 (resp. of
(resp. of 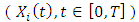 ), with these notations
), with these notations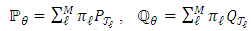
 ,
, We denote by
We denote by 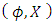 , with
, with 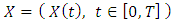 , which is the canonical process of
, which is the canonical process of  . Under (H1)–(H2), based on Theorem 7.19 p. 294 in [14], the distributions
. Under (H1)–(H2), based on Theorem 7.19 p. 294 in [14], the distributions 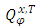 and
and 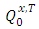 are equivalent. Through an analog approach of [9], the following results are used:
are equivalent. Through an analog approach of [9], the following results are used: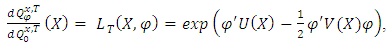 where
where  is the vector, and
is the vector, and 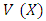 is the
is the 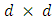 matrix
matrix 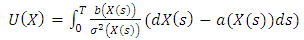
 is the
is the 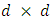 matrix
matrix 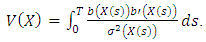
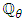 (the distribution of
(the distribution of 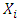 on
on 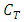 ) with respect to
) with respect to 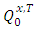 is obtained as follows:
is obtained as follows: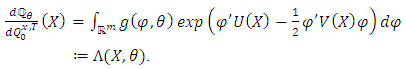
 is
is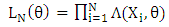
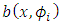 is linear in
is linear in 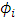 ,
, 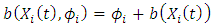 , we have
, we have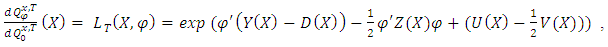 and,
and, 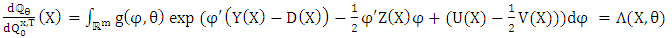
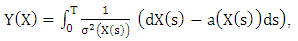
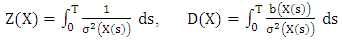
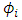 such that the integral (8) can obtain a tractable formula for the exact likelihood. This is the case when
such that the integral (8) can obtain a tractable formula for the exact likelihood. This is the case when 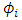 has a Gaussian distribution and the drift term
has a Gaussian distribution and the drift term 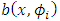 is linear in
is linear in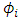 ,
, 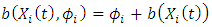 (addition situation), as shown in Alkreemawi et al. [2]. This is also the case for the larger class of Gaussian mixtures. The required assumption is defined as follows:H3. The matrix
(addition situation), as shown in Alkreemawi et al. [2]. This is also the case for the larger class of Gaussian mixtures. The required assumption is defined as follows:H3. The matrix 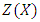 is positive definite
is positive definite 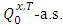 and
and 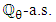 for all
for all 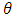 .(H3) is not true when the functions
.(H3) is not true when the functions  and
and 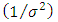 are not linearly independent. Thus, (H3) can ensure a well-defined dimension of the vector
are not linearly independent. Thus, (H3) can ensure a well-defined dimension of the vector 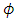 .Proposition 2.1. Assume that
.Proposition 2.1. Assume that  is a Gaussian mixture distribution, and set
is a Gaussian mixture distribution, and set 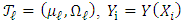 ,
,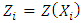 ,
,  ,
, 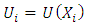 ,
, 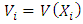 . Under (H3), the matrices
. Under (H3), the matrices  are invertible
are invertible 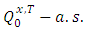 and
and 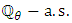 for all
for all  . By setting
. By setting 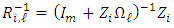 , we obtain,
, we obtain, 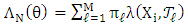
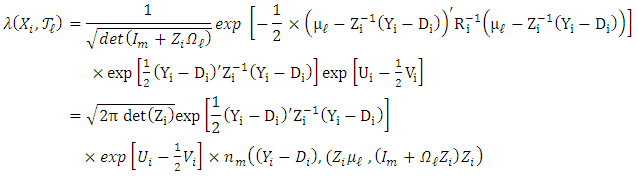
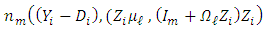 denotes the Gaussian density with mean
denotes the Gaussian density with mean 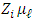 and covariance matrix
and covariance matrix  .Alkreemawi et al. [2] considered the formula for
.Alkreemawi et al. [2] considered the formula for 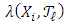 (Proposition 3.1.1 and Lemma 4.2). The exact likelihood (7) is explicit. Hence, we can study the asymptotic properties of the exact MLE, which can be computed by using the EM algorithm instead of maximizing the likelihood.
(Proposition 3.1.1 and Lemma 4.2). The exact likelihood (7) is explicit. Hence, we can study the asymptotic properties of the exact MLE, which can be computed by using the EM algorithm instead of maximizing the likelihood.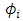 by using a mixture of distributions, which means that the population of individuals is grouped in M clusters. Formally, for the individual i, we (may) introduce a random variable
by using a mixture of distributions, which means that the population of individuals is grouped in M clusters. Formally, for the individual i, we (may) introduce a random variable 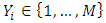 , with
, with  and
and 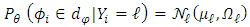 . We assume that
. We assume that 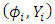 are
are 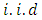 and
and 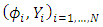 independent of
independent of  . The concept of the EM algorithm was presented in Dempster et al. [10] which considered the data
. The concept of the EM algorithm was presented in Dempster et al. [10] which considered the data 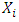 as incomplete and introduced the unobserved variables
as incomplete and introduced the unobserved variables  . Simply, in the algorithm, we can consider random variables
. Simply, in the algorithm, we can consider random variables  where
where 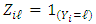 , for
, for 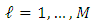 ; such values indicate that the density component drives the equation of subject i. For the complete data
; such values indicate that the density component drives the equation of subject i. For the complete data 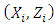 , the logarithm likelihood function is explicitly given by
, the logarithm likelihood function is explicitly given by 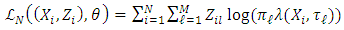
 where
where 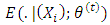 is the conditional expectation given
is the conditional expectation given  computed with the distribution of the complete data under the value
computed with the distribution of the complete data under the value 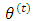 of the parameter, and the maximization (M) step computes parameters that maximize the expected log-likelihood found on the (E) step
of the parameter, and the maximization (M) step computes parameters that maximize the expected log-likelihood found on the (E) step 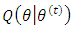 . In the (E) step, we compute
. In the (E) step, we compute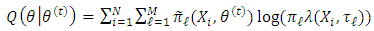 where
where  is the posterior probability
is the posterior probability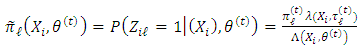
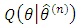 with respect to
with respect to 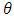 , where
, where 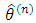 is the current value of parameter
is the current value of parameter  . We can maximize the terms that contain
. We can maximize the terms that contain 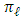 and
and 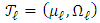 separately. We introduce one Lagrange multiplier
separately. We introduce one Lagrange multiplier 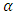 to maximize with respect to
to maximize with respect to  with the constraint
with the constraint  and solve the following equation:
and solve the following equation: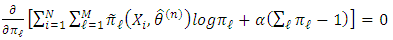 And the classical solution:
And the classical solution: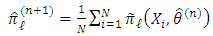 Then, we maximize
Then, we maximize 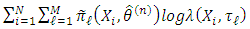 , where the derivatives can be computed with respect to the components of
, where the derivatives can be computed with respect to the components of 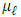 and
and 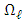 by using some results from matrix algebra. When taking the log of
by using some results from matrix algebra. When taking the log of 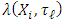 , substituting it into
, substituting it into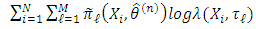 , and taking the derivative w.r.t.
, and taking the derivative w.r.t. 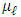 , we have
, we have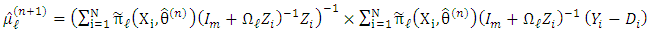
 are known and when the
are known and when the  are unknown, the maximum likelihood estimators of the parameters are given by the system.Proposition 3.1 The sequence
are unknown, the maximum likelihood estimators of the parameters are given by the system.Proposition 3.1 The sequence  generated by the EM algorithm converges to a stationary point of the likelihood.Proof. We prove the convergence for
generated by the EM algorithm converges to a stationary point of the likelihood.Proof. We prove the convergence for  to avoid cumbersome details. We employ the results obtained by McLachlan and Krishnan [15]. As the following conditions are given:
to avoid cumbersome details. We employ the results obtained by McLachlan and Krishnan [15]. As the following conditions are given:  Conditions 3, 4, 5, and 6 are verified by the regularity of the likelihood (see Proposition 4.2). In a standard Gaussian mixture, condition 2 is usually unverified (see McLachlan and Krishnan [15]. However, here, one has the following result (see (12)):
Conditions 3, 4, 5, and 6 are verified by the regularity of the likelihood (see Proposition 4.2). In a standard Gaussian mixture, condition 2 is usually unverified (see McLachlan and Krishnan [15]. However, here, one has the following result (see (12)): Where
Where  . Therefore, the formula of
. Therefore, the formula of  is a mixture of Gaussian distributions that consist of variances all bounded from below. This finding reveals condition 2.
is a mixture of Gaussian distributions that consist of variances all bounded from below. This finding reveals condition 2. when we assume that the number of components M is known. For simplicity’s sake, we consider only the case
when we assume that the number of components M is known. For simplicity’s sake, we consider only the case  . The parameter set
. The parameter set 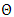 is given by
is given by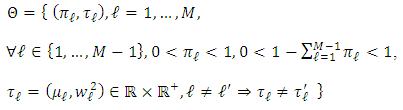 Now, we set
Now, we set 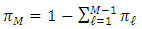 , but only
, but only 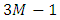 parameters need to be estimated. When necessary in notations, we set
parameters need to be estimated. When necessary in notations, we set 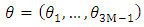 . The MLE is defined as any solution of
. The MLE is defined as any solution of where
where  is defined by (7)–(11). To prove the identifiability property, the following assumption is required as in Alkreemawi et al. [2]:(H4) Either the function
is defined by (7)–(11). To prove the identifiability property, the following assumption is required as in Alkreemawi et al. [2]:(H4) Either the function  is constant or not constant, and under
is constant or not constant, and under 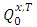 , the random variable
, the random variable 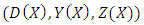 admits a density
admits a density 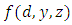 with respect to the Lebesgue measure on
with respect to the Lebesgue measure on 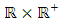 , which is jointly continuous and positive on an open ball of
, which is jointly continuous and positive on an open ball of 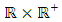 .When
.When 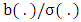 is constant, this case is simple. For instance, let
is constant, this case is simple. For instance, let 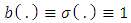 . Then,
. Then, 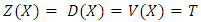 is deterministic, and under
is deterministic, and under 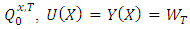 . Under
. Under is a mixture of Gaussian distributions with means
is a mixture of Gaussian distributions with means 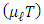 , variances
, variances 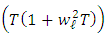 , and proportions
, and proportions 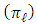 .The case where
.The case where 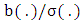 is not constant. Under smoothness assumptions on functions
is not constant. Under smoothness assumptions on functions  , assumption (H4) will be accomplished by using Malliavin calculus tools (see Alkreemawi et al. [2]). As mixture distributions are utilized, the identifiability of the entire parameter
, assumption (H4) will be accomplished by using Malliavin calculus tools (see Alkreemawi et al. [2]). As mixture distributions are utilized, the identifiability of the entire parameter  can only be obtained in the following concept:
can only be obtained in the following concept: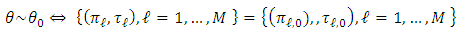
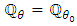 implies that
implies that  .Proof. First, when
.Proof. First, when 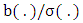 is not constant, we consider two parameters
is not constant, we consider two parameters 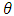 and
and 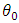 , and aim to prove that
, and aim to prove that  implies
implies  . As
. As 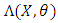 and
and 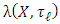 depend on
depend on 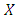 only through the statistics
only through the statistics 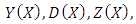
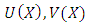 with a slight abuse of notation, we set
with a slight abuse of notation, we set 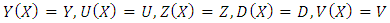 and
and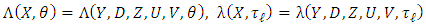
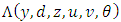 is the density of the distribution of
is the density of the distribution of  under
under 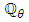 with respect to the density of
with respect to the density of 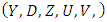 under
under  and
and 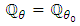 implies
implies  a.e., hence, everywhere on
a.e., hence, everywhere on  by the continuity assumption. We deduce that the following equality holds for all
by the continuity assumption. We deduce that the following equality holds for all 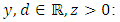
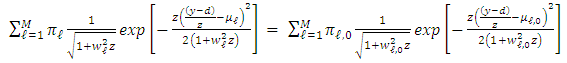 Let us set
Let us set and
and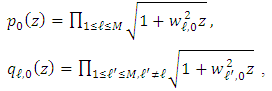 We note that
We note that  . Thus, such quantities do not depend on
. Thus, such quantities do not depend on 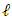 . After reducing to the same denominator, we obtain
. After reducing to the same denominator, we obtain The right-hand side is a function of
The right-hand side is a function of 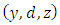 , whereas the left-hand side is a function of z only. This approach is possible only if
, whereas the left-hand side is a function of z only. This approach is possible only if 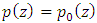 for all
for all  . Therefore,
. Therefore, 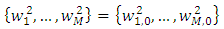
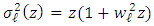 and a fixed z,
and a fixed z,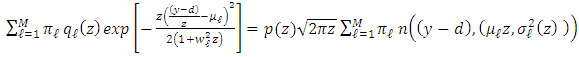
 indicates the Gaussian density with mean m and variance
indicates the Gaussian density with mean m and variance  . Analogously, by using the equality (18),
. Analogously, by using the equality (18),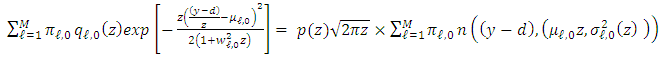 For all fixed
For all fixed 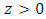 , we therefore have for all
, we therefore have for all 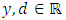 ,
, 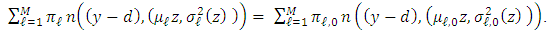 Herein, the equality of two mixtures of Gaussian distributions with proportions
Herein, the equality of two mixtures of Gaussian distributions with proportions 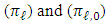 , expectations
, expectations  and
and 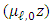 , and the same set of known variances
, and the same set of known variances 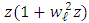 are given. From the identifiability of Gaussian mixtures, we have the equality
are given. From the identifiability of Gaussian mixtures, we have the equality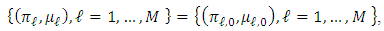 and thus,
and thus, 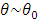 .Second, when
.Second, when  is constant, for instance, let
is constant, for instance, let 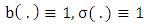 . As noted above, under
. As noted above, under 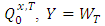 and
and 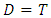 . Therefore,
. Therefore, 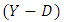 is a Gaussian distribution. Under
is a Gaussian distribution. Under  ,
,  has density
has density 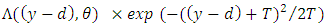 w. r. t. the Lebesgue measure on
w. r. t. the Lebesgue measure on 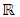 . Specifically, the mixture of Gaussian densities can also be deduced based on the identifiability property of Gaussian mixtures.Proposition 4.2. Let
. Specifically, the mixture of Gaussian densities can also be deduced based on the identifiability property of Gaussian mixtures.Proposition 4.2. Let  denote the expectation under
denote the expectation under 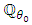 . The function
. The function  is
is 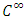 on
on  and
and 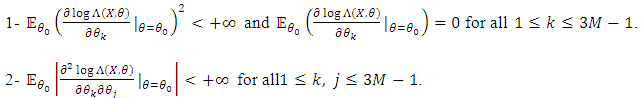
 for all
for all 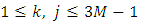 .The Fisher information matrix can be defined as
.The Fisher information matrix can be defined as 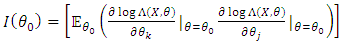 for all
for all 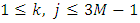 . Proof. We use results proved in Alkreemawi el al. [2] (Section 3.1, Lemma 3.1.1, Proposition 3.1.2) to prove this proposition. For all
. Proof. We use results proved in Alkreemawi el al. [2] (Section 3.1, Lemma 3.1.1, Proposition 3.1.2) to prove this proposition. For all 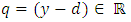 and all
and all  ,
,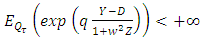
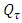 is the distribution of
is the distribution of 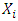 when
when 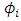 has a Gaussian distribution with parameters
has a Gaussian distribution with parameters 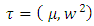 . This idea implies that
. This idea implies that 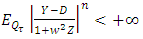 for all
for all  . Let
. Let The random variable that has moments of any order under
The random variable that has moments of any order under  is bounded, and the following relations hold:
is bounded, and the following relations hold: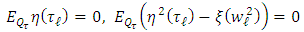
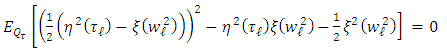
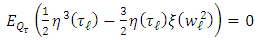
 are well defined. For
are well defined. For  , we have
, we have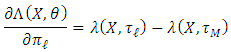 As for all
As for all 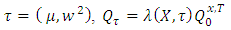 , the random variable above is
, the random variable above is 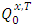 -integrable and
-integrable and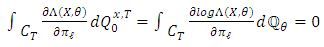 Moreover, as
Moreover, as 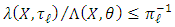 , we have
, we have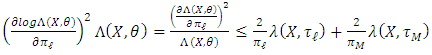 Therefore,
Therefore, 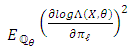
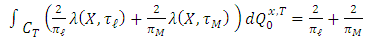 Higher order derivatives of
Higher order derivatives of 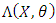 with respect to the
with respect to the 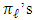 are nul:
are nul: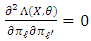 Now we find the derivatives with respect to the parameters
Now we find the derivatives with respect to the parameters 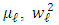 . We have:
. We have: 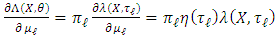 We know that:
We know that: 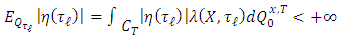
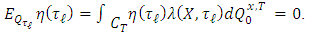 Consequently,
Consequently,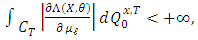
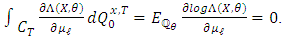 Now,
Now,  Thus,
Thus,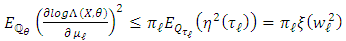 Next, we have
Next, we have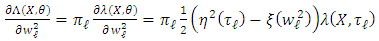 Again, we know that this random variable is
Again, we know that this random variable is  -integrable with nul integral, thereby obtaining
-integrable with nul integral, thereby obtaining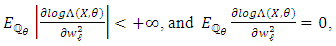 Moreover,
Moreover,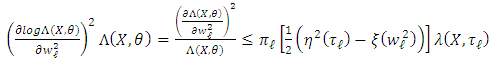 This finding implies that
This finding implies that Now we look at second-order derivatives. The successive derivatives with respect to
Now we look at second-order derivatives. The successive derivatives with respect to 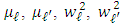 with
with 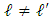 are nul. We obtain
are nul. We obtain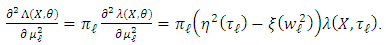 This random variable is integrable with respect to
This random variable is integrable with respect to  with the nul integral. Thus,
with the nul integral. Thus,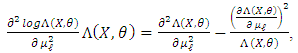 We find that this random variable is integrable with respect to
We find that this random variable is integrable with respect to  , and computing the integral obtains
, and computing the integral obtains 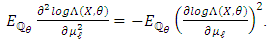 Next,
Next,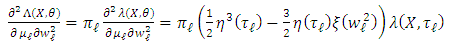
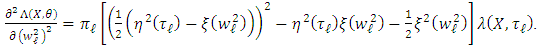 Thus, we conclude the proof analogously using (21) and (22).Proposition 4.3. Assume that
Thus, we conclude the proof analogously using (21) and (22).Proposition 4.3. Assume that 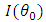 is invertible and (H1)–(H2). Then, an estimator
is invertible and (H1)–(H2). Then, an estimator 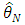 solves the likelihood estimating equation
solves the likelihood estimating equation  with a probability tending to 1 and
with a probability tending to 1 and 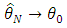 in probability.Proof. For weak consistency following the standard steps, the uniformity condition needs to be proven. We prove that An open convex subset
in probability.Proof. For weak consistency following the standard steps, the uniformity condition needs to be proven. We prove that An open convex subset 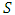 of
of  exists, which contains
exists, which contains  and functions
and functions 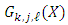 such that, on S,
such that, on S,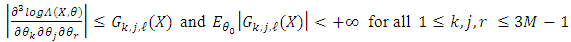 .
.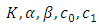 are set as positive numbers such that
are set as positive numbers such that 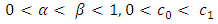 , and
, and 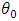 is assumed to belong to
is assumed to belong to  where
where  . We have to study
. We have to study 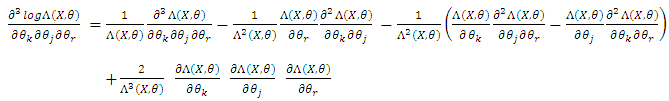 Therefore, we have, for
Therefore, we have, for 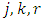 distinct indexes
distinct indexes As
As  ,
, We use
We use 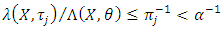 again to bound the other third-order derivatives. Then, in the derivatives, random variables appear
again to bound the other third-order derivatives. Then, in the derivatives, random variables appear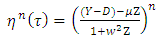 for different values of n. We now bound
for different values of n. We now bound 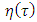 by an r. v. independent of
by an r. v. independent of  and have moments of any order under
and have moments of any order under 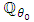 . We have
. We have Thus,
Thus,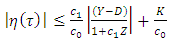 Now, in the same method
Now, in the same method 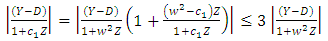 For all
For all 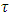 , this finding implies that
, this finding implies that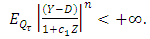 Consequently,
Consequently, The proof of Proposition 4.3 is complete.
The proof of Proposition 4.3 is complete.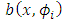 is linear in
is linear in  , where
, where  has a mixture of Gaussian. We obtain an expression of the exact likelihood. When the number of components is known, we prove the consistency of the maximum likelihood estimators (MLEs). Properties of the EM algorithm are described when the algorithm is used to compute MLE.
has a mixture of Gaussian. We obtain an expression of the exact likelihood. When the number of components is known, we prove the consistency of the maximum likelihood estimators (MLEs). Properties of the EM algorithm are described when the algorithm is used to compute MLE. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML