Chukwu A. U., Ogunde A. A.
Department of Statistics, University of Ibadan, Department of Mathematics and Statistics, Federal Polytechnic, Ado-Ekiti, Nigeria
Correspondence to: Ogunde A. A., Department of Statistics, University of Ibadan, Department of Mathematics and Statistics, Federal Polytechnic, Ado-Ekiti, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, a new five-parameter generalized version of the Gompertz-Makeham distribution called Kumaraswamy Gompertz-Makeham (KGM). The new distribution is quite flexible and can have a decreasing, increasing, and bathtub-shaped failure rate function depending on its parameters making it effective in modeling survival data and reliability problems. The maximum likelihood function of the new distribution was derived. Some comprehensive properties of the new distribution, such as closed-form expressions for the density, cumulative distribution, hazard rate function, the ith order statistics were provided. At the end, in order to show the capability of KGM over its sub models, an application to a real dataset illustrates its potentiality.
Keywords:
Kumaraswamy Gompertz-Makeham distribution, Maximum likelihood estimation, Bathtub-shaped failure rate
Cite this paper: Chukwu A. U., Ogunde A. A., On Kumaraswamy Gompertz Makeham Distribution, American Journal of Mathematics and Statistics, Vol. 6 No. 3, 2016, pp. 122-127. doi: 10.5923/j.ajms.20160603.06.
1. Introduction
Modelling of interrelationship among naturally occurring phenomena is made possible by the use of distribution function and their properties. Because of this, considerable effort has been expended in the development of large classes of standard probability distributions along with relevant statistical methodologies. The paper by Kumaraswamy proposed a new probability distribution for double bounded random processes with hydrological applications. This new family of distribution most especially its probability density function has been found to have the same properties as the beta distribution but has some advantages in terms of tractability.
2. Kumaraswamy Distribution
The kumaraswamy distribution on the interval (0,1) has the probability density function, 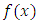 corresponding to (1) and cumulative distribution function,
corresponding to (1) and cumulative distribution function, 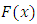 which takes the form (2) with two shape parameter ,
which takes the form (2) with two shape parameter ,  defined by,
defined by,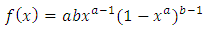 | (1) |
And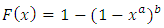 | (2) |
Combining the work of Eugene et al (2002) and Jones (2004) to construct a new class of kumaraswamy generalized (KwG) distribution can be obtained. From an arbitrary parent cumulative density function, F(x), the cumulative density function, 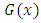 of the Kumaraswamy Generalized distribution is defined by
of the Kumaraswamy Generalized distribution is defined by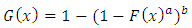 | (3) |
Where 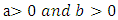 are two additional parameters whose role is to introduce Skewness and vary the tail weights. Because of its tractability, the kumaraswamy distribution function (Kw) distribution can be used quite effectively even if the data were censored.Correspondingly, the density function of this family has a very simple form given by
are two additional parameters whose role is to introduce Skewness and vary the tail weights. Because of its tractability, the kumaraswamy distribution function (Kw) distribution can be used quite effectively even if the data were censored.Correspondingly, the density function of this family has a very simple form given by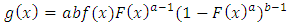 | (4) |
Several generalized distributions from (4) have been defined and investigated in the literature including the Kumaraswamy Weibull distribution by Cordeiro et al. (2010), the Kumaraswamy generalized gamma distribution by de Castro et al. (2011) and the Kumaraswamy generalized half-normal distribution by Cordeiro et al. (2012).
3. Verification of Kumaraswamy Distribution to be a Proper Pdf
We want to show that the integral 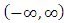 of the pdf of KGM distribution is equal to 1, that is
of the pdf of KGM distribution is equal to 1, that is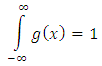 If we let
If we let 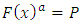 , implies that
, implies that 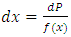 then equation 4 will transform to,
then equation 4 will transform to,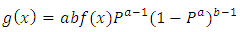 Then,
Then,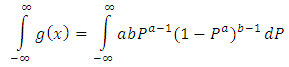 Further, we let
Further, we let 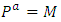 , then
, then 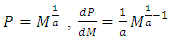 Therefore,
Therefore,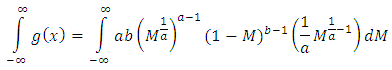 This implies that,
This implies that,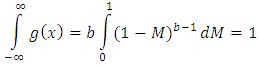 This verified that the probability density function of a kumaraswamy distribution function is indeed a proper pdf.
This verified that the probability density function of a kumaraswamy distribution function is indeed a proper pdf.
4. Gompertz Makeham Distribution
The Gompertz-Makeham law states that the death rate is the sum of an age independent component which increases exponentially with age and captures the age independent adult mortality. In a protected environment where external causes of death are rare (laboratory conditions, low mortality countries, etc.), the age-independent mortality component is often negligible. In this case the formula simplifies to a Gompertz law of mortality. In 1825, Benjamin Gompertz proposed an exponential increase in death rates with age.The Gompertz–Makeham model provides a better fit empirical mortality distribution between the ages 30 and 85 years (Finch 1990).A random variable X is distributed Gompertz-Makeham if and only its pdf satisfies the below 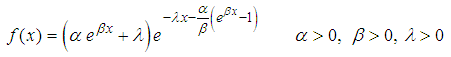 | (5) |
Its cumulative density function is 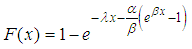 | (6) |
5. Kumaraswamy Gompertz Makeham Distributions (KGM)
Using (6) in (3), The CDF of kumaraswamy Gompertz Makeham distribution (KGM) can be obtained as follows: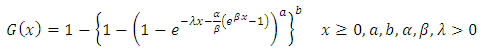 | (7) |
Also using (5) and (6) in (3) the probability density function of KGM can be obtained as: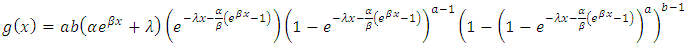 | (8) |
This can be simplified as: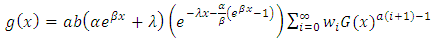 | (9) |
Taken, 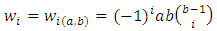
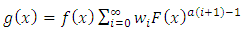 | (10) |
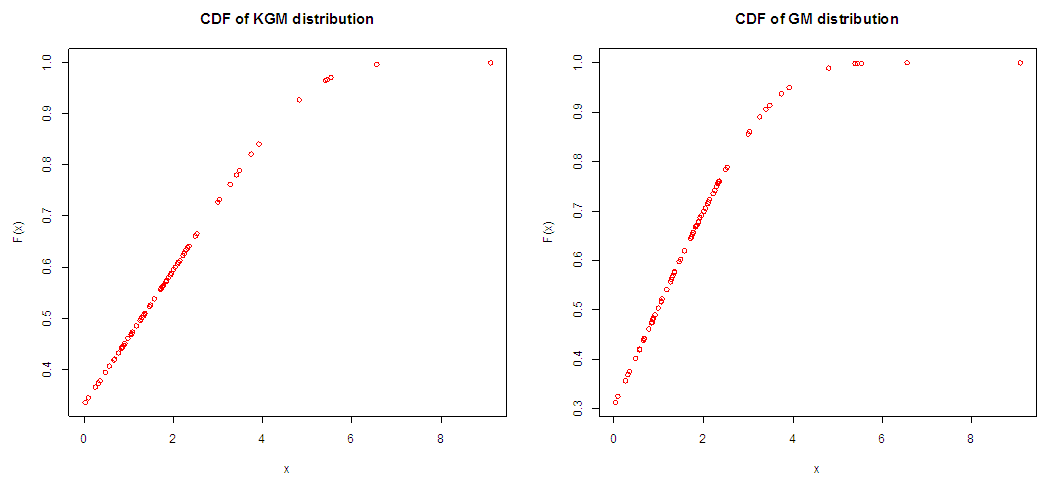
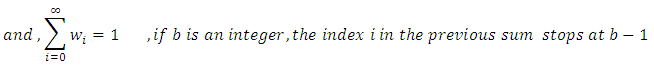 Figure (1) and (2) depict the behaviour of the distribution for some parameters values,
Figure (1) and (2) depict the behaviour of the distribution for some parameters values, 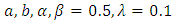 .The plot of probability density function and the Cumulative density function shows in the diagram above clearly indicates that the Kumaraswamy Gompertz Makeham distribution is more flexible than the Gompertz Makeham distribution.
.The plot of probability density function and the Cumulative density function shows in the diagram above clearly indicates that the Kumaraswamy Gompertz Makeham distribution is more flexible than the Gompertz Makeham distribution.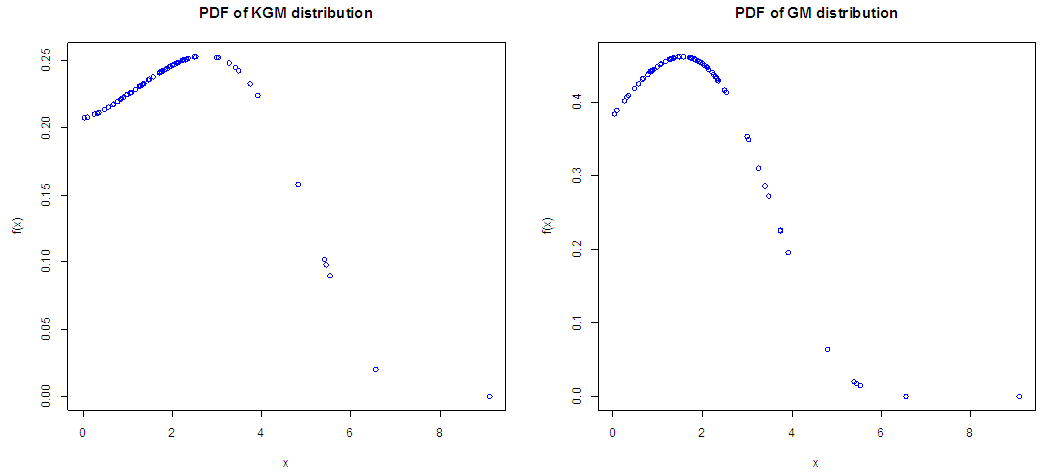 | Figure 1. |
 | Figure 2. |
6. Statistical Properties
Asymptotic BehaviorWe seek to investigate the behaviour of the model in equation (7),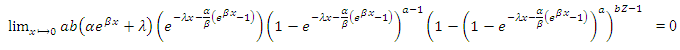
7. Hazard Rate Function
The hazard rate function can be obtained by using,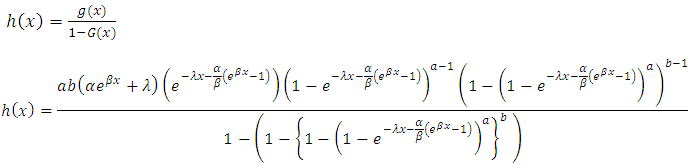 | (11) |
This can be simplified to obtain,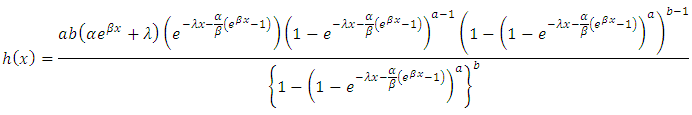 Which can be further reduced to,
Which can be further reduced to,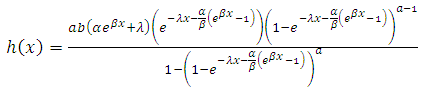 | (12) |
The equation (12) is the hazard of the kumaraswamy Gompertz distribution and also called the Kumaraswamy Gompertz Makeham Model.When the value of 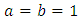 , we have,
, we have,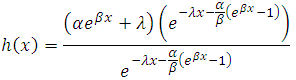 This gives,
This gives,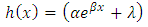 | (13) |
The above is the hazard of Gompertz Makeham distribution or Gompertz-Makeham model.
8. Reliability Function
The reliability of a function is defined by: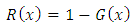 For Kumaraswamy Gompertz Makeham distribution, the Reliability function is given as,
For Kumaraswamy Gompertz Makeham distribution, the Reliability function is given as,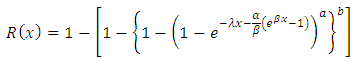 This can be simplified to obtain,For a kumaraswamy Gompertz Makeham distribution, the reliability function is,
This can be simplified to obtain,For a kumaraswamy Gompertz Makeham distribution, the reliability function is,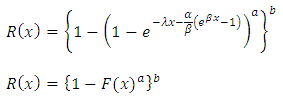 Therefore,
Therefore,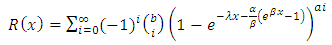 | (13) |
9. Order Statistics
Order statistics make their appearance in many areas of statistical theory and practice. The density 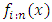 of the
of the 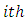 order statistics for
order statistics for 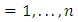 , from
, from 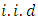 random variables
random variables 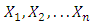 that follows any kumaraswamy generalized distribution is given by,
that follows any kumaraswamy generalized distribution is given by,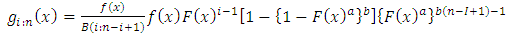 | (14) |
Considering equation 5 and 6, and let 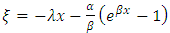 , will transform to:
, will transform to: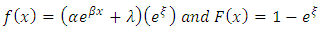 and inserting it in equation 12 we have,
and inserting it in equation 12 we have,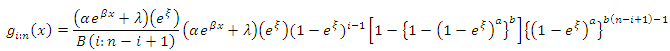
10. Estimation of Statistical Inference
Let 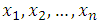 be random variable distributed according to (8) the likelihood function of a vector of parameters given as
be random variable distributed according to (8) the likelihood function of a vector of parameters given as 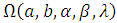 .Let
.Let 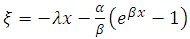
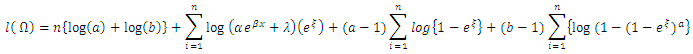 Then the score vector
Then the score vector 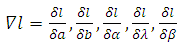 has components,
has components,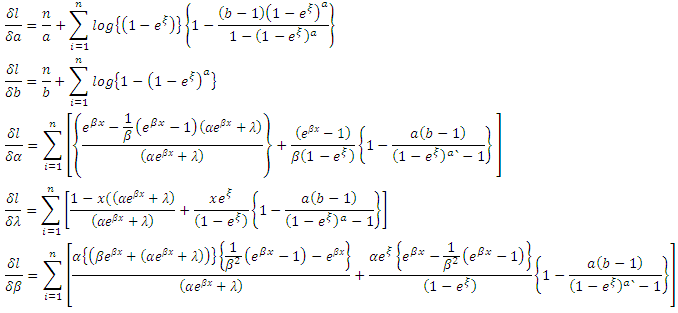
11. Application
To illustrate the new results presented in this paper, we fit the KGM distribution to an uncensored data set from Nichols and Padgett, (2006) considering 100 observations on breaking stress of carbon fibres (in Gba). The data are as follows : 3.7, 2.74, 2.73, 2.5, 3.6, 3.11, 3.27, 2.87, 1.47, 3.11,4.42, 2.41, 3.19, 3.22, 1.69, 3.28, 3.09, 1.87, 3.15, 4.9, 3.75, 2.43, 2.95, 2.97, 3.39, 2.96, 2.53,2.67, 2.93, 3.22, 3.39, 2.81, 4.2, 3.33, 2.55, 3.31, 3.31, 2.85, 2.56, 3.56, 3.15, 2.35, 2.55, 2.59,2.38, 2.81, 2.77, 2.17, 2.83, 1.92, 1.41, 3.68, 2.97, 1.36, 0.98, 2.76, 4.91, 3.68, 1.84, 1.59,3.19,1.57, 0.81, 5.56, 1.73, 1.59, 2, 1.22, 1.12, 1.71, 2.17, 1.17, 5.08, 2.48, 1.18, 3.51, 2.17, 1.69,1.25, 4.38, 1.84, 0.39, 3.68, 2.48, 0.85, 1.61, 2.79, 4.7, 2.03, 1.8, 1.57, 1.08, 2.03, 1.61, 2.12,1.89, 2.88, 2.82, 2.05, 3.65.These data were previously studied by Souza et al. (2011) for beta Frechet (BF), exponentiated Frechet (EF) and Frechet distributions. In the following, we shall compare the proposed KGM and its sub-model (GM) with several other three- and four-parameter lifetime distributions, namely: the Zografos-Balakrishnan log-logistic (ZBLL) (Zografos and Balakrishnan, 2009), the beta Frechet (BF) (Nadarajah and Gupta, 2004 and Souza et al., 2011) and recently the Kumaraswamy Pareto (KP) (Bourguignon et al., 2013) models with corresponding densities: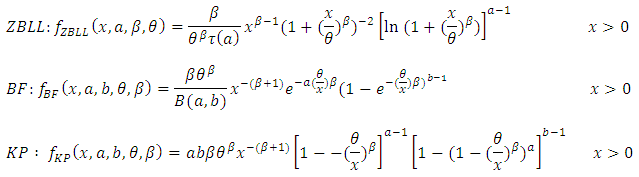 Where
Where 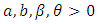 Table 1 gives the descriptive statistics of the data and Table 2 lists the MLEs of the model parameters for KGM, GM, BF, KP, ZBLL, BF and EF distributions, the corresponding errors(given in parenthesis) and the statistics
Table 1 gives the descriptive statistics of the data and Table 2 lists the MLEs of the model parameters for KGM, GM, BF, KP, ZBLL, BF and EF distributions, the corresponding errors(given in parenthesis) and the statistics 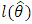 (where
(where 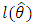 denotes the log-likelihood function evaluated at the maximum likelihood estimates), Akaike information criterion (AIC), the Bayesian information criterion (BIC), Consistent Akaike information criterion (CAIC) and Hannan-Quinn information criterion (HQIC). Since the KGM distribution has the lowest
denotes the log-likelihood function evaluated at the maximum likelihood estimates), Akaike information criterion (AIC), the Bayesian information criterion (BIC), Consistent Akaike information criterion (CAIC) and Hannan-Quinn information criterion (HQIC). Since the KGM distribution has the lowest 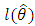 , AIC, BIC, CAIC and HQIC values among all other models and so it could be chosen as the best model.
, AIC, BIC, CAIC and HQIC values among all other models and so it could be chosen as the best model. | Table 1. Descriptive Statistics on Breaking stress of Carbon fibres |
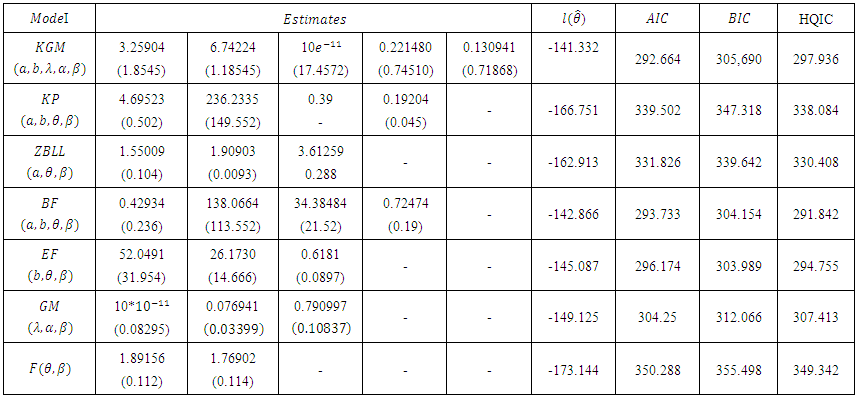 | Table 2. MLEs (standard error in parenthesis) and the statistics 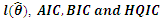 |
References
| [1] | Cordeiro, G.M. and M. de Castro, 2010. A new family of generalized distributions. Journal of Statistical Computation and Simulation, 81: 883-898. |
| [2] | Cordeiro, G.M., E.M.M. Ortega and S. Nadarajah, 2010. The Kumaraswamy Weibull distribution with application to failure data. J. Frankl. Inst., 347: 1399-1429. |
| [3] | Chukwu A.U. & Ogunde A. A. (2015), 'On the Beta Makeham Distribution and its Applications', American Journal of Mathematics and Statistics 2015, 5(3): 137-143 |
| [4] | El-Gohary, A. & Al-Otaibi, A. N. (2013), ‘The generalized Gompertz distribution’, Applied Mathematical Modeling 37(1-2), 13–24. |
| [5] | Ohishi, K., Okamura, H. & Dohi, T. (2009), ‘Gompertz software reliability model: Estimation algorithm and empirical validation’, Journal of Systems and Software 82(3), 535–543. |
| [6] | Willemse, W. & Koppelaar, H. (2000), ‘Knowledge elicitation of Gompertz’ law of mortality’, Scandinavian Actuarial Journal 2, 168–179. |
| [7] | Strecher, B.L (1960). Fluctuating energy demands as determinants of the death process (parsimonious theory of the Gompertz function). In ‘’The Biology of Aging’’ (B.L Stretchers et al., eds.) pp. 309-314 Publ. No.6,Am. Inst. Biology Science, Washington. |
| [8] | Sanderson, W. (1995) Predictability, complexity and catastrophe in a collapsible model of population, development and environmental interactions. Mathematical Population studies 5:233-279. |
| [9] | Gompertz, B. (1825), ‘’on the Nature of function Expressive of the Law of Human Mortality, and on a new mode of determining the value of life contingencies’’. Philosophical Transaction of the Royal Society of London 115:513583. |
| [10] | Nadarajah, S. and S. Kotz, 2003. The exponentiated Fréchet distribution. Available at Interstat. statjournals net, 0312001. |
| [11] | Nichols, M.D. and W. J. Padgett, 2006. A bootstrap control chart for Weibull Percentiles. Quality and Reliability Engineering International, 22: 141-151. |
| [12] | Smith, R.L. and J.C. Naylor, 1987. A comparison of maximum likelihood and Bayesian estimators for the three-parameter Weibull distribution. Applied Statistics, 36: 358-369. |
| [13] | Shahbaz, M.Q., S. Shahbaz and N.S. Butt, 2012. The Kumaraswamy inverse Weibull distribution. Pakistan Journal of Statistics and Operation Research, 8: 479-489. |
| [14] | Souza, W.M., G.M. Cordeiro and A.B. Simas, 2011. Some results for beta Fréchet distribution. Commun. Statist. Theory-Meth., 40: 798-811. |
| [15] | Zografos, K. and N. Balakrishnan, 2009. On families of beta- and generalized gamma-generated distributions and associated inference. Stat. Method., 6: 344-362. |



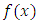 corresponding to (1) and cumulative distribution function,
corresponding to (1) and cumulative distribution function, 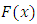 which takes the form (2) with two shape parameter ,
which takes the form (2) with two shape parameter , 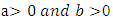 defined by,
defined by,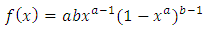
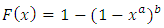
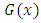 of the Kumaraswamy Generalized distribution is defined by
of the Kumaraswamy Generalized distribution is defined by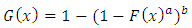
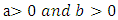 are two additional parameters whose role is to introduce Skewness and vary the tail weights. Because of its tractability, the kumaraswamy distribution function (Kw) distribution can be used quite effectively even if the data were censored.Correspondingly, the density function of this family has a very simple form given by
are two additional parameters whose role is to introduce Skewness and vary the tail weights. Because of its tractability, the kumaraswamy distribution function (Kw) distribution can be used quite effectively even if the data were censored.Correspondingly, the density function of this family has a very simple form given by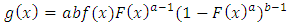
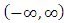 of the pdf of KGM distribution is equal to 1, that is
of the pdf of KGM distribution is equal to 1, that is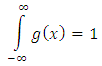 If we let
If we let 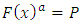 , implies that
, implies that 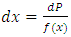 then equation 4 will transform to,
then equation 4 will transform to,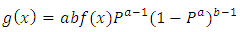 Then,
Then,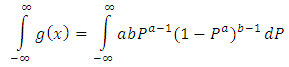 Further, we let
Further, we let 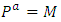 , then
, then 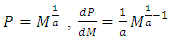 Therefore,
Therefore,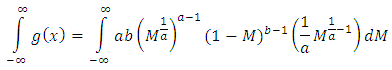 This implies that,
This implies that,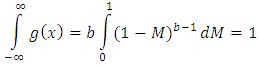 This verified that the probability density function of a kumaraswamy distribution function is indeed a proper pdf.
This verified that the probability density function of a kumaraswamy distribution function is indeed a proper pdf.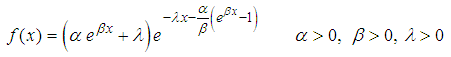
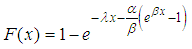
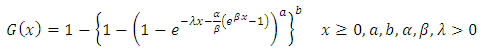
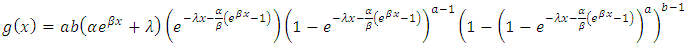
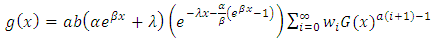
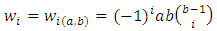
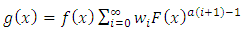
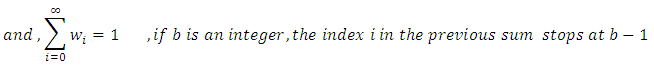 Figure (1) and (2) depict the behaviour of the distribution for some parameters values,
Figure (1) and (2) depict the behaviour of the distribution for some parameters values, 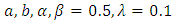 .The plot of probability density function and the Cumulative density function shows in the diagram above clearly indicates that the Kumaraswamy Gompertz Makeham distribution is more flexible than the Gompertz Makeham distribution.
.The plot of probability density function and the Cumulative density function shows in the diagram above clearly indicates that the Kumaraswamy Gompertz Makeham distribution is more flexible than the Gompertz Makeham distribution.

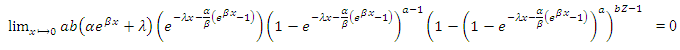
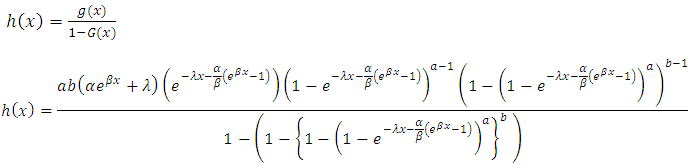
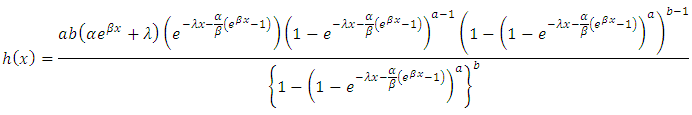 Which can be further reduced to,
Which can be further reduced to,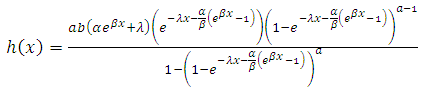
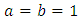 , we have,
, we have,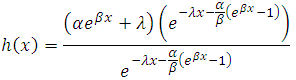 This gives,
This gives,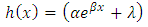
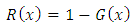 For Kumaraswamy Gompertz Makeham distribution, the Reliability function is given as,
For Kumaraswamy Gompertz Makeham distribution, the Reliability function is given as,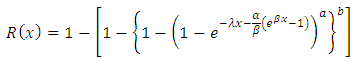 This can be simplified to obtain,For a kumaraswamy Gompertz Makeham distribution, the reliability function is,
This can be simplified to obtain,For a kumaraswamy Gompertz Makeham distribution, the reliability function is,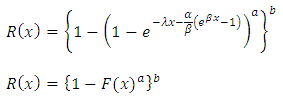 Therefore,
Therefore,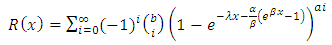
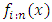 of the
of the 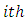 order statistics for
order statistics for 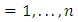 , from
, from 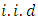 random variables
random variables 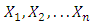 that follows any kumaraswamy generalized distribution is given by,
that follows any kumaraswamy generalized distribution is given by,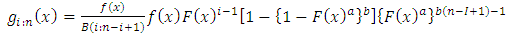
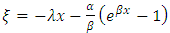 , will transform to:
, will transform to: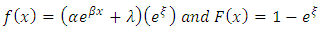 and inserting it in equation 12 we have,
and inserting it in equation 12 we have,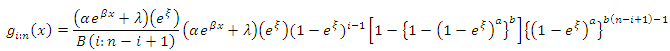
 be random variable distributed according to (8) the likelihood function of a vector of parameters given as
be random variable distributed according to (8) the likelihood function of a vector of parameters given as 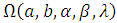 .Let
.Let 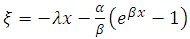
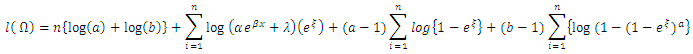 Then the score vector
Then the score vector 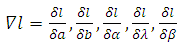 has components,
has components,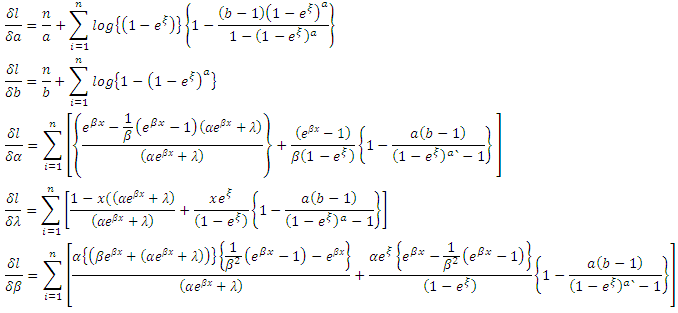
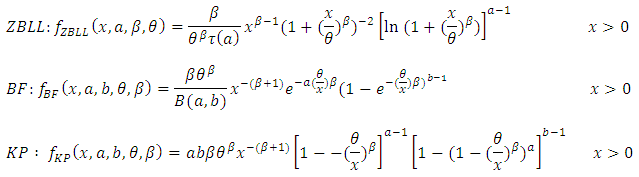 Where
Where  Table 1 gives the descriptive statistics of the data and Table 2 lists the MLEs of the model parameters for KGM, GM, BF, KP, ZBLL, BF and EF distributions, the corresponding errors(given in parenthesis) and the statistics
Table 1 gives the descriptive statistics of the data and Table 2 lists the MLEs of the model parameters for KGM, GM, BF, KP, ZBLL, BF and EF distributions, the corresponding errors(given in parenthesis) and the statistics  (where
(where 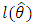 denotes the log-likelihood function evaluated at the maximum likelihood estimates), Akaike information criterion (AIC), the Bayesian information criterion (BIC), Consistent Akaike information criterion (CAIC) and Hannan-Quinn information criterion (HQIC). Since the KGM distribution has the lowest
denotes the log-likelihood function evaluated at the maximum likelihood estimates), Akaike information criterion (AIC), the Bayesian information criterion (BIC), Consistent Akaike information criterion (CAIC) and Hannan-Quinn information criterion (HQIC). Since the KGM distribution has the lowest 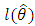 , AIC, BIC, CAIC and HQIC values among all other models and so it could be chosen as the best model.
, AIC, BIC, CAIC and HQIC values among all other models and so it could be chosen as the best model.

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML