-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2016; 6(3): 103-107
doi:10.5923/j.ajms.20160603.03

Class of Estimators of Population Mode Using New Parametric Relationship for Mode
Mukesh K. Sharma, Sarbjit S. Brar, Harinder Kaur
Department of Statistics, Punjabi University, Patiala, India
Correspondence to: Sarbjit S. Brar, Department of Statistics, Punjabi University, Patiala, India.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

For estimating the population mode using the known information of population mean 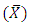 of the auxiliary variable, a class of estimators has been proposed by making use of new parametric relationship for mode developed by Sharma et.al. (2016). We have derived the asymptotic expression for the bias and MSE of any estimators of the proposed class and also obtain the minimum MSE in the proposed class. The results are also illustrated numerically.
of the auxiliary variable, a class of estimators has been proposed by making use of new parametric relationship for mode developed by Sharma et.al. (2016). We have derived the asymptotic expression for the bias and MSE of any estimators of the proposed class and also obtain the minimum MSE in the proposed class. The results are also illustrated numerically.
Keywords: Mode, Skewness, Auxiliary variable, Bias and Mean square error, Bivariate normal distribution
Cite this paper: Mukesh K. Sharma, Sarbjit S. Brar, Harinder Kaur, Class of Estimators of Population Mode Using New Parametric Relationship for Mode, American Journal of Mathematics and Statistics, Vol. 6 No. 3, 2016, pp. 103-107. doi: 10.5923/j.ajms.20160603.03.
Article Outline
1. Introduction
- In many practical situations, the more appropriate measure of location is mode rather than mean and median. For example, it is useful in finding the ideal size as in studies relating to marketing, trade and industry and also to find the ideal size such as in the manufacturing of shoes or ready-made garments, etc. In addition, the mode is also useful when dealing with skewed distributions such as income, drugs, AIDS etc. The impact of the proposed research is expected to be useful for scientists in Sociology, Psychology, Demography, Business and Economics, where the mode value is routinely being used in practice. Sharma et al (2016) established the new parametric relationship for population mode
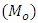 as
as 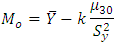 where
where 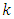 is unknown constant to be determined for the given population. They proposed three estimators of
is unknown constant to be determined for the given population. They proposed three estimators of 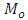 under the different situations as
under the different situations as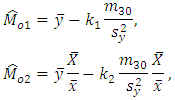 and
and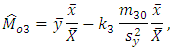 Where
Where 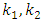 and
and 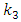 are unknown constants, whose values are determined by minimizing the MSE’s of respective estimators
are unknown constants, whose values are determined by minimizing the MSE’s of respective estimators 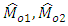 and
and 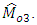 Here the estimator
Here the estimator 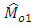 uses no information on auxiliary variable
uses no information on auxiliary variable 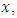 which is highly correlated with
which is highly correlated with 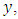 whereas
whereas 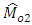 and
and 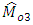 uses the known information of
uses the known information of 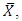 which are of ratio and product type estimators respectively.In the present paper, we propose a class of estimators of population mode using the new parametric relationship for population mode when the population mean
which are of ratio and product type estimators respectively.In the present paper, we propose a class of estimators of population mode using the new parametric relationship for population mode when the population mean 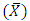 of the auxiliary variable is known. Asymptotic expression for the bias and MSE of any estimators of the proposed class and also their minimum values are obtained upto to terms of order
of the auxiliary variable is known. Asymptotic expression for the bias and MSE of any estimators of the proposed class and also their minimum values are obtained upto to terms of order 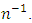 The results are also illustrated numerically.
The results are also illustrated numerically.2. Notations and Expectations
- Let a simple random sample of size
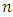 is drawn from a population of size
is drawn from a population of size 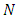 by using simple random sampling without replacement (SRSWOR). Without loss of generality, we ignore the finite population correction (fpc) throughout the paper.Let
by using simple random sampling without replacement (SRSWOR). Without loss of generality, we ignore the finite population correction (fpc) throughout the paper.Let 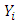 and
and 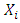 be the values of study and auxiliary variables for
be the values of study and auxiliary variables for 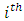 unit in the population respectively and the corresponding small letters
unit in the population respectively and the corresponding small letters 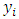 and
and 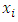 denote the sample values.Taking,
denote the sample values.Taking,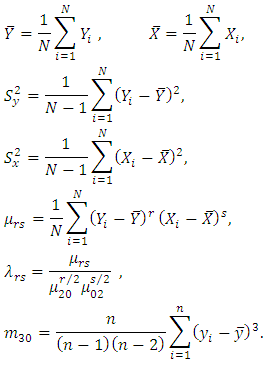 Obviously
Obviously Defining,
Defining,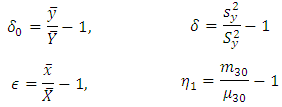 For the given SRSWOR, we have the following expectations,
For the given SRSWOR, we have the following expectations,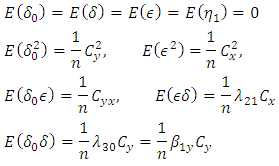 and up to terms of order
and up to terms of order 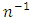
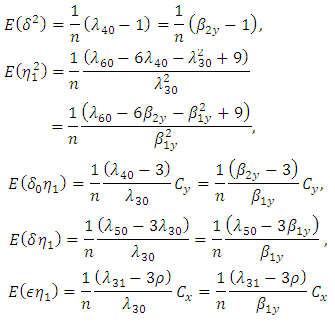
3. Proposed Class of Estimators
- In this section, we generalize the mean per unit, ratio-type and product-type estimators of population mode
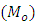 given by Sharma et al. (2016).Whatever be the sample chosen, let
given by Sharma et al. (2016).Whatever be the sample chosen, let 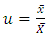 assume values in a bounded closed convex subset
assume values in a bounded closed convex subset 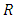 of the one-dimensional real space containing the value ‘1’. Let
of the one-dimensional real space containing the value ‘1’. Let 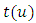 be a function of
be a function of 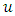 such that
such that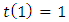 and it satisfies the following conditions:(i) The function
and it satisfies the following conditions:(i) The function 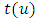 is continuous and bounded in
is continuous and bounded in 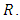 (ii) The first and second order partial derivatives of
(ii) The first and second order partial derivatives of 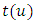 exist and are continuous and bounded in
exist and are continuous and bounded in 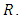 We propose the class of estimator of the population mode
We propose the class of estimator of the population mode 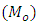 as
as 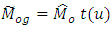 | (3.1) |
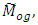 we expand the function
we expand the function 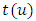 about the value ‘1’ in second-order Taylor’s series, we get
about the value ‘1’ in second-order Taylor’s series, we get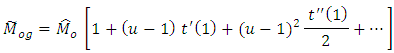 where
where 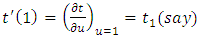 and
and 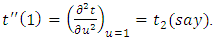 After writing the above function in terms of
After writing the above function in terms of 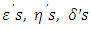 and then taking the expectations given in section 2, upto terms of order
and then taking the expectations given in section 2, upto terms of order 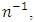 we get,
we get,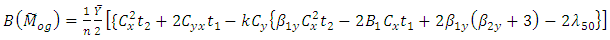 | (3.2) |
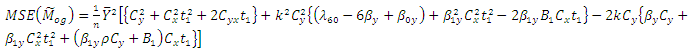 | (3.3) |
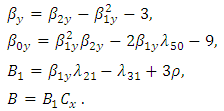 Here
Here 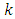 and
and 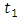 are unknown constants whose values are determined by minimizing
are unknown constants whose values are determined by minimizing 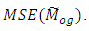 To obtain the minimum value of
To obtain the minimum value of 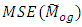 we differentiate (3.3) w.r.t.
we differentiate (3.3) w.r.t. 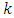 and
and 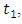 then equating to zero, we get,
then equating to zero, we get,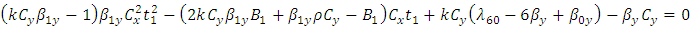 and
and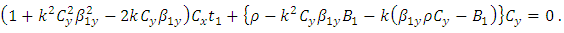 Solving above quadratic equations for
Solving above quadratic equations for 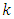 and
and 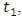 we get two pairs of solutions
we get two pairs of solutions 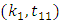 and
and 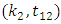 where,
where, 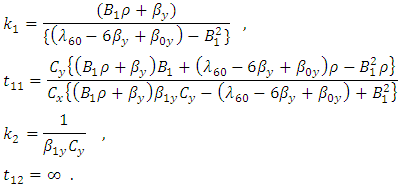 Clearly, the only feasible pair of values is
Clearly, the only feasible pair of values is 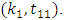 Substituting the values of pair
Substituting the values of pair 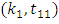 in (3.3), we get,
in (3.3), we get,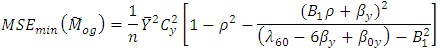 We can construct the large number of estimators belonging to the proposed class
We can construct the large number of estimators belonging to the proposed class 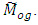 Here it should be noted that the efficient use of estimators of the proposed class
Here it should be noted that the efficient use of estimators of the proposed class 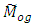 requires the optimum values of constants
requires the optimum values of constants 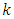 and
and 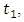 which are further functions of unknown population parameters. However, if it is possible to guess accurately the values of such parameters either through past experience or through a pilot sample survey and the value of optimum constants so obtained by using these guessed values of parameters are close enough to the optimum values of constants, then the resulting estimators will be better than the convention estimators. Srivastava and Jhajj (1983) have shown that upto the first order of approximation, the estimators of the class with estimated values of optimum parameters obtained by their respective consistent estimators, attain the same optimum MSE of class based on optimum values upto the first order of approximation. Therefore, the presence of unknown population parameters in optimum values of constants will not create any problem for practical use of the proposed class
which are further functions of unknown population parameters. However, if it is possible to guess accurately the values of such parameters either through past experience or through a pilot sample survey and the value of optimum constants so obtained by using these guessed values of parameters are close enough to the optimum values of constants, then the resulting estimators will be better than the convention estimators. Srivastava and Jhajj (1983) have shown that upto the first order of approximation, the estimators of the class with estimated values of optimum parameters obtained by their respective consistent estimators, attain the same optimum MSE of class based on optimum values upto the first order of approximation. Therefore, the presence of unknown population parameters in optimum values of constants will not create any problem for practical use of the proposed class 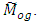
3.1. Special Case of Bivariate Normal Population
- Let
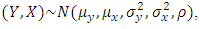 then we have
then we have 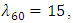
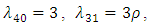
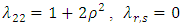 if
if 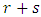 is odd. Also,
is odd. Also, 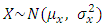 and
and 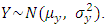 Using these values, we get,
Using these values, we get,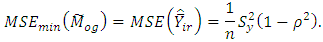
4. Numerical Illustrations
- To illustrate the result numerically, we have made computations for 12 populations taken from literature by using Microsoft Excel 2010.The source of the populations, the nature of the variables, the values of
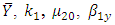 and
and 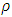 are listed in Table 1.
are listed in Table 1.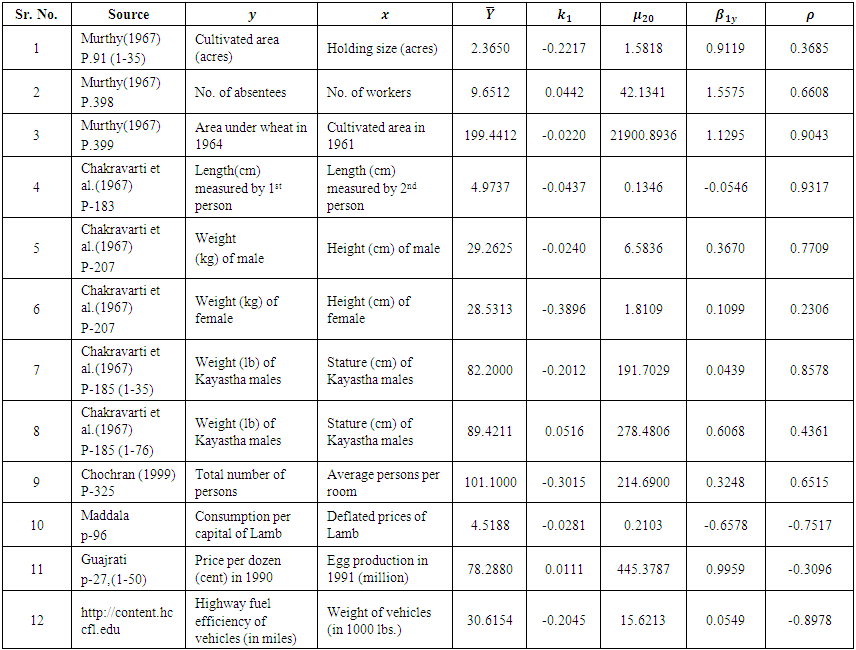 | Table 1. Description of populations |
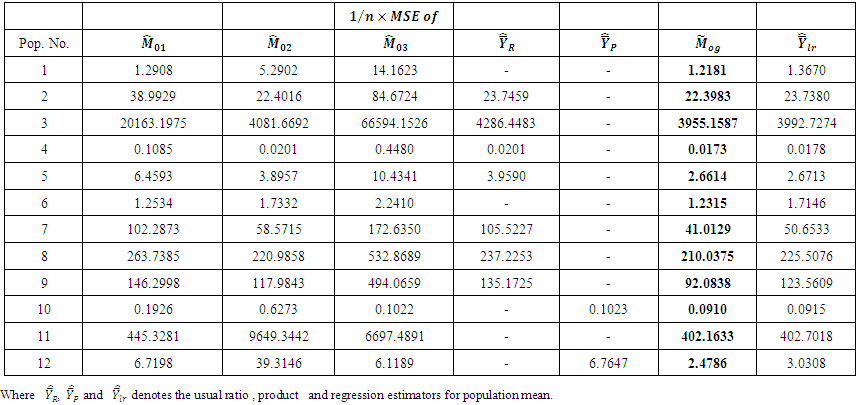 | Table 2. MSE’s of 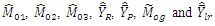 up to terms of up to terms of 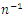 |
 is less than
is less than 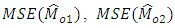 and
and 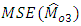 which implies that the proposed estimator is more efficient than the existing ones. Further,
which implies that the proposed estimator is more efficient than the existing ones. Further, 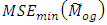 is also smaller than
is also smaller than 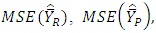
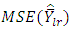 which shows that at optimum value of
which shows that at optimum value of 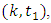 the proposed class estimators is more stable than the
the proposed class estimators is more stable than the 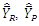 and
and 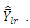
5. Conclusions
- A general class of estimators of population mode has been proposed and the lower bound for the MSE has been obtained for the class of estimators. Further, the empirical study shows that
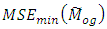 is less than
is less than 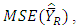
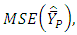
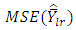 which implies that the optimum estimator is more stable than
which implies that the optimum estimator is more stable than 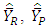 and
and 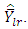
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML