-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2016; 6(3): 89-93
doi:10.5923/j.ajms.20160603.01

Vague Congruence Relation Induced by VLI – Ideals of Lattice Implication Algebras
T. Anitha1, V. Amarendra Babu2
1Department of Mathematics, K.L.University, Vaddeswaram, Guntur, India
2Department of Mathematics, Acharya Nagarjuna University, Nagarjuna Nagar, India
Correspondence to: T. Anitha, Department of Mathematics, K.L.University, Vaddeswaram, Guntur, India.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, first, we investigate the further properties of VLI – ideals on lattice implication algebras. Next, we study the relation between VLI – ideal and vague congruence relation of lattice implication algebras. We show that there is a one - to - one correspondence between the set of all VLI – ideals and the set of all vague congruence relations of lattice implication algebras. We study the homomorphism theorem on lattice implication algebra induced by vague congruence.
Keywords: Lattice implication algebras, VLI – ideals, Vague congruence relation
Cite this paper: T. Anitha, V. Amarendra Babu, Vague Congruence Relation Induced by VLI – Ideals of Lattice Implication Algebras, American Journal of Mathematics and Statistics, Vol. 6 No. 3, 2016, pp. 89-93. doi: 10.5923/j.ajms.20160603.01.
Article Outline
1. Introduction
- In 1993, Y. XU [12] first established the lattice implication algebra by combining lattice and implication algebra. Z. M. Song and Y. Xu [11] studied the congruence relations on lattice implication algebras. Congruence relation is also one of the important tool when an algebra is studied. Lattice implication algebra is a special kind of residuated lattice. Zadeh [14] proposed the theory of fuzzy sets. In1993, W. L. Gau and D.J. Buehrer [5] introduced the concept of vague sets, which are more useful to evaluate the real life problems. The idea of vague sets is that the membership of every element can be classified into two parameters including supporting and opposing. Ranjit Biswas [4] initiated the study of vague algebra by studying vague groups. At first Ya Qin and Yi Liu [9] applied the concept of vague set theory to lattice implication algebras and introduced the notion of v- filter, and investigated some of their properties. Y. Lin et al. [8] studied the fuzzy congruence relations and properties on lattice implication algebras. Kham et al. [7] studied the vague relation and its properties on lattice implication algebras. Ch. Zhong and Y. Qin [15] studied the vague congruence relations and its properties on lattice implication algebras. Xiaoyan Qin et al. [10] studied the vague congruence and quotient lattice implication algebras. There are close correlations among ideals, congruence and quotient algebras. In [1], we introduced the concept of VLI – ideals on lattice implication algebras and studied properties of VLI – ideals.In this paper, we investigate the further properties of VLI – ideals and the relation between VLI – ideals and vague congruence relations.
2. Preliminaries
- Definition 2.1 [12]. Let
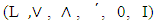 be a complemented lattice with the universal bounds 0, I.
be a complemented lattice with the universal bounds 0, I.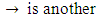 binary operation of L.
binary operation of L. 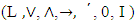 is called a lattice implication algebra, if the following axioms hold,
is called a lattice implication algebra, if the following axioms hold, 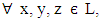
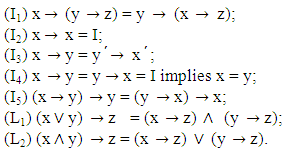 Definition 2.2 [6]. Let A be a subset of a lattice implication algebra L. A is said to be an LI - ideal of L if it satisfies the following conditions:
Definition 2.2 [6]. Let A be a subset of a lattice implication algebra L. A is said to be an LI - ideal of L if it satisfies the following conditions: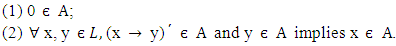 Definition 2.3 [5]. A vague set A in the universal of discourse X is characterized by two membership functions given by:(1) A truth membership function
Definition 2.3 [5]. A vague set A in the universal of discourse X is characterized by two membership functions given by:(1) A truth membership function 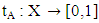 and(2) A false membership function
and(2) A false membership function 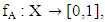 Where tA(x) is a lower bound of the grade of membership of x derived from the “evidence for x”, and fA(x) is a lower bound on the negation of x derived from the “evidence against x” and
Where tA(x) is a lower bound of the grade of membership of x derived from the “evidence for x”, and fA(x) is a lower bound on the negation of x derived from the “evidence against x” and 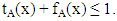 The vague set
The vague set 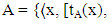
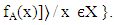 The value of x in the vague set A denoted by
The value of x in the vague set A denoted by 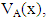 defined by
defined by 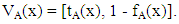 Notation: Let I[0, 1] denote the family of all closed subintervals of [0, 1]. If I1 = [a1, b1], I2 = [a2, b2] are two elements of I[0, 1], we call I1 ≥I2 if a1 ≥a 2 and b1 ≥b2. We define the term imax to mean the maximum of two interval as
Notation: Let I[0, 1] denote the family of all closed subintervals of [0, 1]. If I1 = [a1, b1], I2 = [a2, b2] are two elements of I[0, 1], we call I1 ≥I2 if a1 ≥a 2 and b1 ≥b2. We define the term imax to mean the maximum of two interval as 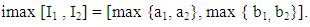 Similarly, we can define the term imin of any two intervals.Definition 2.4 [1]. Let A be a vague set of a lattice implication algebra L. A is said to be a vague LI - ideal of L if it satisfies the following conditions:
Similarly, we can define the term imin of any two intervals.Definition 2.4 [1]. Let A be a vague set of a lattice implication algebra L. A is said to be a vague LI - ideal of L if it satisfies the following conditions: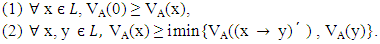 Definition 2.5 [7]. Let X and Y be two universes. A vague relation of the universe X with the universe Y is a vague set of the Cartesian product
Definition 2.5 [7]. Let X and Y be two universes. A vague relation of the universe X with the universe Y is a vague set of the Cartesian product 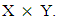 Definition 2.6 [7]. Let X and Y be two universes. A vague subset R of discourse
Definition 2.6 [7]. Let X and Y be two universes. A vague subset R of discourse 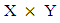 is characterized by two membership functions given by:(1) A truth membership function
is characterized by two membership functions given by:(1) A truth membership function 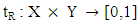 and(2) A false membership function
and(2) A false membership function 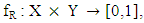 Where tR(x, y) is a lower bound of the grade of membership of (x, y) derived from the “evidence for (x, y)” and fR(x, y) is a lower bound on the negation of (x, y) derived from the “evidence against (x, y)” and tR(x, y) + fR(x, y) ≤ 1.Thus the grade of membership of (x, y) in the vague set R is bounded by subinterval [tR(x, y), 1 – fR(x, y)] of [0,1]. The vague relation R is written as
Where tR(x, y) is a lower bound of the grade of membership of (x, y) derived from the “evidence for (x, y)” and fR(x, y) is a lower bound on the negation of (x, y) derived from the “evidence against (x, y)” and tR(x, y) + fR(x, y) ≤ 1.Thus the grade of membership of (x, y) in the vague set R is bounded by subinterval [tR(x, y), 1 – fR(x, y)] of [0,1]. The vague relation R is written as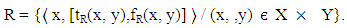 The value of (x, y) in the vague relation R denoted by VR(x, y), defined by
The value of (x, y) in the vague relation R denoted by VR(x, y), defined by 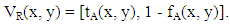 Definition 2.7 [15]. Let X be a nonempty universe. A vague relation R on X is called vague similarity relation, if R satisfies the following conditions:
Definition 2.7 [15]. Let X be a nonempty universe. A vague relation R on X is called vague similarity relation, if R satisfies the following conditions: 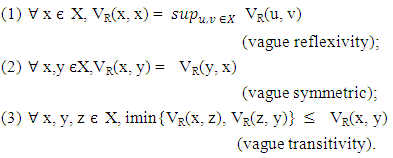 Remark 2.8 [15]. For the vague transitivity,
Remark 2.8 [15]. For the vague transitivity,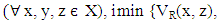
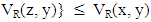
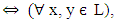
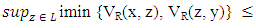
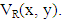 Definition 2.9 [15]. Let R be a vague relation on L. R is said to be a vague congruence relation on L, if
Definition 2.9 [15]. Let R be a vague relation on L. R is said to be a vague congruence relation on L, if 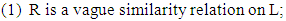
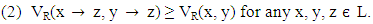 Theorem 2.10 [15]. Let R be a vague relation on L. Then for any
Theorem 2.10 [15]. Let R be a vague relation on L. Then for any 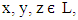 R satisfies the following conditions:
R satisfies the following conditions: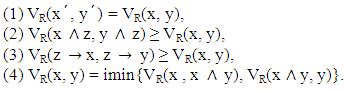
3. Some Properties of VLI – ideals
- Theorem 3.1: The vague set A of L is a VLI – ideal if and only if A satisfies the following conditions:
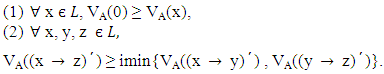 Proof: suppose A is a VLI – ideal of L. Obviously A satisfies the first condition.
Proof: suppose A is a VLI – ideal of L. Obviously A satisfies the first condition.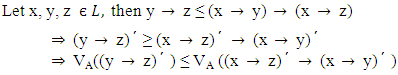 It follows that,
It follows that, 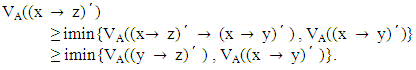 Conversely suppose that the vague set A of L satisfies the inequalities (1) and (2).Taking z = 0 in (2), we get
Conversely suppose that the vague set A of L satisfies the inequalities (1) and (2).Taking z = 0 in (2), we get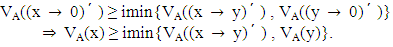 Hence A is a VLI – ideal of L.Theorem 3.2: The vague set A of L is a VLI – ideal of L if and only if for any
Hence A is a VLI – ideal of L.Theorem 3.2: The vague set A of L is a VLI – ideal of L if and only if for any 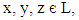
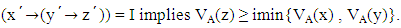 Proof: Suppose A is a VLI – ideal of L.
Proof: Suppose A is a VLI – ideal of L.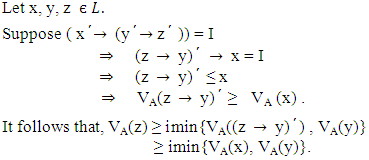 Conversely suppose that the vague set A of L satisfies the condition
Conversely suppose that the vague set A of L satisfies the condition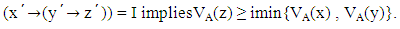 Then, we have
Then, we have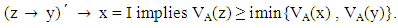 Let
Let 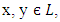 then
then 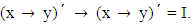 It follows that
It follows that 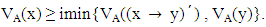 So A is a VLI – ideal of L.Corrolary 3.3: The vague set A of L is a VLI – ideal of L if and only if A satisfies the condition
So A is a VLI – ideal of L.Corrolary 3.3: The vague set A of L is a VLI – ideal of L if and only if A satisfies the condition 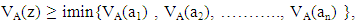 where
where 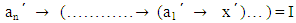 for a1, a2, ……….., an є L.Definition 3.4: Let A be a VLI – ideal of L. Then for any
for a1, a2, ……….., an є L.Definition 3.4: Let A be a VLI – ideal of L. Then for any 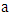
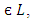 the set A[a] defined by
the set A[a] defined by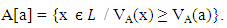 Theorem 3.5: Let A be a VLI – ideal of L. Then A[a] is an ideal of L.Proof: Let A be a VLI – ideal of L.
Theorem 3.5: Let A be a VLI – ideal of L. Then A[a] is an ideal of L.Proof: Let A be a VLI – ideal of L. 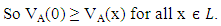 Obviously
Obviously 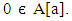 Let
Let 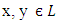 such that
such that 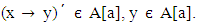
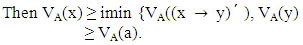
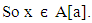 Therefore A[a] is an ideal of L.Theorem 3.6: Let A be a vague set of L and A[a] be an ideal of L for any
Therefore A[a] is an ideal of L.Theorem 3.6: Let A be a vague set of L and A[a] be an ideal of L for any 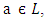 then
then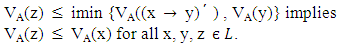 Proof: Let A[a] be an ideal of L for any
Proof: Let A[a] be an ideal of L for any 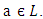 Let
Let 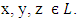
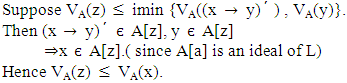 Theorem 3.7: Let A be a vague set of L and A satisfies
Theorem 3.7: Let A be a vague set of L and A satisfies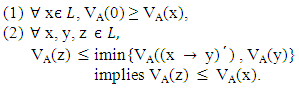 Then A[a] is an ideal of L for any
Then A[a] is an ideal of L for any 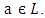 Proof: Let A be a vague set of L and A satisfies the above conditions.
Proof: Let A be a vague set of L and A satisfies the above conditions.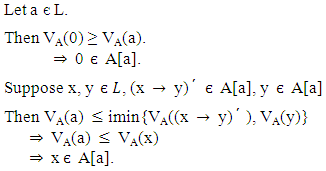 Therefore A[a] is an ideal of L.
Therefore A[a] is an ideal of L.4. Vague Congruence Relation Induced by VLI – ideals
- Theorem 4.1: Let R be a vague congruence relation on L. Then, for all x, y, z є L,
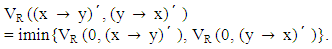
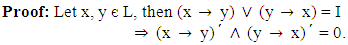 Since R is a vague congruence relation,
Since R is a vague congruence relation,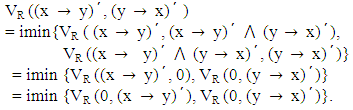 Theorem 4.2: Let R be a vague congruence relation on L. Then the vague set
Theorem 4.2: Let R be a vague congruence relation on L. Then the vague set 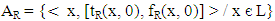 is a VLI – ideal of L.Proof: (1) Let x є L, then
is a VLI – ideal of L.Proof: (1) Let x є L, then 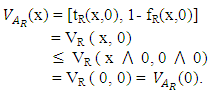 Therefore
Therefore 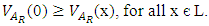 (2) Let
(2) Let 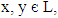 then
then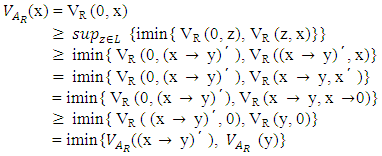 Therefore AR is a vague LI – ideal of L. AR is called a vague LI – ideal induced by a vague congruence relation R.Definition 4.3: Let R be a similarity relation on L. For each a є L, we define a vague subset
Therefore AR is a vague LI – ideal of L. AR is called a vague LI – ideal induced by a vague congruence relation R.Definition 4.3: Let R be a similarity relation on L. For each a є L, we define a vague subset 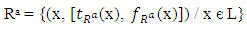 on L, where
on L, where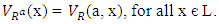 Theorem 4.4: Let R be a vague congruence relation on L. Then, R0 is vague LI – ideal of L. Proof: It is obvious from the theorem 4.2.Theorem 4.5: Let A be a vague LI – ideal of L and RA be a vague relation on L defined by
Theorem 4.4: Let R be a vague congruence relation on L. Then, R0 is vague LI – ideal of L. Proof: It is obvious from the theorem 4.2.Theorem 4.5: Let A be a vague LI – ideal of L and RA be a vague relation on L defined by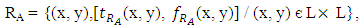 Where
Where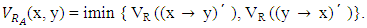 Then RA is a vague congruence relation on L.Proof: Let RA be a vague relation on L defined by
Then RA is a vague congruence relation on L.Proof: Let RA be a vague relation on L defined by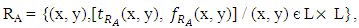 Where
Where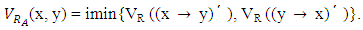 It is clear RA is reflexive and symmetric. For any
It is clear RA is reflexive and symmetric. For any 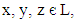 we have
we have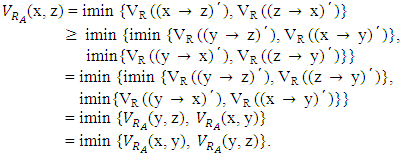 Therefore RA is transitive.
Therefore RA is transitive.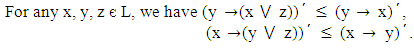 Since A is order reversing, we have
Since A is order reversing, we have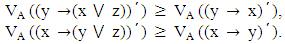 It follows that,
It follows that,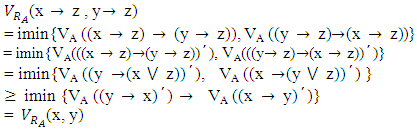 Therefore RA is a vague congruence relation on L. RA is called a vague congruence relation induced by a vague LI – ideal A of L.Theorem 4.6: Let the set of all vague LI – ideals of L denoted by IV(L) and the set of all vague congruence relations of L denoted by CV(L). Then IV(L) is isomorphic to CV(L).Proof: We define the mappings f and g as follows:
Therefore RA is a vague congruence relation on L. RA is called a vague congruence relation induced by a vague LI – ideal A of L.Theorem 4.6: Let the set of all vague LI – ideals of L denoted by IV(L) and the set of all vague congruence relations of L denoted by CV(L). Then IV(L) is isomorphic to CV(L).Proof: We define the mappings f and g as follows: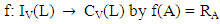 and
and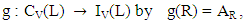 for any
for any 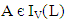 and
and 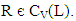 Obviously these mappings are well defined. For any
Obviously these mappings are well defined. For any 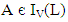 and
and 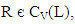
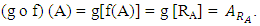 For any
For any 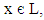 we have
we have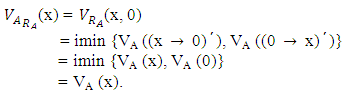
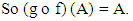 That is (g o f) is an identical mapping on IV(L), which implies that f is injective.Let
That is (g o f) is an identical mapping on IV(L), which implies that f is injective.Let 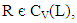 then AR is a vague LI – ideal of L.Then
then AR is a vague LI – ideal of L.Then 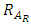 is a congruence relation on L.For any
is a congruence relation on L.For any 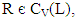
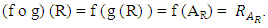 For any
For any 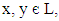 we have
we have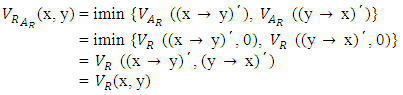 That implies (f o g) (R) = R. That is f o g is an identical mapping on CV(L) which implies that f is surjective.So f is a bijection from IV(L) to CV(L). Therefore IV(L) is isomorphic to CV(L).Theorem 4.7: Let A be a vague LI – ideal of L and RA be a vague congruence relation induced by A. Then for any
That implies (f o g) (R) = R. That is f o g is an identical mapping on CV(L) which implies that f is surjective.So f is a bijection from IV(L) to CV(L). Therefore IV(L) is isomorphic to CV(L).Theorem 4.7: Let A be a vague LI – ideal of L and RA be a vague congruence relation induced by A. Then for any 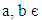
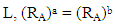 if and only if
if and only if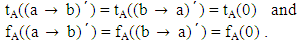 Proof: Let
Proof: Let 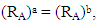 we have
we have 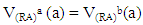 for all
for all 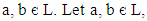 then
then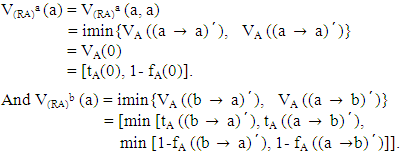 It follows that,
It follows that, 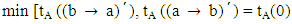 and
and 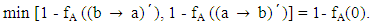
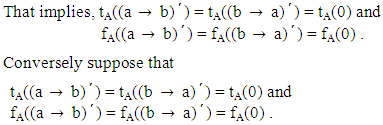
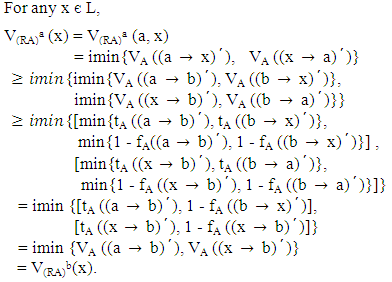 Similarly, we can prove that
Similarly, we can prove that 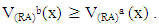 Therefore
Therefore 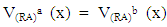 for all
for all  hence
hence 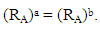 Theorem 4.8: Let A be a VLI – ideal of L. Define
Theorem 4.8: Let A be a VLI – ideal of L. Define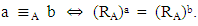 Then,
Then, 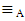 is a congruence relation on L.Proof: The proof can be obtained from theorem 4.7.Theorem 4.9: Let A be a VLI – ideal of L and let L/ RA be the corresponding quotient algebra. Then, the map
is a congruence relation on L.Proof: The proof can be obtained from theorem 4.7.Theorem 4.9: Let A be a VLI – ideal of L and let L/ RA be the corresponding quotient algebra. Then, the map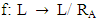 defined by
defined by  for any
for any  is a lattice implication homomorphism and
is a lattice implication homomorphism and 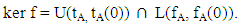 Proof: Since A is a VLI – ideal of L, RA is a vague congruence relation induced by A. By proposition 24 (10),
Proof: Since A is a VLI – ideal of L, RA is a vague congruence relation induced by A. By proposition 24 (10),  is a lattice implication homomorphism.
is a lattice implication homomorphism.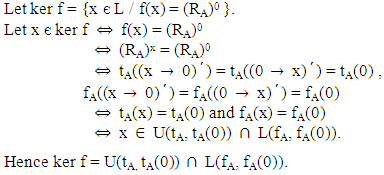
5. Conclusions
- Congruence theory and ideal theory play very important role in research of logic algebra. Through which we can much information such as quotient structure and homomorphic image of the logic algebra. The aim of this paper is to develop the vague congruence relation induced by VLI – ideals on lattice implication algebras. We study the concept of vague congruence induced by VLI – ideals. First, some properties of VLI – ideals are investigated. Next, some properties of vague congruence relation induced by VLI – ideals are discussed. We obtain one - to - one correspondence between the set of all VLI – ideals and the set of all vague congruence relations of lattice implication algebras. Lastly we obtain the homomorphism theorem on lattice implication algebra induced by vague congruence. We hope that it will be of great use to provide theoretical foundation to design for enriching corresponding many – valued logical system.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML