Amnah E. Shammaky
Department of Mathematics, Faculty of Science, Jazan University, Jazan, Saudi Arabia
Correspondence to: Amnah E. Shammaky , Department of Mathematics, Faculty of Science, Jazan University, Jazan, Saudi Arabia.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this paper, we investigate the majorization problem of certain classes of meromorphic multivalent functions defined by differential operator.
Keywords:
Meromorphic, Multivalent functions, Majorization problem, Complex order and differential operator
Cite this paper: Amnah E. Shammaky , Majorization Problem for Certain Classes of Meromorphic Multivalent Functions Defined by Differential Operator, American Journal of Mathematics and Statistics, Vol. 6 No. 2, 2016, pp. 86-88. doi: 10.5923/j.ajms.20160602.03.
1. Introduction
If 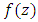 and
and 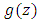 are analytic in
are analytic in 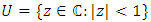 we say that
we say that 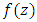 subordinate to
subordinate to 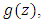 written
written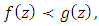 | (1) |
if there exist a Schwarz function 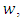 which is analytic in
which is analytic in 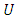 with
with 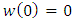 and
and 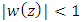 for all
for all 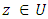 such that
such that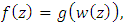 | (2) |
Furthermore, if the function 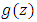 is univalent in
is univalent in 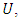 then we have the following equivalence (see [7]):
then we have the following equivalence (see [7]):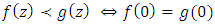 and
and 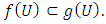 The pioneering work of [9], we say that
The pioneering work of [9], we say that 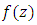 is majorized by
is majorized by 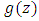 in
in 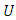 and write
and write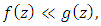 | (3) |
If there exists a function 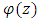 analytic in
analytic in 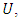 such that
such that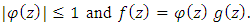 Let
Let 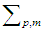 denote the class of function
denote the class of function 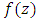 of the form
of the form 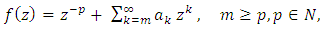 | (4) |
which are analytic and multivalent in the punctured unit disc 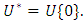 For
For 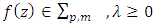 and
and 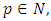 we have (see [10])
we have (see [10])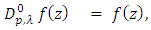
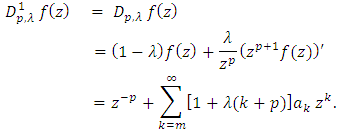 In general, we have
In general, we have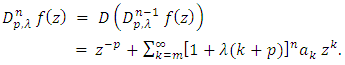 | (5) |
Note that for 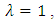 we have the operator
we have the operator 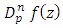 studied by Aouf and Hossen [5], Aouf and Al-Ashwah [4], Liu and Srivastava [8] and Srivastava and patel [13]. Also when
studied by Aouf and Hossen [5], Aouf and Al-Ashwah [4], Liu and Srivastava [8] and Srivastava and patel [13]. Also when 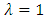 and
and 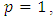 we have the operator
we have the operator 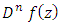 studied by Urafegaddi and Somaatha [14].The following relation for the operator
studied by Urafegaddi and Somaatha [14].The following relation for the operator 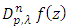 can be obtained by Simple Calculation (see [10])
can be obtained by Simple Calculation (see [10]) 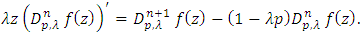 | (6) |
By making use of the operator 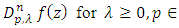
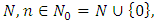 we define the following class.Let
we define the following class.Let 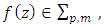 then
then 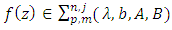 if and only if
if and only if 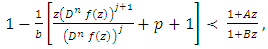 | (7) |
where 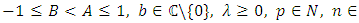
 The majorization (3) is closely related to the concept of quasi-subordination between analytic functions in
The majorization (3) is closely related to the concept of quasi-subordination between analytic functions in 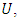 which was considered by Altinatas and Owa [2]. Recently, Ali [1] results investigated some majorization results for some classes of meromorphic multivalent functions defined by integral operator.In the present paper, as a sequel to the work of [1] and [6], we investigate majorization problem for the class
which was considered by Altinatas and Owa [2]. Recently, Ali [1] results investigated some majorization results for some classes of meromorphic multivalent functions defined by integral operator.In the present paper, as a sequel to the work of [1] and [6], we investigate majorization problem for the class 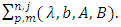
2. Majorization Problem for the Class ∑p,m
We shall assume throughout the paper that where 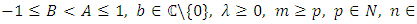
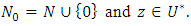 Theorem 2.1. Let the function
Theorem 2.1. Let the function 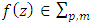 and suppose that
and suppose that 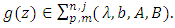 If
If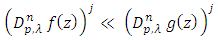 in
in 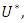 then
then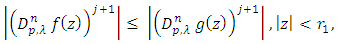 where
where 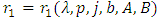 is the smallest positive root of the equation
is the smallest positive root of the equation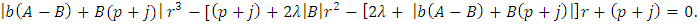 | (8) |
Proof. Since 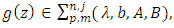 from (7), we get
from (7), we get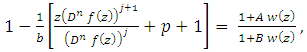 | (9) |
where 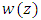 is analytic function in
is analytic function in  with
with 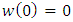 and
and 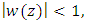 then we have
then we have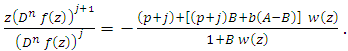 | (10) |
Since 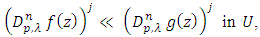 therefore
therefore 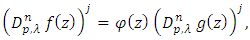 | (11) |
where 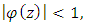 differentiating it with respect to
differentiating it with respect to 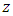 and multiplying by
and multiplying by 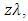 we get
we get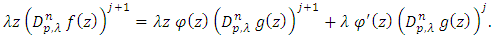 | (12) |
Thus, by noting that 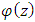 satisfies the inequality (see [1])
satisfies the inequality (see [1])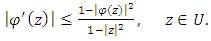 | (13) |
Using equations (11) and (12) and inequality (13), we obtain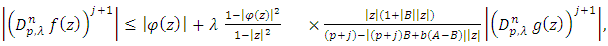 | (14) |
which upon setting 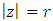 and
and 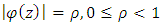 in (14) leads to the inequality
in (14) leads to the inequality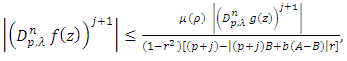 | (15) |
where 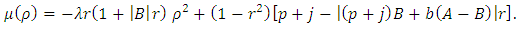 | (16) |
Takes its maximum value at 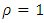 with
with 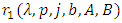 is the smallest positive root of (8). Therefore, the function
is the smallest positive root of (8). Therefore, the function 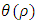 defined by
defined by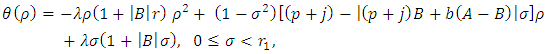 | (17) |
is an increasing function for 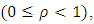 so that
so that where
where 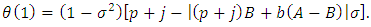 Hence, upon setting
Hence, upon setting 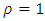 in (17), we conclude that (8) holds true for
in (17), we conclude that (8) holds true for 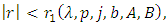 which complete the proof.Putting
which complete the proof.Putting 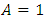 and
and 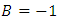 in Theorem 2.1, we obtain the following corollary: Corollary 2.2. Let the function
in Theorem 2.1, we obtain the following corollary: Corollary 2.2. Let the function 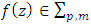 and suppose that
and suppose that 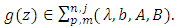 If
If 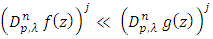 in
in 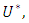 then
then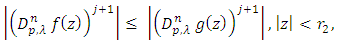 where
where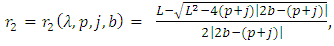 | (18) |
and 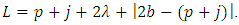 Putting
Putting 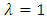 in corollary 2.2, we obtain the following corollary:Corollary 2.3. Let the function
in corollary 2.2, we obtain the following corollary:Corollary 2.3. Let the function 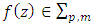 and suppose that
and suppose that 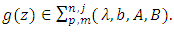 If
If 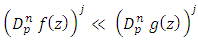 in
in 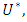 then
then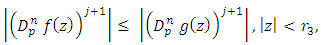 Where
Where 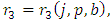 given by (18) with
given by (18) with 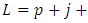
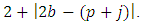 Putting
Putting 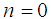 in corollary 2.3, we obtain the following corollary: Corollary 2.4. Let the function
in corollary 2.3, we obtain the following corollary: Corollary 2.4. Let the function 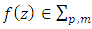 and suppose that
and suppose that 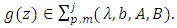 If
If 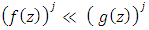 in
in 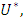 then
then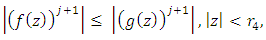 Where
Where 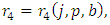 given by (18) with
given by (18) with 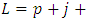
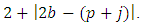 Remark 2.5. Putting
Remark 2.5. Putting 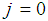 in corollary 2.4, we obtain the result of Ali ([1], Corollary 3).
in corollary 2.4, we obtain the result of Ali ([1], Corollary 3).
ACKNOWLEDGEMENTS
The author would like to thank the referee(s) for his/her helpful comments.
References
| [1] | Ali E.E., 2013, Majorization properties for certain classes of meromorphic p-valent functions defined by integral operator, J.F.C. and Appl. 4(3S) N.5, 1-6. [http://www.facj.webs.com/]. |
| [2] | Altintas O. and Owa S., 1992, Majorization and quassi-subordination for certain analytic functions, Proc. Japan. Acad. SerA.Math.Sci 68, 181-185. |
| [3] | Aouf M.K., 1993, New criterion for multivalent meromorphic starlike function of Alpha, Proc.Japon Acad.SerA.Math.sci 69, 66-70. |
| [4] | Aouf M.K. and El-Ashwah R.M., 2009, Subclasses of meromorphically p-valent functions with negative coefficients associated with a linear operator, Bull. Instiute Math., 4, N.1, 97-118. |
| [5] | Aouf M.K and Hossen H.M., 1993, New criteria for meromorphic p-valent starlike functions, Tsukuba J. Math., 17, 481-486. |
| [6] | Dhuria K. and Mathur R., 2013, Majorization for certain classes of meromorphic functions defined by integral operator, Int. J. Open Problems Complex Analysis 5, N.3, 50-56. [http://www.i-csrs.org]. |
| [7] | Goodman A.W.: Univalent Functions, Vol. I, Mariner Publishing Company, Tamps, Florida. 1983. |
| [8] | Liu J.L. and Srivastava H.M., 2004, Subclasses of meromorphic multivalent functions associated with acertain linear operator, Math, compd. Modeling, 39, 35-44. [http://www.Science direct.com]/Science/article/pii/S089571770490543. “PDCA12-70 data sheet,” Opto Speed SA, Mezzovico, Switzerland. |
| [9] | Macgregor T.H., 1967, Majorization by univalent functions, Duke Math. J., 34, 95-102. |
| [10] | Mohammed A. and Darus M., 2014, On new p-valent meromrphic function involving certain differential and integral operator, Abstract and Applied Analysis 2014, Article ID208530, 7pages.[http:dx.doi.org/10.1155/2014/208530]. |
| [11] | Owa S., Nunokawa M. and Saitoh H., 1989, Generalization of certain subclasses of meromorphic univalent functions, J.Fac.Sci, Tach. Kinki. Univ., 25, 21-27. |
| [12] | Pommerenke C., 1963, On meromorphic starlike functions, Pacific J. Math. 13, 221-235. |
| [13] | Srivastava H.M. and Patel J., 2005, Applications of differential snbordination to certain subclasses of meromorphicalty multivalent functions, J.Ineq. Pure and Appl. Math., 6, N. 3, Art 88.[http://jipam.vu.edu.au/article.php?sid=561]. |
| [14] | Uralegaddi B.A. and Somanatha C., 1991, New critera for meromorphic starlike univalent functions, Bull. Austral. Math. Sci. 43, 137-140. |


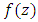 and
and 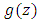 are analytic in
are analytic in 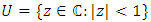 we say that
we say that 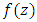 subordinate to
subordinate to 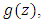 written
written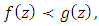
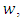 which is analytic in
which is analytic in 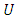 with
with 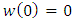 and
and 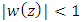 for all
for all 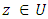 such that
such that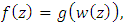
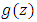 is univalent in
is univalent in 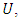 then we have the following equivalence (see [7]):
then we have the following equivalence (see [7]):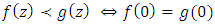 and
and 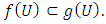 The pioneering work of [9], we say that
The pioneering work of [9], we say that 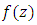 is majorized by
is majorized by 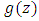 in
in 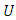 and write
and write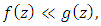
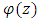 analytic in
analytic in 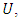 such that
such that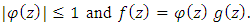 Let
Let 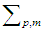 denote the class of function
denote the class of function 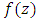 of the form
of the form 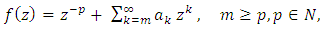
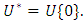 For
For 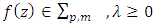 and
and 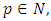 we have (see [10])
we have (see [10])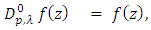
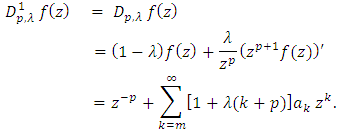 In general, we have
In general, we have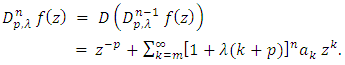
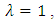 we have the operator
we have the operator 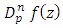 studied by Aouf and Hossen [5], Aouf and Al-Ashwah [4], Liu and Srivastava [8] and Srivastava and patel [13]. Also when
studied by Aouf and Hossen [5], Aouf and Al-Ashwah [4], Liu and Srivastava [8] and Srivastava and patel [13]. Also when 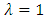 and
and 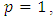 we have the operator
we have the operator 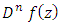 studied by Urafegaddi and Somaatha [14].The following relation for the operator
studied by Urafegaddi and Somaatha [14].The following relation for the operator 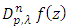 can be obtained by Simple Calculation (see [10])
can be obtained by Simple Calculation (see [10]) 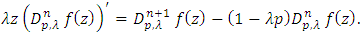
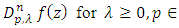
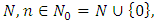 we define the following class.Let
we define the following class.Let 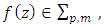 then
then 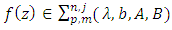 if and only if
if and only if 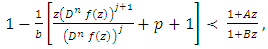
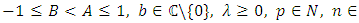
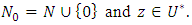
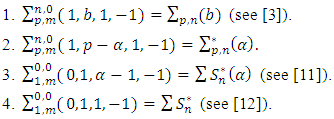 The majorization (3) is closely related to the concept of quasi-subordination between analytic functions in
The majorization (3) is closely related to the concept of quasi-subordination between analytic functions in 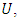 which was considered by Altinatas and Owa [2]. Recently, Ali [1] results investigated some majorization results for some classes of meromorphic multivalent functions defined by integral operator.In the present paper, as a sequel to the work of [1] and [6], we investigate majorization problem for the class
which was considered by Altinatas and Owa [2]. Recently, Ali [1] results investigated some majorization results for some classes of meromorphic multivalent functions defined by integral operator.In the present paper, as a sequel to the work of [1] and [6], we investigate majorization problem for the class 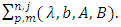
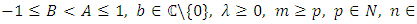
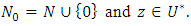 Theorem 2.1. Let the function
Theorem 2.1. Let the function 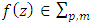 and suppose that
and suppose that 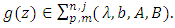 If
If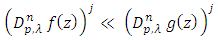 in
in 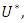 then
then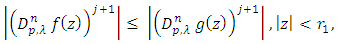 where
where 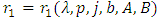 is the smallest positive root of the equation
is the smallest positive root of the equation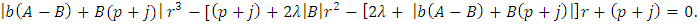
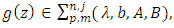 from (7), we get
from (7), we get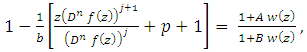
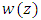 is analytic function in
is analytic function in 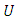 with
with 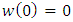 and
and 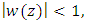 then we have
then we have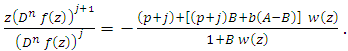
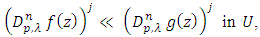 therefore
therefore 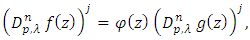
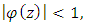 differentiating it with respect to
differentiating it with respect to 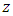 and multiplying by
and multiplying by 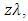 we get
we get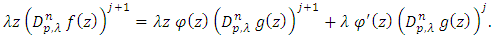
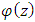 satisfies the inequality (see [1])
satisfies the inequality (see [1])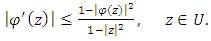
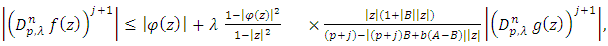
 and
and  in (14) leads to the inequality
in (14) leads to the inequality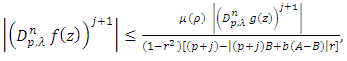
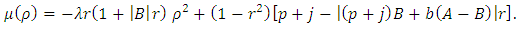
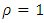 with
with 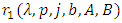 is the smallest positive root of (8). Therefore, the function
is the smallest positive root of (8). Therefore, the function 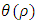 defined by
defined by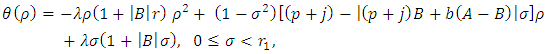
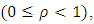 so that
so that where
where 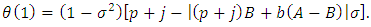 Hence, upon setting
Hence, upon setting 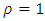 in (17), we conclude that (8) holds true for
in (17), we conclude that (8) holds true for 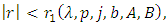 which complete the proof.Putting
which complete the proof.Putting 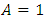 and
and 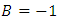 in Theorem 2.1, we obtain the following corollary: Corollary 2.2. Let the function
in Theorem 2.1, we obtain the following corollary: Corollary 2.2. Let the function 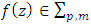 and suppose that
and suppose that 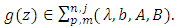 If
If 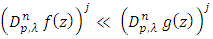 in
in 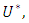 then
then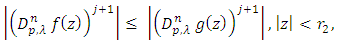 where
where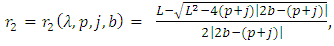
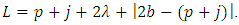 Putting
Putting 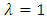 in corollary 2.2, we obtain the following corollary:Corollary 2.3. Let the function
in corollary 2.2, we obtain the following corollary:Corollary 2.3. Let the function 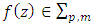 and suppose that
and suppose that 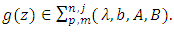 If
If 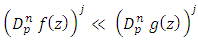 in
in 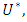 then
then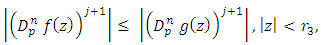 Where
Where 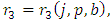 given by (18) with
given by (18) with 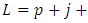
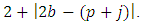 Putting
Putting 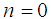 in corollary 2.3, we obtain the following corollary: Corollary 2.4. Let the function
in corollary 2.3, we obtain the following corollary: Corollary 2.4. Let the function 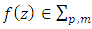 and suppose that
and suppose that 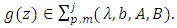 If
If 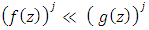 in
in 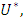 then
then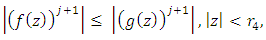 Where
Where 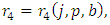 given by (18) with
given by (18) with 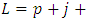
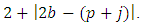 Remark 2.5. Putting
Remark 2.5. Putting 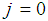 in corollary 2.4, we obtain the result of Ali ([1], Corollary 3).
in corollary 2.4, we obtain the result of Ali ([1], Corollary 3).  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML