Oyeka I. C. A., Umeh E. U.
Department of Statistics, Nnamdi Azikiwe University, Awka, Nigeria
Correspondence to: Umeh E. U., Department of Statistics, Nnamdi Azikiwe University, Awka, Nigeria.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper proposes and presents a statistical method for the estimation of joint, marginal and conditional odds that a randomly selected susceptible in a population is infected with some diseases and the numbers of subjects infected assuming that no prior interventionist actions have been taken to influence disease outcomes. The proposed method is intended to help guide health officials make informed decisions on the use of medical resources in the presence of scarcity. Although, it is possible to hypothesis and fit some theoretical probability distribution models to data on disease prevalence rates, and use them in estimating desired odds of infection. The proposed method is however less tedious to apply in practice and the results obtained are relatively easier to interpret and explain. The method is illustrated with some data.
Keywords:
Variables, Disease Infections, Joint, Marginal and Conditional Odds, Probability Estimation, Models
Cite this paper: Oyeka I. C. A., Umeh E. U., A Three Variable Disease Infection Probability Estimation Model, American Journal of Mathematics and Statistics, Vol. 6 No. 1, 2016, pp. 36-43. doi: 10.5923/j.ajms.20160601.04.
1. Introduction
At any given point in time there may be many types of diseases existing in a population. A public health worker may in this situation wish to estimate the odds and sizes of the population likely to be infected by either individual diseases or clusters of these diseases assuming that the diseases follow their natural course of occurrence in the population without any prior interventionist remedial actions to guide their management [3-8].In this paper, we propose a statistical method for estimating the odds that a randomly selected individual or subject from a population of interest is infected by an existing disease and the likely number of subjects in the population so infected, assuming the infections follow the natural course without medical interventions. The method also enables one estimate joint and conditional probabilities that randomly selected subjects or patients are infected and not infected by all or some diseases from three family types of diseases either simultaneously or infected and not infected by some diseases before or after some other diseases operating as predisposing or antecedent diseases in a population. This would enable policy makers and further research either to prove or disprove existing theories and methods. This approach clearly keeps research in a state of continuous flukes and advances knowledge and academics. This is the hope for approach of this present paper.
2. The Proposed Method
Suppose there are several diseases existing in a certain population. Although the proposed method may be used with the diseases treated as individual events, we will here for simplicity but without loss of generality assume that the diseases could be grouped into a finite number of clusters of diseases where the clusters are intra-homogeneous among and inter-heterogeneous between themselves. For example, the diseases may be grouped into cardio-vascular diseases, infectious diseases, congenital diseases, auto immune and nutritional disorder diseases, mental disorder and others. These clusters may be denoted with A, B, C etc. In particular, we will in this paper assume that research interest is in only three existing conditions, diseases, clusters or groups of diseases A, B, and C, for instance greatest epidemiological concern infecting subjects in a given population and also interest is in estimating the joint, marginal and conditional probabilities that a randomly selected subject from the population is infected or not infected with the diseases and the number of subjects so affected to help guide management decisions in the presence of limited medical resources [9-15]. Now a randomly selected individual or subject from this population of current susceptible population size N may suffer from none, one, some combinations of, or all of the diseases in groups A, B and C.Let A, B and C be the possibility that a randomly selected subject or individual may be infected with disease A, B and C respectively. Let 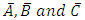 be the possibility that a randomly selected subject or individual may not be infected with disease A, B and C respectively. Let ABC be the possibility that a randomly selected subject from the population is infected by all the diseases in the three disease groups. Let
be the possibility that a randomly selected subject or individual may not be infected with disease A, B and C respectively. Let ABC be the possibility that a randomly selected subject from the population is infected by all the diseases in the three disease groups. Let 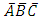 be the possibility that a randomly selected subject from the population is not infected with any of the three diseases. Let
be the possibility that a randomly selected subject from the population is not infected with any of the three diseases. Let 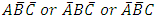 be the possibility that a randomly selected subject from the population is infected with only one of the three diseases. Let also
be the possibility that a randomly selected subject from the population is infected with only one of the three diseases. Let also 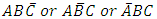 be the possibility that a randomly selected subject from the population is infected by only two of the three diseases.Hence possible configurations of the occurrence of these diseases in a subject and in the population may be presented as in Table 1.
be the possibility that a randomly selected subject from the population is infected by only two of the three diseases.Hence possible configurations of the occurrence of these diseases in a subject and in the population may be presented as in Table 1.Table 1. Possible Configurations of Diseases in a Population
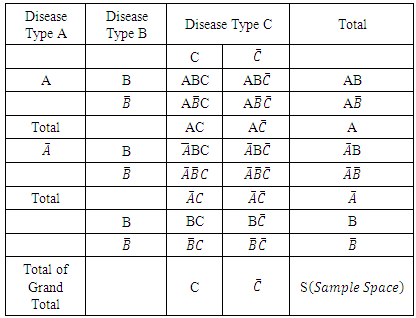 |
| |
|
Of course there are many other possible configurations of the occurrence or non occurrence of these diseases in a population. For example, a randomly selected subject or individual may or may not be infected with disease B say given that he is already infected or not infected with disease A say; the subject may or may not be infected with diseases B and C, say given that he is already infected or not infected with disease A say; the subject may or may not be infected with disease A say, given that he is already infected or not infected with diseases B and C say; the subject may have been infected or not infected with disease B say given that he is free of disease A and not of disease C say; etc.Research interest may then be in estimating the probabilities of all three and similar events and the number of persons in the population expected to be so infected, if all things are equal. It is quite possible to hypothesize and fit some theoretical probability distributions such as the Gamma family or other families of distributions to the prevalence values or rates of the diseases or families of diseases of interest and use them to estimate any desired probabilities and the numbers of subjects so affected [1, 2]. This approach would however be rather tedious to use and the estimates so obtained difficult to interpret in practical applications. We will therefore adopt an alternative relatively simpler approach to the problem.Now suppose that the prevalence rates or the probabilities of the occurrence of events A, B, and C in the population are known, that is suppose that the probabilities that a randomly selected subject from the population is infected with or suffers from any of the diseases in disease groups A, B, and C are known to be ‘a’, ‘b’ and ‘c’ respectively. Furthermore, suppose that it is also known that the relationship between the clusters of diseases and that P(B/A) = d; P(C/A) = e; P(C/B) = f; and P(C/AB) = g for diseases in disease groups A, B and C. With this information, we may also easily calculate other similar conditional and joint probabilities. For example, the conditional probability that a randomly selected subject from the population is infected with disease A given that the subject already has disease B is 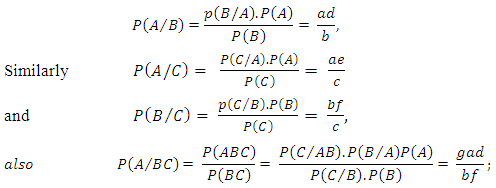
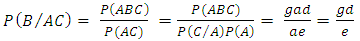 | (1) |
However of greater research interest may be in estimating the probabilities of the joint occurrence or non occurrence of all or some combinations of the three disease entities A, B and C in a population.Now using these known probability values further, we then have that the probability that a randomly selected subject from the population is infected by all the disease in the three disease groups is 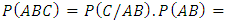
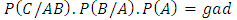 .The probability that a randomly selected subject from the population is not infected with any of the three diseases, that is in disease condition
.The probability that a randomly selected subject from the population is not infected with any of the three diseases, that is in disease condition 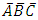 is
is 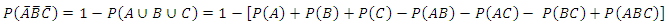 | (2) |
which when evaluated gives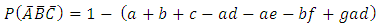 | (3) |
Other joint probabilities in Table 1 are similarly estimated and the results are presented in Table 2 below Now the probability that a randomly selected subject is infected with only one of the three diseases; that is disease condition 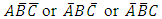 is from Table 2
is from Table 2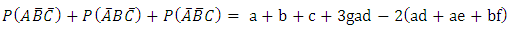 | (4) |
Table 2. Estimated probabilities of occurrence for the joint events in Table 1
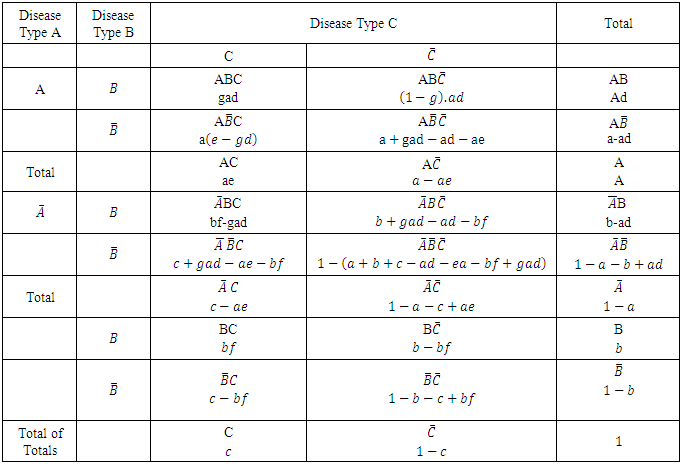 |
| |
|
Note however that Equation 4 is also easily shown to reduce to
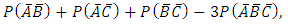 where
where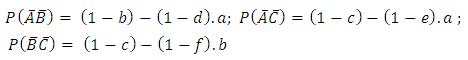 | (5) |
and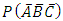 is given in Equation 3.The probability that a randomly selected subject from the population is affected by only two of the three diseases; that is the probability of the events
is given in Equation 3.The probability that a randomly selected subject from the population is affected by only two of the three diseases; that is the probability of the events 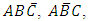 and
and  may be similarly obtained as the sum of the values of the probabilities of these events in Table 2 as
may be similarly obtained as the sum of the values of the probabilities of these events in Table 2 as 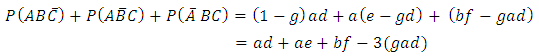 | (6) |
Furthermore, the conditional probability that a randomly selected subject from the population is infected by disease A say, given that the subject has been treated or has natural or acquired immunity against disease entities B and C say is the probability of the event 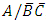 , that is
, that is 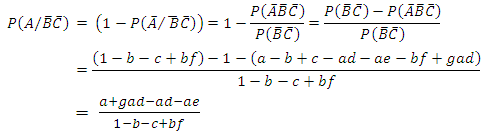 | (7) |
Hence the conditional probability that a randomly selected subject from the population is infected by any one of the three disease entities or groups given that the subject has been treated or has immunity against the other two disease groups is obtained as the probability of the events 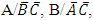 and
and 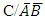 which is calculated as
which is calculated as 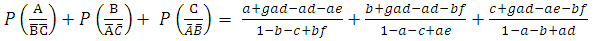 | (8) |
The probability that a randomly selected subject is infected by any two of the family of diseases B and C say given that the subject has been cured or has immunity against the other family of disease A say is the probability of the event 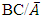 which is estimated as
which is estimated as 
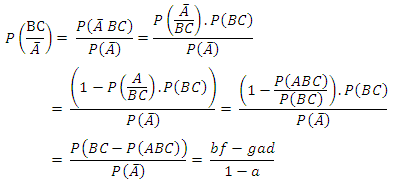 Hence the probability that a randomly selected subject is infected by any two of the family of diseases given that the subject has been cured or has immunity against the other family of diseases is the probability of the events
Hence the probability that a randomly selected subject is infected by any two of the family of diseases given that the subject has been cured or has immunity against the other family of diseases is the probability of the events 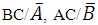 and ,
and , 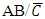 which is estimated as the probability
which is estimated as the probability 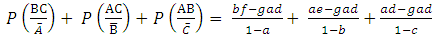 | (9) |
The probability that a randomly selected subject from the population is currently infected with disease C say given that the subject is known to be free from disease A but not free from disease B say is the probability of the event 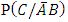 which is given as
which is given as 
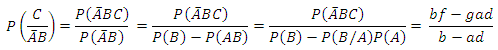 Hence the probability that a randomly selected subject from the population is currently infected with one of the diseases in three families of diseases given that the subject had earlier been infected with diseases in one of the remaining families is the probability of the events
Hence the probability that a randomly selected subject from the population is currently infected with one of the diseases in three families of diseases given that the subject had earlier been infected with diseases in one of the remaining families is the probability of the events 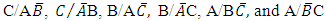 which is calculated as
which is calculated as 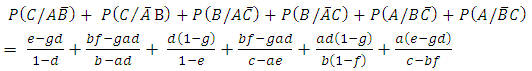 | (10) |
The probability that a randomly selected subject from the population is currently not infected with diseases in any one of the three families of diseases given that the subject had earlier been infected with diseases in one of the two remaining disease families is of course the complement of the estimated probability given in Equation 10. Also the probability that a randomly selected subject from the population who is known to have in the recent past not been affected with A and B say of the three families of the diseases is currently not free from infection with the remaining one C say is the probability of the event 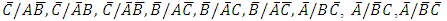 The probability is easily obtained using the estimates in Table 2 and Equation 5 as
The probability is easily obtained using the estimates in Table 2 and Equation 5 as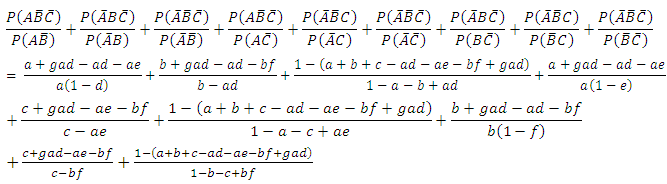 | (11) |
The probability that a randomly selected subject who is already infected by any two of the diseases is currently free from infection with the third disease is the probability of the events 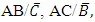 and
and 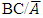 which is given as
which is given as 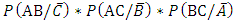 or equivalently using the result of Table 2
or equivalently using the result of Table 2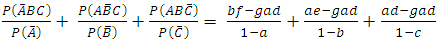 | (12) |
Similarly the probability that a randomly selected subject who is known to be free from infection with any two of the three diseases is currently infected with only one of them is obtained as 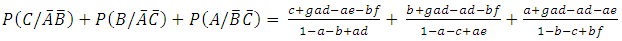 | (13) |
Also the probability that a randomly selected subject from the population who is known to have in the recent past been infected with any two say A and B of the three families of the diseases is currently free from infection with the remaining one C say is the probability of the event 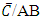 which is calculated using the value in Table 2 as
which is calculated using the value in Table 2 as | (14) |
A researcher may of course be interested in estimating the odds of infection with only two of the three diseases identified in a population. For example, interest may be in estimating the probabilities that a randomly selected subject from the population is infected or not infected simultaneously with diseases A and B say; the probabilities that the subject is infected with one of the two diseases A and not with the other B say or vice versa or the probabilities that a subject who is known not to have been infected with disease B is currently infected with disease A or the probability that the subject who is known not to have been infected with disease B is currently also free from infection with disease A, say; etc. These are the probabilities of the events AB, 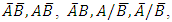 etc. The probabilities can easily be obtained from Table 2 as the sum of the joint probabilities of occurrence or non occurrence of events or diseases A and B summed over events C and
etc. The probabilities can easily be obtained from Table 2 as the sum of the joint probabilities of occurrence or non occurrence of events or diseases A and B summed over events C and  , that is the marginal probabilities of occurrence or non occurrence of the compound event AB, say. Thus
, that is the marginal probabilities of occurrence or non occurrence of the compound event AB, say. Thus 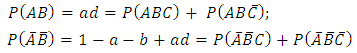 | (15) |
similarly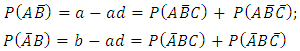 | (16) |
The conditional probabilities are similarly estimated. For example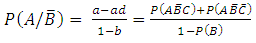 | (17) |
and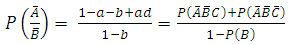 | (18) |
which are the weighted sums of the corresponding marginal probabilities of occurrence of events 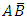 and
and 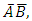 respectively; etc.Having obtained estimates of the probabilities or odds of infection in the population, the researcher may then also wish to estimate the number of the susceptible population of interest that would be expected to be in the various disease infection classification levels. To do this, assuming that the total number of susceptible in the population is ‘N’, then the researcher would only need to apply ‘N’ to each of the estimated probabilities to obtain the desired number of subjects likely to be infected in each disease classification level; assuming all other factors affecting such diseases in the population have been partialled out.
respectively; etc.Having obtained estimates of the probabilities or odds of infection in the population, the researcher may then also wish to estimate the number of the susceptible population of interest that would be expected to be in the various disease infection classification levels. To do this, assuming that the total number of susceptible in the population is ‘N’, then the researcher would only need to apply ‘N’ to each of the estimated probabilities to obtain the desired number of subjects likely to be infected in each disease classification level; assuming all other factors affecting such diseases in the population have been partialled out.
3. Illustrative Example
The proposed method is ideally used especially where the prevalence rates of conditions such as diseases in a population are know and some of the interrelationships between the diseases are also known or can be determined. As already noted above, it is of course also possible to assign and fit some probability distributions to the diseases or families of diseases and then estimate desired marginal, joint, and conditional probabilities of occurrence of these diseases. This approach would however be rather tedious in most applications. We will here therefore for illustrative purposes only, assume that the diseases or families of diseases of interest A, B, and C can without loss of generality be assigned probability of occurrence in a population and that some of the conditional probabilities of occurrence of the diseases are also known or can be determined in a population with ‘N’ equal 1,000,000 subjects susceptible to the diseases. Specifically, suppose it is known that 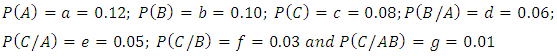 Now using this information, we would estimate that the probability that a randomly selected subject from the population is infected simultaneously by the three diseases A, B, and C is
Now using this information, we would estimate that the probability that a randomly selected subject from the population is infected simultaneously by the three diseases A, B, and C is 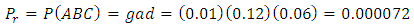 The corresponding number of subjects in the hypothetical population expected to be infected simultaneously by the three diseases is therefore
The corresponding number of subjects in the hypothetical population expected to be infected simultaneously by the three diseases is therefore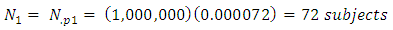 The probability that a randomly selected subject from the population is not infected simultaneously by the three diseases is
The probability that a randomly selected subject from the population is not infected simultaneously by the three diseases is 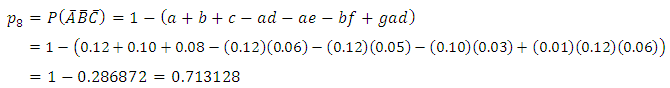 Hence the number of subjects in the population expected not to be infected by the three diseases simultaneously is
Hence the number of subjects in the population expected not to be infected by the three diseases simultaneously is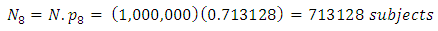 Other estimated joint probabilities of infection shown in Table 2 and the corresponding number of subjects in the population expected to be so infected are similarly calculated and the results are shown in Table 3, where the number of infected subjects are shown in parenthesis.
Other estimated joint probabilities of infection shown in Table 2 and the corresponding number of subjects in the population expected to be so infected are similarly calculated and the results are shown in Table 3, where the number of infected subjects are shown in parenthesis.Table 3. Estimated Joint Probabilities of Infection and Numbers of Infected Subjects for Table 2 under the assumed Disease Prevalence Rates in a Population
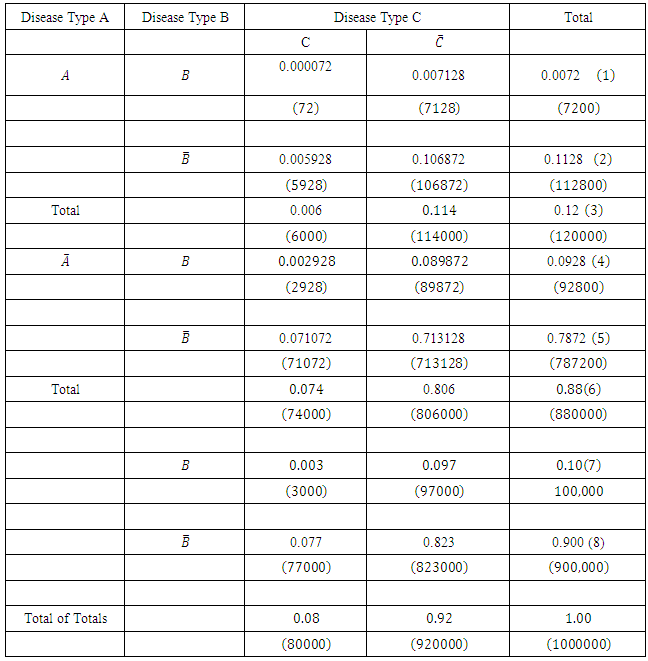 |
| |
|
Now the probability that a randomly selected subject is infected with only one of the three diseases, from Tables 2, and 3 With the estimated number of infected subjects given as
With the estimated number of infected subjects given as 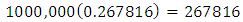 The probability that a randomly selected subjects from the population is affected by only two of the three diseases is similarly obtained from Tables 2 and 3 as
The probability that a randomly selected subjects from the population is affected by only two of the three diseases is similarly obtained from Tables 2 and 3 as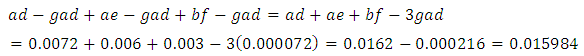 With the estimated number of subjects so infected in the population as
With the estimated number of subjects so infected in the population as 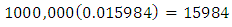 Also the probability that a randomly selected subject from the population who is known to have in the recent past not been infected with two A and B say of the three families of the diseases is currently not free from infection with any of the remaining disease C say is obtained using the entries in Table 3 in Equation 11 as
Also the probability that a randomly selected subject from the population who is known to have in the recent past not been infected with two A and B say of the three families of the diseases is currently not free from infection with any of the remaining disease C say is obtained using the entries in Table 3 in Equation 11 as 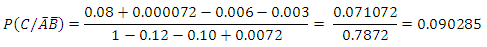 And the expected number of subjects so affected is 90285 We have also estimated using Equation 12 and the values in Table 3 that a randomly selected subject who is already infected by any two of the diseases is currently free from infection with the third disease is
And the expected number of subjects so affected is 90285 We have also estimated using Equation 12 and the values in Table 3 that a randomly selected subject who is already infected by any two of the diseases is currently free from infection with the third disease is  The corresponding number of subjects in the population so infected is
The corresponding number of subjects in the population so infected is 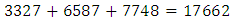 Use of Equation 13 and Table 3 enables the calculation of the probability that a randomly selected subject who is known to be free from infection with any two of the three diseases is currently infected with only one of them as
Use of Equation 13 and Table 3 enables the calculation of the probability that a randomly selected subject who is known to be free from infection with any two of the three diseases is currently infected with only one of them as 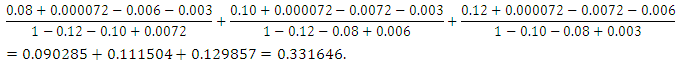 The corresponding number of affected subjects is
The corresponding number of affected subjects is 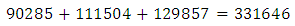 Also from Equation 14 and Table 3, we calculate that the probability that a randomly selected subject from the population who is known to have in the recent past been infected with any two A and B say of the three families of the diseases is currently free from infection with the remaining one C say is
Also from Equation 14 and Table 3, we calculate that the probability that a randomly selected subject from the population who is known to have in the recent past been infected with any two A and B say of the three families of the diseases is currently free from infection with the remaining one C say is 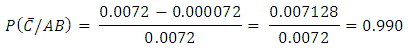 with 990000 subjects so affected.Other odds of infection of interest and the corresponding number of subjects so affected in the population may be similarly estimated.
with 990000 subjects so affected.Other odds of infection of interest and the corresponding number of subjects so affected in the population may be similarly estimated.
4. Summary and Conclusions
In this paper, we have developed and presented a statistical method for the estimation of the joint, marginal and conditional probabilities that a randomly selected subject from a given population would be infected or not infected with two or three diseases or families of diseases either simultaneously or in progression as well as the expected numbers of subjects so infected or not infected in the population assuming no prior remedial actions are taken to influence disease outcome. Although an alternative approach to this problem could be fitting of some hypothesized probability distributions to available data on disease prevalence in a population and then estimating desired probabilities, the proposed method is rather less tedious to apply in practice and the results relatively easier to interpret and explain.In the absence of readily available data on disease prevalence rates, the proposed method is illustrated with assumed prevalence rates of three diseases that may exist in a population.
References
| [1] | Andersons, R. M ed (1982): Population dynamic of Infectious Diseases: Theory and Applications. Chapman and Hall, London. New York. |
| [2] | Andersons, R. M and May, R.M (1991): Infectious Diseases of Humans: Oxford. Oxford Uni. Press. |
| [3] | Bernoulli, D and Blower, S. (2004): An attempt at a new analysis of the mortality caused by smallpox and of the advantages of inoculation to prevent it. Review in Medical Virology, 14, 225-288. |
| [4] | Blower, S.M, Mclean, A.R., Panco, T.C; Small, P.M; Hopewell, P.C; Sanchez, M.A; et al (1995): The intrinsic transmission dynamics of tuberculosis epidemics. “Nature Medicine’, 815-821. |
| [5] | Brauer, F and Castillo-Chavez, C. (2001): Mathematical models in Population Biology and Epidemiology, N.Y. Springer. |
| [6] | Commun. Statist. TheoryMeth.A9(17), 1749-1874. |
| [7] | Conover, W.J (1980): Practical Non-Parametric Statistics 2nd ed. John Wiley and Sons Inc, New York, N.Y. |
| [8] | Daley, D.T and Gani, J. (2005): Epidemic modeling; An Introduction. N. Y. Cambridge Uni. Press. |
| [9] | Hastie, J.J, Tibshirani, R.J. (1987): Generalised Additive Models. Some Applications. J. Am. Stat. Assoc. , 82, 371-86. |
| [10] | Hastie, JJ, Tibshirani, RJ. (1990): Generalised Additive models. London, UK Chapman and Hall ltd. |
| [11] | Heshcote, H.W (2000): The mathematics of infectious diseases. Society for industrial and applied mathematics, 42, 599-653. |
| [12] | Imen, R.L. and Conover, W.J (1982): Small sample sensitivity analysis techniques for computer models with an application to risk assessment. |
| [13] | Kendall, M and Stewart, A. (1979): The advance theory of statistics, Vol 11. Hafner publishing company, New York. |
| [14] | Trotier, H.C and Philippe, P. (2001): Deterministic modeling of infectious diseases theory and methods. The Internet Journal of Infectious Disease. |
| [15] | Zhao LP, Kristal AR, White E. (1996) Estimating relative risk functions in case-control studies using a non parametric logistic regression. Am J. Epidemiology 144, 598-609. |



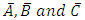 be the possibility that a randomly selected subject or individual may not be infected with disease A, B and C respectively. Let ABC be the possibility that a randomly selected subject from the population is infected by all the diseases in the three disease groups. Let
be the possibility that a randomly selected subject or individual may not be infected with disease A, B and C respectively. Let ABC be the possibility that a randomly selected subject from the population is infected by all the diseases in the three disease groups. Let 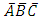 be the possibility that a randomly selected subject from the population is not infected with any of the three diseases. Let
be the possibility that a randomly selected subject from the population is not infected with any of the three diseases. Let 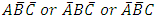 be the possibility that a randomly selected subject from the population is infected with only one of the three diseases. Let also
be the possibility that a randomly selected subject from the population is infected with only one of the three diseases. Let also 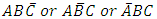 be the possibility that a randomly selected subject from the population is infected by only two of the three diseases.Hence possible configurations of the occurrence of these diseases in a subject and in the population may be presented as in Table 1.
be the possibility that a randomly selected subject from the population is infected by only two of the three diseases.Hence possible configurations of the occurrence of these diseases in a subject and in the population may be presented as in Table 1.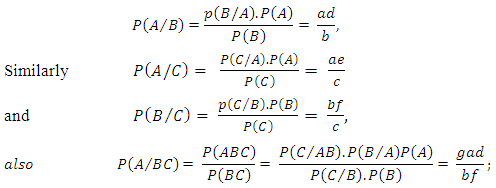
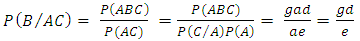
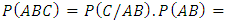
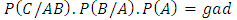 .The probability that a randomly selected subject from the population is not infected with any of the three diseases, that is in disease condition
.The probability that a randomly selected subject from the population is not infected with any of the three diseases, that is in disease condition 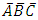 is
is 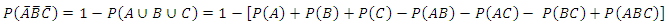
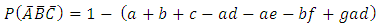
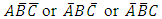 is from Table 2
is from Table 2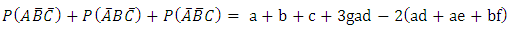

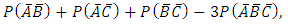 where
where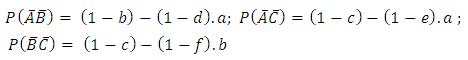
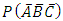 is given in Equation 3.The probability that a randomly selected subject from the population is affected by only two of the three diseases; that is the probability of the events
is given in Equation 3.The probability that a randomly selected subject from the population is affected by only two of the three diseases; that is the probability of the events 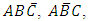 and
and  may be similarly obtained as the sum of the values of the probabilities of these events in Table 2 as
may be similarly obtained as the sum of the values of the probabilities of these events in Table 2 as 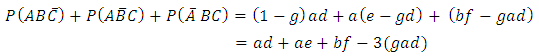
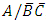 , that is
, that is 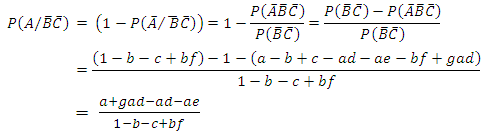
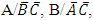 and
and 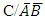 which is calculated as
which is calculated as 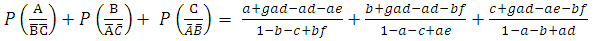
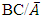 which is estimated as
which is estimated as 
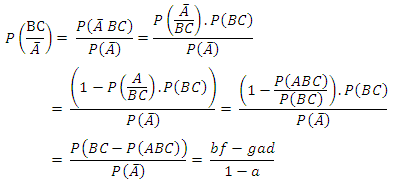 Hence the probability that a randomly selected subject is infected by any two of the family of diseases given that the subject has been cured or has immunity against the other family of diseases is the probability of the events
Hence the probability that a randomly selected subject is infected by any two of the family of diseases given that the subject has been cured or has immunity against the other family of diseases is the probability of the events 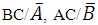 and ,
and , 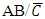 which is estimated as the probability
which is estimated as the probability 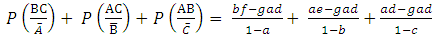
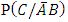 which is given as
which is given as 
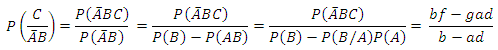 Hence the probability that a randomly selected subject from the population is currently infected with one of the diseases in three families of diseases given that the subject had earlier been infected with diseases in one of the remaining families is the probability of the events
Hence the probability that a randomly selected subject from the population is currently infected with one of the diseases in three families of diseases given that the subject had earlier been infected with diseases in one of the remaining families is the probability of the events 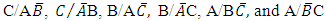 which is calculated as
which is calculated as 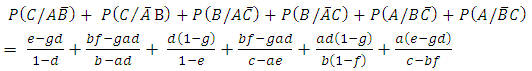
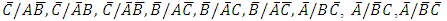 The probability is easily obtained using the estimates in Table 2 and Equation 5 as
The probability is easily obtained using the estimates in Table 2 and Equation 5 as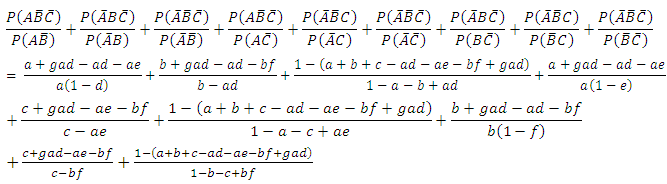
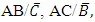 and
and 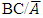 which is given as
which is given as 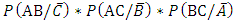 or equivalently using the result of Table 2
or equivalently using the result of Table 2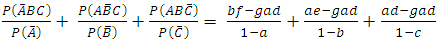
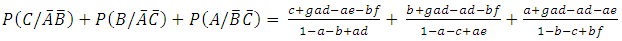
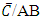 which is calculated using the value in Table 2 as
which is calculated using the value in Table 2 as
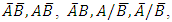 etc. The probabilities can easily be obtained from Table 2 as the sum of the joint probabilities of occurrence or non occurrence of events or diseases A and B summed over events C and
etc. The probabilities can easily be obtained from Table 2 as the sum of the joint probabilities of occurrence or non occurrence of events or diseases A and B summed over events C and 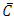 , that is the marginal probabilities of occurrence or non occurrence of the compound event AB, say. Thus
, that is the marginal probabilities of occurrence or non occurrence of the compound event AB, say. Thus 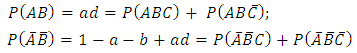
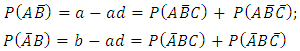
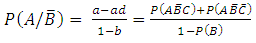
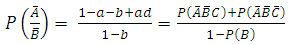
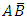 and
and 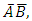 respectively; etc.Having obtained estimates of the probabilities or odds of infection in the population, the researcher may then also wish to estimate the number of the susceptible population of interest that would be expected to be in the various disease infection classification levels. To do this, assuming that the total number of susceptible in the population is ‘N’, then the researcher would only need to apply ‘N’ to each of the estimated probabilities to obtain the desired number of subjects likely to be infected in each disease classification level; assuming all other factors affecting such diseases in the population have been partialled out.
respectively; etc.Having obtained estimates of the probabilities or odds of infection in the population, the researcher may then also wish to estimate the number of the susceptible population of interest that would be expected to be in the various disease infection classification levels. To do this, assuming that the total number of susceptible in the population is ‘N’, then the researcher would only need to apply ‘N’ to each of the estimated probabilities to obtain the desired number of subjects likely to be infected in each disease classification level; assuming all other factors affecting such diseases in the population have been partialled out. 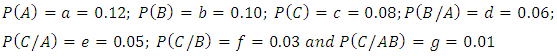 Now using this information, we would estimate that the probability that a randomly selected subject from the population is infected simultaneously by the three diseases A, B, and C is
Now using this information, we would estimate that the probability that a randomly selected subject from the population is infected simultaneously by the three diseases A, B, and C is 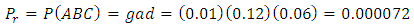 The corresponding number of subjects in the hypothetical population expected to be infected simultaneously by the three diseases is therefore
The corresponding number of subjects in the hypothetical population expected to be infected simultaneously by the three diseases is therefore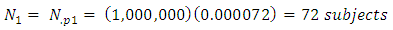 The probability that a randomly selected subject from the population is not infected simultaneously by the three diseases is
The probability that a randomly selected subject from the population is not infected simultaneously by the three diseases is 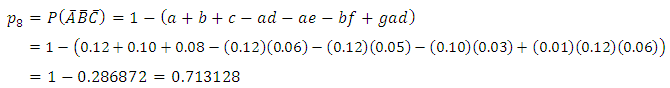 Hence the number of subjects in the population expected not to be infected by the three diseases simultaneously is
Hence the number of subjects in the population expected not to be infected by the three diseases simultaneously is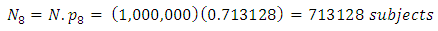 Other estimated joint probabilities of infection shown in Table 2 and the corresponding number of subjects in the population expected to be so infected are similarly calculated and the results are shown in Table 3, where the number of infected subjects are shown in parenthesis.
Other estimated joint probabilities of infection shown in Table 2 and the corresponding number of subjects in the population expected to be so infected are similarly calculated and the results are shown in Table 3, where the number of infected subjects are shown in parenthesis. With the estimated number of infected subjects given as
With the estimated number of infected subjects given as 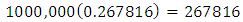 The probability that a randomly selected subjects from the population is affected by only two of the three diseases is similarly obtained from Tables 2 and 3 as
The probability that a randomly selected subjects from the population is affected by only two of the three diseases is similarly obtained from Tables 2 and 3 as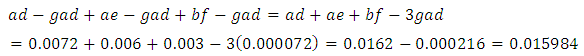 With the estimated number of subjects so infected in the population as
With the estimated number of subjects so infected in the population as 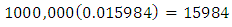 Also the probability that a randomly selected subject from the population who is known to have in the recent past not been infected with two A and B say of the three families of the diseases is currently not free from infection with any of the remaining disease C say is obtained using the entries in Table 3 in Equation 11 as
Also the probability that a randomly selected subject from the population who is known to have in the recent past not been infected with two A and B say of the three families of the diseases is currently not free from infection with any of the remaining disease C say is obtained using the entries in Table 3 in Equation 11 as 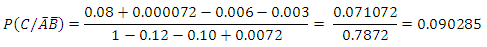 And the expected number of subjects so affected is 90285 We have also estimated using Equation 12 and the values in Table 3 that a randomly selected subject who is already infected by any two of the diseases is currently free from infection with the third disease is
And the expected number of subjects so affected is 90285 We have also estimated using Equation 12 and the values in Table 3 that a randomly selected subject who is already infected by any two of the diseases is currently free from infection with the third disease is  The corresponding number of subjects in the population so infected is
The corresponding number of subjects in the population so infected is 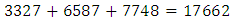 Use of Equation 13 and Table 3 enables the calculation of the probability that a randomly selected subject who is known to be free from infection with any two of the three diseases is currently infected with only one of them as
Use of Equation 13 and Table 3 enables the calculation of the probability that a randomly selected subject who is known to be free from infection with any two of the three diseases is currently infected with only one of them as 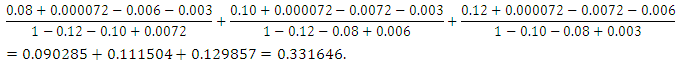 The corresponding number of affected subjects is
The corresponding number of affected subjects is 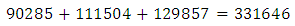 Also from Equation 14 and Table 3, we calculate that the probability that a randomly selected subject from the population who is known to have in the recent past been infected with any two A and B say of the three families of the diseases is currently free from infection with the remaining one C say is
Also from Equation 14 and Table 3, we calculate that the probability that a randomly selected subject from the population who is known to have in the recent past been infected with any two A and B say of the three families of the diseases is currently free from infection with the remaining one C say is 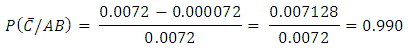 with 990000 subjects so affected.Other odds of infection of interest and the corresponding number of subjects so affected in the population may be similarly estimated.
with 990000 subjects so affected.Other odds of infection of interest and the corresponding number of subjects so affected in the population may be similarly estimated. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

