-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2015; 5(6): 354-360
doi:10.5923/j.ajms.20150506.03

On Size Biased Poisson - Lindley Distribution and Its Applications to Model Thunderstorms
Rama Shanker1, Hagos Fesshaye2, Abrehe Yemane1
1Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea
2Department of Economics, College of Business and Economics, Halhale, Eritrea
Correspondence to: Rama Shanker, Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper firstly a general expression for the rth factorial moment of size biased Poisson-Lindley distribution (SBPLD) has been obtained and hence its first four moments about origin have been given. The expression for moment generating function and the first inverse moment of SBPLD has also been obtained. To test the goodness of fit of SBPLD over size-biased Poisson distribution (SBPD) for modeling thunderstorms, SBPLD has been fitted to a number of data sets related to thunderstorms using maximum likelihood estimate and it has been found that SBPLD gives much closer fit than SBPD, and thus SBPLD can be considered as an important alternative tool for modeling thunderstorms.
Keywords: Poisson-Lindley distribution, Size-Biased distribution, Inverse moment, Estimation of parameter, Thunderstorms, Goodness of fit
Cite this paper: Rama Shanker, Hagos Fesshaye, Abrehe Yemane, On Size Biased Poisson - Lindley Distribution and Its Applications to Model Thunderstorms, American Journal of Mathematics and Statistics, Vol. 5 No. 6, 2015, pp. 354-360. doi: 10.5923/j.ajms.20150506.03.
Article Outline
1. Introduction
- Size-biased distributions arise in practice when observations from a sample are recorded with unequal probabilities, having probability proportional to some measure of unit size. These distributions were firstly introduced by Fisher (1934) to model ascertainment biases which were later formalized by Rao (1965) in a unifying theory. Van Deusen (1986) discussed size-biased distribution theory and applied it to fitting distributions of diameter at breast height (DBH) data arising from horizontal point sampling (HPS). Later, Lappi and Bailey (1987) used size-biased distributions to analyze HPS diameter increment data. Most of the statistical applications of size biased distributions, especially to the analysis of data relating to human population and ecology, can be found in Patil and Rao (1977, 1978). Some of the recent results on size-biased distributions pertaining to parameter estimation in forestry with special emphasis on Weibull family have been reviewed by Gove (2003).If a random variable X have distribution
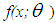 then a simple size-biased distribution is defined by its probability function
then a simple size-biased distribution is defined by its probability function 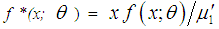 , where
, where 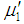 is the mean of the original distribution. In this paper, a general expression for the rth factorial moment of size-biased Poisson-Lindley distribution (SBPLD) has been obtained and hence its first four moments about origin has been derived. The expression for moment generating function and the first inverse moment has also been obtained. It seems that no work has been done on the applications of SBPLD to model thunderstorms. The SBPLD has been fitted to some data sets related to thunderstorms to test its goodness of fit over SBPD and it has been found that SBPLD provides much closer fit than SBPD. This shows that the SBPLD is more flexible than SBPD for modeling thunderstorms.
is the mean of the original distribution. In this paper, a general expression for the rth factorial moment of size-biased Poisson-Lindley distribution (SBPLD) has been obtained and hence its first four moments about origin has been derived. The expression for moment generating function and the first inverse moment has also been obtained. It seems that no work has been done on the applications of SBPLD to model thunderstorms. The SBPLD has been fitted to some data sets related to thunderstorms to test its goodness of fit over SBPD and it has been found that SBPLD provides much closer fit than SBPD. This shows that the SBPLD is more flexible than SBPD for modeling thunderstorms.2. Size-Biased Poisson-Lindley Distribution (SBPLD)
- A size biased Poisson-Lindley distribution (SBPLD) given by its probability mass function (pmf)
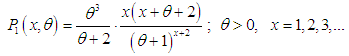 | (2.1) |
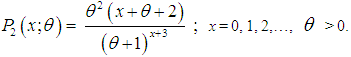 | (2.2) |
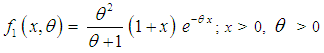 | (2.3) |
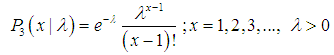 | (2.4) |
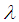 follows the size biased Lindley distribution (SBLD) with pdf
follows the size biased Lindley distribution (SBLD) with pdf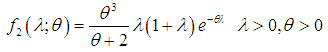 | (2.5) |
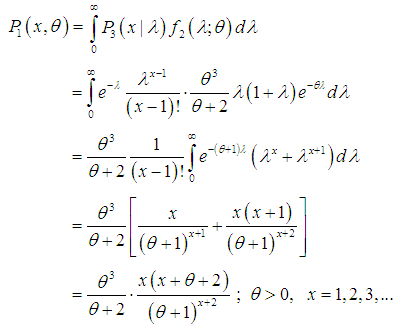 | (2.6) |
3. Moments
- The rth factorial moment of the SBPLD (2.1) can be obtained as
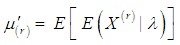 | (3.1) |
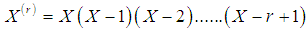 .From (2.6), we get
.From (2.6), we get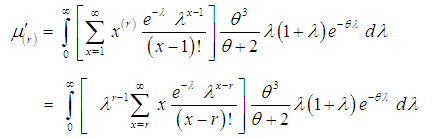 | (3.2) |
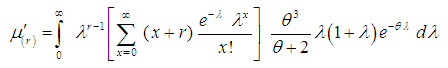 The expression within bracket is clearly
The expression within bracket is clearly 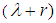 and hence we have
and hence we have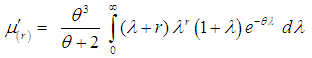 | (3.3) |
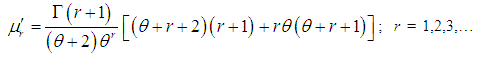 | (3.4) |
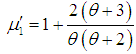 | (3.5) |
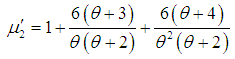 | (3.6) |
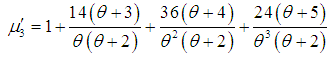 | (3.7) |
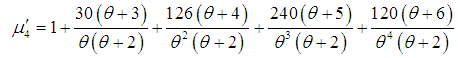 | (3.8) |
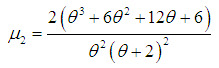 | (3.9) |
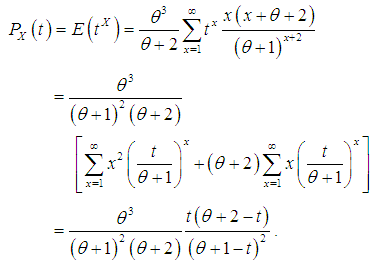 The moment generating function of SBPLD is thus obtained as
The moment generating function of SBPLD is thus obtained as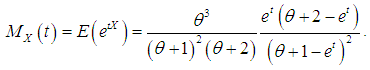 .First Inverse Moment: The first inverse moment of SBPLD is given by
.First Inverse Moment: The first inverse moment of SBPLD is given by 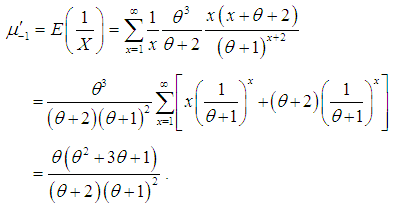
4. Estimation of Parameters
4.1. Maximum Likelihood (ML) Estimates
- Let
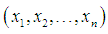 be a random sample of size n from the SBPLD (2.1). Let
be a random sample of size n from the SBPLD (2.1). Let 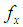 be the observed frequency in the sample corresponding to
be the observed frequency in the sample corresponding to 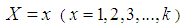 such that
such that 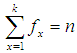 , where
, where 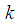 is the largest observed value having non-zero frequency. The likelihood function,
is the largest observed value having non-zero frequency. The likelihood function, 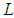 , of the SBPLD (2.1) is given by
, of the SBPLD (2.1) is given by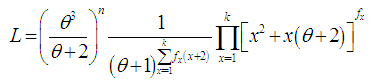 The log likelihood function is given by
The log likelihood function is given by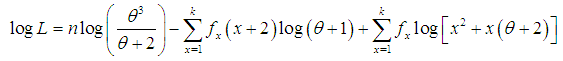 The maximum likelihood estimate,
The maximum likelihood estimate, 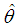 of
of 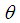 is the solution of the equation
is the solution of the equation 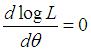 and is given by solution of the following non-linear equation
and is given by solution of the following non-linear equation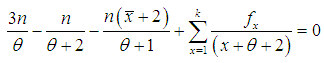 | (4.1.1) |
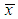 is the sample mean. It has been shown by Ghitany and Mutairi (2008) that the ML estimator
is the sample mean. It has been shown by Ghitany and Mutairi (2008) that the ML estimator 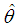 of
of 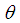 is consistent and asymptotically normal.
is consistent and asymptotically normal. 4.2. Estimates from Moments
- Let
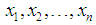 be a random sample of size n from the SBPLD (2.1). Equating the first moment about origin to the sample mean, the method of moment (MOM) estimate,
be a random sample of size n from the SBPLD (2.1). Equating the first moment about origin to the sample mean, the method of moment (MOM) estimate, 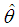 , of
, of 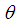 is given by
is given by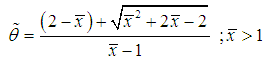 | (4.2.1) |
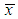 is the sample mean. It has been shown by Ghitany and Mutairi (2008) that the MOM estimator
is the sample mean. It has been shown by Ghitany and Mutairi (2008) that the MOM estimator 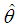 of
of 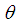 is positively biased, consistent and asymptotically normal.
is positively biased, consistent and asymptotically normal.5. Applications of SBPLD to Model Thunderstorms
- The Poisson distribution is a suitable model for the situations where events seem to occur at random such as the number of customers arriving at a service point, the number of telephone calls arriving at an exchange , the number of fatal traffic accidents per week in a given state, the number of radioactive particle emissions per unit of time, the number of meteorites that collide with a test satellite during a single orbit, the number of organisms per unit volume of some fluid, the number of defects per unit of some materials, the number of flaws per unit length of some wire, etc. However, the Poisson distribution requires events to be independent- a condition which is rarely satisfied completely. In thunderstorm activity, the occurrence of successive thunderstorm events (THE’s) is often dependent process meaning that the occurrence of a THE indicates that the atmosphere is unstable and the conditions are favorable for the formation of further thunderstorm activity. The negative binomial distribution (NBD) is a possible alternative to the Poisson distribution when successive events are possibly dependent [see Johnson et al, 2005]. The theoretical and empirical justification for using the NBD to describe THE activity has been fully explained and discussed by Falls et al (1971). Further, for fitting Poisson distribution to the count data equality of mean and variance should be satisfied. Similarly, for fitting NBD to the count data, mean should be less than the variance. In THE, these conditions are not fully satisfied. As a model to describe the frequencies of thunderstorms (TH’s), given an occurrence of THE, the size biased Poisson distribution (SBPD) or zero truncated Poisson distribution (ZTPD) can be considered. But ZTPD does not give satisfactory fit to THE due to the basic assumption that events are independent with stable probabilities. Further, SBPD also does not give satisfactory fit due to the reason that it is under- dispersed
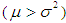 .The theoretical and empirical justification for the selection of the SBPLD to describe THE activity is that SBPLD is over-dispersed
.The theoretical and empirical justification for the selection of the SBPLD to describe THE activity is that SBPLD is over-dispersed 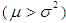 , equi-dispersed
, equi-dispersed 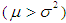 , and under-dispersed
, and under-dispersed 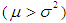 for
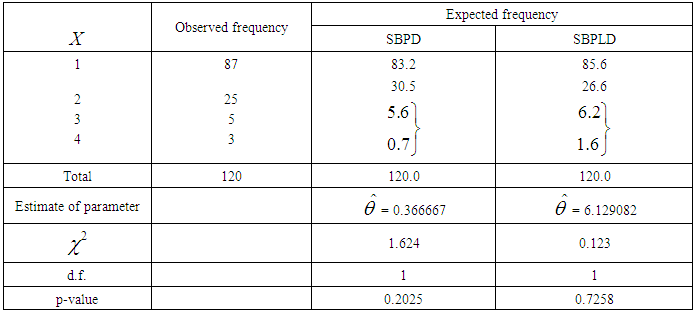
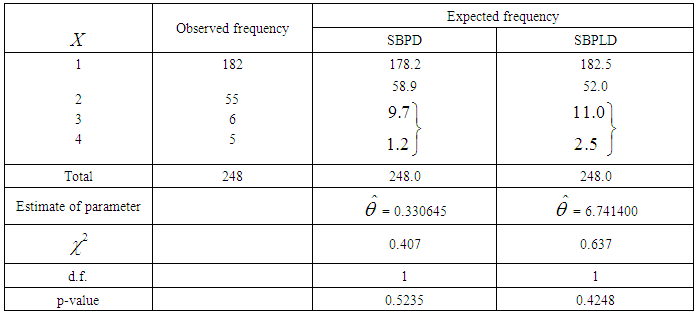
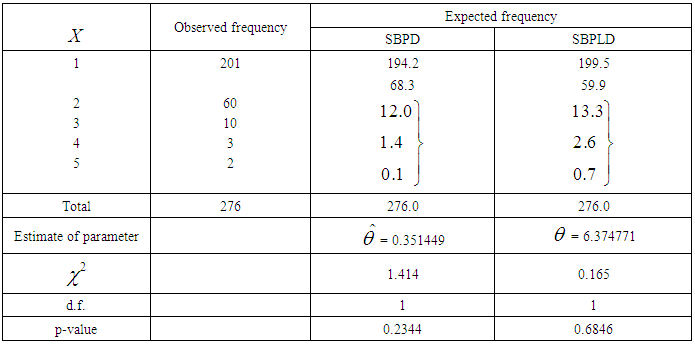
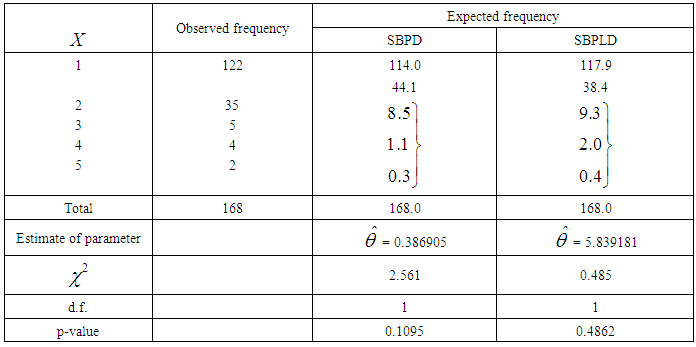
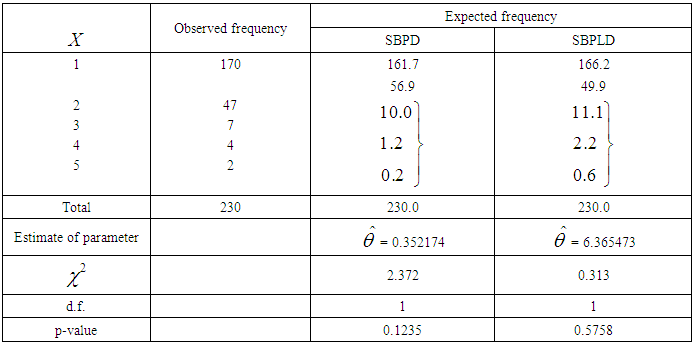
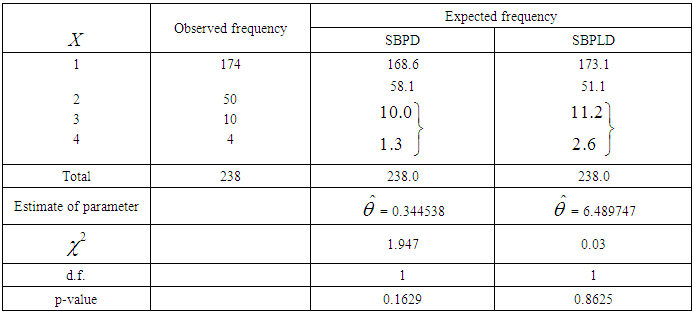
for 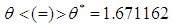 respectively.The data for thunderstorms activity at Cape Kennedy, Florida and immediate surroundings for the period January 1957 to December 1967, reported by Carter (2001), has been used for showing the applications of SBPLD and SBPD to model thunderstorms.The expected frequencies according to the SBPD have also been given in these tables for ready comparison with those obtained by the SBPLD. The estimate of the parameter has been obtained by the maximum likelihood estimation.It can be seen that the SBPLD gives much closer fits than the SBPD and thus provides a better alternative to the SBPD and it can be recommended for modeling thunderstorm events.
respectively.The data for thunderstorms activity at Cape Kennedy, Florida and immediate surroundings for the period January 1957 to December 1967, reported by Carter (2001), has been used for showing the applications of SBPLD and SBPD to model thunderstorms.The expected frequencies according to the SBPD have also been given in these tables for ready comparison with those obtained by the SBPLD. The estimate of the parameter has been obtained by the maximum likelihood estimation.It can be seen that the SBPLD gives much closer fits than the SBPD and thus provides a better alternative to the SBPD and it can be recommended for modeling thunderstorm events.
|
|
|
|
|
|
6. Conclusions
- In this paper, a general expression for the
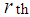 factorial moment of SBPLD has been obtained and hence first four moments about origin has been given. The expressions for moment generating function and the first inverse moment has also been derived. To test the applicability and superiority of SBPLD over SBPD for modeling thunderstorms, SBPLD has been fitted to a number of data sets related to thunderstorms and it has been found that it provides a much closer fit than SBPD and hence it is recommended to be an important tool for modeling thunderstorms.
factorial moment of SBPLD has been obtained and hence first four moments about origin has been given. The expressions for moment generating function and the first inverse moment has also been derived. To test the applicability and superiority of SBPLD over SBPD for modeling thunderstorms, SBPLD has been fitted to a number of data sets related to thunderstorms and it has been found that it provides a much closer fit than SBPD and hence it is recommended to be an important tool for modeling thunderstorms.ACKNOWLEDGEMENTS
- The authors are grateful for the constructive suggestions of the anonymous reviewer.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML