Jian Ye
Department of Mathematics Sichuan University, Chengdu, China
Correspondence to: Jian Ye, Department of Mathematics Sichuan University, Chengdu, China.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The Goldbach theorem and the twin prime theorem are homologous. The paper from the prime origin, derived the equations of the twin prime theorem and the Goldbach theorem, and new prime number theorem.
Keywords:
the Goldbach Theorem, the Twin Prime Theorem, Prime Number Theorem
Cite this paper: Jian Ye, The Distribution of Prime Numbers in an Interval, American Journal of Mathematics and Statistics, Vol. 5 No. 6, 2015, pp. 325-328. doi: 10.5923/j.ajms.20150506.01.
1. Notation
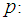 a prime number. p: an odd prime.
a prime number. p: an odd prime. 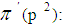 the number of primes in the open interval
the number of primes in the open interval 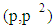 .
. 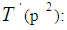 the number of twin prime pairs
the number of twin prime pairs 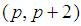 in the open interval
in the open interval 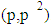 .
. 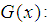 the number of prime
the number of prime 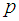 in the open interval
in the open interval 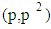 . p is the largest prime number less than
. p is the largest prime number less than 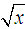 , and
, and 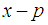 is prime number,
is prime number, 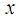 is a large even integer.
is a large even integer. 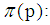 denotes not more than p of prime numbers.
denotes not more than p of prime numbers. 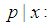
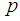 divides
divides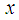 .
. 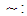 denotes equialence relation.
denotes equialence relation. 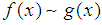 , namely:
, namely: 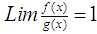 , when
, when 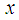 tends to infinity.
tends to infinity. 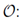 mean big O notation describes the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions.
mean big O notation describes the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. 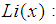 express the logarithmic integral function or integral logarithm
express the logarithmic integral function or integral logarithm 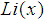 is a special function such as
is a special function such as 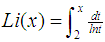 .
.
2. Prime Number Theorem [1] [2]
Let 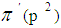 is the number of primes in the open interval
is the number of primes in the open interval 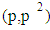 . p is an odd prime,
. p is an odd prime, 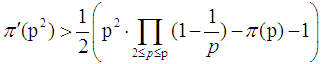 | (1) |
where 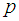 is a prime number.
is a prime number. 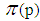 is not more than p of prime numbers. Lemma 1Let
is not more than p of prime numbers. Lemma 1Let 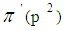 is the number of primes in the open interval
is the number of primes in the open interval 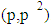 . p is an odd prime, Let
. p is an odd prime, Let 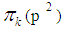 is the number of odd
is the number of odd 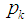 between
between 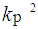 to
to 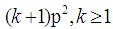 and
and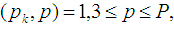
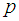 is a prime number, p is an odd prime, Let
is a prime number, p is an odd prime, Let 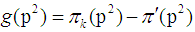
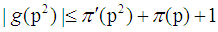 | (2) |
where 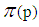 is not more than p of prime numbers. The proof of lemma 1Reduction to absurdity. The proof of prime number theoremProof By lemma 1 and Chinese remainder theorem, it can be derived
is not more than p of prime numbers. The proof of lemma 1Reduction to absurdity. The proof of prime number theoremProof By lemma 1 and Chinese remainder theorem, it can be derived 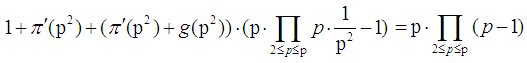 | (3) |
Hence proving 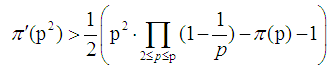 where
where 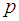 is a prime number.
is a prime number. 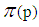 is not more than p of prime numbers.
is not more than p of prime numbers.
3. The Twin Prime Theorem
Let 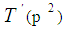 is the number of twin prime pairs
is the number of twin prime pairs 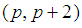 in the open interval
in the open interval 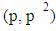 , p is an odd prime,
, p is an odd prime, 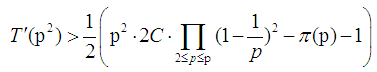 | (4) |
where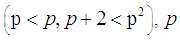 is a prime number.
is a prime number. 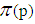 is not more than p of prime numbers. Among which
is not more than p of prime numbers. Among which 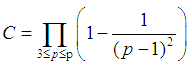 | (5) |
Lemma 2Let 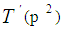 is the number of twin prime pairs
is the number of twin prime pairs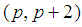 in the open interval
in the open interval 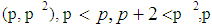 is a prime number, p is an odd prime. Let
is a prime number, p is an odd prime. Let 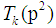 is the number of the odd
is the number of the odd 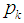 between
between 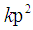 to
to 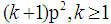 and
and 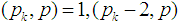
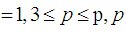 is a prime number.p is an odd prime. Let
is a prime number.p is an odd prime. Let 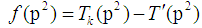
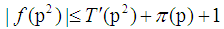 | (6) |
Where 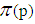 is not more than p of prime numbers. The proof of lemma 2Reduction to absurdity. The proof of twin prime theoremProof By lemma 2 and Chinese remainder theorem,it can be derived
is not more than p of prime numbers. The proof of lemma 2Reduction to absurdity. The proof of twin prime theoremProof By lemma 2 and Chinese remainder theorem,it can be derived 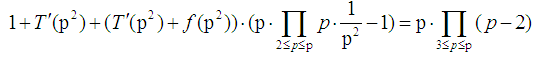 | (7) |
Hence proving 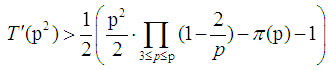 | (8) |
or 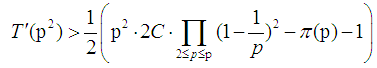 where
where 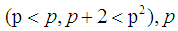 is a prime number.
is a prime number. 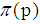 is not more than p of prime numbers. Among which
is not more than p of prime numbers. Among which 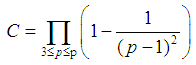
4. The Goldbach Theorem
Let 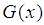 is the number of prime
is the number of prime 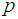 in theopen interval
in theopen interval 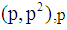 is the largest prime number less than
is the largest prime number less than 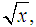 and
and 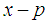 is prime number,
is prime number, 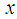 is alarger even integer.
is alarger even integer. 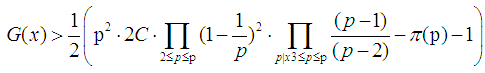 | (9) |
where 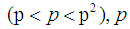 is a prime number.
is a prime number. 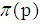 is not more than p of prime numbers. Since
is not more than p of prime numbers. Since 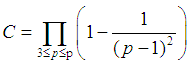 | (10) |
when 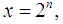
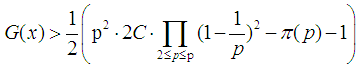 | (11) |
Lemma 3Let 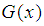 is the number of prime
is the number of prime 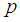 in the open interval
in the open interval 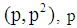 is the largest prime number less than
is the largest prime number less than 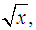 and
and 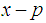 is prime number,
is prime number, 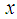 is a large even integer.
is a large even integer. 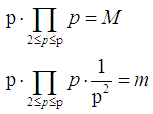 Let
Let 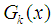 is the number of odd
is the number of odd 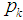 between
between 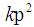 to
to 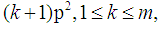 and
and 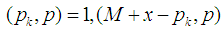
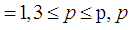 is a prime number, p is the largest prime number less than
is a prime number, p is the largest prime number less than 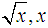 is a large even integer. Let
is a large even integer. Let 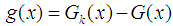
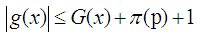 | (12) |
where 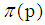 is not more than p of prime numbers. The proof of lemma 3Reduction to absurdity. The proof of the Goldbach theoremProof By lemma 3 and Chinese remainder theorem, it can be derived
is not more than p of prime numbers. The proof of lemma 3Reduction to absurdity. The proof of the Goldbach theoremProof By lemma 3 and Chinese remainder theorem, it can be derived 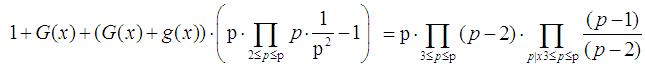 | (13) |
where 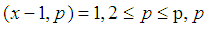 is a prime number. or
is a prime number. or 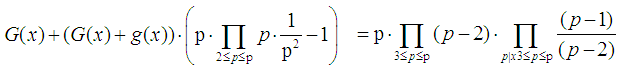 | (14) |
Hence proving 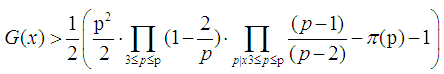 | (15) |
or 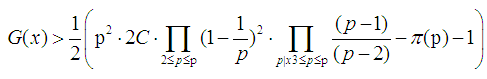 where
where 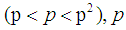 is a prime number.
is a prime number. 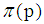 is not more than p of prime numbers. Since
is not more than p of prime numbers. Since 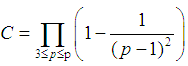 when
when 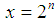 ,
, 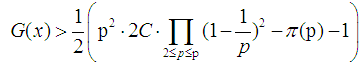
References
| [1] | J.B. Rosser and L. Scloenfeld, approximate formulas for some functions of prime numbers. Lllinois J. Math. Volume 6, Issue 1(1962), 64-94. |
| [2] | G.H. Hardy and E.M. Wright, An Introduction to The Theory of Numbers, section 22.8 and 22.19. The Oxford University Press, 4ed, 1959. |


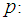 a prime number. p: an odd prime.
a prime number. p: an odd prime. 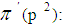 the number of primes in the open interval
the number of primes in the open interval 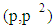 .
. 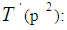 the number of twin prime pairs
the number of twin prime pairs 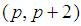 in the open interval
in the open interval 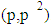 .
. 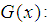 the number of prime
the number of prime 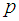 in the open interval
in the open interval 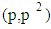 . p is the largest prime number less than
. p is the largest prime number less than 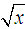 , and
, and 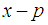 is prime number,
is prime number, 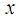 is a large even integer.
is a large even integer. 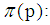 denotes not more than p of prime numbers.
denotes not more than p of prime numbers. 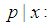
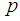 divides
divides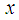 .
. 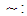 denotes equialence relation.
denotes equialence relation. 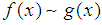 , namely:
, namely: 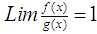 , when
, when 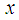 tends to infinity.
tends to infinity. 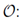 mean big O notation describes the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions.
mean big O notation describes the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. 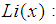 express the logarithmic integral function or integral logarithm
express the logarithmic integral function or integral logarithm 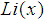 is a special function such as
is a special function such as 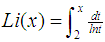 .
. 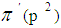 is the number of primes in the open interval
is the number of primes in the open interval 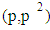 . p is an odd prime,
. p is an odd prime, 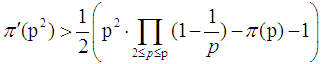
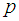 is a prime number.
is a prime number. 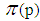 is not more than p of prime numbers. Lemma 1Let
is not more than p of prime numbers. Lemma 1Let 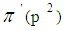 is the number of primes in the open interval
is the number of primes in the open interval 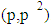 . p is an odd prime, Let
. p is an odd prime, Let 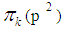 is the number of odd
is the number of odd 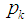 between
between 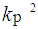 to
to 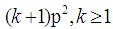 and
and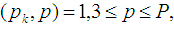
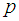 is a prime number, p is an odd prime, Let
is a prime number, p is an odd prime, Let 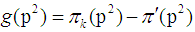
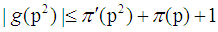
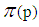 is not more than p of prime numbers. The proof of lemma 1Reduction to absurdity. The proof of prime number theoremProof By lemma 1 and Chinese remainder theorem, it can be derived
is not more than p of prime numbers. The proof of lemma 1Reduction to absurdity. The proof of prime number theoremProof By lemma 1 and Chinese remainder theorem, it can be derived 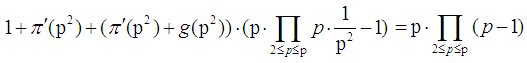
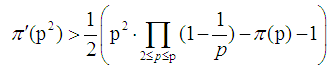 where
where 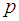 is a prime number.
is a prime number. 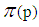 is not more than p of prime numbers.
is not more than p of prime numbers. 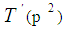 is the number of twin prime pairs
is the number of twin prime pairs 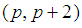 in the open interval
in the open interval 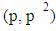 , p is an odd prime,
, p is an odd prime, 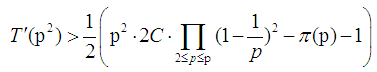
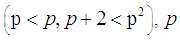 is a prime number.
is a prime number. 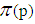 is not more than p of prime numbers. Among which
is not more than p of prime numbers. Among which 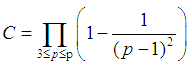
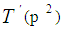 is the number of twin prime pairs
is the number of twin prime pairs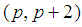 in the open interval
in the open interval 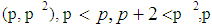 is a prime number, p is an odd prime. Let
is a prime number, p is an odd prime. Let 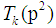 is the number of the odd
is the number of the odd 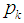 between
between 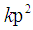 to
to 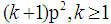 and
and 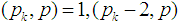
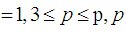 is a prime number.p is an odd prime. Let
is a prime number.p is an odd prime. Let 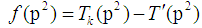
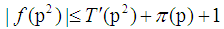
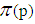 is not more than p of prime numbers. The proof of lemma 2Reduction to absurdity. The proof of twin prime theoremProof By lemma 2 and Chinese remainder theorem,it can be derived
is not more than p of prime numbers. The proof of lemma 2Reduction to absurdity. The proof of twin prime theoremProof By lemma 2 and Chinese remainder theorem,it can be derived 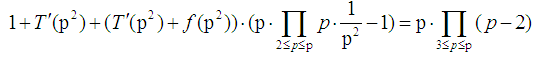
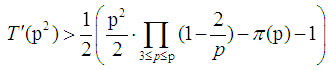
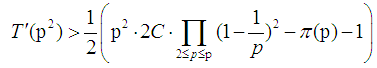 where
where 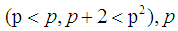 is a prime number.
is a prime number. 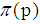 is not more than p of prime numbers. Among which
is not more than p of prime numbers. Among which 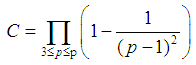
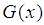 is the number of prime
is the number of prime 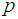 in theopen interval
in theopen interval 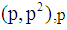 is the largest prime number less than
is the largest prime number less than 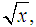 and
and 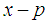 is prime number,
is prime number, 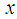 is alarger even integer.
is alarger even integer. 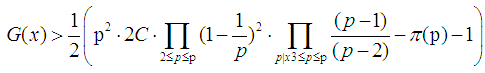
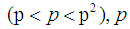 is a prime number.
is a prime number. 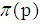 is not more than p of prime numbers. Since
is not more than p of prime numbers. Since 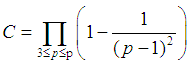
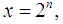
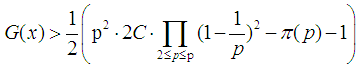
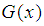 is the number of prime
is the number of prime 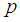 in the open interval
in the open interval 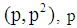 is the largest prime number less than
is the largest prime number less than 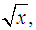 and
and 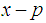 is prime number,
is prime number, 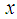 is a large even integer.
is a large even integer. 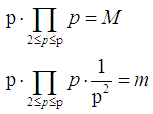 Let
Let 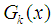 is the number of odd
is the number of odd 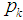 between
between 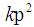 to
to 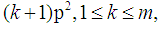 and
and 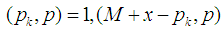
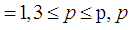 is a prime number, p is the largest prime number less than
is a prime number, p is the largest prime number less than 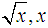 is a large even integer. Let
is a large even integer. Let 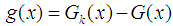
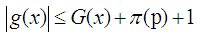
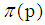 is not more than p of prime numbers. The proof of lemma 3Reduction to absurdity. The proof of the Goldbach theoremProof By lemma 3 and Chinese remainder theorem, it can be derived
is not more than p of prime numbers. The proof of lemma 3Reduction to absurdity. The proof of the Goldbach theoremProof By lemma 3 and Chinese remainder theorem, it can be derived 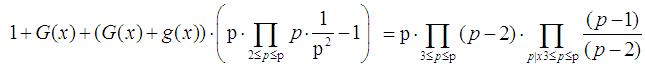
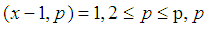 is a prime number. or
is a prime number. or 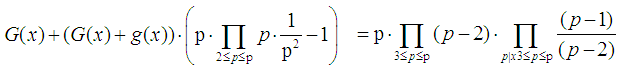
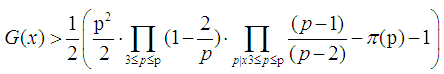
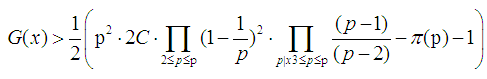 where
where 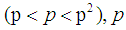 is a prime number.
is a prime number. 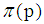 is not more than p of prime numbers. Since
is not more than p of prime numbers. Since 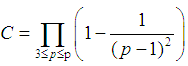 when
when 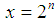 ,
, 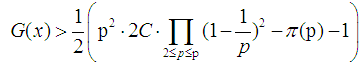
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML