R. C. Leoni1, A. F. B. Costa1, J. W. J. Silva2, 3, N. A. S. Sampaio3, R. B. Ribeiro2, 4
1Universidade Estadual Paulista - UNESP-FEG, Guaratinguetá, SP, Brazil
2Faculdades Integradas Teresa D’Ávila, FATEA, Lorena, SP, Brazil
3Associação Educacional Dom Bosco, AEDB, Resende, RJ, Brazil
4Faculdade de Tecnologia de São Paulo, FATEC, Cruzeiro, SP, Brazil
Correspondence to: J. W. J. Silva, Faculdades Integradas Teresa D’Ávila, FATEA, Lorena, SP, Brazil.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper describes how to plan and estimate the optimal parameters of an adaptive chart to monitor a process average using 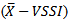 variable sample size and interval. The
variable sample size and interval. The 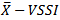 chart was chosen because it is a scheme with great potential for practical application and only requires knowledge of the sample size and the time between sample selection. Markov chains were used to evaluate the chart performance based on the average time between the process uncontrolled and the signal generated by the chart. Two functions written in R language that assist the user in the design of an adaptive control chart
chart was chosen because it is a scheme with great potential for practical application and only requires knowledge of the sample size and the time between sample selection. Markov chains were used to evaluate the chart performance based on the average time between the process uncontrolled and the signal generated by the chart. Two functions written in R language that assist the user in the design of an adaptive control chart 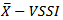 are exhibited.
are exhibited.
Keywords:
Statistical Process Control (SPC), Adaptive Control Chart, Markov Chain, R Language
Cite this paper: R. C. Leoni, A. F. B. Costa, J. W. J. Silva, N. A. S. Sampaio, R. B. Ribeiro, How to Choose Parameters of 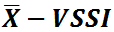 Control Chart with Adaptive Parameters, American Journal of Mathematics and Statistics, Vol. 5 No. 5, 2015, pp. 285-292. doi: 10.5923/j.ajms.20150505.09.
Control Chart with Adaptive Parameters, American Journal of Mathematics and Statistics, Vol. 5 No. 5, 2015, pp. 285-292. doi: 10.5923/j.ajms.20150505.09.
1. Introduction
Control charts are used to monitor production processes aiming to signal deviations in relation to the target of a quality characteristic. Detection of small or moderate deviations by means of charts proposed by Shewhart [1] is time consuming and therefore several types of charts have been proposed. Some authors [2-10] introduced the adaptive control charts which are named this way because they do not present all their fixed parameters. This type of chart construction forecasts that at least one of its parameters may vary. These parameters are: the control limits, the sample size and the time interval in which a sample is collected.In adaptive control charts it is common to use Markov chains to evaluate the chart performance according to the set of chosen parameters [6, 10, 11]. In order to assess the statistical properties, it is used the subjacent idea of dividing the variation interval of monitored statistics in a finite set of states, where the transient states of chain are in the chart control region and the absorbent state is in the established region as out of control.Adaptive charts are not available in traditional statistical software, despite showing better performance than the charts with fixed parameters. Adaptive parameters determination is not a trivial task; thus, this article proposes the use of a free software to plan and estimate the optimal parameters of an adaptive chart for 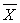 with sample size and interval being variable (
with sample size and interval being variable (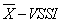 ). The average number of samples until the moment in which the chart indicates the out of control condition (ARL) and the average time between the instant in which the process is changed and the time in which the graph indicates the out of control condition (ATS) are the performance measures used as a reference for the parameters choice. The ARL (Average Run Length) is the average number of points that must be plotted before a point indicates an out-of-control condition, the ATS (Average Time to Signal) represents the average time needed for the control scheme to detect a situation outside of control from the beginning of the process.The
). The average number of samples until the moment in which the chart indicates the out of control condition (ARL) and the average time between the instant in which the process is changed and the time in which the graph indicates the out of control condition (ATS) are the performance measures used as a reference for the parameters choice. The ARL (Average Run Length) is the average number of points that must be plotted before a point indicates an out-of-control condition, the ATS (Average Time to Signal) represents the average time needed for the control scheme to detect a situation outside of control from the beginning of the process.The 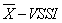 chart was chosen because it is a scheme with great potential for practical application, for its use requires only to know the sample size and the time between samples selection after the optimal parameters are established. The statistical properties of control chart are optimized considering the approach presented by Zimmer [11], that is, a Markov chain is used to establish the parameters keeping under control the statistical risk type I and type II [12].The rest of the paper is organized as follows: section 2 presents the
chart was chosen because it is a scheme with great potential for practical application, for its use requires only to know the sample size and the time between samples selection after the optimal parameters are established. The statistical properties of control chart are optimized considering the approach presented by Zimmer [11], that is, a Markov chain is used to establish the parameters keeping under control the statistical risk type I and type II [12].The rest of the paper is organized as follows: section 2 presents the  control chart. In section 3, it is described the procedure to evaluate the performance of a
control chart. In section 3, it is described the procedure to evaluate the performance of a 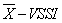 chart using Markov chains. In Section 4, two functions written in R language that assist the user in the design of an adaptive control chart
chart using Markov chains. In Section 4, two functions written in R language that assist the user in the design of an adaptive control chart 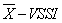 are exhibited. Finally, conclusions and future research directions complete the article.Two functions written in R language that assist the user in the design of an adaptive control chart
are exhibited. Finally, conclusions and future research directions complete the article.Two functions written in R language that assist the user in the design of an adaptive control chart 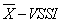 are exhibited.
are exhibited.
2. 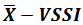 Control Chart
Control Chart
Reynolds [2] was the first to consider the adaptive design of control chart varying the time interval in which a sample is collected. Later there appeared a large number of studies aiming to vary the other control chart parameters, being confirmed that this technique generally increases the chart power on detection of special reasons that modify the average of quality characteristic (variable) to be monitored [9, 10, 12, 13].The 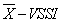 control chart is adaptive with respect to the sample size and the time interval in which a sample is collected. This chart was used by several researchers [3, 4, 9, 10] for monitoring the
control chart is adaptive with respect to the sample size and the time interval in which a sample is collected. This chart was used by several researchers [3, 4, 9, 10] for monitoring the 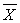 statistics of a process.In a control chart with sample size and interval being variable (see Figure 1) the sample size and time interval in which a sample is taken can vary depending on the information from the most recent sample collected. In this kind of chart, random samples of different sizes are collected in intervals of variable length according to the function:
statistics of a process.In a control chart with sample size and interval being variable (see Figure 1) the sample size and time interval in which a sample is taken can vary depending on the information from the most recent sample collected. In this kind of chart, random samples of different sizes are collected in intervals of variable length according to the function: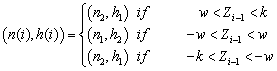 | (1) |
where i=1,2,…, is the number of the sample; 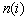 is the size of the ith sample
is the size of the ith sample 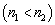 ;
; 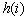 is the time practiced to remove the ith sample
is the time practiced to remove the ith sample 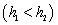 ; k and w are boundaries that define control regions;
; k and w are boundaries that define control regions; 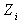 is the control statistics.
is the control statistics.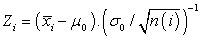 | (2) |
where 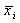 is the sample average of the i-th subgroup;
is the sample average of the i-th subgroup; 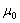 and
and 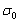 are the mean and standard deviation of the process when in control.The choice between the pairs
are the mean and standard deviation of the process when in control.The choice between the pairs 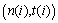 depends on the position of the last point
depends on the position of the last point 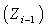 marked on the chart. For a
marked on the chart. For a 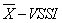 chart, one can divide the control area into three regions mutually exclusive and exhaustive, as follows (see Figure 1):• Region within the alarm limits:
chart, one can divide the control area into three regions mutually exclusive and exhaustive, as follows (see Figure 1):• Region within the alarm limits: 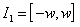 .• Region between the control and alarm limits:
.• Region between the control and alarm limits: 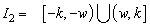 .• Region outside the control limits:
.• Region outside the control limits: 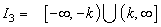 .
. | Figure 1. Control regions of a chart with variable sample size and interval |
If the statistic 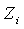 is marked within region
is marked within region 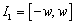 , the control (or inspection) is relaxed using the pair
, the control (or inspection) is relaxed using the pair 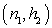 , otherwise, if the current point
, otherwise, if the current point 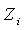 lies within region
lies within region 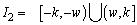 , control will be stricter using the pair
, control will be stricter using the pair 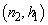 .
.
3. 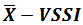 Chart Performance
Chart Performance
The statistical performance of a control chart can be evaluated by calculating the ARL or ATS statistics. Depending on the process operating condition, there is the ARL when the process is in control (ARL0), that is, the expected number of samples between two successive false alarms and the ARL for process out of control 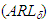 , which represents the expected number of samples between the occurrence of special cause that alters the monitored parameter and the signal triggered by the graph. The symbol
, which represents the expected number of samples between the occurrence of special cause that alters the monitored parameter and the signal triggered by the graph. The symbol 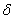 represents the displacement degree occurred in the process average and can be calculated by the expression:
represents the displacement degree occurred in the process average and can be calculated by the expression: 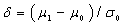 where
where 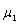 represents the new mean baseline after the process is out of adjustment [8]. Similarly, there is the ATS when the process is in control (ATS0), representing the average time between two successive false alarms and the ATS for process out of control
represents the new mean baseline after the process is out of adjustment [8]. Similarly, there is the ATS when the process is in control (ATS0), representing the average time between two successive false alarms and the ATS for process out of control 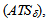 representing the expected time between the occurrence of special cause and the signal triggered by the graph.
representing the expected time between the occurrence of special cause and the signal triggered by the graph.
3.1. Markov Chains for 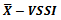 Chart
Chart
It is possible to calculate the ARL and ATS statistics using Markov chains. One observes the expected number of transitions before the monitored statistics to be in absorbing state of the chain. The Markov chain, proposed by Zimmer [11], was used in this article to evaluate the ARL in control and out of control, ARL0 and 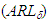 , respectively. Each transition probability is calculated as a probability of the statistics to be within one of the regions of the control range (
, respectively. Each transition probability is calculated as a probability of the statistics to be within one of the regions of the control range (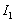 ,
,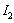 or
or 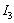 ). In this chain, there are two transient states and an absorbing state that corresponds to the process out of control.The matrix of transition of chain states which represents the operation of the process in control
). In this chain, there are two transient states and an absorbing state that corresponds to the process out of control.The matrix of transition of chain states which represents the operation of the process in control 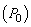 can be divided into four submatrices:
can be divided into four submatrices: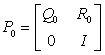 | (3) |
where  is the transition matrix between transient states;
is the transition matrix between transient states;  is the transition matrix of transient states to absorbing state;
is the transition matrix of transient states to absorbing state;  is the matrix that affirms the impossibility of going from an absorbing to a transient state and I is the identity matrix.In a Markov chain, the element (i,j) of the matrix
is the matrix that affirms the impossibility of going from an absorbing to a transient state and I is the identity matrix.In a Markov chain, the element (i,j) of the matrix 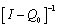 represents the average number of visits to the j transient state before reaching the absorbing state, since the process started in I state. Each transition probability in control is calculated as the probability of a point of the monitored statistic being situated within one of the regions of the control interval. Therefore,
represents the average number of visits to the j transient state before reaching the absorbing state, since the process started in I state. Each transition probability in control is calculated as the probability of a point of the monitored statistic being situated within one of the regions of the control interval. Therefore, 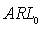 is calculated by:
is calculated by: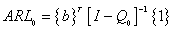 | (4) |
where 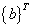 is a vector with initial probabilities; I is the identity matrix;
is a vector with initial probabilities; I is the identity matrix; 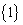 is a unit vector and
is a unit vector and 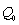 is a transition matrix.
is a transition matrix.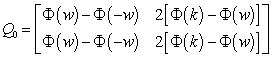 | (5) |
where 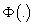 denotes the standard normal cumulative function; k and w are the limits that define the chart control region.The average time so that the chart produces a false alarm is:
denotes the standard normal cumulative function; k and w are the limits that define the chart control region.The average time so that the chart produces a false alarm is: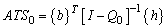 | (6) |
where 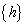 is a vector with the sampling intervals.The process transition matrix operating out of control is given by:
is a vector with the sampling intervals.The process transition matrix operating out of control is given by: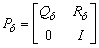 | (7) |
In order to calculate the measures of performance 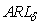 and
and 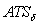 it is used:
it is used: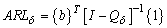 | (8) |
and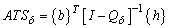 | (9) |
being the transition matrix given by: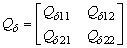 | (10) |
where: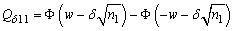 ;
;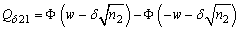 ;
;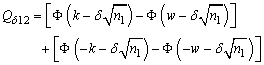 ;
;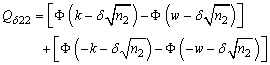 .The vector with initial probabilities
.The vector with initial probabilities 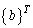 is defined according to the initial conditions of operation in the process:
is defined according to the initial conditions of operation in the process: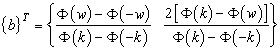 | (11) |
This article considers the condition known as Steady-State, that is, it is assumed that the process starts in control and, at some future time, there is a special question that causes a shift in the target value of the monitored statistics.
3.2. Optimum Statistical Design for the  Chart
Chart
The planning of a control chart can be formalized as an optimization problem in which the decision variables are the chart parameters. Figure 2 illustrates the objective function and constraints that define the optimal set of parameter of chart  .
. | Figure 2. Objective function and constraints for the control chart parameters 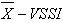 |
In Figure 2, 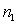 and
and 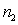 are the sample sizes;
are the sample sizes; 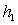 and
and 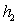 are the time intervals between sample collection; w and k are chart control limits;
are the time intervals between sample collection; w and k are chart control limits; 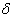 is the displacement degree occurred in the process mean;
is the displacement degree occurred in the process mean; 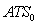 is the average time between two successive false alarms;
is the average time between two successive false alarms; 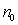 is the expected value of the sample size collected with the process in control;
is the expected value of the sample size collected with the process in control; 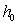 is the expected time to collect a sample with process in control and
is the expected time to collect a sample with process in control and 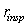 is the quantity of pieces (a part, a component, etc.) which can be inspected per time unit considered in
is the quantity of pieces (a part, a component, etc.) which can be inspected per time unit considered in 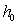 .To illustrate that the optimization problem is reduced to find the pair (n1,n2) that minimizes the objective function, consider, with no generality loss, that
.To illustrate that the optimization problem is reduced to find the pair (n1,n2) that minimizes the objective function, consider, with no generality loss, that 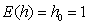 time unit (e.g. 1 hour, 0.5 hours, etc.) and ARL0=370.4. Therefore, ATS0=ARL0=370.4 and k=3. The expected value of the sample size with the process in control,
time unit (e.g. 1 hour, 0.5 hours, etc.) and ARL0=370.4. Therefore, ATS0=ARL0=370.4 and k=3. The expected value of the sample size with the process in control, 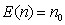 , is given by:
, is given by: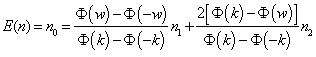 | (12) |
A pair of samples 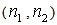 is selected; since
is selected; since 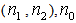 and k are known, w can be inferred directly from the expression (12).The shorter ideal sampling interval
and k are known, w can be inferred directly from the expression (12).The shorter ideal sampling interval 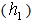 is:
is: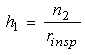 | (13) |
where 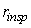 is the amount of parts (a part, component, etc.) which can be inspected per time unit considered in
is the amount of parts (a part, component, etc.) which can be inspected per time unit considered in 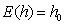 . For example, if
. For example, if 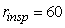 given that
given that 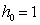 hour, it is assumed that it is possible to inspect 60 pieces every hour. For more details, see Celano [14, 15].Once defined h0, h1, w and k, one can obtain h2 through the expected time to collect a sample:
hour, it is assumed that it is possible to inspect 60 pieces every hour. For more details, see Celano [14, 15].Once defined h0, h1, w and k, one can obtain h2 through the expected time to collect a sample: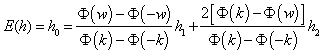 | (14) |
The optimization problem is finally reduced to find the pair 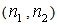 that minimizes the objective function.Section 4 presents an application example in which one reveals values that the pair
that minimizes the objective function.Section 4 presents an application example in which one reveals values that the pair 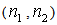 should be used. For this, one used the software R [18] as a tool to calculate the optimal parameters of an
should be used. For this, one used the software R [18] as a tool to calculate the optimal parameters of an 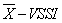 chart.
chart.
4. Example
In this section, one proposes two functions (see Appendix) developed for use in the R software that evaluate the 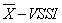 control chart performance and solve the optimization problem shown in Figure 2.The first function, called VSSI, evaluates the control chart performance by calculating the ATSwhen provided by the user: n1, n2, n, delta
control chart performance and solve the optimization problem shown in Figure 2.The first function, called VSSI, evaluates the control chart performance by calculating the ATSwhen provided by the user: n1, n2, n, delta 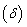 , h0 and r_insp.The second function, VSSI.optimum, solves the optimization problem shown in Figure 2. This function requires as input: n0, delta
, h0 and r_insp.The second function, VSSI.optimum, solves the optimization problem shown in Figure 2. This function requires as input: n0, delta 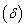 , h0, r_insp and a value for nmax that refers to the highest size of sample allowable for collection.To illustrate the use of functions, consider the example shown in Costa [8]. A packaging milk line has an average value of 1000 mL and a standard deviation estimated to be 4.32 mL. It is done the monitoring of the average of the process by inspecting samples size n0 = 5 at every time unit. Suppose that such a unit is equal to h0=60 minutes. In this example, the parameters designed for the control chart are fixed, that is, the sample size, the sampling interval and the limits do not alter after they are estimated. In order to use the
, h0, r_insp and a value for nmax that refers to the highest size of sample allowable for collection.To illustrate the use of functions, consider the example shown in Costa [8]. A packaging milk line has an average value of 1000 mL and a standard deviation estimated to be 4.32 mL. It is done the monitoring of the average of the process by inspecting samples size n0 = 5 at every time unit. Suppose that such a unit is equal to h0=60 minutes. In this example, the parameters designed for the control chart are fixed, that is, the sample size, the sampling interval and the limits do not alter after they are estimated. In order to use the 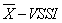 control chart, it is necessary to calculate the control limits (w and k) and the sampling scheme
control chart, it is necessary to calculate the control limits (w and k) and the sampling scheme 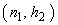 and
and 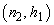 . Selecting, for instance,
. Selecting, for instance, 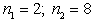 ;
; 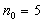 ;
; 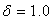 ; ARL0=370.3983; h0=60 and r_insp=60, the VSSI function provides the parameters shown in Figure 3.
; ARL0=370.3983; h0=60 and r_insp=60, the VSSI function provides the parameters shown in Figure 3. | Figure 3. Parameters obtained with the function VSSI (n1=2, n2=8, n0_FSR=5, delta=1, ARL0=370.3983, h0=60, r_insp=60). Note: h0should be set in minutes |
In this example, 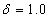 means that the process average went from
means that the process average went from 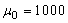 (in control) to
(in control) to 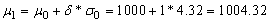 (out of control).Consider the case where
(out of control).Consider the case where 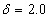 . The Figure 4 illustrates the results obtained with the function VSSI. It is observed that the ATS is lower
. The Figure 4 illustrates the results obtained with the function VSSI. It is observed that the ATS is lower 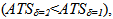 then, when major deviations occur in the process mean, the chart performance is better.
then, when major deviations occur in the process mean, the chart performance is better. | Figure 4. Parameters obtained with function VSSI (n1=2, n2=8, n0_FSR=5, delta=2, ARL0=370.3983, h0=60, r_insp=60) |
However, an optimum scheme to monitor this process is the one presenting the best performance, that is, the lowest 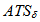 . By means of VSSI. optimum function, one can obtain parameters that minimize
. By means of VSSI. optimum function, one can obtain parameters that minimize 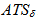 . Figure 5 shows the best schemes for the cases shown in Figures 3 and 4.
. Figure 5 shows the best schemes for the cases shown in Figures 3 and 4. | Figure 5. Parameters obtained with the function VSSI.optimum (n0_FSR, delta, ARL0, h0, r_insp, nmax) |
In this case, the user who wants to control the average value of a process considering a displacement possibility presented here, has simply to build the 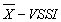 control chart with the parameters shown in Figure 5. Other
control chart with the parameters shown in Figure 5. Other 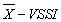 charts can be easily constructed by modifying input values of functions VSSI and VSSI.optimum.
charts can be easily constructed by modifying input values of functions VSSI and VSSI.optimum.
5. Conclusions
It was displayed in this article, how it evaluates the control chart performance of 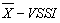 by means of Markov chains and, mainly, how to get the parameters that minimize the ATS. For this, two functions written in the language setting to R were created in order to minimize the ATS and present the best parameters to be used in constructing the
by means of Markov chains and, mainly, how to get the parameters that minimize the ATS. For this, two functions written in the language setting to R were created in order to minimize the ATS and present the best parameters to be used in constructing the 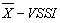 control chart. Adaptive schemes are recognized as being more efficient than the control charts schemes with fixed parameters. Nevertheless, the use of adaptive schemes for control graphs is not common in practice, because the traditional statistical software do not display routines for these types of charts. Thus, with the programs presented here, the user has a tool in which it is possible to plan the
control chart. Adaptive schemes are recognized as being more efficient than the control charts schemes with fixed parameters. Nevertheless, the use of adaptive schemes for control graphs is not common in practice, because the traditional statistical software do not display routines for these types of charts. Thus, with the programs presented here, the user has a tool in which it is possible to plan the 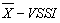 control chart use in order to monitor the average value of a feature of desired quality.
control chart use in order to monitor the average value of a feature of desired quality.
Appendix
Source code to evaluate the performance and choose an optimum statistical design for the control chart 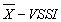 in R environment.It is presented hereafter two functions called VSSI and VSSI.optimum. To use them, simply copy them in the R environment and follow the application example.
in R environment.It is presented hereafter two functions called VSSI and VSSI.optimum. To use them, simply copy them in the R environment and follow the application example. Source code to evaluate the performance and choose an optimum statistical design for the control chart
Source code to evaluate the performance and choose an optimum statistical design for the control chart 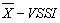 in R environment (Continuation).
in R environment (Continuation).
References
| [1] | W.A. Shewhart, Economic control of quality of manufactured product. 1ª Ed. NewYork: D. Van Nostrand Company, 1931. |
| [2] | M. R. Jr. Reynolds, J.C. Arnold, J.A. Nachlas,  charts with variable sampling intervals, Technometrics, 30, 181-192, 1988. charts with variable sampling intervals, Technometrics, 30, 181-192, 1988. |
| [3] | S.S. Prabhu, D.C. Montgomery, G.C. Runger, A combined adaptive sample size and sampling interval  control scheme, Journal of Quality Technology, 26, 164-176, 1994. control scheme, Journal of Quality Technology, 26, 164-176, 1994. |
| [4] | S.S. Prabhu, D.C. Montgomery, G.C. Runger, Economic- statistical design of an adaptive  chart, International Journal of Production Economics, 49, 1-15, 1997. chart, International Journal of Production Economics, 49, 1-15, 1997. |
| [5] | A.F.B. Costa, 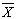 charts with variable sample size, Journal of Quality Technology, 26, 155-163, 1994. charts with variable sample size, Journal of Quality Technology, 26, 155-163, 1994. |
| [6] | A.F.B. Costa, 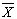 charts with variable sample size and sampling intervals, Journal of Quality Technology, 29, 197-204, 1997. charts with variable sample size and sampling intervals, Journal of Quality Technology, 29, 197-204, 1997. |
| [7] | A.F.B. Costa, 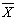 charts with variable parameters, Journal of Quality Technology, 31, 408-416, 1999. charts with variable parameters, Journal of Quality Technology, 31, 408-416, 1999. |
| [8] | A.F.B. Costa, E.K. Epprecht, L.C.R. Carpinetti,Controle Estatístico de Qualidade,São Paulo, Atlas, 2008. |
| [9] | C. Park, M.R. Jr. Reynolds, Economic design of a variable sample size X chart, Communications in statistics – simulation and computation, 23, 467- 483, 1994. |
| [10] | C. Park, M.R. Jr. Reynolds, Economic design of a variable sampling rate 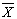 chart, Journal of Quality Technology, 31, 427-443, 1999. chart, Journal of Quality Technology, 31, 427-443, 1999. |
| [11] | L.S. Zimmer, D.C. Montgomery, G.C. Runger, Guidelines for the application of adaptive control charting schemes, International Journal of Production Research, 38(9), 1977-1992, 2000. |
| [12] | A. Faraz, E. Saniga, A unification and some corrections to Markov chain approaches to develop variable ratio sampling scheme control charts, Statistical Papers, 52(4), 799-811, 2011. |
| [13] | R.C. Leoni, A.F.B. Costa, O ambiente R como proposta de apoio ao ensino no monitoramento de processos, Pesquisa Operacional para o Desenvolvimento, 4(1), 83-96, 2012. |
| [14] | M.S. Magalhães, E.K. Epprecht, A.F.B. Costa, Economic design of a Vp 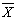 chart, International Journal of Production Economics, 74, 191-200, 2001. chart, International Journal of Production Economics, 74, 191-200, 2001. |
| [15] | D.S. Bai, K. T. Lee, An economic design of variable sampling interval control chart, International journal of production economics, 54, 57- 64, 1998. |
| [16] | G. Celano, Robust design of adaptive control charts for manual manufacturing/inspection workstations, Journal of Applied Statistics, 36(2), 181-203, 2009. |
| [17] | G. Celano, On the constrained economic design of control charts: a literature review, Produção, 21(2), 223-234, 2011. |
| [18] | R Development Core Team (2011). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org/. |
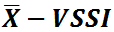 Control Chart with Adaptive Parameters
Control Chart with Adaptive Parameters
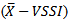 variable sample size and interval. The
variable sample size and interval. The 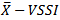 chart was chosen because it is a scheme with great potential for practical application and only requires knowledge of the sample size and the time between sample selection. Markov chains were used to evaluate the chart performance based on the average time between the process uncontrolled and the signal generated by the chart. Two functions written in R language that assist the user in the design of an adaptive control chart
chart was chosen because it is a scheme with great potential for practical application and only requires knowledge of the sample size and the time between sample selection. Markov chains were used to evaluate the chart performance based on the average time between the process uncontrolled and the signal generated by the chart. Two functions written in R language that assist the user in the design of an adaptive control chart 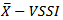 are exhibited.
are exhibited.
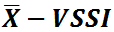 Control Chart with Adaptive Parameters, American Journal of Mathematics and Statistics, Vol. 5 No. 5, 2015, pp. 285-292. doi: 10.5923/j.ajms.20150505.09.
Control Chart with Adaptive Parameters, American Journal of Mathematics and Statistics, Vol. 5 No. 5, 2015, pp. 285-292. doi: 10.5923/j.ajms.20150505.09.
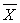 with sample size and interval being variable (
with sample size and interval being variable (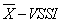 ). The average number of samples until the moment in which the chart indicates the out of control condition (ARL) and the average time between the instant in which the process is changed and the time in which the graph indicates the out of control condition (ATS) are the performance measures used as a reference for the parameters choice. The ARL (Average Run Length) is the average number of points that must be plotted before a point indicates an out-of-control condition, the ATS (Average Time to Signal) represents the average time needed for the control scheme to detect a situation outside of control from the beginning of the process.The
). The average number of samples until the moment in which the chart indicates the out of control condition (ARL) and the average time between the instant in which the process is changed and the time in which the graph indicates the out of control condition (ATS) are the performance measures used as a reference for the parameters choice. The ARL (Average Run Length) is the average number of points that must be plotted before a point indicates an out-of-control condition, the ATS (Average Time to Signal) represents the average time needed for the control scheme to detect a situation outside of control from the beginning of the process.The 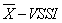 chart was chosen because it is a scheme with great potential for practical application, for its use requires only to know the sample size and the time between samples selection after the optimal parameters are established. The statistical properties of control chart are optimized considering the approach presented by Zimmer [11], that is, a Markov chain is used to establish the parameters keeping under control the statistical risk type I and type II [12].The rest of the paper is organized as follows: section 2 presents the
chart was chosen because it is a scheme with great potential for practical application, for its use requires only to know the sample size and the time between samples selection after the optimal parameters are established. The statistical properties of control chart are optimized considering the approach presented by Zimmer [11], that is, a Markov chain is used to establish the parameters keeping under control the statistical risk type I and type II [12].The rest of the paper is organized as follows: section 2 presents the 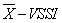 control chart. In section 3, it is described the procedure to evaluate the performance of a
control chart. In section 3, it is described the procedure to evaluate the performance of a 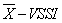 chart using Markov chains. In Section 4, two functions written in R language that assist the user in the design of an adaptive control chart
chart using Markov chains. In Section 4, two functions written in R language that assist the user in the design of an adaptive control chart 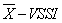 are exhibited. Finally, conclusions and future research directions complete the article.Two functions written in R language that assist the user in the design of an adaptive control chart
are exhibited. Finally, conclusions and future research directions complete the article.Two functions written in R language that assist the user in the design of an adaptive control chart 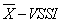 are exhibited.
are exhibited.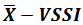 Control Chart
Control Chart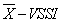 control chart is adaptive with respect to the sample size and the time interval in which a sample is collected. This chart was used by several researchers [3, 4, 9, 10] for monitoring the
control chart is adaptive with respect to the sample size and the time interval in which a sample is collected. This chart was used by several researchers [3, 4, 9, 10] for monitoring the 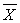 statistics of a process.In a control chart with sample size and interval being variable (see Figure 1) the sample size and time interval in which a sample is taken can vary depending on the information from the most recent sample collected. In this kind of chart, random samples of different sizes are collected in intervals of variable length according to the function:
statistics of a process.In a control chart with sample size and interval being variable (see Figure 1) the sample size and time interval in which a sample is taken can vary depending on the information from the most recent sample collected. In this kind of chart, random samples of different sizes are collected in intervals of variable length according to the function: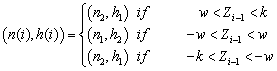
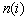 is the size of the ith sample
is the size of the ith sample 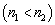 ;
; 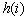 is the time practiced to remove the ith sample
is the time practiced to remove the ith sample 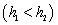 ; k and w are boundaries that define control regions;
; k and w are boundaries that define control regions; 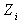 is the control statistics.
is the control statistics.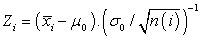
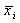 is the sample average of the i-th subgroup;
is the sample average of the i-th subgroup; 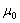 and
and 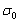 are the mean and standard deviation of the process when in control.The choice between the pairs
are the mean and standard deviation of the process when in control.The choice between the pairs 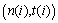 depends on the position of the last point
depends on the position of the last point 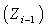 marked on the chart. For a
marked on the chart. For a 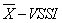 chart, one can divide the control area into three regions mutually exclusive and exhaustive, as follows (see Figure 1):• Region within the alarm limits:
chart, one can divide the control area into three regions mutually exclusive and exhaustive, as follows (see Figure 1):• Region within the alarm limits: 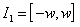 .• Region between the control and alarm limits:
.• Region between the control and alarm limits: 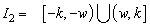 .• Region outside the control limits:
.• Region outside the control limits: 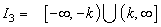 .
.
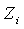 is marked within region
is marked within region 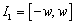 , the control (or inspection) is relaxed using the pair
, the control (or inspection) is relaxed using the pair 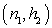 , otherwise, if the current point
, otherwise, if the current point 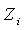 lies within region
lies within region 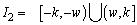 , control will be stricter using the pair
, control will be stricter using the pair 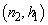 .
.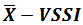 Chart Performance
Chart Performance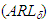 , which represents the expected number of samples between the occurrence of special cause that alters the monitored parameter and the signal triggered by the graph. The symbol
, which represents the expected number of samples between the occurrence of special cause that alters the monitored parameter and the signal triggered by the graph. The symbol 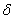 represents the displacement degree occurred in the process average and can be calculated by the expression:
represents the displacement degree occurred in the process average and can be calculated by the expression: 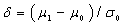 where
where 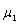 represents the new mean baseline after the process is out of adjustment [8]. Similarly, there is the ATS when the process is in control (ATS0), representing the average time between two successive false alarms and the ATS for process out of control
represents the new mean baseline after the process is out of adjustment [8]. Similarly, there is the ATS when the process is in control (ATS0), representing the average time between two successive false alarms and the ATS for process out of control 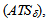 representing the expected time between the occurrence of special cause and the signal triggered by the graph.
representing the expected time between the occurrence of special cause and the signal triggered by the graph.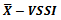 Chart
Chart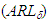 , respectively. Each transition probability is calculated as a probability of the statistics to be within one of the regions of the control range (
, respectively. Each transition probability is calculated as a probability of the statistics to be within one of the regions of the control range (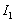 ,
,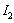 or
or 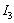 ). In this chain, there are two transient states and an absorbing state that corresponds to the process out of control.The matrix of transition of chain states which represents the operation of the process in control
). In this chain, there are two transient states and an absorbing state that corresponds to the process out of control.The matrix of transition of chain states which represents the operation of the process in control 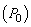 can be divided into four submatrices:
can be divided into four submatrices: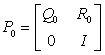
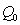 is the transition matrix between transient states;
is the transition matrix between transient states; 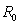 is the transition matrix of transient states to absorbing state;
is the transition matrix of transient states to absorbing state; 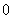 is the matrix that affirms the impossibility of going from an absorbing to a transient state and I is the identity matrix.In a Markov chain, the element (i,j) of the matrix
is the matrix that affirms the impossibility of going from an absorbing to a transient state and I is the identity matrix.In a Markov chain, the element (i,j) of the matrix 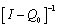 represents the average number of visits to the j transient state before reaching the absorbing state, since the process started in I state. Each transition probability in control is calculated as the probability of a point of the monitored statistic being situated within one of the regions of the control interval. Therefore,
represents the average number of visits to the j transient state before reaching the absorbing state, since the process started in I state. Each transition probability in control is calculated as the probability of a point of the monitored statistic being situated within one of the regions of the control interval. Therefore, 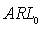 is calculated by:
is calculated by: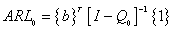
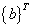 is a vector with initial probabilities; I is the identity matrix;
is a vector with initial probabilities; I is the identity matrix; 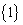 is a unit vector and
is a unit vector and 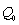 is a transition matrix.
is a transition matrix.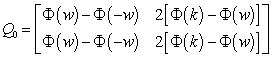
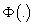 denotes the standard normal cumulative function; k and w are the limits that define the chart control region.The average time so that the chart produces a false alarm is:
denotes the standard normal cumulative function; k and w are the limits that define the chart control region.The average time so that the chart produces a false alarm is: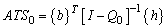
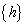 is a vector with the sampling intervals.The process transition matrix operating out of control is given by:
is a vector with the sampling intervals.The process transition matrix operating out of control is given by: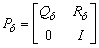
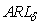 and
and 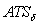 it is used:
it is used: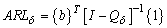
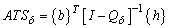
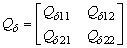
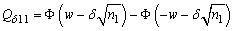 ;
;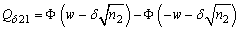 ;
;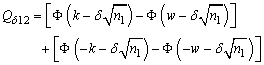 ;
;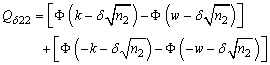 .The vector with initial probabilities
.The vector with initial probabilities 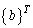 is defined according to the initial conditions of operation in the process:
is defined according to the initial conditions of operation in the process: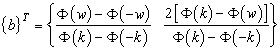
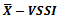 Chart
Chart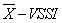 .
.
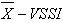
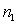 and
and 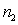 are the sample sizes;
are the sample sizes; 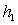 and
and 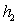 are the time intervals between sample collection; w and k are chart control limits;
are the time intervals between sample collection; w and k are chart control limits; 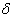 is the displacement degree occurred in the process mean;
is the displacement degree occurred in the process mean; 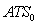 is the average time between two successive false alarms;
is the average time between two successive false alarms; 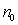 is the expected value of the sample size collected with the process in control;
is the expected value of the sample size collected with the process in control; 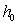 is the expected time to collect a sample with process in control and
is the expected time to collect a sample with process in control and 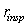 is the quantity of pieces (a part, a component, etc.) which can be inspected per time unit considered in
is the quantity of pieces (a part, a component, etc.) which can be inspected per time unit considered in 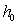 .To illustrate that the optimization problem is reduced to find the pair (n1,n2) that minimizes the objective function, consider, with no generality loss, that
.To illustrate that the optimization problem is reduced to find the pair (n1,n2) that minimizes the objective function, consider, with no generality loss, that 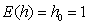 time unit (e.g. 1 hour, 0.5 hours, etc.) and ARL0=370.4. Therefore, ATS0=ARL0=370.4 and k=3. The expected value of the sample size with the process in control,
time unit (e.g. 1 hour, 0.5 hours, etc.) and ARL0=370.4. Therefore, ATS0=ARL0=370.4 and k=3. The expected value of the sample size with the process in control, 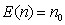 , is given by:
, is given by: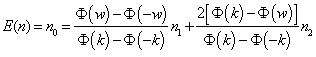
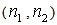 is selected; since
is selected; since 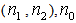 and k are known, w can be inferred directly from the expression (12).The shorter ideal sampling interval
and k are known, w can be inferred directly from the expression (12).The shorter ideal sampling interval 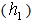 is:
is: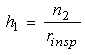
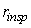 is the amount of parts (a part, component, etc.) which can be inspected per time unit considered in
is the amount of parts (a part, component, etc.) which can be inspected per time unit considered in 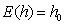 . For example, if
. For example, if 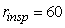 given that
given that 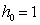 hour, it is assumed that it is possible to inspect 60 pieces every hour. For more details, see Celano [14, 15].Once defined h0, h1, w and k, one can obtain h2 through the expected time to collect a sample:
hour, it is assumed that it is possible to inspect 60 pieces every hour. For more details, see Celano [14, 15].Once defined h0, h1, w and k, one can obtain h2 through the expected time to collect a sample: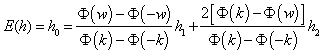
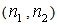 that minimizes the objective function.Section 4 presents an application example in which one reveals values that the pair
that minimizes the objective function.Section 4 presents an application example in which one reveals values that the pair 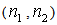 should be used. For this, one used the software R [18] as a tool to calculate the optimal parameters of an
should be used. For this, one used the software R [18] as a tool to calculate the optimal parameters of an 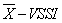 chart.
chart.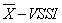 control chart performance and solve the optimization problem shown in Figure 2.The first function, called VSSI, evaluates the control chart performance by calculating the ATSwhen provided by the user: n1, n2, n, delta
control chart performance and solve the optimization problem shown in Figure 2.The first function, called VSSI, evaluates the control chart performance by calculating the ATSwhen provided by the user: n1, n2, n, delta 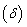 , h0 and r_insp.The second function, VSSI.optimum, solves the optimization problem shown in Figure 2. This function requires as input: n0, delta
, h0 and r_insp.The second function, VSSI.optimum, solves the optimization problem shown in Figure 2. This function requires as input: n0, delta 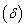 , h0, r_insp and a value for nmax that refers to the highest size of sample allowable for collection.To illustrate the use of functions, consider the example shown in Costa [8]. A packaging milk line has an average value of 1000 mL and a standard deviation estimated to be 4.32 mL. It is done the monitoring of the average of the process by inspecting samples size n0 = 5 at every time unit. Suppose that such a unit is equal to h0=60 minutes. In this example, the parameters designed for the control chart are fixed, that is, the sample size, the sampling interval and the limits do not alter after they are estimated. In order to use the
, h0, r_insp and a value for nmax that refers to the highest size of sample allowable for collection.To illustrate the use of functions, consider the example shown in Costa [8]. A packaging milk line has an average value of 1000 mL and a standard deviation estimated to be 4.32 mL. It is done the monitoring of the average of the process by inspecting samples size n0 = 5 at every time unit. Suppose that such a unit is equal to h0=60 minutes. In this example, the parameters designed for the control chart are fixed, that is, the sample size, the sampling interval and the limits do not alter after they are estimated. In order to use the 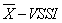 control chart, it is necessary to calculate the control limits (w and k) and the sampling scheme
control chart, it is necessary to calculate the control limits (w and k) and the sampling scheme 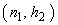 and
and 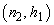 . Selecting, for instance,
. Selecting, for instance, 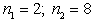 ;
; 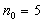 ;
; 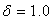 ; ARL0=370.3983; h0=60 and r_insp=60, the VSSI function provides the parameters shown in Figure 3.
; ARL0=370.3983; h0=60 and r_insp=60, the VSSI function provides the parameters shown in Figure 3.
 means that the process average went from
means that the process average went from 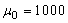 (in control) to
(in control) to 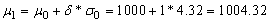 (out of control).Consider the case where
(out of control).Consider the case where 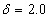 . The Figure 4 illustrates the results obtained with the function VSSI. It is observed that the ATS is lower
. The Figure 4 illustrates the results obtained with the function VSSI. It is observed that the ATS is lower 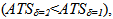 then, when major deviations occur in the process mean, the chart performance is better.
then, when major deviations occur in the process mean, the chart performance is better.
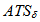 . By means of VSSI. optimum function, one can obtain parameters that minimize
. By means of VSSI. optimum function, one can obtain parameters that minimize 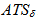 . Figure 5 shows the best schemes for the cases shown in Figures 3 and 4.
. Figure 5 shows the best schemes for the cases shown in Figures 3 and 4.
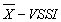 control chart with the parameters shown in Figure 5. Other
control chart with the parameters shown in Figure 5. Other 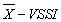 charts can be easily constructed by modifying input values of functions VSSI and VSSI.optimum.
charts can be easily constructed by modifying input values of functions VSSI and VSSI.optimum. 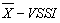 by means of Markov chains and, mainly, how to get the parameters that minimize the ATS. For this, two functions written in the language setting to R were created in order to minimize the ATS and present the best parameters to be used in constructing the
by means of Markov chains and, mainly, how to get the parameters that minimize the ATS. For this, two functions written in the language setting to R were created in order to minimize the ATS and present the best parameters to be used in constructing the 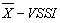 control chart. Adaptive schemes are recognized as being more efficient than the control charts schemes with fixed parameters. Nevertheless, the use of adaptive schemes for control graphs is not common in practice, because the traditional statistical software do not display routines for these types of charts. Thus, with the programs presented here, the user has a tool in which it is possible to plan the
control chart. Adaptive schemes are recognized as being more efficient than the control charts schemes with fixed parameters. Nevertheless, the use of adaptive schemes for control graphs is not common in practice, because the traditional statistical software do not display routines for these types of charts. Thus, with the programs presented here, the user has a tool in which it is possible to plan the 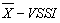 control chart use in order to monitor the average value of a feature of desired quality.
control chart use in order to monitor the average value of a feature of desired quality.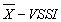 in R environment.It is presented hereafter two functions called VSSI and VSSI.optimum. To use them, simply copy them in the R environment and follow the application example.
in R environment.It is presented hereafter two functions called VSSI and VSSI.optimum. To use them, simply copy them in the R environment and follow the application example. Source code to evaluate the performance and choose an optimum statistical design for the control chart
Source code to evaluate the performance and choose an optimum statistical design for the control chart 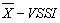 in R environment (Continuation).
in R environment (Continuation).
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML charts with variable sampling intervals, Technometrics, 30, 181-192, 1988.
charts with variable sampling intervals, Technometrics, 30, 181-192, 1988.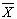 control scheme, Journal of Quality Technology, 26, 164-176, 1994.
control scheme, Journal of Quality Technology, 26, 164-176, 1994.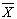 chart, International Journal of Production Economics, 49, 1-15, 1997.
chart, International Journal of Production Economics, 49, 1-15, 1997.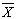 charts with variable sample size, Journal of Quality Technology, 26, 155-163, 1994.
charts with variable sample size, Journal of Quality Technology, 26, 155-163, 1994.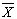 charts with variable sample size and sampling intervals, Journal of Quality Technology, 29, 197-204, 1997.
charts with variable sample size and sampling intervals, Journal of Quality Technology, 29, 197-204, 1997.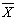 charts with variable parameters, Journal of Quality Technology, 31, 408-416, 1999.
charts with variable parameters, Journal of Quality Technology, 31, 408-416, 1999.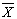 chart, Journal of Quality Technology, 31, 427-443, 1999.
chart, Journal of Quality Technology, 31, 427-443, 1999. chart, International Journal of Production Economics, 74, 191-200, 2001.
chart, International Journal of Production Economics, 74, 191-200, 2001.